exponent?
+
+# --hints--
+
+`powerDigitSum(15)` should return a number.
+
+```js
+assert(typeof powerDigitSum(15) === 'number');
+```
+
+`powerDigitSum(15)` should return 26.
+
+```js
+assert.strictEqual(powerDigitSum(15), 26);
+```
+
+`powerDigitSum(128)` should return 166.
+
+```js
+assert.strictEqual(powerDigitSum(128), 166);
+```
+
+`powerDigitSum(1000)` should return 1366.
+
+```js
+assert.strictEqual(powerDigitSum(1000), 1366);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function powerDigitSum(exponent) {
+
+ return true;
+}
+
+powerDigitSum(15);
+```
+
+# --solutions--
+
+```js
+function powerDigitSum(exponent) {
+ const bigNum = [1];
+ let sum = 0;
+
+ for (let i = 1; i <= exponent; i++) {
+ let count = bigNum.length + 1;
+ let overflow = 0;
+ for (let j = 0; j < count; j++) {
+ let digit = bigNum[j] || 0;
+ digit = 2 * digit + overflow;
+
+ if (digit > 9) {
+ digit -= 10;
+ overflow = 1;
+ } else {
+ overflow = 0;
+ }
+
+ bigNum[j] = digit;
+ }
+ }
+
+ bigNum.forEach(function(num) {
+ return sum += num;
+ });
+
+ return sum;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-17-number-letter-counts.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-17-number-letter-counts.md
new file mode 100644
index 00000000000..c64e9f073f6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-17-number-letter-counts.md
@@ -0,0 +1,130 @@
+---
+id: 5900f37d1000cf542c50fe90
+title: 'Problem 17: Number letter counts'
+challengeType: 1
+forumTopicId: 301804
+dashedName: problem-17-number-letter-counts
+---
+
+# --description--
+
+If the numbers 1 to 5 are written out in words: one, two, three, four, five, then there are 3 + 3 + 5 + 4 + 4 = 19 letters used in total.
+
+If all the numbers from 1 to given `limit` inclusive were written out in words, how many letters would be used?
+
+**Note:** Do not count spaces or hyphens. For example, 342 (three hundred and forty-two) contains 23 letters and 115 (one hundred and fifteen) contains 20 letters. The use of "and" when writing out numbers is in compliance with British usage.
+
+# --hints--
+
+`numberLetterCounts(5)` should return a number.
+
+```js
+assert(typeof numberLetterCounts(5) === 'number');
+```
+
+`numberLetterCounts(5)` should return 19.
+
+```js
+assert.strictEqual(numberLetterCounts(5), 19);
+```
+
+`numberLetterCounts(150)` should return 1903.
+
+```js
+assert.strictEqual(numberLetterCounts(150), 1903);
+```
+
+`numberLetterCounts(1000)` should return 21124.
+
+```js
+assert.strictEqual(numberLetterCounts(1000), 21124);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function numberLetterCounts(limit) {
+
+ return true;
+}
+
+numberLetterCounts(5);
+```
+
+# --solutions--
+
+```js
+function numberLetterCounts(limit) {
+ const dictionary = {
+ 0: '',
+ 1: 'one',
+ 2: 'two',
+ 3: 'three',
+ 4: 'four',
+ 5: 'five',
+ 6: 'six',
+ 7: 'seven',
+ 8: 'eight',
+ 9: 'nine',
+ 10: 'ten',
+ 11: 'eleven',
+ 12: 'twelve',
+ 13: 'thirteen',
+ 14: 'fourteen',
+ 15: 'fifteen',
+ 16: 'sixteen',
+ 17: 'seventeen',
+ 18: 'eighteen',
+ 19: 'nineteen',
+ 20: 'twenty',
+ 30: 'thirty',
+ 40: 'forty',
+ 50: 'fifty',
+ 60: 'sixty',
+ 70: 'seventy',
+ 80: 'eighty',
+ 90: 'ninety',
+ 1000: 'onethousand'
+ };
+
+ let numString = '';
+
+ function convertToString(num) {
+ // check dictionary for number
+ if (dictionary[num]) {
+ return dictionary[num];
+ } else {
+ const hundreds = Math.floor(num / 100);
+ const tens = Math.floor((num / 10) % 10) * 10;
+ const remainder = num % 10;
+
+ let tempStr = '';
+
+ if (hundreds === 0) {
+ tempStr += dictionary[tens] + dictionary[remainder];
+ } else {
+ tempStr += dictionary[hundreds] + 'hundred';
+
+ if (tens !== 0 || remainder !== 0) {
+ tempStr += 'and';
+ }
+
+ if (tens < 20) {
+ const lessThanTwenty = tens + remainder;
+ tempStr += dictionary[lessThanTwenty];
+ } else {
+ tempStr += dictionary[tens] + dictionary[remainder];
+ }
+ }
+ return tempStr;
+ }
+ }
+
+ for (let i = 1; i <= limit; i++) {
+ numString += convertToString(i);
+ }
+ return numString.length;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-18-maximum-path-sum-i.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-18-maximum-path-sum-i.md
new file mode 100644
index 00000000000..f0d97a950b2
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-18-maximum-path-sum-i.md
@@ -0,0 +1,109 @@
+---
+id: 5900f37e1000cf542c50fe91
+title: 'Problem 18: Maximum path sum I'
+challengeType: 1
+forumTopicId: 301815
+dashedName: problem-18-maximum-path-sum-i
+---
+
+# --description--
+
+By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.
+
+
+ 3+ 7 4
+ 2 4 6
+ 8 5 9 3 + + +That is, 3 + 7 + 4 + 9 = 23. + +Find the maximum total from top to bottom of the triangle below: + +75 +95 64 +17 47 82 +18 35 87 10 +20 04 82 47 65 +19 01 23 75 03 34 +88 02 77 73 07 63 67 +99 65 04 28 06 16 70 92 +41 41 26 56 83 40 80 70 33 +41 48 72 33 47 32 37 16 94 29 +53 71 44 65 25 43 91 52 97 51 14 +70 11 33 28 77 73 17 78 39 68 17 57 +91 71 52 38 17 14 91 43 58 50 27 29 48 +63 66 04 68 89 53 67 30 73 16 69 87 40 31 +04 62 98 27 23 09 70 98 73 93 38 53 60 04 23 + +**NOTE:** As there are only 16384 routes, it is possible to solve this problem by trying every route. However, Problem 67, is the same challenge with a triangle containing one-hundred rows; it cannot be solved by brute force, and requires a clever method! ;o) + +# --hints-- + +`maximumPathSumI(testTriangle)` should return a number. + +```js +assert(typeof maximumPathSumI(testTriangle) === 'number'); +``` + +`maximumPathSumI(testTriangle)` should return 23. + +```js +assert.strictEqual(maximumPathSumI(testTriangle), 23); +``` + +`maximumPathSumI(numTriangle)` should return 1074. + +```js +assert.strictEqual(maximumPathSumI(numTriangle), 1074); +``` + +# --seed-- + +## --before-user-code-- + +```js +const numTriangle = [[75, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [95, 64, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [17, 47, 82, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [18, 35, 87, 10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [20, 4, 82, 47, 65, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [19, 1, 23, 75, 3, 34, 0, 0, 0, 0, 0, 0, 0, 0, 0], [88, 2, 77, 73, 7, 63, 67, 0, 0, 0, 0, 0, 0, 0, 0], [99, 65, 4, 28, 6, 16, 70, 92, 0, 0, 0, 0, 0, 0, 0], [41, 41, 26, 56, 83, 40, 80, 70, 33, 0, 0, 0, 0, 0, 0], [41, 48, 72, 33, 47, 32, 37, 16, 94, 29, 0, 0, 0, 0, 0], [53, 71, 44, 65, 25, 43, 91, 52, 97, 51, 14, 0, 0, 0, 0], [70, 11, 33, 28, 77, 73, 17, 78, 39, 68, 17, 57, 0, 0, 0], [91, 71, 52, 38, 17, 14, 91, 43, 58, 50, 27, 29, 48, 0, 0], [63, 66, 4, 68, 89, 53, 67, 30, 73, 16, 69, 87, 40, 31, 0], [4, 62, 98, 27, 23, 9, 70, 98, 73, 93, 38, 53, 60, 4, 23]]; +``` + +## --seed-contents-- + +```js +function maximumPathSumI(triangle) { + + return true; +} + +const testTriangle = [[3, 0, 0, 0], + [7, 4, 0, 0], + [2, 4, 6, 0], + [8, 5, 9, 3]]; + +maximumPathSumI(testTriangle); +``` + +# --solutions-- + +```js +const testTriangle = [[3, 0, 0, 0], + [7, 4, 0, 0], + [2, 4, 6, 0], + [8, 5, 9, 3]]; + +function maximumPathSumI(triangle) { + let maxSum = triangle.slice(); + + for (let i = triangle.length - 1; i > 0; i--) { + let currentRow = maxSum[i]; + let previousRow = maxSum[i - 1]; + const temp = []; + for (let j = 0; j < i; j++) { + temp.push(Math.max((currentRow[j] + previousRow[j]), (currentRow[j + 1] + previousRow[j]))); + } + maxSum[i - 1] = temp; + maxSum.pop(); + } + return maxSum[0][0]; +} +``` diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-19-counting-sundays.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-19-counting-sundays.md new file mode 100644 index 00000000000..5a3e24cc431 --- /dev/null +++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-19-counting-sundays.md @@ -0,0 +1,76 @@ +--- +id: 5900f37f1000cf542c50fe92 +title: 'Problem 19: Counting Sundays' +challengeType: 1 +forumTopicId: 301827 +dashedName: problem-19-counting-sundays +--- + +# --description-- + +You are given the following information, but you may prefer to do some research for yourself. + +
-
+
- 1 Jan 1900 was a Monday. +
- Thirty days has September,
April, June and November.
All the rest have thirty-one,
Saving February alone,
Which has twenty-eight, rain or shine.
And on leap years, twenty-nine.
+ - A leap year occurs on any year evenly divisible by 4, but not on a century unless it is divisible by 400. +
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
+
+By considering the terms in the Fibonacci sequence whose values do not exceed `n`, find the sum of the even-valued terms.
+
+# --hints--
+
+`fiboEvenSum(10)` should return a number.
+
+```js
+assert(typeof fiboEvenSum(10) === 'number');
+```
+
+Your function should return an even value.
+
+```js
+assert.equal(fiboEvenSum(10) % 2 === 0, true);
+```
+
+Your function should sum the even-valued Fibonacci numbers: `fiboEvenSum(8)` should return 10.
+
+```js
+assert.strictEqual(fiboEvenSum(8), 10);
+```
+
+`fiboEvenSum(10)` should return 10.
+
+```js
+assert.strictEqual(fiboEvenSum(10), 10);
+```
+
+`fiboEvenSum(34)` should return 44.
+
+```js
+assert.strictEqual(fiboEvenSum(34), 44);
+```
+
+`fiboEvenSum(60)` should return 44.
+
+```js
+assert.strictEqual(fiboEvenSum(60), 44);
+```
+
+`fiboEvenSum(1000)` should return 798.
+
+```js
+assert.strictEqual(fiboEvenSum(1000), 798);
+```
+
+`fiboEvenSum(100000)` should return 60696.
+
+```js
+assert.strictEqual(fiboEvenSum(100000), 60696);
+```
+
+`fiboEvenSum(4000000)` should return 4613732.
+
+```js
+assert.strictEqual(fiboEvenSum(4000000), 4613732);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function fiboEvenSum(n) {
+
+ return true;
+}
+```
+
+# --solutions--
+
+```js
+const fiboEvenSum = (number) => {
+ if (number <= 1) {
+ return 0;
+ } else {
+ let evenSum = 0,
+ prevFibNum = 1,
+ fibNum = 2; // According to problem description our Fibonacci series starts with 1, 2
+ for (let i = 2; fibNum <= number; i++) {
+ if (fibNum % 2 == 0) {
+ evenSum += fibNum;
+ }
+ [prevFibNum, fibNum] = [fibNum, prevFibNum + fibNum];
+ }
+ return evenSum;
+ }
+};
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-20-factorial-digit-sum.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-20-factorial-digit-sum.md
new file mode 100644
index 00000000000..a109ff5f9b2
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-20-factorial-digit-sum.md
@@ -0,0 +1,79 @@
+---
+id: 5900f3801000cf542c50fe93
+title: 'Problem 20: Factorial digit sum'
+challengeType: 1
+forumTopicId: 301839
+dashedName: problem-20-factorial-digit-sum
+---
+
+# --description--
+
+`n`! means `n` × (`n` − 1) × ... × 3 × 2 × 1
+
+For example, 10! = 10 × 9 × ... × 3 × 2 × 1 = 3628800,
+and the sum of the digits in the number 10! is 3 + 6 + 2 + 8 + 8 + 0 + 0 = 27.
+
+Find the sum of the digits `n`!
+
+# --hints--
+
+`sumFactorialDigits(10)` should return a number.
+
+```js
+assert(typeof sumFactorialDigits(10) === 'number');
+```
+
+`sumFactorialDigits(10)` should return 27.
+
+```js
+assert.strictEqual(sumFactorialDigits(10), 27);
+```
+
+`sumFactorialDigits(25)` should return 72.
+
+```js
+assert.strictEqual(sumFactorialDigits(25), 72);
+```
+
+`sumFactorialDigits(50)` should return 216.
+
+```js
+assert.strictEqual(sumFactorialDigits(50), 216);
+```
+
+`sumFactorialDigits(75)` should return 432.
+
+```js
+assert.strictEqual(sumFactorialDigits(75), 432);
+```
+
+`sumFactorialDigits(100)` should return 648.
+
+```js
+assert.strictEqual(sumFactorialDigits(100), 648);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumFactorialDigits(n) {
+
+ return n;
+}
+
+sumFactorialDigits(100);
+```
+
+# --solutions--
+
+```js
+let factorial = (n) => n <= 1 ? BigInt(n) : BigInt(n) * BigInt(factorial(--n));
+
+let sumDigits = n => n.toString().split('').map(x => parseInt(x)).reduce((a,b) => a + b);
+
+function sumFactorialDigits(n) {
+ return sumDigits(factorial(n));
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-21-amicable-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-21-amicable-numbers.md
new file mode 100644
index 00000000000..df19c7d7c20
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-21-amicable-numbers.md
@@ -0,0 +1,84 @@
+---
+id: 5900f3811000cf542c50fe94
+title: 'Problem 21: Amicable numbers'
+challengeType: 1
+forumTopicId: 301851
+dashedName: problem-21-amicable-numbers
+---
+
+# --description--
+
+Let d(`n`) be defined as the sum of proper divisors of `n` (numbers less than `n` which divide evenly into `n`).
+
+If d(`a`) = `b` and d(`b`) = `a`, where `a` ≠ `b`, then `a` and `b` are an amicable pair and each of `a` and `b` are called amicable numbers.
+
+For example, the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110; therefore d(220) = 284. The proper divisors of 284 are 1, 2, 4, 71 and 142; so d(284) = 220.
+
+Evaluate the sum of all the amicable numbers under `n`.
+
+# --hints--
+
+`sumAmicableNum(1000)` should return a number.
+
+```js
+assert(typeof sumAmicableNum(1000) === 'number');
+```
+
+`sumAmicableNum(1000)` should return 504.
+
+```js
+assert.strictEqual(sumAmicableNum(1000), 504);
+```
+
+`sumAmicableNum(2000)` should return 2898.
+
+```js
+assert.strictEqual(sumAmicableNum(2000), 2898);
+```
+
+`sumAmicableNum(5000)` should return 8442.
+
+```js
+assert.strictEqual(sumAmicableNum(5000), 8442);
+```
+
+`sumAmicableNum(10000)` should return 31626.
+
+```js
+assert.strictEqual(sumAmicableNum(10000), 31626);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumAmicableNum(n) {
+
+ return n;
+}
+
+sumAmicableNum(10000);
+```
+
+# --solutions--
+
+```js
+const sumAmicableNum = (n) => {
+ const fsum = (n) => {
+ let sum = 1;
+ for (let i = 2; i <= Math.floor(Math.sqrt(n)); i++)
+ if (Math.floor(n % i) === 0)
+ sum += i + Math.floor(n / i);
+ return sum;
+ };
+ let d = [];
+ let amicableSum = 0;
+ for (let i=2; i012 021 102 120 201 210
+
+What is the `n`th lexicographic permutation of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9?
+
+# --hints--
+
+`lexicographicPermutations(699999)` should return a number.
+
+```js
+assert(typeof lexicographicPermutations(699999) === 'number');
+```
+
+`lexicographicPermutations(699999)` should return 1938246570.
+
+```js
+assert(lexicographicPermutations(699999) == 1938246570);
+```
+
+`lexicographicPermutations(899999)` should return 2536987410.
+
+```js
+assert(lexicographicPermutations(899999) == 2536987410);
+```
+
+`lexicographicPermutations(900000)` should return 2537014689.
+
+```js
+assert(lexicographicPermutations(900000) == 2537014689);
+```
+
+`lexicographicPermutations(999999)` should return 2783915460.
+
+```js
+assert(lexicographicPermutations(999999) == 2783915460);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function lexicographicPermutations(n) {
+
+ return n;
+}
+
+lexicographicPermutations(999999);
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-25-1000-digit-fibonacci-number.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-25-1000-digit-fibonacci-number.md
new file mode 100644
index 00000000000..25d18d786ef
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-25-1000-digit-fibonacci-number.md
@@ -0,0 +1,85 @@
+---
+id: 5900f3851000cf542c50fe98
+title: 'Problem 25: 1000-digit Fibonacci number'
+challengeType: 1
+forumTopicId: 301897
+dashedName: problem-25-1000-digit-fibonacci-number
+---
+
+# --description--
+
+The Fibonacci sequence is defined by the recurrence relation:
+
+Fn = Fn−1 + Fn−2, where F1 = 1 and F2 = 1.
+
+Hence the first 12 terms will be:
+
+F1 = 1
F2 = 1
F3 = 2
F4 = 3
F5 = 5
F6 = 8
F7 = 13
F8 = 21
F9 = 34
F10 = 55
F11 = 89
F12 = 144
1/2 = 0.5
1/3 = 0.(3)
1/4 = 0.25
1/5 = 0.2
1/6 = 0.1(6)
1/7 = 0.(142857)
1/8 = 0.125
1/9 = 0.(1)
1/10 = 0.1
$n^2 + n + 41$
+
+It turns out that the formula will produce 40 primes for the consecutive integer values $0 \\le n \\le 39$. However, when $n = 40, 40^2 + 40 + 41 = 40(40 + 1) + 41$ is divisible by 41, and certainly when $n = 41, 41^2 + 41 + 41$ is clearly divisible by 41.
+
+The incredible formula $n^2 - 79n + 1601$ was discovered, which produces 80 primes for the consecutive values $0 \\le n \\le 79$. The product of the coefficients, −79 and 1601, is −126479.
+
+Considering quadratics of the form:
+
+
+ $n^2 + an + b$, where $|a| < range$ and $|b| \le range$
+ where $|n|$ is the modulus/absolute value of $n$
+ e.g. $|11| = 11$ and $|-4| = 4$
+
+
+Find the product of the coefficients, $a$ and $b$, for the quadratic expression that produces the maximum number of primes for consecutive values of $n$, starting with $n = 0$.
+
+# --hints--
+
+`quadraticPrimes(200)` should return a number.
+
+```js
+assert(typeof quadraticPrimes(200) === 'number');
+```
+
+`quadraticPrimes(200)` should return -4925.
+
+```js
+assert(quadraticPrimes(200) == -4925);
+```
+
+`quadraticPrimes(500)` should return -18901.
+
+```js
+assert(quadraticPrimes(500) == -18901);
+```
+
+`quadraticPrimes(800)` should return -43835.
+
+```js
+assert(quadraticPrimes(800) == -43835);
+```
+
+`quadraticPrimes(1000)` should return -59231.
+
+```js
+assert(quadraticPrimes(1000) == -59231);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function quadraticPrimes(range) {
+
+ return range;
+}
+
+quadraticPrimes(1000);
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-28-number-spiral-diagonals.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-28-number-spiral-diagonals.md
new file mode 100644
index 00000000000..eee50073f68
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-28-number-spiral-diagonals.md
@@ -0,0 +1,83 @@
+---
+id: 5900f3881000cf542c50fe9b
+title: 'Problem 28: Number spiral diagonals'
+challengeType: 1
+forumTopicId: 301930
+dashedName: problem-28-number-spiral-diagonals
+---
+
+# --description--
+
+Starting with the number 1 and moving to the right in a clockwise direction a 5 by 5 spiral is formed as follows:
+
++ where $|n|$ is the modulus/absolute value of $n$
+ e.g. $|11| = 11$ and $|-4| = 4$
+
+
+ 20
+ 19 6
+ 18
+
+
+
+It can be verified that the sum of the numbers on the diagonals is 101.
+
+What is the sum of the numbers on the diagonals in an `n` by `n` spiral formed in the same way?
+
+# --hints--
+
+`spiralDiagonals(101)` should return a number.
+
+```js
+assert(typeof spiralDiagonals(101) === 'number');
+```
+
+`spiralDiagonals(101)` should return 692101.
+
+```js
+assert(spiralDiagonals(101) == 692101);
+```
+
+`spiralDiagonals(303)` should return 18591725.
+
+```js
+assert(spiralDiagonals(303) == 18591725);
+```
+
+`spiralDiagonals(505)` should return 85986601.
+
+```js
+assert(spiralDiagonals(505) == 85986601);
+```
+
+`spiralDiagonals(1001)` should return 669171001.
+
+```js
+assert(spiralDiagonals(1001) == 669171001);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function spiralDiagonals(n) {
+
+ return n;
+}
+
+spiralDiagonals(1001);
+```
+
+# --solutions--
+
+```js
+const spiralDiagonals = (n) => {
+ const Sn2 = (n) => {
+ return n*(n+1)*(2*n+1)/6;
+ };
+ const Sn = (n) => {
+ return n*(n+1)/2;
+ };
+ let sum = (Sn2(n-1) + Sn(n-1) + n-1) + (Math.floor(n/2) + Sn2(n));
+ return sum;
+};
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-29-distinct-powers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-29-distinct-powers.md
new file mode 100644
index 00000000000..4b8f00162ee
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-29-distinct-powers.md
@@ -0,0 +1,86 @@
+---
+id: 5900f3891000cf542c50fe9c
+title: 'Problem 29: Distinct powers'
+challengeType: 1
+forumTopicId: 301941
+dashedName: problem-29-distinct-powers
+---
+
+# --description--
+
+Consider all integer combinations of $a^b$ for 2 ≤ a ≤ 5 and 2 ≤ b ≤ 5:
+
+21
22 23 24 25
+ 20
7
8 9
10+ 19 6
1
2 11+ 18
5
4 3
12+
17
16 15 14 13
+
+ 22=4, 23=8, 24=16, 25=32
+ 32=9, 33=27, 34=81, 35=243
+ 42=16, 43=64, 44=256, 45=1024
+ 52=25, 53=125, 54=625, 55=3125
+
+
+If they are then placed in numerical order, with any repeats removed, we get the following sequence of 15 distinct terms:
+
++ 32=9, 33=27, 34=81, 35=243
+ 42=16, 43=64, 44=256, 45=1024
+ 52=25, 53=125, 54=625, 55=3125
+
+ 4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125
+
+
+How many distinct terms are in the sequence generated by $a^b$ for 2 ≤ `a` ≤ `n` and 2 ≤ `b` ≤ `n`?
+
+# --hints--
+
+`distinctPowers(15)` should return a number.
+
+```js
+assert(typeof distinctPowers(15) === 'number');
+```
+
+`distinctPowers(15)` should return 177.
+
+```js
+assert.strictEqual(distinctPowers(15), 177);
+```
+
+`distinctPowers(20)` should return 324.
+
+```js
+assert.strictEqual(distinctPowers(20), 324);
+```
+
+`distinctPowers(25)` should return 519.
+
+```js
+assert.strictEqual(distinctPowers(25), 519);
+```
+
+`distinctPowers(30)` should return 755.
+
+```js
+assert.strictEqual(distinctPowers(30), 755);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function distinctPowers(n) {
+
+ return n;
+}
+
+distinctPowers(30);
+```
+
+# --solutions--
+
+```js
+const distinctPowers = (n) => {
+ let list = [];
+ for (let a=2; a<=n; a++) {
+ for (let b=2; b<=n; b++) {
+ let term = Math.pow(a, b);
+ if (list.indexOf(term)===-1) list.push(term);
+ }
+ }
+ return list.length;
+};
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-3-largest-prime-factor.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-3-largest-prime-factor.md
new file mode 100644
index 00000000000..2961ac6b9c0
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-3-largest-prime-factor.md
@@ -0,0 +1,95 @@
+---
+id: 5900f36f1000cf542c50fe82
+title: 'Problem 3: Largest prime factor'
+challengeType: 1
+forumTopicId: 301952
+dashedName: problem-3-largest-prime-factor
+---
+
+# --description--
+
+The prime factors of 13195 are 5, 7, 13 and 29.
+
+What is the largest prime factor of the given `number`?
+
+# --hints--
+
+`largestPrimeFactor(2)` should return a number.
+
+```js
+assert(typeof largestPrimeFactor(2) === 'number');
+```
+
+`largestPrimeFactor(2)` should return 2.
+
+```js
+assert.strictEqual(largestPrimeFactor(2), 2);
+```
+
+`largestPrimeFactor(3)` should return 3.
+
+```js
+assert.strictEqual(largestPrimeFactor(3), 3);
+```
+
+`largestPrimeFactor(5)` should return 5.
+
+```js
+assert.strictEqual(largestPrimeFactor(5), 5);
+```
+
+`largestPrimeFactor(7)` should return 7.
+
+```js
+assert.strictEqual(largestPrimeFactor(7), 7);
+```
+
+`largestPrimeFactor(8)` should return 2.
+
+```js
+assert.strictEqual(largestPrimeFactor(8), 2);
+```
+
+`largestPrimeFactor(13195)` should return 29.
+
+```js
+assert.strictEqual(largestPrimeFactor(13195), 29);
+```
+
+`largestPrimeFactor(600851475143)` should return 6857.
+
+```js
+assert.strictEqual(largestPrimeFactor(600851475143), 6857);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function largestPrimeFactor(number) {
+
+ return true;
+}
+
+largestPrimeFactor(13195);
+```
+
+# --solutions--
+
+```js
+const largestPrimeFactor = (number) => {
+ let largestFactor = number;
+
+ for (let i = 2; i <= Math.sqrt(largestFactor); i++) {
+ if (!(largestFactor % i)) {
+ let factor = largestFactor / i;
+ let candidate = largestPrimeFactor(factor);
+
+ return i > candidate ? i : candidate;
+ }
+ }
+
+ return largestFactor;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-30-digit-n-powers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-30-digit-n-powers.md
new file mode 100644
index 00000000000..1e7472bce84
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-30-digit-n-powers.md
@@ -0,0 +1,74 @@
+---
+id: 5900f38a1000cf542c50fe9d
+title: 'Problem 30: Digit n powers'
+challengeType: 1
+forumTopicId: 301953
+dashedName: problem-30-digit-n-powers
+---
+
+# --description--
+
+Surprisingly there are only three numbers that can be written as the sum of fourth powers of their digits:
+
+
+ 1634 = 14 + 64 + 34 + 44
+ 8208 = 84 + 24 + 04 + 84
+ 9474 = 94 + 44 + 74 + 44
+
+
+As 1 = 14 is not a sum it is not included.
+
+The sum of these numbers is 1634 + 8208 + 9474 = 19316.
+
+Find the sum of all the numbers that can be written as the sum of `n` powers of their digits.
+
+# --hints--
+
+`digitnPowers(2)` should return a number.
+
+```js
+assert(typeof digitnPowers(2) === 'number');
+```
+
+`digitnPowers(2)` should return 0.
+
+```js
+assert(digitnPowers(2) == 0);
+```
+
+`digitnPowers(3)` should return 1301.
+
+```js
+assert(digitnPowers(3) == 1301);
+```
+
+`digitnPowers(4)` should return 19316.
+
+```js
+assert(digitnPowers(4) == 19316);
+```
+
+`digitnPowers(5)` should return 443839.
+
+```js
+assert(digitnPowers(5) == 443839);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function digitnPowers(n) {
+
+ return n;
+}
+
+digitnPowers(5);
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-31-coin-sums.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-31-coin-sums.md
new file mode 100644
index 00000000000..ae4372cd69f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-31-coin-sums.md
@@ -0,0 +1,77 @@
+---
+id: 5900f38b1000cf542c50fe9e
+title: 'Problem 31: Coin sums'
+challengeType: 1
+forumTopicId: 301965
+dashedName: problem-31-coin-sums
+---
+
+# --description--
+
+In England the currency is made up of pound, £, and pence, p, and there are eight coins in general circulation:
+
++ 8208 = 84 + 24 + 04 + 84
+ 9474 = 94 + 44 + 74 + 44
+
1p, 2p, 5p, 10p, 20p, 50p, £1 (100p) and £2 (200p).
+
+It is possible to make £2 in the following way:
+
+1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p
+
+How many different ways can `n` pence be made using any number of coins?
+
+# --hints--
+
+`coinSums(50)` should return a number.
+
+```js
+assert(typeof coinSums(50) === 'number');
+```
+
+`coinSums(50)` should return 451.
+
+```js
+assert(coinSums(50) == 451);
+```
+
+`coinSums(100)` should return 4563.
+
+```js
+assert(coinSums(100) == 4563);
+```
+
+`coinSums(150)` should return 21873.
+
+```js
+assert(coinSums(150) == 21873);
+```
+
+`coinSums(200)` should return 73682.
+
+```js
+assert(coinSums(200) == 73682);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function coinSums(n) {
+
+ return n;
+}
+
+coinSums(200);
+```
+
+# --solutions--
+
+```js
+const coinSums = (n) => {
+ const getWays = (n, m=8, c=[1, 2, 5, 10, 20, 50, 100, 200]) => {
+ if (n === 0) return 1;
+ if (m === 0 || n < 0) return 0;
+ return getWays(n - c[m - 1], m, c) + getWays(n, m - 1, c);
+ };
+ return getWays(n);
+};
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-32-pandigital-products.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-32-pandigital-products.md
new file mode 100644
index 00000000000..5fe7d0495c5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-32-pandigital-products.md
@@ -0,0 +1,118 @@
+---
+id: 5900f38c1000cf542c50fe9f
+title: 'Problem 32: Pandigital products'
+challengeType: 1
+forumTopicId: 301976
+dashedName: problem-32-pandigital-products
+---
+
+# --description--
+
+We shall say that an `n`-digit number is pandigital if it makes use of all the digits 1 to `n` exactly once; for example, the 5-digit number, 15234, is 1 through 5 pandigital.
+
+The product 7254 is unusual, as the identity, 39 × 186 = 7254, containing multiplicand, multiplier, and product is 1 through 9 pandigital.
+
+Find the sum of all products whose multiplicand/multiplier/product identity can be written as a 1 through `n` pandigital.
+
+**Hint:** Some products can be obtained in more than one way so be sure to only include it once in your sum.
+
+# --hints--
+
+`pandigitalProducts(4)` should return a number.
+
+```js
+assert(typeof pandigitalProducts(4) === 'number');
+```
+
+`pandigitalProducts(4)` should return `12`.
+
+```js
+assert.strictEqual(pandigitalProducts(4), 12);
+```
+
+`pandigitalProducts(6)` should return `162`.
+
+```js
+assert.strictEqual(pandigitalProducts(6), 162);
+```
+
+`pandigitalProducts(7)` should return `0`.
+
+```js
+assert.strictEqual(pandigitalProducts(7), 0);
+```
+
+`pandigitalProducts(8)` should return `13458`.
+
+```js
+assert.strictEqual(pandigitalProducts(8), 13458);
+```
+
+`pandigitalProducts(9)` should return `45228`.
+
+```js
+assert.strictEqual(pandigitalProducts(9), 45228);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pandigitalProducts(n) {
+
+ return true;
+}
+
+pandigitalProducts(4);
+```
+
+# --solutions--
+
+```js
+function pandigitalProducts(n) {
+ function is1toNPandigital(n, digitStr) {
+ // check if length is n
+ if (digitStr.length !== n) {
+ return false;
+ }
+ // check if pandigital
+ for (let i = digitStr.length; i > 0; i--) {
+ if (digitStr.indexOf(i.toString()) === -1) {
+ return false;
+ }
+ }
+ return true;
+ }
+ function concatenateNums(...numbers) {
+ let digitStr = '';
+ for (let i = 0; i < numbers.length; i++) {
+ digitStr += numbers[i].toString();
+ }
+ return digitStr;
+ }
+
+ const pandigitalNums = [];
+ const limit = 10 ** Math.floor(n / 2) - 1;
+ let sum = 0;
+ for (let mult1 = 2; mult1 < limit; mult1++) {
+ for (let mult2 = 2; mult2 < limit; mult2++) {
+ const product = mult1 * mult2;
+ const concatenated = concatenateNums(mult1, mult2, product);
+ if (concatenated.length > n) {
+ break;
+ } else if (concatenated.length < n) {
+ continue;
+ }
+ if (
+ is1toNPandigital(n, concatenated) &&
+ !pandigitalNums.includes(product)
+ ) {
+ pandigitalNums.push(product);
+ sum += product;
+ }
+ }
+ }
+ return sum;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-33-digit-cancelling-fractions.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-33-digit-cancelling-fractions.md
new file mode 100644
index 00000000000..5419f2f8270
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-33-digit-cancelling-fractions.md
@@ -0,0 +1,102 @@
+---
+id: 5900f38d1000cf542c50fea0
+title: 'Problem 33: Digit cancelling fractions'
+challengeType: 1
+forumTopicId: 301987
+dashedName: problem-33-digit-cancelling-fractions
+---
+
+# --description--
+
+The fraction 49/98 is a curious fraction, as an inexperienced mathematician in attempting to simplify it may incorrectly believe that 49/98 = 4/8, which is correct, is obtained by cancelling the 9s.
+
+We shall consider fractions like, 30/50 = 3/5, to be trivial examples.
+
+There are exactly four non-trivial examples of this type of fraction, less than one in value, and containing two digits in the numerator and denominator.
+
+If the product of these four fractions is given in its lowest common terms, find the value of the denominator.
+
+# --hints--
+
+`digitCancellingFractions()` should return a number.
+
+```js
+assert(typeof digitCancellingFractions() === 'number');
+```
+
+`digitCancellingFractions()` should return 100.
+
+```js
+assert.strictEqual(digitCancellingFractions(), 100);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function digitCancellingFractions() {
+
+ return true;
+}
+
+digitCancellingFractions();
+```
+
+# --solutions--
+
+```js
+function digitCancellingFractions() {
+ function isCurious(numerator, denominator) {
+ const fraction = numerator / denominator;
+ const numString = numerator.toString();
+ const denString = denominator.toString();
+
+ if (numString[1] === '0' && denString[1] === '0') {
+ // trivial
+ return false;
+ }
+ for (let i = 0; i < 2; i++) {
+ for (let j = 0; j < 2; j++) {
+ if (numString[i] === denString[j]) {
+ const newNum = parseInt(numString[1 - i], 10);
+ const newDen = parseInt(denString[1 - j], 10);
+ if (newNum / newDen === fraction) {
+ return true;
+ }
+ }
+ }
+ }
+ return false;
+ }
+ function findLargestDivisor(a, b) {
+ let gcd = a > b ? b : a;
+ while (gcd > 1) {
+ if (a % gcd === 0 && b % gcd === 0) {
+ return gcd;
+ }
+ gcd--;
+ }
+ return gcd;
+ }
+
+ function simplifyFraction(numerator, denominator) {
+ const divisor = findLargestDivisor(numerator, denominator);
+ return [numerator / divisor, denominator / divisor];
+ }
+
+ let multipleNumerator = 1;
+ let multipleDenominator = 1;
+
+ for (let denominator = 11; denominator < 100; denominator++) {
+ for (let numerator = 10; numerator < denominator; numerator++) {
+ if (isCurious(numerator, denominator)) {
+ multipleNumerator *= numerator;
+ multipleDenominator *= denominator;
+ }
+ }
+ }
+
+ return simplifyFraction(multipleNumerator, multipleDenominator)[1];
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-34-digit-factorials.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-34-digit-factorials.md
new file mode 100644
index 00000000000..2eb87f93ba1
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-34-digit-factorials.md
@@ -0,0 +1,50 @@
+---
+id: 5900f38e1000cf542c50fea1
+title: 'Problem 34: Digit factorials'
+challengeType: 1
+forumTopicId: 301998
+dashedName: problem-34-digit-factorials
+---
+
+# --description--
+
+145 is a curious number, as 1! + 4! + 5! = 1 + 24 + 120 = 145.
+
+Find the numbers and the sum of the numbers which are equal to the sum of the factorial of their digits.
+
+**Note:** as 1! = 1 and 2! = 2 are not sums they are not included.
+
+# --hints--
+
+`digitFactorial()` should return an object.
+
+```js
+assert.typeOf(digitFactorial(), 'object');
+```
+
+`digitFactorial()` should return { sum: 40730, numbers: [145, 40585] }.
+
+```js
+assert.deepEqual(digitFactorial(), { sum: 40730, numbers: [145, 40585] });
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function digitFactorial() {
+
+ var sum = 0;
+ var numbers = [];
+ return { sum, numbers };
+}
+
+digitFactorial();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-35-circular-primes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-35-circular-primes.md
new file mode 100644
index 00000000000..aaae9562bb0
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-35-circular-primes.md
@@ -0,0 +1,132 @@
+---
+id: 5900f38f1000cf542c50fea2
+title: 'Problem 35: Circular primes'
+challengeType: 1
+forumTopicId: 302009
+dashedName: problem-35-circular-primes
+---
+
+# --description--
+
+The number, 197, is called a circular prime because all rotations of the digits: 197, 971, and 719, are themselves prime.
+
+There are thirteen such primes below 100: 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, and 97.
+
+How many circular primes are there below `n`, whereas 100 ≤ `n` ≤ 1000000?
+
+**Note:**
+
+Circular primes individual rotation can exceed `n`.
+
+# --hints--
+
+`circularPrimes(100)` should return a number.
+
+```js
+assert(typeof circularPrimes(100) === 'number');
+```
+
+`circularPrimes(100)` should return 13.
+
+```js
+assert(circularPrimes(100) == 13);
+```
+
+`circularPrimes(100000)` should return 43.
+
+```js
+assert(circularPrimes(100000) == 43);
+```
+
+`circularPrimes(250000)` should return 45.
+
+```js
+assert(circularPrimes(250000) == 45);
+```
+
+`circularPrimes(500000)` should return 49.
+
+```js
+assert(circularPrimes(500000) == 49);
+```
+
+`circularPrimes(750000)` should return 49.
+
+```js
+assert(circularPrimes(750000) == 49);
+```
+
+`circularPrimes(1000000)` should return 55.
+
+```js
+assert(circularPrimes(1000000) == 55);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function circularPrimes(n) {
+
+ return n;
+}
+
+circularPrimes(1000000);
+```
+
+# --solutions--
+
+```js
+function rotate(n) {
+ if (n.length == 1) return n;
+ return n.slice(1) + n[0];
+}
+
+function circularPrimes(n) {
+ // Nearest n < 10^k
+ const bound = 10 ** Math.ceil(Math.log10(n));
+ const primes = [0, 0, 2];
+ let count = 0;
+
+ // Making primes array
+ for (let i = 4; i <= bound; i += 2) {
+ primes.push(i - 1);
+ primes.push(0);
+ }
+
+ // Getting upperbound
+ const upperBound = Math.ceil(Math.sqrt(bound));
+
+ // Setting other non-prime numbers to 0
+ for (let i = 3; i < upperBound; i += 2) {
+ if (primes[i]) {
+ for (let j = i * i; j < bound; j += i) {
+ primes[j] = 0;
+ }
+ }
+ }
+
+ // Iterating through the array
+ for (let i = 2; i < n; i++) {
+ if (primes[i]) {
+ let curr = String(primes[i]);
+ let tmp = 1; // tmp variable to hold the no of rotations
+ for (let x = rotate(curr); x != curr; x = rotate(x)) {
+ if (x > n && primes[x]) {
+ continue;
+ }
+ else if (!primes[x]) {
+ // If the rotated value is 0 then it isn't a circular prime, break the loop
+ tmp = 0;
+ break;
+ }
+ tmp++;
+ primes[x] = 0;
+ }
+ count += tmp;
+ }
+ }
+ return count;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-36-double-base-palindromes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-36-double-base-palindromes.md
new file mode 100644
index 00000000000..9793d760c20
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-36-double-base-palindromes.md
@@ -0,0 +1,66 @@
+---
+id: 5900f3901000cf542c50fea3
+title: 'Problem 36: Double-base palindromes'
+challengeType: 1
+forumTopicId: 302020
+dashedName: problem-36-double-base-palindromes
+---
+
+# --description--
+
+The decimal number, 585 = 10010010012 (binary), is palindromic in both bases.
+
+Find the sum of all numbers, less than `n`, whereas 1000 ≤ `n` ≤ 1000000, which are palindromic in base 10 and base 2.
+
+(Please note that the palindromic number, in either base, may not include leading zeros.)
+
+# --hints--
+
+`doubleBasePalindromes(1000)` should return a number.
+
+```js
+assert(typeof doubleBasePalindromes(1000) === 'number');
+```
+
+`doubleBasePalindromes(1000)` should return 1772.
+
+```js
+assert(doubleBasePalindromes(1000) == 1772);
+```
+
+`doubleBasePalindromes(50000)` should return 105795.
+
+```js
+assert(doubleBasePalindromes(50000) == 105795);
+```
+
+`doubleBasePalindromes(500000)` should return 286602.
+
+```js
+assert(doubleBasePalindromes(500000) == 286602);
+```
+
+`doubleBasePalindromes(1000000)` should return 872187.
+
+```js
+assert(doubleBasePalindromes(1000000) == 872187);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function doubleBasePalindromes(n) {
+
+ return n;
+}
+
+doubleBasePalindromes(1000000);
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-37-truncatable-primes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-37-truncatable-primes.md
new file mode 100644
index 00000000000..5d4c80d5252
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-37-truncatable-primes.md
@@ -0,0 +1,66 @@
+---
+id: 5900f3911000cf542c50fea4
+title: 'Problem 37: Truncatable primes'
+challengeType: 1
+forumTopicId: 302031
+dashedName: problem-37-truncatable-primes
+---
+
+# --description--
+
+The number 3797 has an interesting property. Being prime itself, it is possible to continuously remove digits from left to right, and remain prime at each stage: 3797, 797, 97, and 7. Similarly we can work from right to left: 3797, 379, 37, and 3.
+
+Find the sum of the only `n` (8 ≤ `n` ≤ 11) primes that are both truncatable from left to right and right to left.
+
+NOTE: 2, 3, 5, and 7 are not considered to be truncatable primes.
+
+# --hints--
+
+`truncatablePrimes(8)` should return a number.
+
+```js
+assert(typeof truncatablePrimes(8) === 'number');
+```
+
+`truncatablePrimes(8)` should return 1986.
+
+```js
+assert(truncatablePrimes(8) == 1986);
+```
+
+`truncatablePrimes(9)` should return 5123.
+
+```js
+assert(truncatablePrimes(9) == 5123);
+```
+
+`truncatablePrimes(10)` should return 8920.
+
+```js
+assert(truncatablePrimes(10) == 8920);
+```
+
+`truncatablePrimes(11)` should return 748317.
+
+```js
+assert(truncatablePrimes(11) == 748317);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function truncatablePrimes(n) {
+
+ return n;
+}
+
+truncatablePrimes(11);
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-38-pandigital-multiples.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-38-pandigital-multiples.md
new file mode 100644
index 00000000000..a1190e84f39
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-38-pandigital-multiples.md
@@ -0,0 +1,98 @@
+---
+id: 5900f3931000cf542c50fea5
+title: 'Problem 38: Pandigital multiples'
+challengeType: 1
+forumTopicId: 302042
+dashedName: problem-38-pandigital-multiples
+---
+
+# --description--
+
+Take the number 192 and multiply it by each of 1, 2, and 3:
+
+$$\begin{align} 192 × 1 = 192\\\\
+ 192 × 2 = 384\\\\ 192 × 3 = 576\\\\
+\end{align}$$
+
+By concatenating each product we get the 1 to 9 pandigital, 192384576. We will call 192384576 the concatenated product of 192 and (1, 2, 3).
+
+The same can be achieved by starting with 9 and multiplying by 1, 2, 3, 4, and 5, giving the pandigital, 918273645, which is the concatenated product of 9 and (1, 2, 3, 4, 5).
+
+What is the largest 1 to `k` pandigital `k`-digit number that can be formed as the concatenated product of an integer with (1, 2, ..., `n`) where `n` > 1?
+
+# --hints--
+
+`pandigitalMultiples(8)` should return a number.
+
+```js
+assert(typeof pandigitalMultiples(8) === 'number');
+```
+
+`pandigitalMultiples(8)` should return `78156234`.
+
+```js
+assert.strictEqual(pandigitalMultiples(8), 78156234);
+```
+
+`pandigitalMultiples(9)` should return `932718654`.
+
+```js
+assert.strictEqual(pandigitalMultiples(9), 932718654);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pandigitalMultiples(k) {
+
+ return true;
+}
+
+pandigitalMultiples(8);
+```
+
+# --solutions--
+
+```js
+function pandigitalMultiples(k) {
+ function getKDigitConcatenatedProduct(num, k) {
+ // returns false if concatenated product is not k digits
+ let concatenatedProduct = num.toString();
+ for (let i = 2; concatenatedProduct.length < k; i++) {
+ concatenatedProduct += num * i;
+ }
+ return concatenatedProduct.length === k ? concatenatedProduct : false;
+ }
+
+ function is1toKPandigital(num, k) {
+ const numStr = num.toString();
+
+ // check if length is not k
+ if (numStr.length !== k) {
+ return false;
+ }
+
+ // check if pandigital
+ for (let i = k; i > 0; i--) {
+ if (numStr.indexOf(i.toString()) === -1) {
+ return false;
+ }
+ }
+ return true;
+ }
+
+ let largestNum = 0;
+ for (let i = 10 ** Math.floor(k / 2) + 1; i >= 1; i--) {
+ const concatenatedProduct = getKDigitConcatenatedProduct(i, k);
+ if (is1toKPandigital(concatenatedProduct, k)) {
+ const number = parseInt(concatenatedProduct, 10);
+ if (number > largestNum) {
+ largestNum = number;
+ }
+ }
+ }
+ return largestNum;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-39-integer-right-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-39-integer-right-triangles.md
new file mode 100644
index 00000000000..f1957262624
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-39-integer-right-triangles.md
@@ -0,0 +1,91 @@
+---
+id: 5900f3931000cf542c50fea6
+title: 'Problem 39: Integer right triangles'
+challengeType: 1
+forumTopicId: 302054
+dashedName: problem-39-integer-right-triangles
+---
+
+# --description--
+
+If `p` is the perimeter of a right angle triangle with integral length sides, {a,b,c}, there are exactly three solutions for p = 120.
+
+{20,48,52}, {24,45,51}, {30,40,50}
+
+For which value of `p` ≤ `n`, is the number of solutions maximized?
+
+# --hints--
+
+`intRightTriangles(500)` should return a number.
+
+```js
+assert(typeof intRightTriangles(500) === 'number');
+```
+
+`intRightTriangles(500)` should return 420.
+
+```js
+assert(intRightTriangles(500) == 420);
+```
+
+`intRightTriangles(800)` should return 720.
+
+```js
+assert(intRightTriangles(800) == 720);
+```
+
+`intRightTriangles(900)` should return 840.
+
+```js
+assert(intRightTriangles(900) == 840);
+```
+
+`intRightTriangles(1000)` should return 840.
+
+```js
+assert(intRightTriangles(1000) == 840);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function intRightTriangles(n) {
+
+ return n;
+}
+
+intRightTriangles(500);
+```
+
+# --solutions--
+
+```js
+// Original idea for this solution came from
+// https://www.xarg.org/puzzle/project-euler/problem-39/
+
+function intRightTriangles(n) {
+ // store the number of triangles with a given perimeter
+ let triangles = {};
+ // a is the shortest side
+ for (let a = 3; a < n / 3; a++)
+ // o is the opposite side and is at least as long as a
+ for (let o = a; o < n / 2; o++) {
+ let h = Math.sqrt(a * a + o * o); // hypotenuse
+ let p = a + o + h; // perimeter
+ if ((h % 1) === 0 && p <= n) {
+ triangles[p] = (triangles[p] || 0) + 1;
+ }
+ }
+
+ let max = 0, maxp = null;
+ for (let p in triangles) {
+ if (max < triangles[p]) {
+ max = triangles[p];
+ maxp = parseInt(p);
+ }
+ }
+ return maxp;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-4-largest-palindrome-product.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-4-largest-palindrome-product.md
new file mode 100644
index 00000000000..9e436255531
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-4-largest-palindrome-product.md
@@ -0,0 +1,64 @@
+---
+id: 5900f3701000cf542c50fe83
+title: 'Problem 4: Largest palindrome product'
+challengeType: 1
+forumTopicId: 302065
+dashedName: problem-4-largest-palindrome-product
+---
+
+# --description--
+
+A palindromic number reads the same both ways. The largest palindrome made from the product of two 2-digit numbers is 9009 = 91 × 99.
+
+Find the largest palindrome made from the product of two `n`-digit numbers.
+
+# --hints--
+
+`largestPalindromeProduct(2)` should return a number.
+
+```js
+assert(typeof largestPalindromeProduct(2) === 'number');
+```
+
+`largestPalindromeProduct(2)` should return 9009.
+
+```js
+assert.strictEqual(largestPalindromeProduct(2), 9009);
+```
+
+`largestPalindromeProduct(3)` should return 906609.
+
+```js
+assert.strictEqual(largestPalindromeProduct(3), 906609);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function largestPalindromeProduct(n) {
+
+ return true;
+}
+
+largestPalindromeProduct(3);
+```
+
+# --solutions--
+
+```js
+const largestPalindromeProduct = (digit)=>{
+ let start = 1;
+ let end = Number(`1e${digit}`) - 1;
+ let palindrome = [];
+ for(let i=start;i<=end;i++){
+ for(let j=start;j<=end;j++){
+ let product = i*j;
+ let palindromeRegex = /\b(\d)(\d?)(\d?).?\3\2\1\b/gi;
+ palindromeRegex.test(product) && palindrome.push(product);
+ }
+ }
+ return Math.max(...palindrome);
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-40-champernownes-constant.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-40-champernownes-constant.md
new file mode 100644
index 00000000000..c4386bd2d91
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-40-champernownes-constant.md
@@ -0,0 +1,77 @@
+---
+id: 5900f3941000cf542c50fea7
+title: 'Problem 40: Champernowne''s constant'
+challengeType: 1
+forumTopicId: 302066
+dashedName: problem-40-champernownes-constant
+---
+
+# --description--
+
+An irrational decimal fraction is created by concatenating the positive integers:
+
+0.12345678910**1**112131415161718192021...
+
+It can be seen that the 12th digit of the fractional part is 1.
+
+If *dn* represents the *n*th digit of the fractional part, find the value of the following expression.
+
+d1 × d10 × d100 × d1000 × d10000 × d100000 × d1000000
+
+# --hints--
+
+`champernownesConstant(100)` should return a number.
+
+```js
+assert(typeof champernownesConstant(100) === 'number');
+```
+
+`champernownesConstant(100)` should return 5.
+
+```js
+assert.strictEqual(champernownesConstant(100), 5);
+```
+
+`champernownesConstant(1000)` should return 15.
+
+```js
+assert.strictEqual(champernownesConstant(1000), 15);
+```
+
+`champernownesConstant(1000000)` should return 210.
+
+```js
+assert.strictEqual(champernownesConstant(1000000), 210);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function champernownesConstant(n) {
+
+ return true;
+}
+
+champernownesConstant(100);
+```
+
+# --solutions--
+
+```js
+function champernownesConstant(n) {
+ let fractionalPart = '';
+ for (let i = 0; fractionalPart.length <= n; i++) {
+ fractionalPart += i.toString();
+ }
+
+ let product = 1;
+ for (let i = 0; i < n.toString().length; i++) {
+ const index = 10 ** i;
+ product *= parseInt(fractionalPart[index], 10);
+ }
+
+ return product;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-41-pandigital-prime.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-41-pandigital-prime.md
new file mode 100644
index 00000000000..a774fa31167
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-41-pandigital-prime.md
@@ -0,0 +1,117 @@
+---
+id: 5900f3951000cf542c50fea8
+title: 'Problem 41: Pandigital prime'
+challengeType: 1
+forumTopicId: 302078
+dashedName: problem-41-pandigital-prime
+---
+
+# --description--
+
+We shall say that an `n`-digit number is pandigital if it makes use of all the digits 1 to `n` exactly once. For example, 2143 is a 4-digit pandigital and is also prime.
+
+What is the largest `n`-length digit pandigital prime that exists?
+
+# --hints--
+
+`pandigitalPrime(4)` should return a number.
+
+```js
+assert(typeof pandigitalPrime(4) === 'number');
+```
+
+`pandigitalPrime(4)` should return 4231.
+
+```js
+assert(pandigitalPrime(4) == 4231);
+```
+
+`pandigitalPrime(7)` should return 7652413.
+
+```js
+assert(pandigitalPrime(7) == 7652413);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pandigitalPrime(n) {
+
+ return n;
+}
+
+pandigitalPrime(7);
+```
+
+# --solutions--
+
+```js
+function pandigitalPrime(n) {
+ function isPrime(num) {
+ for (let i = 2, s = Math.sqrt(num); i <= s; i++) {
+ if (num % i === 0) {
+ return false;
+ }
+ }
+ return num !== 1;
+ }
+
+ function getPermutations(n) {
+ if (n === 1) {
+ permutations.push(digitsArr.join(''));
+ } else {
+ for (let i = 0; i < n - 1; i++) {
+ getPermutations(n - 1);
+ // swap(n % 2 === 0 ? i : 0, n - 1);
+ if (n % 2 === 0) {
+ swap(i, n - 1);
+ } else {
+ swap(0, n - 1);
+ }
+ }
+ getPermutations(n - 1);
+ }
+ }
+ function swap(x, y) {
+ let temp = digitsArr[x];
+ digitsArr[x] = digitsArr[y];
+ digitsArr[y] = temp;
+ }
+ let max = 0;
+ let permutations = [];
+ let digitsArr;
+ let pandigitalNum = '';
+
+ for (let max = n; max > 0; max--) {
+ pandigitalNum += max;
+ }
+
+ for (let i = 0; i < pandigitalNum.length; i++) {
+ if (max > 0) {
+ break;
+ } else {
+ permutations = [];
+ const currMax = pandigitalNum.slice(i);
+ digitsArr = currMax.split('');
+ getPermutations(digitsArr.length);
+
+ // sort permutations in descending order
+ permutations.sort(function(a, b) {
+ return b - a;
+ });
+
+ for (let perm of permutations) {
+ const thisPerm = parseInt(perm);
+ if (isPrime(thisPerm)) {
+ max = thisPerm;
+ break;
+ }
+ }
+ }
+ }
+
+ return max;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-42-coded-triangle-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-42-coded-triangle-numbers.md
new file mode 100644
index 00000000000..abda6f2d137
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-42-coded-triangle-numbers.md
@@ -0,0 +1,71 @@
+---
+id: 5900f3961000cf542c50fea9
+title: 'Problem 42: Coded triangle numbers'
+challengeType: 1
+forumTopicId: 302089
+dashedName: problem-42-coded-triangle-numbers
+---
+
+# --description--
+
+The `n`th term of the sequence of triangle numbers is given by, `tn` = ½`n`(`n`+1); so the first ten triangle numbers are:
+
+1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...
+
+By converting each letter in a word to a number corresponding to its alphabetical position and adding these values we form a word value. For example, the word value for SKY is 19 + 11 + 25 = 55 = `t`10. If the word value is a triangle number then we shall call the word a triangle word.
+
+Using words array of `n`-length, how many are triangle words?
+
+# --hints--
+
+`codedTriangleNumbers(1400)` should return a number.
+
+```js
+assert(typeof codedTriangleNumbers(1400) === 'number');
+```
+
+`codedTriangleNumbers(1400)` should return 129.
+
+```js
+assert(codedTriangleNumbers(1400) == 129);
+```
+
+`codedTriangleNumbers(1500)` should return 137.
+
+```js
+assert(codedTriangleNumbers(1500) == 137);
+```
+
+`codedTriangleNumbers(1600)` should return 141.
+
+```js
+assert(codedTriangleNumbers(1600) == 141);
+```
+
+`codedTriangleNumbers(1786)` should return 162.
+
+```js
+assert(codedTriangleNumbers(1786) == 162);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function codedTriangleNumbers(n) {
+
+ return 1;
+}
+// Only change code above this line
+
+const words = ['A','ABILITY','ABLE','ABOUT','ABOVE','ABSENCE','ABSOLUTELY','ACADEMIC','ACCEPT','ACCESS','ACCIDENT','ACCOMPANY','ACCORDING','ACCOUNT','ACHIEVE','ACHIEVEMENT','ACID','ACQUIRE','ACROSS','ACT','ACTION','ACTIVE','ACTIVITY','ACTUAL','ACTUALLY','ADD','ADDITION','ADDITIONAL','ADDRESS','ADMINISTRATION','ADMIT','ADOPT','ADULT','ADVANCE','ADVANTAGE','ADVICE','ADVISE','AFFAIR','AFFECT','AFFORD','AFRAID','AFTER','AFTERNOON','AFTERWARDS','AGAIN','AGAINST','AGE','AGENCY','AGENT','AGO','AGREE','AGREEMENT','AHEAD','AID','AIM','AIR','AIRCRAFT','ALL','ALLOW','ALMOST','ALONE','ALONG','ALREADY','ALRIGHT','ALSO','ALTERNATIVE','ALTHOUGH','ALWAYS','AMONG','AMONGST','AMOUNT','AN','ANALYSIS','ANCIENT','AND','ANIMAL','ANNOUNCE','ANNUAL','ANOTHER','ANSWER','ANY','ANYBODY','ANYONE','ANYTHING','ANYWAY','APART','APPARENT','APPARENTLY','APPEAL','APPEAR','APPEARANCE','APPLICATION','APPLY','APPOINT','APPOINTMENT','APPROACH','APPROPRIATE','APPROVE','AREA','ARGUE','ARGUMENT','ARISE','ARM','ARMY','AROUND','ARRANGE','ARRANGEMENT','ARRIVE','ART','ARTICLE','ARTIST','AS','ASK','ASPECT','ASSEMBLY','ASSESS','ASSESSMENT','ASSET','ASSOCIATE','ASSOCIATION','ASSUME','ASSUMPTION','AT','ATMOSPHERE','ATTACH','ATTACK','ATTEMPT','ATTEND','ATTENTION','ATTITUDE','ATTRACT','ATTRACTIVE','AUDIENCE','AUTHOR','AUTHORITY','AVAILABLE','AVERAGE','AVOID','AWARD','AWARE','AWAY','AYE','BABY','BACK','BACKGROUND','BAD','BAG','BALANCE','BALL','BAND','BANK','BAR','BASE','BASIC','BASIS','BATTLE','BE','BEAR','BEAT','BEAUTIFUL','BECAUSE','BECOME','BED','BEDROOM','BEFORE','BEGIN','BEGINNING','BEHAVIOUR','BEHIND','BELIEF','BELIEVE','BELONG','BELOW','BENEATH','BENEFIT','BESIDE','BEST','BETTER','BETWEEN','BEYOND','BIG','BILL','BIND','BIRD','BIRTH','BIT','BLACK','BLOCK','BLOOD','BLOODY','BLOW','BLUE','BOARD','BOAT','BODY','BONE','BOOK','BORDER','BOTH','BOTTLE','BOTTOM','BOX','BOY','BRAIN','BRANCH','BREAK','BREATH','BRIDGE','BRIEF','BRIGHT','BRING','BROAD','BROTHER','BUDGET','BUILD','BUILDING','BURN','BUS','BUSINESS','BUSY','BUT','BUY','BY','CABINET','CALL','CAMPAIGN','CAN','CANDIDATE','CAPABLE','CAPACITY','CAPITAL','CAR','CARD','CARE','CAREER','CAREFUL','CAREFULLY','CARRY','CASE','CASH','CAT','CATCH','CATEGORY','CAUSE','CELL','CENTRAL','CENTRE','CENTURY','CERTAIN','CERTAINLY','CHAIN','CHAIR','CHAIRMAN','CHALLENGE','CHANCE','CHANGE','CHANNEL','CHAPTER','CHARACTER','CHARACTERISTIC','CHARGE','CHEAP','CHECK','CHEMICAL','CHIEF','CHILD','CHOICE','CHOOSE','CHURCH','CIRCLE','CIRCUMSTANCE','CITIZEN','CITY','CIVIL','CLAIM','CLASS','CLEAN','CLEAR','CLEARLY','CLIENT','CLIMB','CLOSE','CLOSELY','CLOTHES','CLUB','COAL','CODE','COFFEE','COLD','COLLEAGUE','COLLECT','COLLECTION','COLLEGE','COLOUR','COMBINATION','COMBINE','COME','COMMENT','COMMERCIAL','COMMISSION','COMMIT','COMMITMENT','COMMITTEE','COMMON','COMMUNICATION','COMMUNITY','COMPANY','COMPARE','COMPARISON','COMPETITION','COMPLETE','COMPLETELY','COMPLEX','COMPONENT','COMPUTER','CONCENTRATE','CONCENTRATION','CONCEPT','CONCERN','CONCERNED','CONCLUDE','CONCLUSION','CONDITION','CONDUCT','CONFERENCE','CONFIDENCE','CONFIRM','CONFLICT','CONGRESS','CONNECT','CONNECTION','CONSEQUENCE','CONSERVATIVE','CONSIDER','CONSIDERABLE','CONSIDERATION','CONSIST','CONSTANT','CONSTRUCTION','CONSUMER','CONTACT','CONTAIN','CONTENT','CONTEXT','CONTINUE','CONTRACT','CONTRAST','CONTRIBUTE','CONTRIBUTION','CONTROL','CONVENTION','CONVERSATION','COPY','CORNER','CORPORATE','CORRECT','COS','COST','COULD','COUNCIL','COUNT','COUNTRY','COUNTY','COUPLE','COURSE','COURT','COVER','CREATE','CREATION','CREDIT','CRIME','CRIMINAL','CRISIS','CRITERION','CRITICAL','CRITICISM','CROSS','CROWD','CRY','CULTURAL','CULTURE','CUP','CURRENT','CURRENTLY','CURRICULUM','CUSTOMER','CUT','DAMAGE','DANGER','DANGEROUS','DARK','DATA','DATE','DAUGHTER','DAY','DEAD','DEAL','DEATH','DEBATE','DEBT','DECADE','DECIDE','DECISION','DECLARE','DEEP','DEFENCE','DEFENDANT','DEFINE','DEFINITION','DEGREE','DELIVER','DEMAND','DEMOCRATIC','DEMONSTRATE','DENY','DEPARTMENT','DEPEND','DEPUTY','DERIVE','DESCRIBE','DESCRIPTION','DESIGN','DESIRE','DESK','DESPITE','DESTROY','DETAIL','DETAILED','DETERMINE','DEVELOP','DEVELOPMENT','DEVICE','DIE','DIFFERENCE','DIFFERENT','DIFFICULT','DIFFICULTY','DINNER','DIRECT','DIRECTION','DIRECTLY','DIRECTOR','DISAPPEAR','DISCIPLINE','DISCOVER','DISCUSS','DISCUSSION','DISEASE','DISPLAY','DISTANCE','DISTINCTION','DISTRIBUTION','DISTRICT','DIVIDE','DIVISION','DO','DOCTOR','DOCUMENT','DOG','DOMESTIC','DOOR','DOUBLE','DOUBT','DOWN','DRAW','DRAWING','DREAM','DRESS','DRINK','DRIVE','DRIVER','DROP','DRUG','DRY','DUE','DURING','DUTY','EACH','EAR','EARLY','EARN','EARTH','EASILY','EAST','EASY','EAT','ECONOMIC','ECONOMY','EDGE','EDITOR','EDUCATION','EDUCATIONAL','EFFECT','EFFECTIVE','EFFECTIVELY','EFFORT','EGG','EITHER','ELDERLY','ELECTION','ELEMENT','ELSE','ELSEWHERE','EMERGE','EMPHASIS','EMPLOY','EMPLOYEE','EMPLOYER','EMPLOYMENT','EMPTY','ENABLE','ENCOURAGE','END','ENEMY','ENERGY','ENGINE','ENGINEERING','ENJOY','ENOUGH','ENSURE','ENTER','ENTERPRISE','ENTIRE','ENTIRELY','ENTITLE','ENTRY','ENVIRONMENT','ENVIRONMENTAL','EQUAL','EQUALLY','EQUIPMENT','ERROR','ESCAPE','ESPECIALLY','ESSENTIAL','ESTABLISH','ESTABLISHMENT','ESTATE','ESTIMATE','EVEN','EVENING','EVENT','EVENTUALLY','EVER','EVERY','EVERYBODY','EVERYONE','EVERYTHING','EVIDENCE','EXACTLY','EXAMINATION','EXAMINE','EXAMPLE','EXCELLENT','EXCEPT','EXCHANGE','EXECUTIVE','EXERCISE','EXHIBITION','EXIST','EXISTENCE','EXISTING','EXPECT','EXPECTATION','EXPENDITURE','EXPENSE','EXPENSIVE','EXPERIENCE','EXPERIMENT','EXPERT','EXPLAIN','EXPLANATION','EXPLORE','EXPRESS','EXPRESSION','EXTEND','EXTENT','EXTERNAL','EXTRA','EXTREMELY','EYE','FACE','FACILITY','FACT','FACTOR','FACTORY','FAIL','FAILURE','FAIR','FAIRLY','FAITH','FALL','FAMILIAR','FAMILY','FAMOUS','FAR','FARM','FARMER','FASHION','FAST','FATHER','FAVOUR','FEAR','FEATURE','FEE','FEEL','FEELING','FEMALE','FEW','FIELD','FIGHT','FIGURE','FILE','FILL','FILM','FINAL','FINALLY','FINANCE','FINANCIAL','FIND','FINDING','FINE','FINGER','FINISH','FIRE','FIRM','FIRST','FISH','FIT','FIX','FLAT','FLIGHT','FLOOR','FLOW','FLOWER','FLY','FOCUS','FOLLOW','FOLLOWING','FOOD','FOOT','FOOTBALL','FOR','FORCE','FOREIGN','FOREST','FORGET','FORM','FORMAL','FORMER','FORWARD','FOUNDATION','FREE','FREEDOM','FREQUENTLY','FRESH','FRIEND','FROM','FRONT','FRUIT','FUEL','FULL','FULLY','FUNCTION','FUND','FUNNY','FURTHER','FUTURE','GAIN','GAME','GARDEN','GAS','GATE','GATHER','GENERAL','GENERALLY','GENERATE','GENERATION','GENTLEMAN','GET','GIRL','GIVE','GLASS','GO','GOAL','GOD','GOLD','GOOD','GOVERNMENT','GRANT','GREAT','GREEN','GREY','GROUND','GROUP','GROW','GROWING','GROWTH','GUEST','GUIDE','GUN','HAIR','HALF','HALL','HAND','HANDLE','HANG','HAPPEN','HAPPY','HARD','HARDLY','HATE','HAVE','HE','HEAD','HEALTH','HEAR','HEART','HEAT','HEAVY','HELL','HELP','HENCE','HER','HERE','HERSELF','HIDE','HIGH','HIGHLY','HILL','HIM','HIMSELF','HIS','HISTORICAL','HISTORY','HIT','HOLD','HOLE','HOLIDAY','HOME','HOPE','HORSE','HOSPITAL','HOT','HOTEL','HOUR','HOUSE','HOUSEHOLD','HOUSING','HOW','HOWEVER','HUGE','HUMAN','HURT','HUSBAND','I','IDEA','IDENTIFY','IF','IGNORE','ILLUSTRATE','IMAGE','IMAGINE','IMMEDIATE','IMMEDIATELY','IMPACT','IMPLICATION','IMPLY','IMPORTANCE','IMPORTANT','IMPOSE','IMPOSSIBLE','IMPRESSION','IMPROVE','IMPROVEMENT','IN','INCIDENT','INCLUDE','INCLUDING','INCOME','INCREASE','INCREASED','INCREASINGLY','INDEED','INDEPENDENT','INDEX','INDICATE','INDIVIDUAL','INDUSTRIAL','INDUSTRY','INFLUENCE','INFORM','INFORMATION','INITIAL','INITIATIVE','INJURY','INSIDE','INSIST','INSTANCE','INSTEAD','INSTITUTE','INSTITUTION','INSTRUCTION','INSTRUMENT','INSURANCE','INTEND','INTENTION','INTEREST','INTERESTED','INTERESTING','INTERNAL','INTERNATIONAL','INTERPRETATION','INTERVIEW','INTO','INTRODUCE','INTRODUCTION','INVESTIGATE','INVESTIGATION','INVESTMENT','INVITE','INVOLVE','IRON','IS','ISLAND','ISSUE','IT','ITEM','ITS','ITSELF','JOB','JOIN','JOINT','JOURNEY','JUDGE','JUMP','JUST','JUSTICE','KEEP','KEY','KID','KILL','KIND','KING','KITCHEN','KNEE','KNOW','KNOWLEDGE','LABOUR','LACK','LADY','LAND','LANGUAGE','LARGE','LARGELY','LAST','LATE','LATER','LATTER','LAUGH','LAUNCH','LAW','LAWYER','LAY','LEAD','LEADER','LEADERSHIP','LEADING','LEAF','LEAGUE','LEAN','LEARN','LEAST','LEAVE','LEFT','LEG','LEGAL','LEGISLATION','LENGTH','LESS','LET','LETTER','LEVEL','LIABILITY','LIBERAL','LIBRARY','LIE','LIFE','LIFT','LIGHT','LIKE','LIKELY','LIMIT','LIMITED','LINE','LINK','LIP','LIST','LISTEN','LITERATURE','LITTLE','LIVE','LIVING','LOAN','LOCAL','LOCATION','LONG','LOOK','LORD','LOSE','LOSS','LOT','LOVE','LOVELY','LOW','LUNCH','MACHINE','MAGAZINE','MAIN','MAINLY','MAINTAIN','MAJOR','MAJORITY','MAKE','MALE','MAN','MANAGE','MANAGEMENT','MANAGER','MANNER','MANY','MAP','MARK','MARKET','MARRIAGE','MARRIED','MARRY','MASS','MASTER','MATCH','MATERIAL','MATTER','MAY','MAYBE','ME','MEAL','MEAN','MEANING','MEANS','MEANWHILE','MEASURE','MECHANISM','MEDIA','MEDICAL','MEET','MEETING','MEMBER','MEMBERSHIP','MEMORY','MENTAL','MENTION','MERELY','MESSAGE','METAL','METHOD','MIDDLE','MIGHT','MILE','MILITARY','MILK','MIND','MINE','MINISTER','MINISTRY','MINUTE','MISS','MISTAKE','MODEL','MODERN','MODULE','MOMENT','MONEY','MONTH','MORE','MORNING','MOST','MOTHER','MOTION','MOTOR','MOUNTAIN','MOUTH','MOVE','MOVEMENT','MUCH','MURDER','MUSEUM','MUSIC','MUST','MY','MYSELF','NAME','NARROW','NATION','NATIONAL','NATURAL','NATURE','NEAR','NEARLY','NECESSARILY','NECESSARY','NECK','NEED','NEGOTIATION','NEIGHBOUR','NEITHER','NETWORK','NEVER','NEVERTHELESS','NEW','NEWS','NEWSPAPER','NEXT','NICE','NIGHT','NO','NOBODY','NOD','NOISE','NONE','NOR','NORMAL','NORMALLY','NORTH','NORTHERN','NOSE','NOT','NOTE','NOTHING','NOTICE','NOTION','NOW','NUCLEAR','NUMBER','NURSE','OBJECT','OBJECTIVE','OBSERVATION','OBSERVE','OBTAIN','OBVIOUS','OBVIOUSLY','OCCASION','OCCUR','ODD','OF','OFF','OFFENCE','OFFER','OFFICE','OFFICER','OFFICIAL','OFTEN','OIL','OKAY','OLD','ON','ONCE','ONE','ONLY','ONTO','OPEN','OPERATE','OPERATION','OPINION','OPPORTUNITY','OPPOSITION','OPTION','OR','ORDER','ORDINARY','ORGANISATION','ORGANISE','ORGANIZATION','ORIGIN','ORIGINAL','OTHER','OTHERWISE','OUGHT','OUR','OURSELVES','OUT','OUTCOME','OUTPUT','OUTSIDE','OVER','OVERALL','OWN','OWNER','PACKAGE','PAGE','PAIN','PAINT','PAINTING','PAIR','PANEL','PAPER','PARENT','PARK','PARLIAMENT','PART','PARTICULAR','PARTICULARLY','PARTLY','PARTNER','PARTY','PASS','PASSAGE','PAST','PATH','PATIENT','PATTERN','PAY','PAYMENT','PEACE','PENSION','PEOPLE','PER','PERCENT','PERFECT','PERFORM','PERFORMANCE','PERHAPS','PERIOD','PERMANENT','PERSON','PERSONAL','PERSUADE','PHASE','PHONE','PHOTOGRAPH','PHYSICAL','PICK','PICTURE','PIECE','PLACE','PLAN','PLANNING','PLANT','PLASTIC','PLATE','PLAY','PLAYER','PLEASE','PLEASURE','PLENTY','PLUS','POCKET','POINT','POLICE','POLICY','POLITICAL','POLITICS','POOL','POOR','POPULAR','POPULATION','POSITION','POSITIVE','POSSIBILITY','POSSIBLE','POSSIBLY','POST','POTENTIAL','POUND','POWER','POWERFUL','PRACTICAL','PRACTICE','PREFER','PREPARE','PRESENCE','PRESENT','PRESIDENT','PRESS','PRESSURE','PRETTY','PREVENT','PREVIOUS','PREVIOUSLY','PRICE','PRIMARY','PRIME','PRINCIPLE','PRIORITY','PRISON','PRISONER','PRIVATE','PROBABLY','PROBLEM','PROCEDURE','PROCESS','PRODUCE','PRODUCT','PRODUCTION','PROFESSIONAL','PROFIT','PROGRAM','PROGRAMME','PROGRESS','PROJECT','PROMISE','PROMOTE','PROPER','PROPERLY','PROPERTY','PROPORTION','PROPOSE','PROPOSAL','PROSPECT','PROTECT','PROTECTION','PROVE','PROVIDE','PROVIDED','PROVISION','PUB','PUBLIC','PUBLICATION','PUBLISH','PULL','PUPIL','PURPOSE','PUSH','PUT','QUALITY','QUARTER','QUESTION','QUICK','QUICKLY','QUIET','QUITE','RACE','RADIO','RAILWAY','RAIN','RAISE','RANGE','RAPIDLY','RARE','RATE','RATHER','REACH','REACTION','READ','READER','READING','READY','REAL','REALISE','REALITY','REALIZE','REALLY','REASON','REASONABLE','RECALL','RECEIVE','RECENT','RECENTLY','RECOGNISE','RECOGNITION','RECOGNIZE','RECOMMEND','RECORD','RECOVER','RED','REDUCE','REDUCTION','REFER','REFERENCE','REFLECT','REFORM','REFUSE','REGARD','REGION','REGIONAL','REGULAR','REGULATION','REJECT','RELATE','RELATION','RELATIONSHIP','RELATIVE','RELATIVELY','RELEASE','RELEVANT','RELIEF','RELIGION','RELIGIOUS','RELY','REMAIN','REMEMBER','REMIND','REMOVE','REPEAT','REPLACE','REPLY','REPORT','REPRESENT','REPRESENTATION','REPRESENTATIVE','REQUEST','REQUIRE','REQUIREMENT','RESEARCH','RESOURCE','RESPECT','RESPOND','RESPONSE','RESPONSIBILITY','RESPONSIBLE','REST','RESTAURANT','RESULT','RETAIN','RETURN','REVEAL','REVENUE','REVIEW','REVOLUTION','RICH','RIDE','RIGHT','RING','RISE','RISK','RIVER','ROAD','ROCK','ROLE','ROLL','ROOF','ROOM','ROUND','ROUTE','ROW','ROYAL','RULE','RUN','RURAL','SAFE','SAFETY','SALE','SAME','SAMPLE','SATISFY','SAVE','SAY','SCALE','SCENE','SCHEME','SCHOOL','SCIENCE','SCIENTIFIC','SCIENTIST','SCORE','SCREEN','SEA','SEARCH','SEASON','SEAT','SECOND','SECONDARY','SECRETARY','SECTION','SECTOR','SECURE','SECURITY','SEE','SEEK','SEEM','SELECT','SELECTION','SELL','SEND','SENIOR','SENSE','SENTENCE','SEPARATE','SEQUENCE','SERIES','SERIOUS','SERIOUSLY','SERVANT','SERVE','SERVICE','SESSION','SET','SETTLE','SETTLEMENT','SEVERAL','SEVERE','SEX','SEXUAL','SHAKE','SHALL','SHAPE','SHARE','SHE','SHEET','SHIP','SHOE','SHOOT','SHOP','SHORT','SHOT','SHOULD','SHOULDER','SHOUT','SHOW','SHUT','SIDE','SIGHT','SIGN','SIGNAL','SIGNIFICANCE','SIGNIFICANT','SILENCE','SIMILAR','SIMPLE','SIMPLY','SINCE','SING','SINGLE','SIR','SISTER','SIT','SITE','SITUATION','SIZE','SKILL','SKIN','SKY','SLEEP','SLIGHTLY','SLIP','SLOW','SLOWLY','SMALL','SMILE','SO','SOCIAL','SOCIETY','SOFT','SOFTWARE','SOIL','SOLDIER','SOLICITOR','SOLUTION','SOME','SOMEBODY','SOMEONE','SOMETHING','SOMETIMES','SOMEWHAT','SOMEWHERE','SON','SONG','SOON','SORRY','SORT','SOUND','SOURCE','SOUTH','SOUTHERN','SPACE','SPEAK','SPEAKER','SPECIAL','SPECIES','SPECIFIC','SPEECH','SPEED','SPEND','SPIRIT','SPORT','SPOT','SPREAD','SPRING','STAFF','STAGE','STAND','STANDARD','STAR','START','STATE','STATEMENT','STATION','STATUS','STAY','STEAL','STEP','STICK','STILL','STOCK','STONE','STOP','STORE','STORY','STRAIGHT','STRANGE','STRATEGY','STREET','STRENGTH','STRIKE','STRONG','STRONGLY','STRUCTURE','STUDENT','STUDIO','STUDY','STUFF','STYLE','SUBJECT','SUBSTANTIAL','SUCCEED','SUCCESS','SUCCESSFUL','SUCH','SUDDENLY','SUFFER','SUFFICIENT','SUGGEST','SUGGESTION','SUITABLE','SUM','SUMMER','SUN','SUPPLY','SUPPORT','SUPPOSE','SURE','SURELY','SURFACE','SURPRISE','SURROUND','SURVEY','SURVIVE','SWITCH','SYSTEM','TABLE','TAKE','TALK','TALL','TAPE','TARGET','TASK','TAX','TEA','TEACH','TEACHER','TEACHING','TEAM','TEAR','TECHNICAL','TECHNIQUE','TECHNOLOGY','TELEPHONE','TELEVISION','TELL','TEMPERATURE','TEND','TERM','TERMS','TERRIBLE','TEST','TEXT','THAN','THANK','THANKS','THAT','THE','THEATRE','THEIR','THEM','THEME','THEMSELVES','THEN','THEORY','THERE','THEREFORE','THESE','THEY','THIN','THING','THINK','THIS','THOSE','THOUGH','THOUGHT','THREAT','THREATEN','THROUGH','THROUGHOUT','THROW','THUS','TICKET','TIME','TINY','TITLE','TO','TODAY','TOGETHER','TOMORROW','TONE','TONIGHT','TOO','TOOL','TOOTH','TOP','TOTAL','TOTALLY','TOUCH','TOUR','TOWARDS','TOWN','TRACK','TRADE','TRADITION','TRADITIONAL','TRAFFIC','TRAIN','TRAINING','TRANSFER','TRANSPORT','TRAVEL','TREAT','TREATMENT','TREATY','TREE','TREND','TRIAL','TRIP','TROOP','TROUBLE','TRUE','TRUST','TRUTH','TRY','TURN','TWICE','TYPE','TYPICAL','UNABLE','UNDER','UNDERSTAND','UNDERSTANDING','UNDERTAKE','UNEMPLOYMENT','UNFORTUNATELY','UNION','UNIT','UNITED','UNIVERSITY','UNLESS','UNLIKELY','UNTIL','UP','UPON','UPPER','URBAN','US','USE','USED','USEFUL','USER','USUAL','USUALLY','VALUE','VARIATION','VARIETY','VARIOUS','VARY','VAST','VEHICLE','VERSION','VERY','VIA','VICTIM','VICTORY','VIDEO','VIEW','VILLAGE','VIOLENCE','VISION','VISIT','VISITOR','VITAL','VOICE','VOLUME','VOTE','WAGE','WAIT','WALK','WALL','WANT','WAR','WARM','WARN','WASH','WATCH','WATER','WAVE','WAY','WE','WEAK','WEAPON','WEAR','WEATHER','WEEK','WEEKEND','WEIGHT','WELCOME','WELFARE','WELL','WEST','WESTERN','WHAT','WHATEVER','WHEN','WHERE','WHEREAS','WHETHER','WHICH','WHILE','WHILST','WHITE','WHO','WHOLE','WHOM','WHOSE','WHY','WIDE','WIDELY','WIFE','WILD','WILL','WIN','WIND','WINDOW','WINE','WING','WINNER','WINTER','WISH','WITH','WITHDRAW','WITHIN','WITHOUT','WOMAN','WONDER','WONDERFUL','WOOD','WORD','WORK','WORKER','WORKING','WORKS','WORLD','WORRY','WORTH','WOULD','WRITE','WRITER','WRITING','WRONG','YARD','YEAH','YEAR','YES','YESTERDAY','YET','YOU','YOUNG','YOUR','YOURSELF','YOUTH'];
+
+codedTriangleNumbers(1786);
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-43-sub-string-divisibility.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-43-sub-string-divisibility.md
new file mode 100644
index 00000000000..53ae7b50350
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-43-sub-string-divisibility.md
@@ -0,0 +1,126 @@
+---
+id: 5900f3971000cf542c50feaa
+title: 'Problem 43: Sub-string divisibility'
+challengeType: 1
+forumTopicId: 302100
+dashedName: problem-43-sub-string-divisibility
+---
+
+# --description--
+
+The number, 1406357289, is a 0 to 9 pandigital number because it is made up of each of the digits 0 to 9 in some order, but it also has a rather interesting sub-string divisibility property.
+
+Let $d_1$ be the $1^{st}$ digit, $d_2$ be the $2^{nd}$ digit, and so on. In this way, we note the following:
+
+- ${d_2}{d_3}{d_4} = 406$ is divisible by 2
+- ${d_3}{d_4}{d_5} = 063$ is divisible by 3
+- ${d_4}{d_5}{d_6} = 635$ is divisible by 5
+- ${d_5}{d_6}{d_7} = 357$ is divisible by 7
+- ${d_6}{d_7}{d_8} = 572$ is divisible by 11
+- ${d_7}{d_8}{d_9} = 728$ is divisible by 13
+- ${d_8}{d_9}{d_{10}} = 289$ is divisible by 17
+
+Find the sum of all 0 to `n` pandigital numbers with sub-strings fulfilling `n - 2` of these divisibility properties.
+
+**Note:** Pandigital numbers starting with `0` are to be considered in the result.
+
+# --hints--
+
+`substringDivisibility(5)` should return a number.
+
+```js
+assert(typeof substringDivisibility(5) === 'number');
+```
+
+`substringDivisibility(5)` should return `12444480`.
+
+```js
+assert.strictEqual(substringDivisibility(5), 12444480)
+```
+
+`substringDivisibility(7)` should return `1099210170`.
+
+```js
+assert.strictEqual(substringDivisibility(7), 1099210170)
+```
+
+`substringDivisibility(8)` should return `1113342912`.
+
+```js
+assert.strictEqual(substringDivisibility(8), 1113342912)
+```
+
+`substringDivisibility(9)` should return `16695334890`.
+
+```js
+assert.strictEqual(substringDivisibility(9), 16695334890)
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function substringDivisibility(n) {
+
+ return true;
+}
+
+substringDivisibility(5);
+```
+
+# --solutions--
+
+```js
+function substringDivisibility(n) {
+ function isSubDivisable(digits) {
+ const factors = [2, 3, 5, 7, 11, 13, 17];
+
+ for (let i = 1; i < digits.length - 2; i++) {
+ const subNumber = digits[i] * 100 + digits[i + 1] * 10 + digits[i + 2];
+ if (subNumber % factors[i - 1] !== 0) {
+ return false;
+ }
+ }
+ return true;
+ }
+
+ function heapsPermutations(k, digits, conditionCheck, results) {
+ if (k === 1) {
+ if (conditionCheck(digits)) {
+ const number = parseInt(digits.join(''), 10);
+ results.push(number);
+ }
+ return;
+ }
+
+ heapsPermutations(k - 1, digits, conditionCheck, results);
+
+ for (let i = 0; i < k - 1; i++) {
+ if (k % 2 === 0) {
+ [digits[i], digits[k - 1]] = [digits[k - 1], digits[i]];
+ } else {
+ [digits[0], digits[k - 1]] = [digits[k - 1], digits[0]];
+ }
+ heapsPermutations(k - 1, digits, conditionCheck, results);
+ }
+ return;
+ }
+
+ const allowedDigits = [...new Array(n + 1).keys()];
+ const divisablePandigitals = [];
+ heapsPermutations(
+ allowedDigits.length,
+ allowedDigits,
+ isSubDivisable,
+ divisablePandigitals
+ );
+
+ let sum = 0;
+ for (let i = 0; i < divisablePandigitals.length; i++) {
+ sum += divisablePandigitals[i];
+ }
+
+ return sum;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-44-pentagon-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-44-pentagon-numbers.md
new file mode 100644
index 00000000000..44905c1be79
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-44-pentagon-numbers.md
@@ -0,0 +1,77 @@
+---
+id: 5900f3981000cf542c50feab
+title: 'Problem 44: Pentagon numbers'
+challengeType: 1
+forumTopicId: 302111
+dashedName: problem-44-pentagon-numbers
+---
+
+# --description--
+
+Pentagonal numbers are generated by the formula, Pn=`n`(3`n`−1)/2. The first ten pentagonal numbers are:
+
+1, 5, 12, 22, 35, 51, 70, 92, 117, 145, ...
+
+It can be seen that P4 + P7 = 22 + 70 = 92 = P8. However, their difference, 70 − 22 = 48, is not pentagonal.
+
+Find the pair of pentagonal numbers, Pj and Pk, for which their sum and difference are pentagonal and D = |Pk − Pj| is minimized; what is the value of D?
+
+# --hints--
+
+`pentagonNumbers()` should return a number.
+
+```js
+assert(typeof pentagonNumbers() === 'number');
+```
+
+`pentagonNumbers()` should return 5482660.
+
+```js
+assert.strictEqual(pentagonNumbers(), 5482660);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pentagonNumbers() {
+
+ return true;
+}
+
+pentagonNumbers();
+```
+
+# --solutions--
+
+```js
+function pentagonNumbers() {
+ function isPentagonal(num) {
+ // Formula found by solving pentagonal number
+ // equation for n.
+ const n = (Math.sqrt((24 * num) + 1) + 1) / 6;
+ return n % 1 === 0;
+ }
+
+ function pentagonal(num) {
+ return (num * ((3 * num) - 1)) / 2;
+ }
+ let result;
+ let i = 1;
+ while (!result) {
+ i++;
+ const num1 = (i * ((3 * i) - 1)) / 2; // Pentagonal num formula
+ const minDiff = num1 - (((i - 1) * ((3 * (i - 1)) - 1)) / 2);
+ let j = i - 1;
+ while (j > 0 && !result) {
+ const num2 = (j * ((3 * j) - 1)) / 2;
+ if (isPentagonal(num1 - num2) && isPentagonal(num1 + num2)) {
+ result = num1 - num2;
+ }
+ j--;
+ }
+ }
+ return result;
+ }
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-45-triangular-pentagonal-and-hexagonal.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-45-triangular-pentagonal-and-hexagonal.md
new file mode 100644
index 00000000000..e80bcc8dd50
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-45-triangular-pentagonal-and-hexagonal.md
@@ -0,0 +1,82 @@
+---
+id: 5900f3991000cf542c50feac
+title: 'Problem 45: Triangular, pentagonal, and hexagonal'
+challengeType: 1
+forumTopicId: 302122
+dashedName: problem-45-triangular-pentagonal-and-hexagonal
+---
+
+# --description--
+
+Triangle, pentagonal, and hexagonal numbers are generated by the following formulae:
+
+Triangle
Tn=n(n+1)/2
1, 3, 6, 10, 15, ...
Pentagonal
Pn=n(3n−1)/2
1, 5, 12, 22, 35, ...
Hexagonal
Hn=n(2n−1)
1, 6, 15, 28, 45, ...
+ 9 = 7 + 2×12
+ 15 = 7 + 2×22
+ 21 = 3 + 2×32
+ 25 = 7 + 2×32
+ 27 = 19 + 2×22
+ 33 = 31 + 2×12 +
+
+It turns out that the conjecture was false.
+
+What is the smallest odd composite that cannot be written as the sum of a prime and twice a square?
+
+# --hints--
+
+`goldbachsOtherConjecture()` should return a number.
+
+```js
+assert(typeof goldbachsOtherConjecture() === 'number');
+```
+
+`goldbachsOtherConjecture()` should return 5777.
+
+```js
+assert.strictEqual(goldbachsOtherConjecture(), 5777);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function goldbachsOtherConjecture() {
+
+ return true;
+}
+
+goldbachsOtherConjecture();
+```
+
+# --solutions--
+
+```js
+function goldbachsOtherConjecture() { function isPrime(num) {
+ if (num < 2) {
+ return false;
+ } else if (num === 2) {
+ return true;
+ }
+ const sqrtOfNum = Math.floor(num ** 0.5);
+ for (let i = 2; i <= sqrtOfNum + 1; i++) {
+ if (num % i === 0) {
+ return false;
+ }
+ }
+ return true;
+ }
+
+ function isSquare(num) {
+ return Math.sqrt(num) % 1 === 0;
+ }
+
+ // construct a list of prime numbers
+ const primes = [];
+ for (let i = 2; primes.length < 1000; i++) {
+ if (isPrime(i)) primes.push(i);
+ }
+
+ let num = 3;
+ let answer;
+ while (!answer) {
+ num += 2;
+ if (!isPrime(num)) {
+ let found = false;
+ for (let primeI = 0; primeI < primes.length && !found; primeI++) {
+ const square = (num - primes[primeI]) / 2;
+ if (isSquare(square)) {
+ found = true;
+ break;
+ }
+ }
+ if (!found) answer = num;
+ }
+ }
+ return answer;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-47-distinct-primes-factors.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-47-distinct-primes-factors.md
new file mode 100644
index 00000000000..3b79403a4ea
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-47-distinct-primes-factors.md
@@ -0,0 +1,94 @@
+---
+id: 5900f39c1000cf542c50feae
+title: 'Problem 47: Distinct primes factors'
+challengeType: 1
+forumTopicId: 302145
+dashedName: problem-47-distinct-primes-factors
+---
+
+# --description--
+
+The first two consecutive numbers to have two distinct prime factors are:
+
++ 15 = 7 + 2×22
+ 21 = 3 + 2×32
+ 25 = 7 + 2×32
+ 27 = 19 + 2×22
+ 33 = 31 + 2×12 +
+ 14 = 2 × 7
+ 15 = 3 × 5 +
+
+The first three consecutive numbers to have three distinct prime factors are:
+
++ 15 = 3 × 5 +
+ 644 = 22 × 7 × 23
+ 645 = 3 × 5 × 43
+ 646 = 2 × 17 × 19 +
+
+Find the first four consecutive integers to have four distinct prime factors each. What is the first of these numbers?
+
+# --hints--
+
+`distinctPrimeFactors(2, 2)` should return a number.
+
+```js
+assert(typeof distinctPrimeFactors(2, 2) === 'number');
+```
+
+`distinctPrimeFactors(2, 2)` should return 14.
+
+```js
+assert.strictEqual(distinctPrimeFactors(2, 2), 14);
+```
+
+`distinctPrimeFactors(3, 3)` should return 644.
+
+```js
+assert.strictEqual(distinctPrimeFactors(3, 3), 644);
+```
+
+`distinctPrimeFactors(4, 4)` should return 134043.
+
+```js
+assert.strictEqual(distinctPrimeFactors(4, 4), 134043);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function distinctPrimeFactors(targetNumPrimes, targetConsecutive) {
+
+ return true;
+}
+
+distinctPrimeFactors(4, 4);
+```
+
+# --solutions--
+
+```js
+function distinctPrimeFactors(targetNumPrimes, targetConsecutive) {
+ const primeLimit = targetNumPrimes * targetConsecutive * 10000;
+ const numFactors = Array(primeLimit).fill(0);
+
+ let numConsecutive = 0;
+ for (let i = 2; i < primeLimit; i++) {
+ if (numFactors[i] === targetNumPrimes) {
+ // Current number is composite with target num factors
+ numConsecutive++;
+ if (numConsecutive === targetConsecutive) {
+ return i - numConsecutive + 1;
+ }
+ } else {
+ // Current number is not matching composite
+ numConsecutive = 0;
+ if (numFactors[i] === 0) {
+ // Current number is prime
+ for (let j = i; j < primeLimit; j += i) {
+ numFactors[j]++;
+ }
+ }
+ }
+ }
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-48-self-powers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-48-self-powers.md
new file mode 100644
index 00000000000..d429c978791
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-48-self-powers.md
@@ -0,0 +1,80 @@
+---
+id: 5900f39c1000cf542c50feaf
+title: 'Problem 48: Self powers'
+challengeType: 1
+forumTopicId: 302157
+dashedName: problem-48-self-powers
+---
+
+# --description--
+
+The series, 11 + 22 + 33 + ... + 1010 = 10405071317.
+
+Find the last ten digits of the series, 11 + 22 + 33 + ... + 10001000.
+
+# --hints--
+
+`selfPowers(10, 3)` should return a number.
+
+```js
+assert(typeof selfPowers(10, 3) === 'number');
+```
+
+`selfPowers(10, 3)` should return 317.
+
+```js
+assert.strictEqual(selfPowers(10, 3), 317);
+```
+
+`selfPowers(150, 6)` should return 29045.
+
+```js
+assert.strictEqual(selfPowers(150, 6), 29045);
+```
+
+`selfPowers(673, 7)` should return 2473989.
+
+```js
+assert.strictEqual(selfPowers(673, 7), 2473989);
+```
+
+`selfPowers(1000, 10)` should return 9110846700.
+
+```js
+assert.strictEqual(selfPowers(1000, 10), 9110846700);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function selfPowers(power, lastDigits) {
+
+ return true;
+}
+
+selfPowers(1000, 10);
+```
+
+# --solutions--
+
+```js
+function selfPowers(power, lastDigits) {
+ let sum = 0;
+ const modulo = Math.pow(10, lastDigits);
+
+ for (let i = 1; i <= power; i++) {
+ let temp = i;
+ for (let j = 1; j < i; j++) {
+ temp *= i;
+ temp %= modulo;
+ }
+
+ sum += temp;
+ sum %= modulo;
+ }
+
+ return sum;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-49-prime-permutations.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-49-prime-permutations.md
new file mode 100644
index 00000000000..3c0c1d3d362
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-49-prime-permutations.md
@@ -0,0 +1,93 @@
+---
+id: 5900f39d1000cf542c50feb0
+title: 'Problem 49: Prime permutations'
+challengeType: 1
+forumTopicId: 302159
+dashedName: problem-49-prime-permutations
+---
+
+# --description--
+
+The arithmetic sequence, 1487, 4817, 8147, in which each of the terms increases by 3330, is unusual in two ways: (i) each of the three terms are prime, and, (ii) each of the 4-digit numbers are permutations of one another.
+
+There are no arithmetic sequences made up of three 1-, 2-, or 3-digit primes, exhibiting this property, but there is one other 4-digit increasing sequence.
+
+What 12-digit number do you form by concatenating the three terms in this sequence?
+
+# --hints--
+
+`primePermutations()` should return a number.
+
+```js
+assert(typeof primePermutations() === 'number');
+```
+
+`primePermutations()` should return 296962999629.
+
+```js
+assert.strictEqual(primePermutations(), 296962999629);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primePermutations() {
+
+ return true;
+}
+
+primePermutations();
+```
+
+# --solutions--
+
+```js
+function primePermutations() {
+ function arePermutations(num1, num2) {
+ const numStr1 = num1.toString();
+ let numStr2 = num2.toString();
+ if (numStr1.length !== numStr2.length) {
+ return false;
+ }
+
+ for (let i = 0; i < numStr1.length; i++) {
+ const index = numStr2.indexOf(numStr1[i]);
+ if (index === -1) {
+ return false;
+ }
+ numStr2 = numStr2.slice(0, index) + numStr2.slice(index + 1);
+ }
+ return true;
+ }
+
+ function isPrime(num) {
+ if (num < 2) {
+ return false;
+ } else if (num === 2) {
+ return true;
+ }
+ const sqrtOfNum = Math.floor(num ** 0.5);
+ for (let i = 2; i <= sqrtOfNum + 1; i++) {
+ if (num % i === 0) {
+ return false;
+ }
+ }
+ return true;
+ }
+
+ for (let num1 = 1000; num1 <= 9999; num1++) {
+ const num2 = num1 + 3330;
+ const num3 = num2 + 3330;
+ if (isPrime(num1) && isPrime(num2) && isPrime(num3)) {
+ if (arePermutations(num1, num2) && arePermutations(num1, num3)
+ && num1 !== 1487) {
+ // concatenate and return numbers
+ return (num1 * 100000000) + (num2 * 10000) + num3;
+ }
+ }
+ }
+ return 0;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-5-smallest-multiple.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-5-smallest-multiple.md
new file mode 100644
index 00000000000..2f20bceaadf
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-5-smallest-multiple.md
@@ -0,0 +1,83 @@
+---
+id: 5900f3711000cf542c50fe84
+title: 'Problem 5: Smallest multiple'
+challengeType: 1
+forumTopicId: 302160
+dashedName: problem-5-smallest-multiple
+---
+
+# --description--
+
+2520 is the smallest number that can be divided by each of the numbers from 1 to 10 without any remainder.
+
+What is the smallest positive number that is evenly divisible by all of the numbers from 1 to `n`?
+
+# --hints--
+
+`smallestMult(5)` should return a number.
+
+```js
+assert(typeof smallestMult(5) === 'number');
+```
+
+`smallestMult(5)` should return 60.
+
+```js
+assert.strictEqual(smallestMult(5), 60);
+```
+
+`smallestMult(7)` should return 420.
+
+```js
+assert.strictEqual(smallestMult(7), 420);
+```
+
+`smallestMult(10)` should return 2520.
+
+```js
+assert.strictEqual(smallestMult(10), 2520);
+```
+
+`smallestMult(13)` should return 360360.
+
+```js
+assert.strictEqual(smallestMult(13), 360360);
+```
+
+`smallestMult(20)` should return 232792560.
+
+```js
+assert.strictEqual(smallestMult(20), 232792560);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function smallestMult(n) {
+
+ return true;
+}
+
+smallestMult(20);
+```
+
+# --solutions--
+
+```js
+function smallestMult(n){
+ function gcd(a, b) {
+ return b === 0 ? a : gcd(b, a%b); // Euclidean algorithm
+ }
+
+ function lcm(a, b) {
+ return a * b / gcd(a, b);
+ }
+ var result = 1;
+ for(var i = 2; i <= n; i++) {
+ result = lcm(result, i);
+ }
+ return result;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-50-consecutive-prime-sum.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-50-consecutive-prime-sum.md
new file mode 100644
index 00000000000..7cd5bc67b14
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-50-consecutive-prime-sum.md
@@ -0,0 +1,139 @@
+---
+id: 5900f39e1000cf542c50feb1
+title: 'Problem 50: Consecutive prime sum'
+challengeType: 1
+forumTopicId: 302161
+dashedName: problem-50-consecutive-prime-sum
+---
+
+# --description--
+
+The prime 41, can be written as the sum of six consecutive primes:
+
++ 645 = 3 × 5 × 43
+ 646 = 2 × 17 × 19 +
41 = 2 + 3 + 5 + 7 + 11 + 13
+
+This is the longest sum of consecutive primes that adds to a prime below one-hundred.
+
+The longest sum of consecutive primes below one-thousand that adds to a prime, contains 21 terms, and is equal to 953.
+
+Which prime, below one-million, can be written as the sum of the most consecutive primes?
+
+# --hints--
+
+`consecutivePrimeSum(1000)` should return a number.
+
+```js
+assert(typeof consecutivePrimeSum(1000) === 'number');
+```
+
+`consecutivePrimeSum(1000)` should return 953.
+
+```js
+assert.strictEqual(consecutivePrimeSum(1000), 953);
+```
+
+`consecutivePrimeSum(1000000)` should return 997651.
+
+```js
+assert.strictEqual(consecutivePrimeSum(1000000), 997651);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function consecutivePrimeSum(limit) {
+
+ return true;
+}
+
+consecutivePrimeSum(1000000);
+```
+
+# --solutions--
+
+```js
+class PrimeSeive {
+ constructor(num) {
+ const seive = Array(Math.floor((num - 1) / 2)).fill(true);
+ const primes = [2];
+ const upper = Math.floor((num - 1) / 2);
+ const sqrtUpper = Math.floor((Math.sqrt(num) - 1) / 2);
+
+ for (let i = 0; i <= sqrtUpper; i++) {
+ if (seive[i]) {
+ // Mark value in seive array
+ const prime = 2 * i + 3;
+ primes.push(prime);
+ // Mark all multiples of this number as false (not prime)
+ const primeSqaredIndex = 2 * i ** 2 + 6 * i + 3;
+ for (let j = primeSqaredIndex; j < upper; j += prime) {
+ seive[j] = false;
+ }
+ }
+ }
+ for (let i = sqrtUpper + 1; i < upper; i++) {
+ if (seive[i]) {
+ primes.push(2 * i + 3);
+ }
+ }
+
+ this._seive = seive;
+ this._primes = primes;
+ }
+
+ isPrime(num) {
+ return num === 2
+ ? true
+ : num % 2 === 0
+ ? false
+ : this.isOddPrime(num);
+ }
+
+ isOddPrime(num) {
+ return this._seive[(num - 3) / 2];
+ }
+
+ get primes() {
+ return this._primes;
+ }
+};
+
+function consecutivePrimeSum(limit) {
+ // Initalize seive
+ const primeSeive = new PrimeSeive(limit);
+
+ // Initalize for longest sum < 100
+ let bestPrime = 41;
+ let bestI = 0;
+ let bestJ = 5;
+
+ // Find longest sum < limit
+ let sumOfCurrRange = 41;
+ let i = 0, j = 5;
+ // -- Loop while current some starting at i is < limit
+ while (sumOfCurrRange < limit) {
+ let currSum = sumOfCurrRange;
+ // -- Loop while pushing j towards end of PRIMES list
+ // keeping sum under limit
+ while (currSum < limit) {
+ if (primeSeive.isPrime(currSum)) {
+ bestPrime = sumOfCurrRange = currSum;
+ bestI = i;
+ bestJ = j;
+ }
+ // -- Increment inner loop
+ j++;
+ currSum += primeSeive.primes[j];
+ }
+ // -- Increment outer loop
+ i++;
+ j = i + (bestJ - bestI);
+ sumOfCurrRange -= primeSeive.primes[i - 1];
+ sumOfCurrRange += primeSeive.primes[j];
+ }
+ // Return
+ return bestPrime;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-51-prime-digit-replacements.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-51-prime-digit-replacements.md
new file mode 100644
index 00000000000..cdbfc3e568b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-51-prime-digit-replacements.md
@@ -0,0 +1,140 @@
+---
+id: 5900f39f1000cf542c50feb2
+title: 'Problem 51: Prime digit replacements'
+challengeType: 1
+forumTopicId: 302162
+dashedName: problem-51-prime-digit-replacements
+---
+
+# --description--
+
+By replacing the 1st digit of the 2-digit number \*3, it turns out that six of the nine possible values: 13, 23, 43, 53, 73, and 83, are all prime.
+
+By replacing the 3rd and 4th digits of 56\*\*3 with the same digit, this 5-digit number is the first example having seven primes among the ten generated numbers, yielding the family: 56003, 56113, 56333, 56443, 56663, 56773, and 56993. Consequently 56003, being the first member of this family, is the smallest prime with this property.
+
+Find the smallest prime which, by replacing part of the number (not necessarily adjacent digits) with the same digit, is part of an `n` prime value family.
+
+# --hints--
+
+`primeDigitReplacements(6)` should return a number.
+
+```js
+assert(typeof primeDigitReplacements(6) === 'number');
+```
+
+`primeDigitReplacements(6)` should return `13`.
+
+```js
+assert.strictEqual(primeDigitReplacements(6), 13);
+```
+
+`primeDigitReplacements(7)` should return `56003`.
+
+```js
+assert.strictEqual(primeDigitReplacements(7), 56003);
+```
+
+`primeDigitReplacements(8)` should return `121313`.
+
+```js
+assert.strictEqual(primeDigitReplacements(8), 121313);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeDigitReplacements(n) {
+
+ return true;
+}
+
+primeDigitReplacements(6);
+```
+
+# --solutions--
+
+```js
+class PrimeSeive {
+ constructor(num) {
+ const seive = Array(Math.floor((num - 1) / 2)).fill(true);
+ const upper = Math.floor((num - 1) / 2);
+ const sqrtUpper = Math.floor((Math.sqrt(num) - 1) / 2);
+
+ for (let i = 0; i <= sqrtUpper; i++) {
+ if (seive[i]) {
+ // Mark value in seive array
+ const prime = 2 * i + 3;
+ // Mark all multiples of this number as false (not prime)
+ const primeSqaredIndex = 2 * i ** 2 + 6 * i + 3;
+ for (let j = primeSqaredIndex; j < upper; j += prime) {
+ seive[j] = false;
+ }
+ }
+ }
+
+ this._seive = seive;
+ }
+
+ isPrime(num) {
+ return num === 2
+ ? true
+ : num % 2 === 0
+ ? false
+ : this.isOddPrime(num);
+ }
+
+ isOddPrime(num) {
+ return this._seive[(num - 3) / 2];
+ }
+};
+
+function primeDigitReplacements(n) {
+ const primeSeive = new PrimeSeive(n * n * n * 2000);
+
+ function isNFamily(number, n) {
+ const prime = number.toString();
+ const lastDigit = prime[prime.length - 1];
+ return doesReplacingMakeFamily(prime, '0', n) ||
+ doesReplacingMakeFamily(prime, '2', n) ||
+ (lastDigit !== '1' && doesReplacingMakeFamily(prime, '1', n));
+ }
+
+ function doesReplacingMakeFamily(prime, digitToReplace, family) {
+ let miss = 0;
+ const base = parseInt(
+ prime
+ .split('')
+ .map(digit => digit == digitToReplace ? '0' : digit)
+ .join('')
+ );
+ const replacements = parseInt(
+ prime
+ .split('')
+ .map(digit => digit === digitToReplace ? '1' : '0')
+ .join('')
+ );
+ const start = prime[0] === digitToReplace ? 1 : 0;
+ for (let i = start; i < 10; i++) {
+ const nextNumber = base + i * replacements;
+ if (!isPartOfFamily(nextNumber, prime)) miss++;
+ if (10 - start - miss < family) break;
+ }
+ return 10 - start - miss === family;
+ }
+
+ function isPartOfFamily(number, prime) {
+ return (
+ primeSeive.isPrime(number) && number.toString().length === prime.length
+ );
+ }
+
+ for (let number = 1; number < 125000; number++) {
+ if (primeSeive.isPrime(number) && isNFamily(number, n)) {
+ return number;
+ }
+ }
+ return -1;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-52-permuted-multiples.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-52-permuted-multiples.md
new file mode 100644
index 00000000000..7a3886a6e27
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-52-permuted-multiples.md
@@ -0,0 +1,81 @@
+---
+id: 5900f3a01000cf542c50feb3
+title: 'Problem 52: Permuted multiples'
+challengeType: 1
+forumTopicId: 302163
+dashedName: problem-52-permuted-multiples
+---
+
+# --description--
+
+It can be seen that the number, 125874, and its double, 251748, contain exactly the same digits, but in a different order.
+
+Find the smallest positive integer, such that multiplied by integers $\\{2, 3, \ldots, n\\}$, contain the same digits.
+
+# --hints--
+
+`permutedMultiples(2)` should return a number.
+
+```js
+assert(typeof permutedMultiples(2) === 'number');
+```
+
+`permutedMultiples(2)` should return `125874`.
+
+```js
+assert.strictEqual(permutedMultiples(2), 125874);
+```
+
+`permutedMultiples(6)` should return `142857`.
+
+```js
+assert.strictEqual(permutedMultiples(6), 142857);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function permutedMultiples(n) {
+
+ return true;
+}
+
+permutedMultiples(2);
+```
+
+# --solutions--
+
+```js
+function permutedMultiples(n) {
+ const isPermutation = (a, b) =>
+ a.length !== b.length
+ ? false
+ : a.split('').sort().join() === b.split('').sort().join();
+
+
+ let start = 1;
+ let found = false;
+ let result = 0;
+
+ while (!found) {
+ start *= 10;
+ for (let i = start; i < start * 10 / n; i++) {
+ found = true;
+ for (let j = 2; j <= n; j++) {
+ if (!isPermutation(i + '', j * i + '')) {
+ found = false;
+ break;
+ }
+ }
+ if (found) {
+ result = i;
+ break;
+ }
+ }
+ }
+
+ return result;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-53-combinatoric-selections.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-53-combinatoric-selections.md
new file mode 100644
index 00000000000..8d96ff14392
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-53-combinatoric-selections.md
@@ -0,0 +1,89 @@
+---
+id: 5900f3a11000cf542c50feb4
+title: 'Problem 53: Combinatoric selections'
+challengeType: 1
+forumTopicId: 302164
+dashedName: problem-53-combinatoric-selections
+---
+
+# --description--
+
+There are exactly ten ways of selecting three from five, 12345:
+
+123, 124, 125, 134, 135, 145, 234, 235, 245, and 345
+
+In combinatorics, we use the notation, $\\displaystyle \\binom 5 3 = 10$
+
+In general, $\\displaystyle \\binom n r = \\dfrac{n!}{r!(n-r)!}$, where $r \\le n$, $n! = n \\times (n-1) \\times ... \\times 3 \\times 2 \\times 1$, and $0! = 1$.
+
+It is not until $n = 23$, that a value exceeds one-million: $\\displaystyle \\binom {23} {10} = 1144066$.
+
+How many, not necessarily distinct, values of $\\displaystyle \\binom n r$ for $1 \\le n \\le 100$, are greater than one-million?
+
+# --hints--
+
+`combinatoricSelections(1000)` should return a number.
+
+```js
+assert(typeof combinatoricSelections(1000) === 'number');
+```
+
+`combinatoricSelections(1000)` should return 4626.
+
+```js
+assert.strictEqual(combinatoricSelections(1000), 4626);
+```
+
+`combinatoricSelections(10000)` should return 4431.
+
+```js
+assert.strictEqual(combinatoricSelections(10000), 4431);
+```
+
+`combinatoricSelections(100000)` should return 4255.
+
+```js
+assert.strictEqual(combinatoricSelections(100000), 4255);
+```
+
+`combinatoricSelections(1000000)` should return 4075.
+
+```js
+assert.strictEqual(combinatoricSelections(1000000), 4075);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function combinatoricSelections(limit) {
+
+ return 1;
+}
+
+combinatoricSelections(1000000);
+```
+
+# --solutions--
+
+```js
+function combinatoricSelections(limit) {
+ const factorial = n =>
+ Array.apply(null, { length: n })
+ .map((_, i) => i + 1)
+ .reduce((p, c) => p * c, 1);
+
+ let result = 0;
+ const nMax = 100;
+
+ for (let n = 1; n <= nMax; n++) {
+ for (let r = 0; r <= n; r++) {
+ if (factorial(n) / (factorial(r) * factorial(n - r)) >= limit)
+ result++;
+ }
+ }
+
+ return result;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-54-poker-hands.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-54-poker-hands.md
new file mode 100644
index 00000000000..b08e9a13bda
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-54-poker-hands.md
@@ -0,0 +1,1096 @@
+---
+id: 5900f3a21000cf542c50feb5
+title: 'Problem 54: Poker hands'
+challengeType: 1
+forumTopicId: 302165
+dashedName: problem-54-poker-hands
+---
+
+# --description--
+
+In the card game poker, a hand consists of five cards and are ranked, from lowest to highest, in the following way:
+
+-
+
- High Card: Highest value card. +
- One Pair: Two cards of the same value. +
- Two Pairs: Two different pairs. +
- Three of a Kind: Three cards of the same value. +
- Straight: All cards are consecutive values. +
- Flush: All cards of the same suit. +
- Full House: Three of a kind and a pair. +
- Four of a Kind: Four cards of the same value. +
- Straight Flush: All cards are consecutive values of same suit. +
- Royal Flush: Ten, Jack, Queen, King, Ace, in same suit. +
Pair of Fives | 2C 3S 8S 8D TD
Pair of Eights | Player 2 | +| 2 | 5D 8C 9S JS AC
Highest card Ace | 2C 5C 7D 8S QH
Highest card Queen | Player 1 | +| 3 | 2D 9C AS AH AC
Three Aces | 3D 6D 7D TD QD
Flush with Diamonds | Player 2 | +| 4 | 4D 6S 9H QH QC
Pair of Queens
Highest card Nine | 3D 6D 7H QD QS
Pair of Queens
Highest card Seven | Player 1 | +| 5 | 2H 2D 4C 4D 4S
Full House
with Three Fours | 3C 3D 3S 9S 9D
Full House
with Three Threes | Player 1 | + +The global array (`handsArr`) passed to the function, contains one-thousand random hands dealt to two players. Each line of the file contains ten cards (separated by a single space): the first five are Player 1's cards and the last five are Player 2's cards. You can assume that all hands are valid (no invalid characters or repeated cards), each player's hand is in no specific order, and in each hand there is a clear winner. + +How many hands does Player 1 win? + +# --hints-- + +`pokerHands(testArr)` should return a number. + +```js +assert(typeof pokerHands(testArr) === 'number'); +``` + +`pokerHands(testArr)` should return 2. + +```js +assert.strictEqual(pokerHands(testArr), 2); +``` + +`pokerHands(handsArr)` should return 376. + +```js +assert.strictEqual(pokerHands(handsArr), 376); +``` + +# --seed-- + +## --before-user-code-- + +```js +const handsArr = [ + '8C TS KC 9H 4S 7D 2S 5D 3S AC', + '5C AD 5D AC 9C 7C 5H 8D TD KS', + '3H 7H 6S KC JS QH TD JC 2D 8S', + 'TH 8H 5C QS TC 9H 4D JC KS JS', + '7C 5H KC QH JD AS KH 4C AD 4S', + '5H KS 9C 7D 9H 8D 3S 5D 5C AH', + '6H 4H 5C 3H 2H 3S QH 5S 6S AS', + 'TD 8C 4H 7C TC KC 4C 3H 7S KS', + '7C 9C 6D KD 3H 4C QS QC AC KH', + 'JC 6S 5H 2H 2D KD 9D 7C AS JS', + 'AD QH TH 9D 8H TS 6D 3S AS AC', + '2H 4S 5C 5S TC KC JD 6C TS 3C', + 'QD AS 6H JS 2C 3D 9H KC 4H 8S', + 'KD 8S 9S 7C 2S 3S 6D 6S 4H KC', + '3C 8C 2D 7D 4D 9S 4S QH 4H JD', + '8C KC 7S TC 2D TS 8H QD AC 5C', + '3D KH QD 6C 6S AD AS 8H 2H QS', + '6S 8D 4C 8S 6C QH TC 6D 7D 9D', + '2S 8D 8C 4C TS 9S 9D 9C AC 3D', + '3C QS 2S 4H JH 3D 2D TD 8S 9H', + '5H QS 8S 6D 3C 8C JD AS 7H 7D', + '6H TD 9D AS JH 6C QC 9S KD JC', + 'AH 8S QS 4D TH AC TS 3C 3D 5C', + '5S 4D JS 3D 8H 6C TS 3S AD 8C', + '6D 7C 5D 5H 3S 5C JC 2H 5S 3D', + '5H 6H 2S KS 3D 5D JD 7H JS 8H', + 'KH 4H AS JS QS QC TC 6D 7C KS', + '3D QS TS 2H JS 4D AS 9S JC KD', + 'QD 5H 4D 5D KH 7H 3D JS KD 4H', + '2C 9H 6H 5C 9D 6C JC 2D TH 9S', + '7D 6D AS QD JH 4D JS 7C QS 5C', + '3H KH QD AD 8C 8H 3S TH 9D 5S', + 'AH 9S 4D 9D 8S 4H JS 3C TC 8D', + '2C KS 5H QD 3S TS 9H AH AD 8S', + '5C 7H 5D KD 9H 4D 3D 2D KS AD', + 'KS KC 9S 6D 2C QH 9D 9H TS TC', + '9C 6H 5D QH 4D AD 6D QC JS KH', + '9S 3H 9D JD 5C 4D 9H AS TC QH', + '2C 6D JC 9C 3C AD 9S KH 9D 7D', + 'KC 9C 7C JC JS KD 3H AS 3C 7D', + 'QD KH QS 2C 3S 8S 8H 9H 9C JC', + 'QH 8D 3C KC 4C 4H 6D AD 9H 9D', + '3S KS QS 7H KH 7D 5H 5D JD AD', + '2H 2C 6H TH TC 7D 8D 4H 8C AS', + '4S 2H AC QC 3S 6D TH 4D 4C KH', + '4D TC KS AS 7C 3C 6D 2D 9H 6C', + '8C TD 5D QS 2C 7H 4C 9C 3H 9H', + '5H JH TS 7S TD 6H AD QD 8H 8S', + '5S AD 9C 8C 7C 8D 5H 9D 8S 2S', + '4H KH KS 9S 2S KC 5S AD 4S 7D', + 'QS 9C QD 6H JS 5D AC 8D 2S AS', + 'KH AC JC 3S 9D 9S 3C 9C 5S JS', + 'AD 3C 3D KS 3S 5C 9C 8C TS 4S', + 'JH 8D 5D 6H KD QS QD 3D 6C KC', + '8S JD 6C 3S 8C TC QC 3C QH JS', + 'KC JC 8H 2S 9H 9C JH 8S 8C 9S', + '8S 2H QH 4D QC 9D KC AS TH 3C', + '8S 6H TH 7C 2H 6S 3C 3H AS 7S', + 'QH 5S JS 4H 5H TS 8H AH AC JC', + '9D 8H 2S 4S TC JC 3C 7H 3H 5C', + '3D AD 3C 3S 4C QC AS 5D TH 8C', + '6S 9D 4C JS KH AH TS JD 8H AD', + '4C 6S 9D 7S AC 4D 3D 3S TC JD', + 'AD 7H 6H 4H JH KC TD TS 7D 6S', + '8H JH TC 3S 8D 8C 9S 2C 5C 4D', + '2C 9D KC QH TH QS JC 9C 4H TS', + 'QS 3C QD 8H KH 4H 8D TD 8S AC', + '7C 3C TH 5S 8H 8C 9C JD TC KD', + 'QC TC JD TS 8C 3H 6H KD 7C TD', + 'JH QS KS 9C 6D 6S AS 9H KH 6H', + '2H 4D AH 2D JH 6H TD 5D 4H JD', + 'KD 8C 9S JH QD JS 2C QS 5C 7C', + '4S TC 7H 8D 2S 6H 7S 9C 7C KC', + '8C 5D 7H 4S TD QC 8S JS 4H KS', + 'AD 8S JH 6D TD KD 7C 6C 2D 7D', + 'JC 6H 6S JS 4H QH 9H AH 4C 3C', + '6H 5H AS 7C 7S 3D KH KC 5D 5C', + 'JC 3D TD AS 4D 6D 6S QH JD KS', + '8C 7S 8S QH 2S JD 5C 7H AH QD', + '8S 3C 6H 6C 2C 8D TD 7D 4C 4D', + '5D QH KH 7C 2S 7H JS 6D QC QD', + 'AD 6C 6S 7D TH 6H 2H 8H KH 4H', + 'KS JS KD 5D 2D KH 7D 9C 8C 3D', + '9C 6D QD 3C KS 3S 7S AH JD 2D', + 'AH QH AS JC 8S 8H 4C KC TH 7D', + 'JC 5H TD 7C 5D KD 4C AD 8H JS', + 'KC 2H AC AH 7D JH KH 5D 7S 6D', + '9S 5S 9C 6H 8S TD JD 9H 6C AC', + '7D 8S 6D TS KD 7H AC 5S 7C 5D', + 'AH QC JC 4C TC 8C 2H TS 2C 7D', + 'KD KC 6S 3D 7D 2S 8S 3H 5S 5C', + '8S 5D 8H 4C 6H KC 3H 7C 5S KD', + 'JH 8C 3D 3C 6C KC TD 7H 7C 4C', + 'JC KC 6H TS QS TD KS 8H 8C 9S', + '6C 5S 9C QH 7D AH KS KC 9S 2C', + '4D 4S 8H TD 9C 3S 7D 9D AS TH', + '6S 7D 3C 6H 5D KD 2C 5C 9D 9C', + '2H KC 3D AD 3H QD QS 8D JC 4S', + '8C 3H 9C 7C AD 5D JC 9D JS AS', + '5D 9H 5C 7H 6S 6C QC JC QD 9S', + 'JC QS JH 2C 6S 9C QC 3D 4S TC', + '4H 5S 8D 3D 4D 2S KC 2H JS 2C', + 'TD 3S TH KD 4D 7H JH JS KS AC', + '7S 8C 9S 2D 8S 7D 5C AD 9D AS', + '8C 7H 2S 6C TH 3H 4C 3S 8H AC', + 'KD 5H JC 8H JD 2D 4H TD JH 5C', + '3D AS QH KS 7H JD 8S 5S 6D 5H', + '9S 6S TC QS JC 5C 5D 9C TH 8C', + '5H 3S JH 9H 2S 2C 6S 7S AS KS', + '8C QD JC QS TC QC 4H AC KH 6C', + 'TC 5H 7D JH 4H 2H 8D JC KS 4D', + '5S 9C KH KD 9H 5C TS 3D 7D 2D', + '5H AS TC 4D 8C 2C TS 9D 3H 8D', + '6H 8D 2D 9H JD 6C 4S 5H 5S 6D', + 'AD 9C JC 7D 6H 9S 6D JS 9H 3C', + 'AD JH TC QS 4C 5D 9S 7C 9C AH', + 'KD 6H 2H TH 8S QD KS 9D 9H AS', + '4H 8H 8D 5H 6C AH 5S AS AD 8S', + 'QS 5D 4S 2H TD KS 5H AC 3H JC', + '9C 7D QD KD AC 6D 5H QH 6H 5S', + 'KC AH QH 2H 7D QS 3H KS 7S JD', + '6C 8S 3H 6D KS QD 5D 5C 8H TC', + '9H 4D 4S 6S 9D KH QC 4H 6C JD', + 'TD 2D QH 4S 6H JH KD 3C QD 8C', + '4S 6H 7C QD 9D AS AH 6S AD 3C', + '2C KC TH 6H 8D AH 5C 6D 8S 5D', + 'TD TS 7C AD JC QD 9H 3C KC 7H', + '5D 4D 5S 8H 4H 7D 3H JD KD 2D', + 'JH TD 6H QS 4S KD 5C 8S 7D 8H', + 'AC 3D AS 8C TD 7H KH 5D 6C JD', + '9D KS 7C 6D QH TC JD KD AS KC', + 'JH 8S 5S 7S 7D AS 2D 3D AD 2H', + '2H 5D AS 3C QD KC 6H 9H 9S 2C', + '9D 5D TH 4C JH 3H 8D TC 8H 9H', + '6H KD 2C TD 2H 6C 9D 2D JS 8C', + 'KD 7S 3C 7C AS QH TS AD 8C 2S', + 'QS 8H 6C JS 4C 9S QC AD TD TS', + '2H 7C TS TC 8C 3C 9H 2D 6D JC', + 'TC 2H 8D JH KS 6D 3H TD TH 8H', + '9D TD 9H QC 5D 6C 8H 8C KC TS', + '2H 8C 3D AH 4D TH TC 7D 8H KC', + 'TS 5C 2D 8C 6S KH AH 5H 6H KC', + '5S 5D AH TC 4C JD 8D 6H 8C 6C', + 'KC QD 3D 8H 2D JC 9H 4H AD 2S', + 'TD 6S 7D JS KD 4H QS 2S 3S 8C', + '4C 9H JH TS 3S 4H QC 5S 9S 9C', + '2C KD 9H JS 9S 3H JC TS 5D AC', + 'AS 2H 5D AD 5H JC 7S TD JS 4C', + '2D 4S 8H 3D 7D 2C AD KD 9C TS', + '7H QD JH 5H JS AC 3D TH 4C 8H', + '6D KH KC QD 5C AD 7C 2D 4H AC', + '3D 9D TC 8S QD 2C JC 4H JD AH', + '6C TD 5S TC 8S AH 2C 5D AS AC', + 'TH 7S 3D AS 6C 4C 7H 7D 4H AH', + '5C 2H KS 6H 7S 4H 5H 3D 3C 7H', + '3C 9S AC 7S QH 2H 3D 6S 3S 3H', + '2D 3H AS 2C 6H TC JS 6S 9C 6C', + 'QH KD QD 6D AC 6H KH 2C TS 8C', + '8H 7D 3S 9H 5D 3H 4S QC 9S 5H', + '2D 9D 7H 6H 3C 8S 5H 4D 3S 4S', + 'KD 9S 4S TC 7S QC 3S 8S 2H 7H', + 'TC 3D 8C 3H 6C 2H 6H KS KD 4D', + 'KC 3D 9S 3H JS 4S 8H 2D 6C 8S', + '6H QS 6C TC QD 9H 7D 7C 5H 4D', + 'TD 9D 8D 6S 6C TC 5D TS JS 8H', + '4H KC JD 9H TC 2C 6S 5H 8H AS', + 'JS 9C 5C 6S 9D JD 8H KC 4C 6D', + '4D 8D 8S 6C 7C 6H 7H 8H 5C KC', + 'TC 3D JC 6D KS 9S 6H 7S 9C 2C', + '6C 3S KD 5H TS 7D 9H 9S 6H KH', + '3D QD 4C 6H TS AC 3S 5C 2H KD', + '4C AS JS 9S 7C TS 7H 9H JC KS', + '4H 8C JD 3H 6H AD 9S 4S 5S KS', + '4C 2C 7D 3D AS 9C 2S QS KC 6C', + '8S 5H 3D 2S AC 9D 6S 3S 4D TD', + 'QD TH 7S TS 3D AC 7H 6C 5D QC', + 'TC QD AD 9C QS 5C 8D KD 3D 3C', + '9D 8H AS 3S 7C 8S JD 2D 8D KC', + '4C TH AC QH JS 8D 7D 7S 9C KH', + '9D 8D 4C JH 2C 2S QD KD TS 4H', + '4D 6D 5D 2D JH 3S 8S 3H TC KH', + 'AD 4D 2C QS 8C KD JH JD AH 5C', + '5C 6C 5H 2H JH 4H KS 7C TC 3H', + '3C 4C QC 5D JH 9C QD KH 8D TC', + '3H 9C JS 7H QH AS 7C 9H 5H JC', + '2D 5S QD 4S 3C KC 6S 6C 5C 4C', + '5D KH 2D TS 8S 9C AS 9S 7C 4C', + '7C AH 8C 8D 5S KD QH QS JH 2C', + '8C 9D AH 2H AC QC 5S 8H 7H 2C', + 'QD 9H 5S QS QC 9C 5H JC TH 4H', + '6C 6S 3H 5H 3S 6H KS 8D AC 7S', + 'AC QH 7H 8C 4S KC 6C 3D 3S TC', + '9D 3D JS TH AC 5H 3H 8S 3S TC', + 'QD KH JS KS 9S QC 8D AH 3C AC', + '5H 6C KH 3S 9S JH 2D QD AS 8C', + '6C 4D 7S 7H 5S JC 6S 9H 4H JH', + 'AH 5S 6H 9S AD 3S TH 2H 9D 8C', + '4C 8D 9H 7C QC AD 4S 9C KC 5S', + '9D 6H 4D TC 4C JH 2S 5D 3S AS', + '2H 6C 7C KH 5C AD QS TH JD 8S', + '3S 4S 7S AH AS KC JS 2S AD TH', + 'JS KC 2S 7D 8C 5C 9C TS 5H 9D', + '7S 9S 4D TD JH JS KH 6H 5D 2C', + 'JD JS JC TH 2D 3D QD 8C AC 5H', + '7S KH 5S 9D 5D TD 4S 6H 3C 2D', + '4S 5D AC 8D 4D 7C AD AS AH 9C', + '6S TH TS KS 2C QC AH AS 3C 4S', + '2H 8C 3S JC 5C 7C 3H 3C KH JH', + '7S 3H JC 5S 6H 4C 2S 4D KC 7H', + '4D 7C 4H 9S 8S 6S AD TC 6C JC', + 'KH QS 3S TC 4C 8H 8S AC 3C TS', + 'QD QS TH 3C TS 7H 7D AH TD JC', + 'TD JD QC 4D 9S 7S TS AD 7D AC', + 'AH 7H 4S 6D 7C 2H 9D KS JC TD', + '7C AH JD 4H 6D QS TS 2H 2C 5C', + 'TC KC 8C 9S 4C JS 3C JC 6S AH', + 'AS 7D QC 3D 5S JC JD 9D TD KH', + 'TH 3C 2S 6H AH AC 5H 5C 7S 8H', + 'QC 2D AC QD 2S 3S JD QS 6S 8H', + 'KC 4H 3C 9D JS 6H 3S 8S AS 8C', + '7H KC 7D JD 2H JC QH 5S 3H QS', + '9H TD 3S 8H 7S AC 5C 6C AH 7C', + '8D 9H AH JD TD QS 7D 3S 9C 8S', + 'AH QH 3C JD KC 4S 5S 5D TD KS', + '9H 7H 6S JH TH 4C 7C AD 5C 2D', + '7C KD 5S TC 9D 6S 6C 5D 2S TH', + 'KC 9H 8D 5H 7H 4H QC 3D 7C AS', + '6S 8S QC TD 4S 5C TH QS QD 2S', + '8S 5H TH QC 9H 6S KC 7D 7C 5C', + '7H KD AH 4D KH 5C 4S 2D KC QH', + '6S 2C TD JC AS 4D 6C 8C 4H 5S', + 'JC TC JD 5S 6S 8D AS 9D AD 3S', + '6D 6H 5D 5S TC 3D 7D QS 9D QD', + '4S 6C 8S 3S 7S AD KS 2D 7D 7C', + 'KC QH JC AC QD 5D 8D QS 7H 7D', + 'JS AH 8S 5H 3D TD 3H 4S 6C JH', + '4S QS 7D AS 9H JS KS 6D TC 5C', + '2D 5C 6H TC 4D QH 3D 9H 8S 6C', + '6D 7H TC TH 5S JD 5C 9C KS KD', + '8D TD QH 6S 4S 6C 8S KC 5C TC', + '5S 3D KS AC 4S 7D QD 4C TH 2S', + 'TS 8H 9S 6S 7S QH 3C AH 7H 8C', + '4C 8C TS JS QC 3D 7D 5D 7S JH', + '8S 7S 9D QC AC 7C 6D 2H JH KC', + 'JS KD 3C 6S 4S 7C AH QC KS 5H', + 'KS 6S 4H JD QS TC 8H KC 6H AS', + 'KH 7C TC 6S TD JC 5C 7D AH 3S', + '3H 4C 4H TC TH 6S 7H 6D 9C QH', + '7D 5H 4S 8C JS 4D 3D 8S QH KC', + '3H 6S AD 7H 3S QC 8S 4S 7S JS', + '3S JD KH TH 6H QS 9C 6C 2D QD', + '4S QH 4D 5H KC 7D 6D 8D TH 5S', + 'TD AD 6S 7H KD KH 9H 5S KC JC', + '3H QC AS TS 4S QD KS 9C 7S KC', + 'TS 6S QC 6C TH TC 9D 5C 5D KD', + 'JS 3S 4H KD 4C QD 6D 9S JC 9D', + '8S JS 6D 4H JH 6H 6S 6C KS KH', + 'AC 7D 5D TC 9S KH 6S QD 6H AS', + 'AS 7H 6D QH 8D TH 2S KH 5C 5H', + '4C 7C 3D QC TC 4S KH 8C 2D JS', + '6H 5D 7S 5H 9C 9H JH 8S TH 7H', + 'AS JS 2S QD KH 8H 4S AC 8D 8S', + '3H 4C TD KD 8C JC 5C QS 2D JD', + 'TS 7D 5D 6C 2C QS 2H 3C AH KS', + '4S 7C 9C 7D JH 6C 5C 8H 9D QD', + '2S TD 7S 6D 9C 9S QS KH QH 5C', + 'JC 6S 9C QH JH 8D 7S JS KH 2H', + '8D 5H TH KC 4D 4S 3S 6S 3D QS', + '2D JD 4C TD 7C 6D TH 7S JC AH', + 'QS 7S 4C TH 9D TS AD 4D 3H 6H', + '2D 3H 7D JD 3D AS 2S 9C QC 8S', + '4H 9H 9C 2C 7S JH KD 5C 5D 6H', + 'TC 9H 8H JC 3C 9S 8D KS AD KC', + 'TS 5H JD QS QH QC 8D 5D KH AH', + '5D AS 8S 6S 4C AH QC QD TH 7H', + '3H 4H 7D 6S 4S 9H AS 8H JS 9D', + 'JD 8C 2C 9D 7D 5H 5S 9S JC KD', + 'KD 9C 4S QD AH 7C AD 9D AC TD', + '6S 4H 4S 9C 8D KS TC 9D JH 7C', + '5S JC 5H 4S QH AC 2C JS 2S 9S', + '8C 5H AS QD AD 5C 7D 8S QC TD', + 'JC 4C 8D 5C KH QS 4D 6H 2H 2C', + 'TH 4S 2D KC 3H QD AC 7H AD 9D', + 'KH QD AS 8H TH KC 8D 7S QH 8C', + 'JC 6C 7D 8C KH AD QS 2H 6S 2D', + 'JC KH 2D 7D JS QC 5H 4C 5D AD', + 'TS 3S AD 4S TD 2D TH 6S 9H JH', + '9H 2D QS 2C 4S 3D KH AS AC 9D', + 'KH 6S 8H 4S KD 7D 9D TS QD QC', + 'JH 5H AH KS AS AD JC QC 5S KH', + '5D 7D 6D KS KD 3D 7C 4D JD 3S', + 'AC JS 8D 5H 9C 3H 4H 4D TS 2C', + '6H KS KH 9D 7C 2S 6S 8S 2H 3D', + '6H AC JS 7S 3S TD 8H 3H 4H TH', + '9H TC QC KC 5C KS 6H 4H AC 8S', + 'TC 7D QH 4S JC TS 6D 6C AC KH', + 'QH 7D 7C JH QS QD TH 3H 5D KS', + '3D 5S 8D JS 4C 2C KS 7H 9C 4H', + '5H 8S 4H TD 2C 3S QD QC 3H KC', + 'QC JS KD 9C AD 5S 9D 7D 7H TS', + '8C JC KH 7C 7S 6C TS 2C QD TH', + '5S 9D TH 3C 7S QH 8S 9C 2H 5H', + '5D 9H 6H 2S JS KH 3H 7C 2H 5S', + 'JD 5D 5S 2C TC 2S 6S 6C 3C 8S', + '4D KH 8H 4H 2D KS 3H 5C 2S 9H', + '3S 2D TD 7H 8S 6H JD KC 9C 8D', + '6S QD JH 7C 9H 5H 8S 8H TH TD', + 'QS 7S TD 7D TS JC KD 7C 3C 2C', + '3C JD 8S 4H 2D 2S TD AS 4D AC', + 'AH KS 6C 4C 4S 7D 8C 9H 6H AS', + '5S 3C 9S 2C QS KD 4D 4S AC 5D', + '2D TS 2C JS KH QH 5D 8C AS KC', + 'KD 3H 6C TH 8S 7S KH 6H 9S AC', + '6H 7S 6C QS AH 2S 2H 4H 5D 5H', + '5H JC QD 2C 2S JD AS QC 6S 7D', + '6C TC AS KD 8H 9D 2C 7D JH 9S', + '2H 4C 6C AH 8S TD 3H TH 7C TS', + 'KD 4S TS 6C QH 8D 9D 9C AH 7D', + '6D JS 5C QD QC 9C 5D 8C 2H KD', + '3C QH JH AD 6S AH KC 8S 6D 6H', + '3D 7C 4C 7S 5S 3S 6S 5H JC 3C', + 'QH 7C 5H 3C 3S 8C TS 4C KD 9C', + 'QD 3S 7S 5H 7H QH JC 7C 8C KD', + '3C KD KH 2S 4C TS AC 6S 2C 7C', + '2C KH 3C 4C 6H 4D 5H 5S 7S QD', + '4D 7C 8S QD TS 9D KS 6H KD 3C', + 'QS 4D TS 7S 4C 3H QD 8D 9S TC', + 'TS QH AC 6S 3C 9H 9D QS 8S 6H', + '3S 7S 5D 4S JS 2D 6C QH 6S TH', + '4C 4H AS JS 5D 3D TS 9C AC 8S', + '6S 9C 7C 3S 5C QS AD AS 6H 3C', + '9S 8C 7H 3H 6S 7C AS 9H JD KH', + '3D 3H 7S 4D 6C 7C AC 2H 9C TH', + '4H 5S 3H AC TC TH 9C 9H 9S 8D', + '8D 9H 5H 4D 6C 2H QD 6S 5D 3S', + '4C 5C JD QS 4D 3H TH AC QH 8C', + 'QC 5S 3C 7H AD 4C KS 4H JD 6D', + 'QS AH 3H KS 9H 2S JS JH 5H 2H', + '2H 5S TH 6S TS 3S KS 3C 5H JS', + '2D 9S 7H 3D KC JH 6D 7D JS TD', + 'AC JS 8H 2C 8C JH JC 2D TH 7S', + '5D 9S 8H 2H 3D TC AH JC KD 9C', + '9D QD JC 2H 6D KH TS 9S QH TH', + '2C 8D 4S JD 5H 3H TH TC 9C KC', + 'AS 3D 9H 7D 4D TH KH 2H 7S 3H', + '4H 7S KS 2S JS TS 8S 2H QD 8D', + '5S 6H JH KS 8H 2S QC AC 6S 3S', + 'JC AS AD QS 8H 6C KH 4C 4D QD', + '2S 3D TS TD 9S KS 6S QS 5C 8D', + '3C 6D 4S QC KC JH QD TH KH AD', + '9H AH 4D KS 2S 8D JH JC 7C QS', + '2D 6C TH 3C 8H QD QH 2S 3S KS', + '6H 5D 9S 4C TS TD JS QD 9D JD', + '5H 8H KH 8S KS 7C TD AD 4S KD', + '2C 7C JC 5S AS 6C 7D 8S 5H 9C', + '6S QD 9S TS KH QS 5S QH 3C KC', + '7D 3H 3C KD 5C AS JH 7H 6H JD', + '9D 5C 9H KC 8H KS 4S AD 4D 2S', + '3S JD QD 8D 2S 7C 5S 6S 5H TS', + '6D 9S KC TD 3S 6H QD JD 5C 8D', + '5H 9D TS KD 8D 6H TD QC 4C 7D', + '6D 4S JD 9D AH 9S AS TD 9H QD', + '2D 5S 2H 9C 6H 9S TD QC 7D TC', + '3S 2H KS TS 2C 9C 8S JS 9D 7D', + '3C KC 6D 5D 6C 6H 8S AS 7S QS', + 'JH 9S 2H 8D 4C 8H 9H AD TH KH', + 'QC AS 2S JS 5C 6H KD 3H 7H 2C', + 'QD 8H 2S 8D 3S 6D AH 2C TC 5C', + 'JD JS TS 8S 3H 5D TD KC JC 6H', + '6S QS TC 3H 5D AH JC 7C 7D 4H', + '7C 5D 8H 9C 2H 9H JH KH 5S 2C', + '9C 7H 6S TH 3S QC QD 4C AC JD', + '2H 5D 9S 7D KC 3S QS 2D AS KH', + '2S 4S 2H 7D 5C TD TH QH 9S 4D', + '6D 3S TS 6H 4H KS 9D 8H 5S 2D', + '9H KS 4H 3S 5C 5D KH 6H 6S JS', + 'KC AS 8C 4C JC KH QC TH QD AH', + '6S KH 9S 2C 5H TC 3C 7H JC 4D', + 'JD 4S 6S 5S 8D 7H 7S 4D 4C 2H', + '7H 9H 5D KH 9C 7C TS TC 7S 5H', + '4C 8D QC TS 4S 9H 3D AD JS 7C', + '8C QS 5C 5D 3H JS AH KC 4S 9D', + 'TS JD 8S QS TH JH KH 2D QD JS', + 'JD QC 5D 6S 9H 3S 2C 8H 9S TS', + '2S 4C AD 7H JC 5C 2D 6D 4H 3D', + '7S JS 2C 4H 8C AD QD 9C 3S TD', + 'JD TS 4C 6H 9H 7D QD 6D 3C AS', + 'AS 7C 4C 6S 5D 5S 5C JS QC 4S', + 'KD 6S 9S 7C 3C 5S 7D JH QD JS', + '4S 7S JH 2C 8S 5D 7H 3D QH AD', + 'TD 6H 2H 8D 4H 2D 7C AD KH 5D', + 'TS 3S 5H 2C QD AH 2S 5C KH TD', + 'KC 4D 8C 5D AS 6C 2H 2S 9H 7C', + 'KD JS QC TS QS KH JH 2C 5D AD', + '3S 5H KC 6C 9H 3H 2H AD 7D 7S', + '7S JS JH KD 8S 7D 2S 9H 7C 2H', + '9H 2D 8D QC 6S AD AS 8H 5H 6C', + '2S 7H 6C 6D 7D 8C 5D 9D JC 3C', + '7C 9C 7H JD 2H KD 3S KH AD 4S', + 'QH AS 9H 4D JD KS KD TS KH 5H', + '4C 8H 5S 3S 3D 7D TD AD 7S KC', + 'JS 8S 5S JC 8H TH 9C 4D 5D KC', + '7C 5S 9C QD 2C QH JS 5H 8D KH', + 'TD 2S KS 3D AD KC 7S TC 3C 5D', + '4C 2S AD QS 6C 9S QD TH QH 5C', + '8C AD QS 2D 2S KC JD KS 6C JC', + '8D 4D JS 2H 5D QD 7S 7D QH TS', + '6S 7H 3S 8C 8S 9D QS 8H 6C 9S', + '4S TC 2S 5C QD 4D QS 6D TH 6S', + '3S 5C 9D 6H 8D 4C 7D TC 7C TD', + 'AH 6S AS 7H 5S KD 3H 5H AC 4C', + '8D 8S AH KS QS 2C AD 6H 7D 5D', + '6H 9H 9S 2H QS 8S 9C 5D 2D KD', + 'TS QC 5S JH 7D 7S TH 9S 9H AC', + '7H 3H 6S KC 4D 6D 5C 4S QD TS', + 'TD 2S 7C QD 3H JH 9D 4H 7S 7H', + 'KS 3D 4H 5H TC 2S AS 2D 6D 7D', + '8H 3C 7H TD 3H AD KC TH 9C KH', + 'TC 4C 2C 9S 9D 9C 5C 2H JD 3C', + '3H AC TS 5D AD 8D 6H QC 6S 8C', + '2S TS 3S JD 7H 8S QH 4C 5S 8D', + 'AC 4S 6C 3C KH 3D 7C 2D 8S 2H', + '4H 6C 8S TH 2H 4S 8H 9S 3H 7S', + '7C 4C 9C 2C 5C AS 5D KD 4D QH', + '9H 4H TS AS 7D 8D 5D 9S 8C 2H', + 'QC KD AC AD 2H 7S AS 3S 2D 9S', + '2H QC 8H TC 6D QD QS 5D KH 3C', + 'TH JD QS 4C 2S 5S AD 7H 3S AS', + '7H JS 3D 6C 3S 6D AS 9S AC QS', + '9C TS AS 8C TC 8S 6H 9D 8D 6C', + '4D JD 9C KC 7C 6D KS 3S 8C AS', + '3H 6S TC 8D TS 3S KC 9S 7C AS', + '8C QC 4H 4S 8S 6C 3S TC AH AC', + '4D 7D 5C AS 2H 6S TS QC AD TC', + 'QD QC 8S 4S TH 3D AH TS JH 4H', + '5C 2D 9S 2C 3H 3C 9D QD QH 7D', + 'KC 9H 6C KD 7S 3C 4D AS TC 2D', + '3D JS 4D 9D KS 7D TH QC 3H 3C', + '8D 5S 2H 9D 3H 8C 4C 4H 3C TH', + 'JC TH 4S 6S JD 2D 4D 6C 3D 4C', + 'TS 3S 2D 4H AC 2C 6S 2H JH 6H', + 'TD 8S AD TC AH AC JH 9S 6S 7S', + '6C KC 4S JD 8D 9H 5S 7H QH AH', + 'KD 8D TS JH 5C 5H 3H AD AS JS', + '2D 4H 3D 6C 8C 7S AD 5D 5C 8S', + 'TD 5D 7S 9C 4S 5H 6C 8C 4C 8S', + 'JS QH 9C AS 5C QS JC 3D QC 7C', + 'JC 9C KH JH QS QC 2C TS 3D AD', + '5D JH AC 5C 9S TS 4C JD 8C KS', + 'KC AS 2D KH 9H 2C 5S 4D 3D 6H', + 'TH AH 2D 8S JC 3D 8C QH 7S 3S', + '8H QD 4H JC AS KH KS 3C 9S 6D', + '9S QH 7D 9C 4S AC 7H KH 4D KD', + 'AH AD TH 6D 9C 9S KD KS QH 4H', + 'QD 6H 9C 7C QS 6D 6S 9D 5S JH', + 'AH 8D 5H QD 2H JC KS 4H KH 5S', + '5C 2S JS 8D 9C 8C 3D AS KC AH', + 'JD 9S 2H QS 8H 5S 8C TH 5C 4C', + 'QC QS 8C 2S 2C 3S 9C 4C KS KH', + '2D 5D 8S AH AD TD 2C JS KS 8C', + 'TC 5S 5H 8H QC 9H 6H JD 4H 9S', + '3C JH 4H 9H AH 4S 2H 4C 8D AC', + '8S TH 4D 7D 6D QD QS 7S TC 7C', + 'KH 6D 2D JD 5H JS QD JH 4H 4S', + '9C 7S JH 4S 3S TS QC 8C TC 4H', + 'QH 9D 4D JH QS 3S 2C 7C 6C 2D', + '4H 9S JD 5C 5H AH 9D TS 2D 4C', + 'KS JH TS 5D 2D AH JS 7H AS 8D', + 'JS AH 8C AD KS 5S 8H 2C 6C TH', + '2H 5D AD AC KS 3D 8H TS 6H QC', + '6D 4H TS 9C 5H JS JH 6S JD 4C', + 'JH QH 4H 2C 6D 3C 5D 4C QS KC', + '6H 4H 6C 7H 6S 2S 8S KH QC 8C', + '3H 3D 5D KS 4H TD AD 3S 4D TS', + '5S 7C 8S 7D 2C KS 7S 6C 8C JS', + '5D 2H 3S 7C 5C QD 5H 6D 9C 9H', + 'JS 2S KD 9S 8D TD TS AC 8C 9D', + '5H QD 2S AC 8C 9H KS 7C 4S 3C', + 'KH AS 3H 8S 9C JS QS 4S AD 4D', + 'AS 2S TD AD 4D 9H JC 4C 5H QS', + '5D 7C 4H TC 2D 6C JS 4S KC 3S', + '4C 2C 5D AC 9H 3D JD 8S QS QH', + '2C 8S 6H 3C QH 6D TC KD AC AH', + 'QC 6C 3S QS 4S AC 8D 5C AD KH', + '5S 4C AC KH AS QC 2C 5C 8D 9C', + '8H JD 3C KH 8D 5C 9C QD QH 9D', + '7H TS 2C 8C 4S TD JC 9C 5H QH', + 'JS 4S 2C 7C TH 6C AS KS 7S JD', + 'JH 7C 9H 7H TC 5H 3D 6D 5D 4D', + '2C QD JH 2H 9D 5S 3D TD AD KS', + 'JD QH 3S 4D TH 7D 6S QS KS 4H', + 'TC KS 5S 8D 8H AD 2S 2D 4C JH', + '5S JH TC 3S 2D QS 9D 4C KD 9S', + 'AC KH 3H AS 9D KC 9H QD 6C 6S', + '9H 7S 3D 5C 7D KC TD 8H 4H 6S', + '3C 7H 8H TC QD 4D 7S 6S QH 6C', + '6D AD 4C QD 6C 5D 7D 9D KS TS', + 'JH 2H JD 9S 7S TS KH 8D 5D 8H', + '2D 9S 4C 7D 9D 5H QD 6D AC 6S', + '7S 6D JC QD JH 4C 6S QS 2H 7D', + '8C TD JH KD 2H 5C QS 2C JS 7S', + 'TC 5H 4H JH QD 3S 5S 5D 8S KH', + 'KS KH 7C 2C 5D JH 6S 9C 6D JC', + '5H AH JD 9C JS KC 2H 6H 4D 5S', + 'AS 3C TH QC 6H 9C 8S 8C TD 7C', + 'KC 2C QD 9C KH 4D 7S 3C TS 9H', + '9C QC 2S TS 8C TD 9S QD 3S 3C', + '4D 9D TH JH AH 6S 2S JD QH JS', + 'QD 9H 6C KD 7D 7H 5D 6S 8H AH', + '8H 3C 4S 2H 5H QS QH 7S 4H AC', + 'QS 3C 7S 9S 4H 3S AH KS 9D 7C', + 'AD 5S 6S 2H 2D 5H TC 4S 3C 8C', + 'QH TS 6S 4D JS KS JH AS 8S 6D', + '2C 8S 2S TD 5H AS TC TS 6C KC', + 'KC TS 8H 2H 3H 7C 4C 5S TH TD', + 'KD AD KH 7H 7S 5D 5H 5S 2D 9C', + 'AD 9S 3D 7S 8C QC 7C 9C KD KS', + '3C QC 9S 8C 4D 5C AS QD 6C 2C', + '2H KC 8S JD 7S AC 8D 5C 2S 4D', + '9D QH 3D 2S TC 3S KS 3C 9H TD', + 'KD 6S AC 2C 7H 5H 3S 6C 6H 8C', + 'QH TC 8S 6S KH TH 4H 5D TS 4D', + '8C JS 4H 6H 2C 2H 7D AC QD 3D', + 'QS KC 6S 2D 5S 4H TD 3H JH 4C', + '7S 5H 7H 8H KH 6H QS TH KD 7D', + '5H AD KD 7C KH 5S TD 6D 3C 6C', + '8C 9C 5H JD 7C KC KH 7H 2H 3S', + '7S 4H AD 4D 8S QS TH 3D 7H 5S', + '8D TC KS KD 9S 6D AD JD 5C 2S', + '7H 8H 6C QD 2H 6H 9D TC 9S 7C', + '8D 6D 4C 7C 6C 3C TH KH JS JH', + '5S 3S 8S JS 9H AS AD 8H 7S KD', + 'JH 7C 2C KC 5H AS AD 9C 9S JS', + 'AD AC 2C 6S QD 7C 3H TH KS KD', + '9D JD 4H 8H 4C KH 7S TS 8C KC', + '3S 5S 2H 7S 6H 7D KS 5C 6D AD', + '5S 8C 9H QS 7H 7S 2H 6C 7D TD', + 'QS 5S TD AC 9D KC 3D TC 2D 4D', + 'TD 2H 7D JD QD 4C 7H 5D KC 3D', + '4C 3H 8S KD QH 5S QC 9H TC 5H', + '9C QD TH 5H TS 5C 9H AH QH 2C', + '4D 6S 3C AC 6C 3D 2C 2H TD TH', + 'AC 9C 5D QC 4D AD 8D 6D 8C KC', + 'AD 3C 4H AC 8D 8H 7S 9S TD JC', + '4H 9H QH JS 2D TH TD TC KD KS', + '5S 6S 9S 8D TH AS KH 5H 5C 8S', + 'JD 2S 9S 6S 5S 8S 5D 7S 7H 9D', + '5D 8C 4C 9D AD TS 2C 7D KD TC', + '8S QS 4D KC 5C 8D 4S KH JD KD', + 'AS 5C AD QH 7D 2H 9S 7H 7C TC', + '2S 8S JD KH 7S 6C 6D AD 5D QC', + '9H 6H 3S 8C 8H AH TC 4H JS TD', + '2C TS 4D 7H 2D QC 9C 5D TH 7C', + '6C 8H QC 5D TS JH 5C 5H 9H 4S', + '2D QC 7H AS JS 8S 2H 4C 4H 8D', + 'JS 6S AC KD 3D 3C 4S 7H TH KC', + 'QH KH 6S QS 5S 4H 3C QD 3S 3H', + '7H AS KH 8C 4H 9C 5S 3D 6S TS', + '9C 7C 3H 5S QD 2C 3D AD AC 5H', + 'JH TD 2D 4C TS 3H KH AD 3S 7S', + 'AS 4C 5H 4D 6S KD JC 3C 6H 2D', + '3H 6S 8C 2D TH 4S AH QH AD 5H', + '7C 2S 9H 7H KC 5C 6D 5S 3H JC', + '3C TC 9C 4H QD TD JH 6D 9H 5S', + '7C 6S 5C 5D 6C 4S 7H 9H 6H AH', + 'AD 2H 7D KC 2C 4C 2S 9S 7H 3S', + 'TH 4C 8S 6S 3S AD KS AS JH TD', + '5C TD 4S 4D AD 6S 5D TC 9C 7D', + '8H 3S 4D 4S 5S 6H 5C AC 3H 3D', + '9H 3C AC 4S QS 8S 9D QH 5H 4D', + 'JC 6C 5H TS AC 9C JD 8C 7C QD', + '8S 8H 9C JD 2D QC QH 6H 3C 8D', + 'KS JS 2H 6H 5H QH QS 3H 7C 6D', + 'TC 3H 4S 7H QC 2H 3S 8C JS KH', + 'AH 8H 5S 4C 9H JD 3H 7S JC AC', + '3C 2D 4C 5S 6C 4S QS 3S JD 3D', + '5H 2D TC AH KS 6D 7H AD 8C 6H', + '6C 7S 3C JD 7C 8H KS KH AH 6D', + 'AH 7D 3H 8H 8S 7H QS 5H 9D 2D', + 'JD AC 4H 7S 8S 9S KS AS 9D QH', + '7S 2C 8S 5S JH QS JC AH KD 4C', + 'AH 2S 9H 4H 8D TS TD 6H QH JD', + '4H JC 3H QS 6D 7S 9C 8S 9D 8D', + '5H TD 4S 9S 4C 8C 8D 7H 3H 3D', + 'QS KH 3S 2C 2S 3C 7S TD 4S QD', + '7C TD 4D 5S KH AC AS 7H 4C 6C', + '2S 5H 6D JD 9H QS 8S 2C 2H TD', + '2S TS 6H 9H 7S 4H JC 4C 5D 5S', + '2C 5H 7D 4H 3S QH JC JS 6D 8H', + '4C QH 7C QD 3S AD TH 8S 5S TS', + '9H TC 2S TD JC 7D 3S 3D TH QH', + '7D 4C 8S 5C JH 8H 6S 3S KC 3H', + 'JC 3H KH TC QH TH 6H 2C AC 5H', + 'QS 2H 9D 2C AS 6S 6C 2S 8C 8S', + '9H 7D QC TH 4H KD QS AC 7S 3C', + '4D JH 6S 5S 8H KS 9S QC 3S AS', + 'JD 2D 6S 7S TC 9H KC 3H 7D KD', + '2H KH 7C 4D 4S 3H JS QD 7D KC', + '4C JC AS 9D 3C JS 6C 8H QD 4D', + 'AH JS 3S 6C 4C 3D JH 6D 9C 9H', + '9H 2D 8C 7H 5S KS 6H 9C 2S TC', + '6C 8C AD 7H 6H 3D KH AS 5D TH', + 'KS 8C 3S TS 8S 4D 5S 9S 6C 4H', + '9H 4S 4H 5C 7D KC 2D 2H 9D JH', + '5C JS TC 9D 9H 5H 7S KH JC 6S', + '7C 9H 8H 4D JC KH JD 2H TD TC', + '8H 6C 2H 2C KH 6H 9D QS QH 5H', + 'AC 7D 2S 3D QD JC 2D 8D JD JH', + '2H JC 2D 7H 2C 3C 8D KD TD 4H', + '3S 4H 6D 8D TS 3H TD 3D 6H TH', + 'JH JC 3S AC QH 9H 7H 8S QC 2C', + '7H TD QS 4S 8S 9C 2S 5D 4D 2H', + '3D TS 3H 2S QC 8H 6H KC JC KS', + '5D JD 7D TC 8C 6C 9S 3D 8D AC', + '8H 6H JH 6C 5D 8D 8S 4H AD 2C', + '9D 4H 2D 2C 3S TS AS TC 3C 5D', + '4D TH 5H KS QS 6C 4S 2H 3D AD', + '5C KC 6H 2C 5S 3C 4D 2D 9H 9S', + 'JD 4C 3H TH QH 9H 5S AH 8S AC', + '7D 9S 6S 2H TD 9C 4H 8H QS 4C', + '3C 6H 5D 4H 8C 9C KC 6S QD QS', + '3S 9H KD TC 2D JS 8C 6S 4H 4S', + '2S 4C 8S QS 6H KH 3H TH 8C 5D', + '2C KH 5S 3S 7S 7H 6C 9D QD 8D', + '8H KS AC 2D KH TS 6C JS KC 7H', + '9C KS 5C TD QC AH 6C 5H 9S 7C', + '5D 4D 3H 4H 6S 7C 7S AH QD TD', + '2H 7D QC 6S TC TS AH 7S 9D 3H', + 'TH 5H QD 9S KS 7S 7C 6H 8C TD', + 'TH 2D 4D QC 5C 7D JD AH 9C 4H', + '4H 3H AH 8D 6H QC QH 9H 2H 2C', + '2D AD 4C TS 6H 7S TH 4H QS TD', + '3C KD 2H 3H QS JD TC QC 5D 8H', + 'KS JC QD TH 9S KD 8D 8C 2D 9C', + '3C QD KD 6D 4D 8D AH AD QC 8S', + '8H 3S 9D 2S 3H KS 6H 4C 7C KC', + 'TH 9S 5C 3D 7D 6H AC 7S 4D 2C', + '5C 3D JD 4D 2D 6D 5H 9H 4C KH', + 'AS 7H TD 6C 2H 3D QD KS 4C 4S', + 'JC 3C AC 7C JD JS 8H 9S QC 5D', + 'JD 6S 5S 2H AS 8C 7D 5H JH 3D', + '8D TC 5S 9S 8S 3H JC 5H 7S AS', + '5C TD 3D 7D 4H 8D 7H 4D 5D JS', + 'QS 9C KS TD 2S 8S 5C 2H 4H AS', + 'TH 7S 4H 7D 3H JD KD 5D 2S KC', + 'JD 7H 4S 8H 4C JS 6H QH 5S 4H', + '2C QS 8C 5S 3H QC 2S 6C QD AD', + '8C 3D JD TC 4H 2H AD 5S AC 2S', + '5D 2C JS 2D AD 9D 3D 4C 4S JH', + '8D 5H 5D 6H 7S 4D KS 9D TD JD', + '3D 6D 9C 2S AS 7D 5S 5C 8H JD', + '7C 8S 3S 6S 5H JD TC AD 7H 7S', + '2S 9D TS 4D AC 8D 6C QD JD 3H', + '9S KH 2C 3C AC 3D 5H 6H 8D 5D', + 'KS 3D 2D 6S AS 4C 2S 7C 7H KH', + 'AC 2H 3S JC 5C QH 4D 2D 5H 7S', + 'TS AS JD 8C 6H JC 8S 5S 2C 5D', + '7S QH 7H 6C QC 8H 2D 7C JD 2S', + '2C QD 2S 2H JC 9C 5D 2D JD JH', + '7C 5C 9C 8S 7D 6D 8D 6C 9S JH', + '2C AD 6S 5H 3S KS 7S 9D KH 4C', + '7H 6C 2C 5C TH 9D 8D 3S QC AH', + '5S KC 6H TC 5H 8S TH 6D 3C AH', + '9C KD 4H AD TD 9S 4S 7D 6H 5D', + '7H 5C 5H 6D AS 4C KD KH 4H 9D', + '3C 2S 5C 6C JD QS 2H 9D 7D 3H', + 'AC 2S 6S 7S JS QD 5C QS 6H AD', + '5H TH QC 7H TC 3S 7C 6D KC 3D', + '4H 3D QC 9S 8H 2C 3S JC KS 5C', + '4S 6S 2C 6H 8S 3S 3D 9H 3H JS', + '4S 8C 4D 2D 8H 9H 7D 9D AH TS', + '9S 2C 9H 4C 8D AS 7D 3D 6D 5S', + '6S 4C 7H 8C 3H 5H JC AH 9D 9C', + '2S 7C 5S JD 8C 3S 3D 4D 7D 6S', + '3C KC 4S 5D 7D 3D JD 7H 3H 4H', + '9C 9H 4H 4D TH 6D QD 8S 9S 7S', + '2H AC 8S 4S AD 8C 2C AH 7D TC', + 'TS 9H 3C AD KS TC 3D 8C 8H JD', + 'QC 8D 2C 3C 7D 7C JD 9H 9C 6C', + 'AH 6S JS JH 5D AS QC 2C JD TD', + '9H KD 2H 5D 2D 3S 7D TC AH TS', + 'TD 8H AS 5D AH QC AC 6S TC 5H', + 'KS 4S 7H 4D 8D 9C TC 2H 6H 3H', + '3H KD 4S QD QH 3D 8H 8C TD 7S', + '8S JD TC AH JS QS 2D KH KS 4D', + '3C AD JC KD JS KH 4S TH 9H 2C', + 'QC 5S JS 9S KS AS 7C QD 2S JD', + 'KC 5S QS 3S 2D AC 5D 9H 8H KS', + '6H 9C TC AD 2C 6D 5S JD 6C 7C', + 'QS KH TD QD 2C 3H 8S 2S QC AH', + '9D 9H JH TC QH 3C 2S JS 5C 7H', + '6C 3S 3D 2S 4S QD 2D TH 5D 2C', + '2D 6H 6D 2S JC QH AS 7H 4H KH', + '5H 6S KS AD TC TS 7C AC 4S 4H', + 'AD 3C 4H QS 8C 9D KS 2H 2D 4D', + '4S 9D 6C 6D 9C AC 8D 3H 7H KD', + 'JC AH 6C TS JD 6D AD 3S 5D QD', + 'JC JH JD 3S 7S 8S JS QC 3H 4S', + 'JD TH 5C 2C AD JS 7H 9S 2H 7S', + '8D 3S JH 4D QC AS JD 2C KC 6H', + '2C AC 5H KD 5S 7H QD JH AH 2D', + 'JC QH 8D 8S TC 5H 5C AH 8C 6C', + '3H JS 8S QD JH 3C 4H 6D 5C 3S', + '6D 4S 4C AH 5H 5S 3H JD 7C 8D', + '8H AH 2H 3H JS 3C 7D QC 4H KD', + '6S 2H KD 5H 8H 2D 3C 8S 7S QD', + '2S 7S KC QC AH TC QS 6D 4C 8D', + '5S 9H 2C 3S QD 7S 6C 2H 7C 9D', + '3C 6C 5C 5S JD JC KS 3S 5D TS', + '7C KS 6S 5S 2S 2D TC 2H 5H QS', + 'AS 7H 6S TS 5H 9S 9D 3C KD 2H', + '4S JS QS 3S 4H 7C 2S AC 6S 9D', + '8C JH 2H 5H 7C 5D QH QS KH QC', + '3S TD 3H 7C KC 8D 5H 8S KH 8C', + '4H KH JD TS 3C 7H AS QC JS 5S', + 'AH 9D 2C 8D 4D 2D 6H 6C KC 6S', + '2S 6H 9D 3S 7H 4D KH 8H KD 3D', + '9C TC AC JH KH 4D JD 5H TD 3S', + '7S 4H 9D AS 4C 7D QS 9S 2S KH', + '3S 8D 8S KS 8C JC 5C KH 2H 5D', + '8S QH 2C 4D KC JS QC 9D AC 6H', + '8S 8C 7C JS JD 6S 4C 9C AC 4S', + 'QH 5D 2C 7D JC 8S 2D JS JH 4C', + 'JS 4C 7S TS JH KC KH 5H QD 4S', + 'QD 8C 8D 2D 6S TD 9D AC QH 5S', + 'QH QC JS 3D 3C 5C 4H KH 8S 7H', + '7C 2C 5S JC 8S 3H QC 5D 2H KC', + '5S 8D KD 6H 4H QD QH 6D AH 3D', + '7S KS 6C 2S 4D AC QS 5H TS JD', + '7C 2D TC 5D QS AC JS QC 6C KC', + '2C KS 4D 3H TS 8S AD 4H 7S 9S', + 'QD 9H QH 5H 4H 4D KH 3S JC AD', + '4D AC KC 8D 6D 4C 2D KH 2C JD', + '2C 9H 2D AH 3H 6D 9C 7D TC KS', + '8C 3H KD 7C 5C 2S 4S 5H AS AH', + 'TH JD 4H KD 3H TC 5C 3S AC KH', + '6D 7H AH 7S QC 6H 2D TD JD AS', + 'JH 5D 7H TC 9S 7D JC AS 5S KH', + '2H 8C AD TH 6H QD KD 9H 6S 6C', + 'QH KC 9D 4D 3S JS JH 4H 2C 9H', + 'TC 7H KH 4H JC 7D 9S 3H QS 7S', + 'AD 7D JH 6C 7H 4H 3S 3H 4D QH', + 'JD 2H 5C AS 6C QC 4D 3C TC JH', + 'AC JD 3H 6H 4C JC AD 7D 7H 9H', + '4H TC TS 2C 8C 6S KS 2H JD 9S', + '4C 3H QS QC 9S 9H 6D KC 9D 9C', + '5C AD 8C 2C QH TH QD JC 8D 8H', + 'QC 2C 2S QD 9C 4D 3S 8D JH QS', + '9D 3S 2C 7S 7C JC TD 3C TC 9H', + '3C TS 8H 5C 4C 2C 6S 8D 7C 4H', + 'KS 7H 2H TC 4H 2C 3S AS AH QS', + '8C 2D 2H 2C 4S 4C 6S 7D 5S 3S', + 'TH QC 5D TD 3C QS KD KC KS AS', + '4D AH KD 9H KS 5C 4C 6H JC 7S', + 'KC 4H 5C QS TC 2H JC 9S AH QH', + '4S 9H 3H 5H 3C QD 2H QC JH 8H', + '5D AS 7H 2C 3D JH 6H 4C 6S 7D', + '9C JD 9H AH JS 8S QH 3H KS 8H', + '3S AC QC TS 4D AD 3D AH 8S 9H', + '7H 3H QS 9C 9S 5H JH JS AH AC', + '8D 3C JD 2H AC 9C 7H 5S 4D 8H', + '7C JH 9H 6C JS 9S 7H 8C 9D 4H', + '2D AS 9S 6H 4D JS JH 9H AD QD', + '6H 7S JH KH AH 7H TD 5S 6S 2C', + '8H JH 6S 5H 5S 9D TC 4C QC 9S', + '7D 2C KD 3H 5H AS QD 7H JS 4D', + 'TS QH 6C 8H TH 5H 3C 3H 9C 9D', + 'AD KH JS 5D 3H AS AC 9S 5C KC', + '2C KH 8C JC QS 6D AH 2D KC TC', + '9D 3H 2S 7C 4D 6D KH KS 8D 7D', + '9H 2S TC JH AC QC 3H 5S 3S 8H', + '3S AS KD 8H 4C 3H 7C JH QH TS', + '7S 6D 7H 9D JH 4C 3D 3S 6C AS', + '4S 2H 2C 4C 8S 5H KC 8C QC QD', + '3H 3S 6C QS QC 2D 6S 5D 2C 9D', + '2H 8D JH 2S 3H 2D 6C 5C 7S AD', + '9H JS 5D QH 8S TS 2H 7S 6S AD', + '6D QC 9S 7H 5H 5C 7D KC JD 4H', + 'QC 5S 9H 9C 4D 6S KS 2S 4C 7C', + '9H 7C 4H 8D 3S 6H 5C 8H JS 7S', + '2D 6H JS TD 4H 4D JC TH 5H KC', + 'AC 7C 8D TH 3H 9S 2D 4C KC 4D', + 'KD QS 9C 7S 3D KS AD TS 4C 4H', + 'QH 9C 8H 2S 7D KS 7H 5D KD 4C', + '9C 2S 2H JC 6S 6C TC QC JH 5C', + '7S AC 8H KC 8S 6H QS JC 3D 6S', + 'JS 2D JH 8C 4S 6H 8H 6D 5D AD', + '6H 7D 2S 4H 9H 7C AS AC 8H 5S', + '3C JS 4S 6D 5H 2S QH 6S 9C 2C', + '3D 5S 6S 9S 4C QS 8D QD 8S TC', + '9C 3D AH 9H 5S 2C 7D AD JC 3S', + '7H TC AS 3C 6S 6D 7S KH KC 9H', + '3S TC 8H 6S 5H JH 8C 7D AC 2S', + 'QD 9D 9C 3S JC 8C KS 8H 5D 4D', + 'JS AH JD 6D 9D 8C 9H 9S 8H 3H', + '2D 6S 4C 4D 8S AD 4S TC AH 9H', + 'TS AC QC TH KC 6D 4H 7S 8C 2H', + '3C QD JS 9D 5S JC AH 2H TS 9H', + '3H 4D QH 5D 9C 5H 7D 4S JC 3S', + '8S TH 3H 7C 2H JD JS TS AC 8D', + '9C 2H TD KC JD 2S 8C 5S AD 2C', + '3D KD 7C 5H 4D QH QD TC 6H 7D', + '7H 2C KC 5S KD 6H AH QC 7S QH', + '6H 5C AC 5H 2C 9C 2D 7C TD 2S', + '4D 9D AH 3D 7C JD 4H 8C 4C KS', + 'TH 3C JS QH 8H 4C AS 3D QS QC', + '4D 7S 5H JH 6D 7D 6H JS KH 3C', + 'QD 8S 7D 2H 2C 7C JC 2S 5H 8C', + 'QH 8S 9D TC 2H AD 7C 8D QD 6S', + '3S 7C AD 9H 2H 9S JD TS 4C 2D', + '3S AS 4H QC 2C 8H 8S 7S TD TC', + 'JH TH TD 3S 4D 4H 5S 5D QS 2C', + '8C QD QH TC 6D 4S 9S 9D 4H QC', + '8C JS 9D 6H JD 3H AD 6S TD QC', + 'KC 8S 3D 7C TD 7D 8D 9H 4S 3S', + '6C 4S 3D 9D KD TC KC KS AC 5S', + '7C 6S QH 3D JS KD 6H 6D 2D 8C', + 'JD 2S 5S 4H 8S AC 2D 6S TS 5C', + '5H 8C 5S 3C 4S 3D 7C 8D AS 3H', + 'AS TS 7C 3H AD 7D JC QS 6C 6H', + '3S 9S 4C AC QH 5H 5D 9H TS 4H', + '6C 5C 7H 7S TD AD JD 5S 2H 2S', + '7D 6C KC 3S JD 8D 8S TS QS KH', + '8S QS 8D 6C TH AC AH 2C 8H 9S', + '7H TD KH QH 8S 3D 4D AH JD AS', + 'TS 3D 2H JC 2S JH KH 6C QC JS', + 'KC TH 2D 6H 7S 2S TC 8C 9D QS', + '3C 9D 6S KH 8H 6D 5D TH 2C 2H', + '6H TC 7D AD 4D 8S TS 9H TD 7S', + 'JS 6D JD JC 2H AC 6C 3D KH 8D', + 'KH JD 9S 5D 4H 4C 3H 7S QS 5C', + '4H JD 5D 3S 3C 4D KH QH QS 7S', + 'JD TS 8S QD AH 4C 6H 3S 5S 2C', + 'QS 3D JD AS 8D TH 7C 6S QC KS', + '7S 2H 8C QC 7H AC 6D 2D TH KH', + '5S 6C 7H KH 7D AH 8C 5C 7S 3D', + '3C KD AD 7D 6C 4D KS 2D 8C 4S', + '7C 8D 5S 2D 2S AH AD 2C 9D TD', + '3C AD 4S KS JH 7C 5C 8C 9C TH', + 'AS TD 4D 7C JD 8C QH 3C 5H 9S', + '3H 9C 8S 9S 6S QD KS AH 5H JH', + 'QC 9C 5S 4H 2H TD 7D AS 8C 9D', + '8C 2C 9D KD TC 7S 3D KH QC 3C', + '4D AS 4C QS 5S 9D 6S JD QH KS', + '6D AH 6C 4C 5H TS 9H 7D 3D 5S', + 'QS JD 7C 8D 9C AC 3S 6S 6C KH', + '8H JH 5D 9S 6D AS 6S 3S QC 7H', + 'QD AD 5C JH 2H AH 4H AS KC 2C', + 'JH 9C 2C 6H 2D JS 5D 9H KC 6D', + '7D 9D KD TH 3H AS 6S QC 6H AD', + 'JD 4H 7D KC 3H JS 3C TH 3D QS', + '4C 3H 8C QD 5H 6H AS 8H AD JD', + 'TH 8S KD 5D QC 7D JS 5S 5H TS', + '7D KC 9D QS 3H 3C 6D TS 7S AH', + '7C 4H 7H AH QC AC 4D 5D 6D TH', + '3C 4H 2S KD 8H 5H JH TC 6C JD', + '4S 8C 3D 4H JS TD 7S JH QS KD', + '7C QC KD 4D 7H 6S AD TD TC KH', + '5H 9H KC 3H 4D 3D AD 6S QD 6H', + 'TH 7C 6H TS QH 5S 2C KC TD 6S', + '7C 4D 5S JD JH 7D AC KD KH 4H', + '7D 6C 8D 8H 5C JH 8S QD TH JD', + '8D 7D 6C 7C 9D KD AS 5C QH JH', + '9S 2C 8C 3C 4C KS JH 2D 8D 4H', + '7S 6C JH KH 8H 3H 9D 2D AH 6D', + '4D TC 9C 8D 7H TD KS TH KD 3C', + 'JD 9H 8D QD AS KD 9D 2C 2S 9C', + '8D 3H 5C 7H KS 5H QH 2D 8C 9H', + '2D TH 6D QD 6C KC 3H 3S AD 4C', + '4H 3H JS 9D 3C TC 5H QH QC JC', + '3D 5C 6H 3S 3C JC 5S 7S 2S QH', + 'AC 5C 8C 4D 5D 4H 2S QD 3C 3H', + '2C TD AH 9C KD JS 6S QD 4C QC', + 'QS 8C 3S 4H TC JS 3H 7C JC AD', + '5H 4D 9C KS JC TD 9S TS 8S 9H', + 'QD TS 7D AS AC 2C TD 6H 8H AH', + '6S AD 8C 4S 9H 8D 9D KH 8S 3C', + 'QS 4D 2D 7S KH JS JC AD 4C 3C', + 'QS 9S 7H KC TD TH 5H JS AC JH', + '6D AC 2S QS 7C AS KS 6S KH 5S', + '6D 8H KH 3C QS 2H 5C 9C 9D 6C', + 'JS 2C 4C 6H 7D JC AC QD TD 3H', + '4H QC 8H JD 4C KD KS 5C KC 7S', + '6D 2D 3H 2S QD 5S 7H AS TH 6S', + 'AS 6D 8D 2C 8S TD 8H QD JC AH', + '9C 9H 2D TD QH 2H 5C TC 3D 8H', + 'KC 8S 3D KH 2S TS TC 6S 4D JH', + '9H 9D QS AC KC 6H 5D 4D 8D AH', + '9S 5C QS 4H 7C 7D 2H 8S AD JS', + '3D AC 9S AS 2C 2D 2H 3H JC KH', + '7H QH KH JD TC KS 5S 8H 4C 8D', + '2H 7H 3S 2S 5H QS 3C AS 9H KD', + 'AD 3D JD 6H 5S 9C 6D AC 9S 3S', + '3D 5D 9C 2D AC 4S 2S AD 6C 6S', + 'QC 4C 2D 3H 6S KC QH QD 2H JH', + 'QC 3C 8S 4D 9S 2H 5C 8H QS QD', + '6D KD 6S 7H 3S KH 2H 5C JC 6C', + '3S 9S TC 6S 8H 2D AD 7S 8S TS', + '3C 6H 9C 3H 5C JC 8H QH TD QD', + '3C JS QD 5D TD 2C KH 9H TH AS', + '9S TC JD 3D 5C 5H AD QH 9H KC', + 'TC 7H 4H 8H 3H TD 6S AC 7C 2S', + 'QS 9D 5D 3C JC KS 4D 6C JH 2S', + '9S 6S 3C 7H TS 4C KD 6D 3D 9C', + '2D 9H AH AC 7H 2S JH 3S 7C QC', + 'QD 9H 3C 2H AC AS 8S KD 8C KH', + '2D 7S TD TH 6D JD 8D 4D 2H 5S', + '8S QH KD JD QS JH 4D KC 5H 3S', + '3C KH QC 6D 8H 3S AH 7D TD 2D', + '5S 9H QH 4S 6S 6C 6D TS TH 7S', + '6C 4C 6D QS JS 9C TS 3H 8D 8S', + 'JS 5C 7S AS 2C AH 2H AD 5S TC', + 'KD 6C 9C 9D TS 2S JC 4H 2C QD', + 'QS 9H TC 3H KC KS 4H 3C AD TH', + 'KH 9C 2H KD 9D TC 7S KC JH 2D', + '7C 3S KC AS 8C 5D 9C 9S QH 3H', + '2D 8C TD 4C 2H QC 5D TC 2C 7D', + 'KS 4D 6C QH TD KH 5D 7C AD 8D', + '2S 9S 8S 4C 8C 3D 6H QD 7C 7H', + '6C 8S QH 5H TS 5C 3C 4S 2S 2H', + '8S 6S 2H JC 3S 3H 9D 8C 2S 7H', + 'QC 2C 8H 9C AC JD 4C 4H 6S 3S', + '3H 3S 7D 4C 9S 5H 8H JC 3D TC', + 'QH 2S 2D 9S KD QD 9H AD 6D 9C', + '8D 2D KS 9S JC 4C JD KC 4S TH', + 'KH TS 6D 4D 5C KD 5H AS 9H AD', + 'QD JS 7C 6D 5D 5C TH 5H QH QS', + '9D QH KH 5H JH 4C 4D TC TH 6C', + 'KH AS TS 9D KD 9C 7S 4D 8H 5S', + 'KH AS 2S 7D 9D 4C TS TH AH 7C', + 'KS 4D AC 8S 9S 8D TH QH 9D 5C', + '5D 5C 8C QS TC 4C 3D 3S 2C 8D', + '9D KS 2D 3C KC 4S 8C KH 6C JC', + '8H AH 6H 7D 7S QD 3C 4C 6C KC', + '3H 2C QH 8H AS 7D 4C 8C 4H KC', + 'QD 5S 4H 2C TD AH JH QH 4C 8S', + '3H QS 5S JS 8H 2S 9H 9C 3S 2C', + '6H TS 7S JC QD AC TD KC 5S 3H', + 'QH AS QS 7D JC KC 2C 4C 5C 5S', + 'QH 3D AS JS 4H 8D 7H JC 2S 9C', + '5D 4D 2S 4S 9D 9C 2D QS 8H 7H', + '6D 7H 3H JS TS AC 2D JH 7C 8S', + 'JH 5H KC 3C TC 5S 9H 4C 8H 9D', + '8S KC 5H 9H AD KS 9D KH 8D AH', + 'JC 2H 9H KS 6S 3H QC 5H AH 9C', + '5C KH 5S AD 6C JC 9H QC 9C TD', + '5S 5D JC QH 2D KS 8H QS 2H TS', + 'JH 5H 5S AH 7H 3C 8S AS TD KH', + '6H 3D JD 2C 4C KC 7S AH 6C JH', + '4C KS 9D AD 7S KC 7D 8H 3S 9C', + '7H 5C 5H 3C 8H QC 3D KH 6D JC', + '2D 4H 5D 7D QC AD AH 9H QH 8H', + 'KD 8C JS 9D 3S 3C 2H 5D 6D 2S', + '8S 6S TS 3C 6H 8D 5S 3H TD 6C', + 'KS 3D JH 9C 7C 9S QS 5S 4H 6H', + '7S 6S TH 4S KC KD 3S JC JH KS', + '7C 3C 2S 6D QH 2C 7S 5H 8H AH', + 'KC 8D QD 6D KH 5C 7H 9D 3D 9C', + '6H 2D 8S JS 9S 2S 6D KC 7C TC', + 'KD 9C JH 7H KC 8S 2S 7S 3D 6H', + '4H 9H 2D 4C 8H 7H 5S 8S 2H 8D', + 'AD 7C 3C 7S 5S 4D 9H 3D JC KH', + '5D AS 7D 6D 9C JC 4C QH QS KH', + 'KD JD 7D 3D QS QC 8S 6D JS QD', + '6S 8C 5S QH TH 9H AS AC 2C JD', + 'QC KS QH 7S 3C 4C 5C KC 5D AH', + '6C 4H 9D AH 2C 3H KD 3D TS 5C', + 'TD 8S QS AS JS 3H KD AC 4H KS', + '7D 5D TS 9H 4H 4C 9C 2H 8C QC', + '2C 7D 9H 4D KS 4C QH AD KD JS', + 'QD AD AH KH 9D JS 9H JC KD JD', + '8S 3C 4S TS 7S 4D 5C 2S 6H 7C', + 'JS 7S 5C KD 6D QH 8S TD 2H 6S', + 'QH 6C TC 6H TD 4C 9D 2H QC 8H', + '3D TS 4D 2H 6H 6S 2C 7H 8S 6C', + '9H 9D JD JH 3S AH 2C 6S 3H 8S', + '2C QS 8C 5S 3H 2S 7D 3C AD 4S', + '5C QC QH AS TS 4S 6S 4C 5H JS', + 'JH 5C TD 4C 6H JS KD KH QS 4H', + 'TC KH JC 4D 9H 9D 8D KC 3C 8H', + '2H TC 8S AD 9S 4H TS 7H 2C 5C', + '4H 2S 6C 5S KS AH 9C 7C 8H KD', + 'TS QH TD QS 3C JH AH 2C 8D 7D', + '5D KC 3H 5S AC 4S 7H QS 4C 2H', + '3D 7D QC KH JH 6D 6C TD TH KD', + '5S 8D TH 6C 9D 7D KH 8C 9S 6D', + 'JD QS 7S QC 2S QH JC 4S KS 8D', + '7S 5S 9S JD KD 9C JC AD 2D 7C', + '4S 5H AH JH 9C 5D TD 7C 2D 6S', + 'KC 6C 7H 6S 9C QD 5S 4H KS TD', + '6S 8D KS 2D TH TD 9H JD TS 3S', + 'KH JS 4H 5D 9D TC TD QC JD TS', + 'QS QD AC AD 4C 6S 2D AS 3H KC', + '4C 7C 3C TD QS 9C KC AS 8D AD', + 'KC 7H QC 6D 8H 6S 5S AH 7S 8C', + '3S AD 9H JC 6D JD AS KH 6S JH', + 'AD 3D TS KS 7H JH 2D JS QD AC', + '9C JD 7C 6D TC 6H 6C JC 3D 3S', + 'QC KC 3S JC KD 2C 8D AH QS TS', + 'AS KD 3D JD 8H 7C 8C 5C QD 6C' +]; +``` + +## --seed-contents-- + +```js +function pokerHands(arr) { + + return true; +} + +const testArr = [ + '8C TS KC 9H 4S 7D 2S 5D 3S AC', + '5C AD 5D AC 9C 7C 5H 8D TD KS', + '3H 7H 6S KC JS QH TD JC 2D 8S', + 'TH 8H 5C QS TC 9H 4D JC KS JS', + '7C 5H KC QH JD AS KH 4C AD 4S' +]; + +pokerHands(testArr); +``` + +# --solutions-- + +```js +// solution required +``` diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-55-lychrel-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-55-lychrel-numbers.md new file mode 100644 index 00000000000..890c5b0997d --- /dev/null +++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-55-lychrel-numbers.md @@ -0,0 +1,113 @@ +--- +id: 5900f3a31000cf542c50feb6 +title: 'Problem 55: Lychrel numbers' +challengeType: 1 +forumTopicId: 302166 +dashedName: problem-55-lychrel-numbers +--- + +# --description-- + +If we take 47, reverse and add, 47 + 74 = 121, which is palindromic. + +Not all numbers produce palindromes so quickly. For example, + +
+ 349 + 943 = 1292,
+ 1292 + 2921 = 4213
+ 4213 + 3124 = 7337
+
+
+That is, 349 took three iterations to arrive at a palindrome.
+
+Although no one has proved it yet, it is thought that some numbers, like 196, never produce a palindrome. A number that never forms a palindrome through the reverse and add process is called a Lychrel number. Due to the theoretical nature of these numbers, and for the purpose of this problem, we shall assume that a number is Lychrel until proven otherwise. In addition you are given that for every number below ten-thousand, it will either (i) become a palindrome in less than fifty iterations, or, (ii) no one, with all the computing power that exists, has managed so far to map it to a palindrome. In fact, 10677 is the first number to be shown to require over fifty iterations before producing a palindrome: 4668731596684224866951378664 (53 iterations, 28-digits).
+
+Surprisingly, there are palindromic numbers that are themselves Lychrel numbers; the first example is 4994.
+
+How many Lychrel numbers are there below `num`?
+
+**Note:** Wording was modified slightly on 24 April 2007 to emphasize the theoretical nature of Lychrel numbers.
+
+# --hints--
+
+`countLychrelNumbers(1000)` should return a number.
+
+```js
+assert(typeof countLychrelNumbers(1000) === 'number');
+```
+
+`countLychrelNumbers(1000)` should return 13.
+
+```js
+assert.strictEqual(countLychrelNumbers(1000), 13);
+```
+
+`countLychrelNumbers(3243)` should return 39.
+
+```js
+assert.strictEqual(countLychrelNumbers(3243), 39);
+```
+
+`countLychrelNumbers(5000)` should return 76.
+
+```js
+assert.strictEqual(countLychrelNumbers(5000), 76);
+```
+
+`countLychrelNumbers(7654)` should return 140.
+
+```js
+assert.strictEqual(countLychrelNumbers(7654), 140);
+```
+
+`countLychrelNumbers(10000)` should return 249.
+
+```js
+assert.strictEqual(countLychrelNumbers(10000), 249);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function countLychrelNumbers(num) {
+
+ return true;
+}
+
+countLychrelNumbers(10000);
+```
+
+# --solutions--
+
+```js
+const countLychrelNumbers = (size) => {
+ const numReverse = (num) => {
+ return Number(num.toString().split('').reverse().join(''));
+ };
+ const isPalin = (num) => {
+ if (numReverse(num) === num) {
+ return true;
+ }
+ return false;
+ };
+ let total = 0;
+ for (let i = 1; i < size; i++) {
+ let loopCount = 1;
+ let sum = i;
+ while (loopCount < 50) {
+ sum = sum + numReverse(sum);
+ if (isPalin(sum)) {
+ break;
+ } else {
+ loopCount++;
+ }
+ }
+ if (loopCount === 50) {
+ total++;
+ }
+ }
+ return total;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-56-powerful-digit-sum.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-56-powerful-digit-sum.md
new file mode 100644
index 00000000000..e445973f332
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-56-powerful-digit-sum.md
@@ -0,0 +1,101 @@
+---
+id: 5900f3a41000cf542c50feb7
+title: 'Problem 56: Powerful digit sum'
+challengeType: 1
+forumTopicId: 302167
+dashedName: problem-56-powerful-digit-sum
+---
+
+# --description--
+
+A googol ($10^{100}$) is a massive number: one followed by one-hundred zeros; $100^{100}$ is almost unimaginably large: one followed by two-hundred zeros. Despite their size, the sum of the digits in each number is only 1.
+
+Considering natural numbers of the form, $a^b$, where `a`, `b` < `n`, what is the maximum digital sum?
+
+# --hints--
+
+`powerfulDigitSum(3)` should return a number.
+
+```js
+assert(typeof powerfulDigitSum(3) === 'number');
+```
+
+`powerfulDigitSum(3)` should return `4`.
+
+```js
+assert.strictEqual(powerfulDigitSum(3), 4);
+```
+
+`powerfulDigitSum(10)` should return `45`.
+
+```js
+assert.strictEqual(powerfulDigitSum(10), 45);
+```
+
+`powerfulDigitSum(50)` should return `406`.
+
+```js
+assert.strictEqual(powerfulDigitSum(50), 406);
+```
+
+`powerfulDigitSum(75)` should return `684`.
+
+```js
+assert.strictEqual(powerfulDigitSum(75), 684);
+```
+
+`powerfulDigitSum(100)` should return `972`.
+
+```js
+assert.strictEqual(powerfulDigitSum(100), 972);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function powerfulDigitSum(n) {
+
+ return true;
+}
+
+powerfulDigitSum(3);
+```
+
+# --solutions--
+
+```js
+function powerfulDigitSum(n) {
+ function sumDigitsOfPower(numA, numB) {
+ let digitsSum = 0;
+ let number = power(numA, numB);
+ while (number > 0n) {
+ const digit = number % 10n;
+ digitsSum += parseInt(digit, 10);
+ number = number / 10n;
+ }
+ return digitsSum;
+ }
+
+ function power(numA, numB) {
+ let sum = 1n;
+ for (let b = 0; b < numB; b++) {
+ sum = sum * BigInt(numA);
+ }
+ return sum;
+ }
+
+ const limit = n - 1;
+ let maxDigitsSum = 0;
+ for (let a = limit; a > 0; a--) {
+ for (let b = limit; b > 0; b--) {
+ const curDigitSum = sumDigitsOfPower(a, b);
+ if (curDigitSum > maxDigitsSum) {
+ maxDigitsSum = curDigitSum;
+ }
+ }
+ }
+ return maxDigitsSum;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-57-square-root-convergents.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-57-square-root-convergents.md
new file mode 100644
index 00000000000..034974d882c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-57-square-root-convergents.md
@@ -0,0 +1,98 @@
+---
+id: 5900f3a51000cf542c50feb8
+title: 'Problem 57: Square root convergents'
+challengeType: 1
+forumTopicId: 302168
+dashedName: problem-57-square-root-convergents
+---
+
+# --description--
+
+It is possible to show that the square root of two can be expressed as an infinite continued fraction.
+
++ 1292 + 2921 = 4213
+ 4213 + 3124 = 7337
+
$\sqrt 2 =1+ \frac 1 {2+ \frac 1 {2 +\frac 1 {2+ \dots}}}$
+
+By expanding this for the first four iterations, we get:
+
+$1 + \\frac 1 2 = \\frac 32 = 1.5$
+
+$1 + \\frac 1 {2 + \\frac 1 2} = \\frac 7 5 = 1.4$
+
+$1 + \\frac 1 {2 + \\frac 1 {2+\\frac 1 2}} = \\frac {17}{12} = 1.41666 \\dots$
+
+$1 + \\frac 1 {2 + \\frac 1 {2+\\frac 1 {2+\\frac 1 2}}} = \\frac {41}{29} = 1.41379 \\dots$
+
+The next three expansions are $\\frac {99}{70}$, $\\frac {239}{169}$, and $\\frac {577}{408}$, but the eighth expansion, $\\frac {1393}{985}$, is the first example where the number of digits in the numerator exceeds the number of digits in the denominator.
+
+In the first `n` expansions, how many fractions contain a numerator with more digits than denominator?
+
+# --hints--
+
+`squareRootConvergents(10)` should return a number.
+
+```js
+assert(typeof squareRootConvergents(10) === 'number');
+```
+
+`squareRootConvergents(10)` should return 1.
+
+```js
+assert.strictEqual(squareRootConvergents(10), 1);
+```
+
+`squareRootConvergents(100)` should return 15.
+
+```js
+assert.strictEqual(squareRootConvergents(100), 15);
+```
+
+`squareRootConvergents(1000)` should return 153.
+
+```js
+assert.strictEqual(squareRootConvergents(1000), 153);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function squareRootConvergents(n) {
+
+ return true;
+}
+
+squareRootConvergents(1000);
+```
+
+# --solutions--
+
+```js
+function squareRootConvergents(n) {
+ function countDigits(number) {
+ let counter = 0;
+ while (number > 0) {
+ counter++;
+ number = number / 10n;
+ }
+ return counter;
+ }
+
+ // Use BigInt as integer won't handle all cases
+ let numerator = 3n;
+ let denominator = 2n;
+ let moreDigitsInNumerator = 0;
+
+ for (let i = 2; i <= n; i++) {
+ [numerator, denominator] = [
+ numerator + 2n * denominator,
+ denominator + numerator
+ ];
+
+ if (countDigits(numerator) > countDigits(denominator)) {
+ moreDigitsInNumerator++;
+ }
+ }
+ return moreDigitsInNumerator;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-58-spiral-primes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-58-spiral-primes.md
new file mode 100644
index 00000000000..70b80ebf2a1
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-58-spiral-primes.md
@@ -0,0 +1,105 @@
+---
+id: 5900f3a61000cf542c50feb9
+title: 'Problem 58: Spiral primes'
+challengeType: 1
+forumTopicId: 302169
+dashedName: problem-58-spiral-primes
+---
+
+# --description--
+
+Starting with 1 and spiralling anticlockwise in the following way, a square spiral with side length 7 is formed.
+
+
+ 37 36 35 34 33 32 31
+ 38 17 16 15 14 13 30
+ 39 18 5 4 3 12 29
+ 40 19 6 1 2 11 28
+ 41 20 7 8 9 10 27
+ 42 21 22 23 24 25 26
+ 43 44 45 46 47 48 49
+
+
+It is interesting to note that the odd squares lie along the bottom right diagonal, but what is more interesting is that 8 out of the 13 numbers lying along both diagonals are prime; that is, a ratio of 8/13 ≈ 62%.
+
+If one complete new layer is wrapped around the spiral above, a square spiral with side length 9 will be formed. If this process is continued, what is the side length of the square spiral for which the percent of primes along both diagonals first falls below `percent`?
+
+# --hints--
+
+`spiralPrimes(50)` should return a number.
+
+```js
+assert(typeof spiralPrimes(50) === 'number');
+```
+
+`spiralPrimes(50)` should return `11`.
+
+```js
+assert.strictEqual(spiralPrimes(50), 11);
+```
+
+`spiralPrimes(15)` should return `981`.
+
+```js
+assert.strictEqual(spiralPrimes(15), 981);
+```
+
+`spiralPrimes(10)` should return `26241`.
+
+```js
+assert.strictEqual(spiralPrimes(10), 26241);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function spiralPrimes(percent) {
+
+ return true;
+}
+
+spiralPrimes(50);
+```
+
+# --solutions--
+
+```js
+function spiralPrimes(percent) {
+ function isPrime(n) {
+ if (n <= 3) {
+ return n > 1;
+ } else if (n % 2 === 0 || n % 3 === 0) {
+ return false;
+ }
+
+ for (let i = 5; i * i <= n; i += 6) {
+ if (n % i === 0 || n % (i + 2) === 0) {
+ return false;
+ }
+ }
+ return true;
+ }
+
+ let totalCount = 1;
+ let primesCount = 0;
+ let curNumber = 1;
+ let curSideLength = 1;
+ let ratio = 1;
+ const wantedRatio = percent / 100;
+
+ while (ratio >= wantedRatio) {
+ curSideLength += 2;
+ for (let i = 0; i < 4; i++) {
+ curNumber += curSideLength - 1;
+ totalCount++;
+ if (i !== 3 && isPrime(curNumber)) {
+ primesCount++;
+ }
+ }
+ ratio = primesCount / totalCount;
+ }
+ return curSideLength;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-59-xor-decryption.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-59-xor-decryption.md
new file mode 100644
index 00000000000..0784e292908
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-59-xor-decryption.md
@@ -0,0 +1,58 @@
+---
+id: 5900f3a81000cf542c50feba
+title: 'Problem 59: XOR decryption'
+challengeType: 1
+forumTopicId: 302170
+dashedName: problem-59-xor-decryption
+---
+
+# --description--
+
+Each character on a computer is assigned a unique code and the preferred standard is ASCII (American Standard Code for Information Interchange). For example, uppercase A = 65, asterisk (\*) = 42, and lowercase k = 107.
+
+A modern encryption method is to take a text file, convert the bytes to ASCII, then XOR each byte with a given value, taken from a secret key. The advantage with the XOR function is that using the same encryption key on the cipher text, restores the plain text; for example, 65 XOR 42 = 107, then 107 XOR 42 = 65.
+
+For unbreakable encryption, the key is the same length as the plain text message, and the key is made up of random bytes. The user would keep the encrypted message and the encryption key in different locations, and without both "halves", it is impossible to decrypt the message.
+
+Unfortunately, this method is impractical for most users, so the modified method is to use a password as a key. If the password is shorter than the message, which is likely, the key is repeated cyclically throughout the message. The balance for this method is using a sufficiently long password key for security, but short enough to be memorable.
+
+Your task has been made easy, as the encryption key consists of three lower case characters. Using `cipher`, an array containing the encrypted ASCII codes, and the knowledge that the plain text must contain common English words, decrypt the message and find the sum of the ASCII values in the original text.
+
+# --hints--
+
+`XORDecryption(cipher)` should return a number.
+
+```js
+assert(typeof XORDecryption(cipher) === 'number');
+```
+
+`XORDecryption(cipher)` should return 129448.
+
+```js
+assert.strictEqual(XORDecryption(cipher), 129448);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function XORDecryption(arr) {
+
+ return true;
+}
+
+// Only change code above this line
+
+const cipher = [
+ 36,22,80,0,0,4,23,25,19,17,88,4,4,19,21,11,88,22,23,23,29,69,12,24,0,88,25,11,12,2,10,28,5,6,12,25,10,22,80,10,30,80,10,22,21,69,23,22,69,61,5,9,29,2,66,11,80,8,23,3,17,88,19,0,20,21,7,10,17,17,29,20,69,8,17,21,29,2,22,84,80,71,60,21,69,11,5,8,21,25,22,88,3,0,10,25,0,10,5,8,88,2,0,27,25,21,10,31,6,25,2,16,21,82,69,35,63,11,88,4,13,29,80,22,13,29,22,88,31,3,88,3,0,10,25,0,11,80,10,30,80,23,29,19,12,8,2,10,27,17,9,11,45,95,88,57,69,16,17,19,29,80,23,29,19,0,22,4,9,1,80,3,23,5,11,28,92,69,9,5,12,12,21,69,13,30,0,0,0,0,27,4,0,28,28,28,84,80,4,22,80,0,20,21,2,25,30,17,88,21,29,8,2,0,11,3,12,23,30,69,30,31,23,88,4,13,29,80,0,22,4,12,10,21,69,11,5,8,88,31,3,88,4,13,17,3,69,11,21,23,17,21,22,88,65,69,83,80,84,87,68,69,83,80,84,87,73,69,83,80,84,87,65,83,88,91,69,29,4,6,86,92,69,15,24,12,27,24,69,28,21,21,29,30,1,11,80,10,22,80,17,16,21,69,9,5,4,28,2,4,12,5,23,29,80,10,30,80,17,16,21,69,27,25,23,27,28,0,84,80,22,23,80,17,16,17,17,88,25,3,88,4,13,29,80,17,10,5,0,88,3,16,21,80,10,30,80,17,16,25,22,88,3,0,10,25,0,11,80,12,11,80,10,26,4,4,17,30,0,28,92,69,30,2,10,21,80,12,12,80,4,12,80,10,22,19,0,88,4,13,29,80,20,13,17,1,10,17,17,13,2,0,88,31,3,88,4,13,29,80,6,17,2,6,20,21,69,30,31,9,20,31,18,11,94,69,54,17,8,29,28,28,84,80,44,88,24,4,14,21,69,30,31,16,22,20,69,12,24,4,12,80,17,16,21,69,11,5,8,88,31,3,88,4,13,17,3,69,11,21,23,17,21,22,88,25,22,88,17,69,11,25,29,12,24,69,8,17,23,12,80,10,30,80,17,16,21,69,11,1,16,25,2,0,88,31,3,88,4,13,29,80,21,29,2,12,21,21,17,29,2,69,23,22,69,12,24,0,88,19,12,10,19,9,29,80,18,16,31,22,29,80,1,17,17,8,29,4,0,10,80,12,11,80,84,67,80,10,10,80,7,1,80,21,13,4,17,17,30,2,88,4,13,29,80,22,13,29,69,23,22,69,12,24,12,11,80,22,29,2,12,29,3,69,29,1,16,25,28,69,12,31,69,11,92,69,17,4,69,16,17,22,88,4,13,29,80,23,25,4,12,23,80,22,9,2,17,80,70,76,88,29,16,20,4,12,8,28,12,29,20,69,26,9,69,11,80,17,23,80,84,88,31,3,88,4,13,29,80,21,29,2,12,21,21,17,29,2,69,12,31,69,12,24,0,88,20,12,25,29,0,12,21,23,86,80,44,88,7,12,20,28,69,11,31,10,22,80,22,16,31,18,88,4,13,25,4,69,12,24,0,88,3,16,21,80,10,30,80,17,16,25,22,88,3,0,10,25,0,11,80,17,23,80,7,29,80,4,8,0,23,23,8,12,21,17,17,29,28,28,88,65,75,78,68,81,65,67,81,72,70,83,64,68,87,74,70,81,75,70,81,67,80,4,22,20,69,30,2,10,21,80,8,13,28,17,17,0,9,1,25,11,31,80,17,16,25,22,88,30,16,21,18,0,10,80,7,1,80,22,17,8,73,88,17,11,28,80,17,16,21,11,88,4,4,19,25,11,31,80,17,16,21,69,11,1,16,25,2,0,88,2,10,23,4,73,88,4,13,29,80,11,13,29,7,29,2,69,75,94,84,76,65,80,65,66,83,77,67,80,64,73,82,65,67,87,75,72,69,17,3,69,17,30,1,29,21,1,88,0,23,23,20,16,27,21,1,84,80,18,16,25,6,16,80,0,0,0,23,29,3,22,29,3,69,12,24,0,88,0,0,10,25,8,29,4,0,10,80,10,30,80,4,88,19,12,10,19,9,29,80,18,16,31,22,29,80,1,17,17,8,29,4,0,10,80,12,11,80,84,86,80,35,23,28,9,23,7,12,22,23,69,25,23,4,17,30,69,12,24,0,88,3,4,21,21,69,11,4,0,8,3,69,26,9,69,15,24,12,27,24,69,49,80,13,25,20,69,25,2,23,17,6,0,28,80,4,12,80,17,16,25,22,88,3,16,21,92,69,49,80,13,25,6,0,88,20,12,11,19,10,14,21,23,29,20,69,12,24,4,12,80,17,16,21,69,11,5,8,88,31,3,88,4,13,29,80,22,29,2,12,29,3,69,73,80,78,88,65,74,73,70,69,83,80,84,87,72,84,88,91,69,73,95,87,77,70,69,83,80,84,87,70,87,77,80,78,88,21,17,27,94,69,25,28,22,23,80,1,29,0,0,22,20,22,88,31,11,88,4,13,29,80,20,13,17,1,10,17,17,13,2,0,88,31,3,88,4,13,29,80,6,17,2,6,20,21,75,88,62,4,21,21,9,1,92,69,12,24,0,88,3,16,21,80,10,30,80,17,16,25,22,88,29,16,20,4,12,8,28,12,29,20,69,26,9,69,65,64,69,31,25,19,29,3,69,12,24,0,88,18,12,9,5,4,28,2,4,12,21,69,80,22,10,13,2,17,16,80,21,23,7,0,10,89,69,23,22,69,12,24,0,88,19,12,10,19,16,21,22,0,10,21,11,27,21,69,23,22,69,12,24,0,88,0,0,10,25,8,29,4,0,10,80,10,30,80,4,88,19,12,10,19,9,29,80,18,16,31,22,29,80,1,17,17,8,29,4,0,10,80,12,11,80,84,86,80,36,22,20,69,26,9,69,11,25,8,17,28,4,10,80,23,29,17,22,23,30,12,22,23,69,49,80,13,25,6,0,88,28,12,19,21,18,17,3,0,88,18,0,29,30,69,25,18,9,29,80,17,23,80,1,29,4,0,10,29,12,22,21,69,12,24,0,88,3,16,21,3,69,23,22,69,12,24,0,88,3,16,26,3,0,9,5,0,22,4,69,11,21,23,17,21,22,88,25,11,88,7,13,17,19,13,88,4,13,29,80,0,0,0,10,22,21,11,12,3,69,25,2,0,88,21,19,29,30,69,22,5,8,26,21,23,11,94
+];
+
+XORDecryption(cipher);
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-6-sum-square-difference.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-6-sum-square-difference.md
new file mode 100644
index 00000000000..65a460bd803
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-6-sum-square-difference.md
@@ -0,0 +1,78 @@
+---
+id: 5900f3721000cf542c50fe85
+title: 'Problem 6: Sum square difference'
+challengeType: 1
+forumTopicId: 302171
+dashedName: problem-6-sum-square-difference
+---
+
+# --description--
+
+The sum of the squares of the first ten natural numbers is,
+
++ 38 17 16 15 14 13 30
+ 39 18 5 4 3 12 29
+ 40 19 6 1 2 11 28
+ 41 20 7 8 9 10 27
+ 42 21 22 23 24 25 26
+ 43 44 45 46 47 48 49
+
12 + 22 + ... + 102 = 385
+
+The square of the sum of the first ten natural numbers is,
+
+(1 + 2 + ... + 10)2 = 552 = 3025
+
+Hence the difference between the sum of the squares of the first ten natural numbers and the square of the sum is 3025 − 385 = 2640.
+
+Find the difference between the sum of the squares of the first `n` natural numbers and the square of the sum.
+
+# --hints--
+
+`sumSquareDifference(10)` should return a number.
+
+```js
+assert(typeof sumSquareDifference(10) === 'number');
+```
+
+`sumSquareDifference(10)` should return 2640.
+
+```js
+assert.strictEqual(sumSquareDifference(10), 2640);
+```
+
+`sumSquareDifference(20)` should return 41230.
+
+```js
+assert.strictEqual(sumSquareDifference(20), 41230);
+```
+
+`sumSquareDifference(100)` should return 25164150.
+
+```js
+assert.strictEqual(sumSquareDifference(100), 25164150);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumSquareDifference(n) {
+
+ return true;
+}
+
+sumSquareDifference(100);
+```
+
+# --solutions--
+
+```js
+const sumSquareDifference = (number)=>{
+ let squareOfSum = Math.pow(sumOfArithmeticSeries(1,1,number),2);
+ let sumOfSquare = sumOfSquareOfNumbers(number);
+ return squareOfSum - sumOfSquare;
+}
+
+function sumOfArithmeticSeries(a,d,n){
+ return (n/2)*(2*a+(n-1)*d);
+}
+
+function sumOfSquareOfNumbers(n){
+ return (n*(n+1)*(2*n+1))/6;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-60-prime-pair-sets.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-60-prime-pair-sets.md
new file mode 100644
index 00000000000..dc4a88c2cfb
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-60-prime-pair-sets.md
@@ -0,0 +1,46 @@
+---
+id: 5900f3a81000cf542c50febb
+title: 'Problem 60: Prime pair sets'
+challengeType: 1
+forumTopicId: 302172
+dashedName: problem-60-prime-pair-sets
+---
+
+# --description--
+
+The primes 3, 7, 109, and 673, are quite remarkable. By taking any two primes and concatenating them in any order the result will always be prime. For example, taking 7 and 109, both 7109 and 1097 are prime. The sum of these four primes, 792, represents the lowest sum for a set of four primes with this property.
+
+Find the lowest sum for a set of five primes for which any two primes concatenate to produce another prime.
+
+# --hints--
+
+`primePairSets()` should return a number.
+
+```js
+assert(typeof primePairSets() === 'number');
+```
+
+`primePairSets()` should return 26033.
+
+```js
+assert.strictEqual(primePairSets(), 26033);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primePairSets() {
+
+ return true;
+}
+
+primePairSets();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-61-cyclical-figurate-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-61-cyclical-figurate-numbers.md
new file mode 100644
index 00000000000..99fee7255e8
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-61-cyclical-figurate-numbers.md
@@ -0,0 +1,252 @@
+---
+id: 5900f3a91000cf542c50febc
+title: 'Problem 61: Cyclical figurate numbers'
+challengeType: 1
+forumTopicId: 302173
+dashedName: problem-61-cyclical-figurate-numbers
+---
+
+# --description--
+
+Triangle, square, pentagonal, hexagonal, heptagonal, and octagonal numbers are all figurate (polygonal) numbers and are generated by the following formulae:
+
+| Type of Number | Formula | Sequence |
+| -------------- | ----------------------------- | --------------------- |
+| Triangle | $P_3(n) = \frac{n(n+1)}{2}$ | 1, 3, 6, 10, 15, ... |
+| Square | $P_4(n) = n^2$ | 1, 4, 9, 16, 25, ... |
+| Pentagonal | $P_5(n) = \frac{n(3n−1)}2$ | 1, 5, 12, 22, 35, ... |
+| Hexagonal | $P_6(n) = n(2n−1)$ | 1, 6, 15, 28, 45, ... |
+| Heptagonal | $P_7(n) = \frac{n(5n−3)}{2}$ | 1, 7, 18, 34, 55, ... |
+| Octagonal | $P_8(n) = n(3n−2)$ | 1, 8, 21, 40, 65, ... |
+
+The ordered set of three 4-digit numbers: 8128, 2882, 8281, has three interesting properties.
+
+1. The set is cyclic, in that the last two digits of each number is the first two digits of the next number (including the last number with the first).
+2. Each polygonal type: triangle ($P_3(127) = 8128$), square ($P_4(91) = 8281$), and pentagonal ($P_5(44) = 2882$), is represented by a different number in the set.
+3. This is the only set of 4-digit numbers with this property.
+
+Find the sum of all numbers in ordered sets of `n` cyclic 4-digit numbers for which each of the $P_3$ to $P_{n + 2}$ polygonal types, is represented by a different number in the set.
+
+# --hints--
+
+`cyclicalFigurateNums(3)` should return a number.
+
+```js
+assert(typeof cyclicalFigurateNums(3) === 'number');
+```
+
+`cyclicalFigurateNums(3)` should return `19291`.
+
+```js
+assert.strictEqual(cyclicalFigurateNums(3), 19291);
+```
+
+`cyclicalFigurateNums(4)` should return `28684`.
+
+```js
+assert.strictEqual(cyclicalFigurateNums(4), 28684);
+```
+
+`cyclicalFigurateNums(5)` should return `76255`.
+
+```js
+assert.strictEqual(cyclicalFigurateNums(5), 76255);
+```
+
+`cyclicalFigurateNums(6)` should return `28684`.
+
+```js
+assert.strictEqual(cyclicalFigurateNums(6), 28684);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function cyclicalFigurateNums(n) {
+
+ return true;
+}
+
+cyclicalFigurateNums(3);
+```
+
+# --solutions--
+
+```js
+function cyclicalFigurateNums(n) {
+ function getChains(chain, n, numberTypes, numsExcludingLastNeededType) {
+ if (chain.length === n) {
+ return [chain];
+ }
+
+ const nextNumbers = getNextNumbersInChain(
+ chain[chain.length - 1],
+ numsExcludingLastNeededType
+ );
+
+ const chains = [];
+ for (let j = 0; j < nextNumbers.length; j++) {
+ const nextNumber = nextNumbers[j];
+ if (chain.indexOf(nextNumber) === -1) {
+ const nextChain = [...chain, nextNumber];
+ chains.push(
+ ...getChains(nextChain, n, numberTypes, numsExcludingLastNeededType)
+ );
+ }
+ }
+ return chains;
+ }
+
+ function getNextNumbersInChain(num, numsExcludingLastNeededType) {
+ const results = [];
+ const beginning = num % 100;
+ numsExcludingLastNeededType.forEach(number => {
+ if (Math.floor(number / 100) === beginning) {
+ results.push(number);
+ }
+ });
+ return results;
+ }
+
+ function fillNumberTypes(n, numberTypes, numsExcludingLastNeededType) {
+ const [, lastTypeCheck, lastTypeArr] = numberTypes[n - 1];
+
+ for (let i = 1000; i <= 9999; i++) {
+ for (let j = 0; j < n - 1; j++) {
+ const [, typeCheck, typeArr] = numberTypes[j];
+ if (typeCheck(i)) {
+ typeArr.push(i);
+ numsExcludingLastNeededType.add(i);
+ }
+ }
+
+ if (lastTypeCheck(i)) {
+ lastTypeArr.push(i);
+ }
+ }
+ }
+
+ function isCyclicalChain(chain, n, numberTypes) {
+ const numberTypesInChain = getNumberTypesInChain(chain, numberTypes);
+
+ if (!isChainAllowed(numberTypesInChain, n)) {
+ return false;
+ }
+
+ const isChainCyclic =
+ Math.floor(chain[0] / 100) === chain[chain.length - 1] % 100;
+ return isChainCyclic;
+ }
+
+ function getNumberTypesInChain(chain, numberTypes) {
+ const numbersInChain = {};
+ for (let i = 0; i < numberTypes.length; i++) {
+ const numberTypeName = numberTypes[i][0];
+ numbersInChain[numberTypeName] = [];
+ }
+
+ for (let i = 0; i < chain.length; i++) {
+ for (let j = 0; j < n; j++) {
+ const [typeName, , typeNumbers] = numberTypes[j];
+ const typeNumbersInChain = numbersInChain[typeName];
+ if (typeNumbers.indexOf(chain[i]) !== -1) {
+ typeNumbersInChain.push(chain[i]);
+ }
+ }
+ }
+ return numbersInChain;
+ }
+
+ function isChainAllowed(numberTypesInChain, n) {
+ for (let i = 0; i < n; i++) {
+ const typeName = numberTypes[i][0];
+ const isNumberWithTypeInChain = numberTypesInChain[typeName].length > 0;
+ if (!isNumberWithTypeInChain) {
+ return false;
+ }
+
+ for (let j = i + 1; j < n; j++) {
+ const otherTypeName = numberTypes[j][0];
+ if (
+ isNumberRepeatedAsOnlyNumberInTwoTypes(
+ numberTypesInChain[typeName],
+ numberTypesInChain[otherTypeName]
+ )
+ ) {
+ return false;
+ }
+ }
+ }
+ return true;
+ }
+
+ function isNumberRepeatedAsOnlyNumberInTwoTypes(
+ typeNumbers,
+ otherTypeNumbers
+ ) {
+ return (
+ typeNumbers.length === 1 &&
+ otherTypeNumbers.length === 1 &&
+ typeNumbers[0] === otherTypeNumbers[0]
+ );
+ }
+
+ function isTriangle(num) {
+ return ((8 * num + 1) ** 0.5 - 1) % 2 === 0;
+ }
+
+ function isSquare(num) {
+ return num ** 0.5 === parseInt(num ** 0.5, 10);
+ }
+
+ function isPentagonal(num) {
+ return ((24 * num + 1) ** 0.5 + 1) % 6 === 0;
+ }
+
+ function isHexagonal(num) {
+ return ((8 * num + 1) ** 0.5 + 1) % 4 === 0;
+ }
+
+ function isHeptagonal(num) {
+ return ((40 * num + 9) ** 0.5 + 3) % 10 === 0;
+ }
+
+ function isOctagonal(num) {
+ return ((3 * num + 1) ** 0.5 + 1) % 3 === 0;
+ }
+
+ const numberTypes = [
+ ['triangle', isTriangle, []],
+ ['square', isSquare, []],
+ ['pentagonal', isPentagonal, []],
+ ['hexagonal', isHexagonal, []],
+ ['heptagonal', isHeptagonal, []],
+ ['octagonal', isOctagonal, []]
+ ];
+ const numsExcludingLastNeededType = new Set();
+ fillNumberTypes(n, numberTypes, numsExcludingLastNeededType);
+
+ const nNumberChains = [];
+ const [, , lastType] = numberTypes[n - 1];
+ for (let i = 0; i < lastType.length; i++) {
+ const startOfChain = lastType[i];
+ nNumberChains.push(
+ ...getChains([startOfChain], n, numberTypes, numsExcludingLastNeededType)
+ );
+ }
+
+ const cyclicalChains = nNumberChains.filter(chain =>
+ isCyclicalChain(chain, n, numberTypes)
+ );
+
+ let sum = 0;
+ for (let i = 0; i < cyclicalChains.length; i++) {
+ for (let j = 0; j < cyclicalChains[0].length; j++) {
+ sum += cyclicalChains[i][j];
+ }
+ }
+ return sum;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-62-cubic-permutations.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-62-cubic-permutations.md
new file mode 100644
index 00000000000..a89d136f83c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-62-cubic-permutations.md
@@ -0,0 +1,97 @@
+---
+id: 5900f3aa1000cf542c50febd
+title: 'Problem 62: Cubic permutations'
+challengeType: 1
+forumTopicId: 302174
+dashedName: problem-62-cubic-permutations
+---
+
+# --description--
+
+The cube, 41063625 ($345^3$), can be permuted to produce two other cubes: 56623104 ($384^3$) and 66430125 ($405^3$). In fact, 41063625 is the smallest cube which has exactly three permutations of its digits which are also cube.
+
+Find the smallest cube for which exactly `n` permutations of its digits are cube.
+
+# --hints--
+
+`cubicPermutations(2)` should return a number.
+
+```js
+assert(typeof cubicPermutations(2) === 'number');
+```
+
+`cubicPermutations(2)` should return `125`.
+
+```js
+assert.strictEqual(cubicPermutations(2), 125);
+```
+
+`cubicPermutations(3)` should return `41063625`.
+
+```js
+assert.strictEqual(cubicPermutations(3), 41063625);
+```
+
+`cubicPermutations(4)` should return `1006012008`.
+
+```js
+assert.strictEqual(cubicPermutations(4), 1006012008);
+```
+
+`cubicPermutations(5)` should return `127035954683`.
+
+```js
+assert.strictEqual(cubicPermutations(5), 127035954683);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function cubicPermutations(n) {
+
+ return true;
+}
+
+cubicPermutations(2);
+```
+
+# --solutions--
+
+```js
+function cubicPermutations(n) {
+ function getDigits(num) {
+ const digits = [];
+ while (num > 0) {
+ digits.push(num % 10);
+ num = Math.floor(num / 10);
+ }
+ return digits;
+ }
+
+ function getCube(num) {
+ return num ** 3;
+ }
+
+ const digitsToCubeCounts = {};
+ let curNum = 1;
+ let digits;
+
+ while (!digitsToCubeCounts[digits] || digitsToCubeCounts[digits].count < n) {
+ const cube = getCube(curNum);
+ digits = getDigits(cube).sort().join();
+ if (!digitsToCubeCounts[digits]) {
+ digitsToCubeCounts[digits] = {
+ count: 1,
+ smallestCube: cube
+ };
+ } else {
+ digitsToCubeCounts[digits].count += 1;
+ }
+
+ curNum++;
+ }
+ return digitsToCubeCounts[digits].smallestCube;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-63-powerful-digit-counts.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-63-powerful-digit-counts.md
new file mode 100644
index 00000000000..2c8b0bb8cd6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-63-powerful-digit-counts.md
@@ -0,0 +1,122 @@
+---
+id: 5900f3ab1000cf542c50febe
+title: 'Problem 63: Powerful digit counts'
+challengeType: 1
+forumTopicId: 302175
+dashedName: problem-63-powerful-digit-counts
+---
+
+# --description--
+
+The 5-digit number, 16807 = 75, is also a fifth power. Similarly, the 9-digit number, 134217728 = 89, is a ninth power.
+
+Complete the function so that it returns how many positive integers are of length `n` and an `n`th power.
+
+# --hints--
+
+`powerfulDigitCounts(1)` should return a number.
+
+```js
+assert(typeof powerfulDigitCounts(1) === 'number');
+```
+
+`powerfulDigitCounts(1)` should return `9`.
+
+```js
+assert.strictEqual(powerfulDigitCounts(1), 9);
+```
+
+`powerfulDigitCounts(2)` should return `6`.
+
+```js
+assert.strictEqual(powerfulDigitCounts(2), 6);
+```
+
+`powerfulDigitCounts(3)` should return `5`.
+
+```js
+assert.strictEqual(powerfulDigitCounts(3), 5);
+```
+
+`powerfulDigitCounts(4)` should return `4`.
+
+```js
+assert.strictEqual(powerfulDigitCounts(4), 4);
+```
+
+`powerfulDigitCounts(5)` should return `3`.
+
+```js
+assert.strictEqual(powerfulDigitCounts(5), 3);
+```
+
+`powerfulDigitCounts(6)` should return `3`.
+
+```js
+assert.strictEqual(powerfulDigitCounts(6), 3);
+```
+
+`powerfulDigitCounts(7)` should return `2`.
+
+```js
+assert.strictEqual(powerfulDigitCounts(7), 2);
+```
+
+`powerfulDigitCounts(8)` should return `2`.
+
+```js
+assert.strictEqual(powerfulDigitCounts(8), 2);
+```
+
+`powerfulDigitCounts(10)` should return `2`.
+
+```js
+assert.strictEqual(powerfulDigitCounts(10), 2);
+```
+
+`powerfulDigitCounts(21)` should return `1`.
+
+```js
+assert.strictEqual(powerfulDigitCounts(21), 1);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function powerfulDigitCounts(n) {
+
+ return true;
+}
+
+powerfulDigitCounts(1);
+```
+
+# --solutions--
+
+```js
+function powerfulDigitCounts(n) {
+ function countDigits(num) {
+ let counter = 0;
+ while (num > 0) {
+ num = Math.floor(num / 10);
+ counter++;
+ }
+ return counter;
+ }
+
+ let numbersCount = 0;
+
+ let curNum = 1;
+ while (curNum < 10) {
+ let power = n;
+ if (power === countDigits(curNum ** power)) {
+ numbersCount++;
+ }
+ curNum++;
+ }
+
+ return numbersCount;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-64-odd-period-square-roots.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-64-odd-period-square-roots.md
new file mode 100644
index 00000000000..a6acdfc610e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-64-odd-period-square-roots.md
@@ -0,0 +1,148 @@
+---
+id: 5900f3ac1000cf542c50febf
+title: 'Problem 64: Odd period square roots'
+challengeType: 1
+forumTopicId: 302176
+dashedName: problem-64-odd-period-square-roots
+---
+
+# --description--
+
+All square roots are periodic when written as continued fractions and can be written in the form:
+
+$\\displaystyle \\quad \\quad \\sqrt{N}=a_0+\\frac 1 {a_1+\\frac 1 {a_2+ \\frac 1 {a3+ \\dots}}}$
+
+For example, let us consider $\\sqrt{23}$:
+
+$\\quad \\quad \\sqrt{23}=4+\\sqrt{23}-4=4+\\frac 1 {\\frac 1 {\\sqrt{23}-4}}=4+\\frac 1 {1+\\frac{\\sqrt{23}-3}7}$
+
+If we continue we would get the following expansion:
+
+$\\displaystyle \\quad \\quad \\sqrt{23}=4+\\frac 1 {1+\\frac 1 {3+ \\frac 1 {1+\\frac 1 {8+ \\dots}}}}$
+
+The process can be summarized as follows:
+
+$\\quad \\quad a_0=4, \\frac 1 {\\sqrt{23}-4}=\\frac {\\sqrt{23}+4} 7=1+\\frac {\\sqrt{23}-3} 7$
+
+$\\quad \\quad a_1=1, \\frac 7 {\\sqrt{23}-3}=\\frac {7(\\sqrt{23}+3)} {14}=3+\\frac {\\sqrt{23}-3} 2$
+
+$\\quad \\quad a_2=3, \\frac 2 {\\sqrt{23}-3}=\\frac {2(\\sqrt{23}+3)} {14}=1+\\frac {\\sqrt{23}-4} 7$
+
+$\\quad \\quad a_3=1, \\frac 7 {\\sqrt{23}-4}=\\frac {7(\\sqrt{23}+4)} 7=8+\\sqrt{23}-4$
+
+$\\quad \\quad a_4=8, \\frac 1 {\\sqrt{23}-4}=\\frac {\\sqrt{23}+4} 7=1+\\frac {\\sqrt{23}-3} 7$
+
+$\\quad \\quad a_5=1, \\frac 7 {\\sqrt{23}-3}=\\frac {7 (\\sqrt{23}+3)} {14}=3+\\frac {\\sqrt{23}-3} 2$
+
+$\\quad \\quad a_6=3, \\frac 2 {\\sqrt{23}-3}=\\frac {2(\\sqrt{23}+3)} {14}=1+\\frac {\\sqrt{23}-4} 7$
+
+$\\quad \\quad a_7=1, \\frac 7 {\\sqrt{23}-4}=\\frac {7(\\sqrt{23}+4)} {7}=8+\\sqrt{23}-4$
+
+It can be seen that the sequence is repeating. For conciseness, we use the notation $\\sqrt{23}=\[4;(1,3,1,8)]$, to indicate that the block (1,3,1,8) repeats indefinitely.
+
+The first ten continued fraction representations of (irrational) square roots are:
+
+$\\quad \\quad \\sqrt{2}=\[1;(2)]$, period = 1
+
+$\\quad \\quad \\sqrt{3}=\[1;(1,2)]$, period = 2
+
+$\\quad \\quad \\sqrt{5}=\[2;(4)]$, period = 1
+
+$\\quad \\quad \\sqrt{6}=\[2;(2,4)]$, period = 2
+
+$\\quad \\quad \\sqrt{7}=\[2;(1,1,1,4)]$, period = 4
+
+$\\quad \\quad \\sqrt{8}=\[2;(1,4)]$, period = 2
+
+$\\quad \\quad \\sqrt{10}=\[3;(6)]$, period = 1
+
+$\\quad \\quad \\sqrt{11}=\[3;(3,6)]$, period = 2
+
+$\\quad \\quad \\sqrt{12}=\[3;(2,6)]$, period = 2
+
+$\\quad \\quad \\sqrt{13}=\[3;(1,1,1,1,6)]$, period = 5
+
+Exactly four continued fractions, for $N \\le 13$, have an odd period.
+
+How many continued fractions for $N \\le n$ have an odd period?
+
+# --hints--
+
+`oddPeriodSqrts(13)` should return a number.
+
+```js
+assert(typeof oddPeriodSqrts(13) === 'number');
+```
+
+`oddPeriodSqrts(500)` should return `83`.
+
+```js
+assert.strictEqual(oddPeriodSqrts(500), 83);
+```
+
+`oddPeriodSqrts(1000)` should return `152`.
+
+```js
+assert.strictEqual(oddPeriodSqrts(1000), 152);
+```
+
+`oddPeriodSqrts(5000)` should return `690`.
+
+```js
+assert.strictEqual(oddPeriodSqrts(5000), 690);
+```
+
+`oddPeriodSqrts(10000)` should return `1322`.
+
+```js
+assert.strictEqual(oddPeriodSqrts(10000), 1322);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function oddPeriodSqrts(n) {
+
+ return true;
+}
+
+oddPeriodSqrts(13);
+```
+
+# --solutions--
+
+```js
+function oddPeriodSqrts(n) {
+ // Based on https://www.mathblog.dk/project-euler-continued-fractions-odd-period/
+ function getPeriod(num) {
+ let period = 0;
+ let m = 0;
+ let d = 1;
+ let a = Math.floor(Math.sqrt(num));
+ const a0 = a;
+ while (2 * a0 !== a) {
+ m = d * a - m;
+ d = Math.floor((num - m ** 2) / d);
+ a = Math.floor((Math.sqrt(num) + m) / d);
+ period++;
+ }
+ return period;
+ }
+
+ function isPerfectSquare(num) {
+ return Number.isInteger(Math.sqrt(num));
+ }
+
+ let counter = 0;
+ for (let i = 2; i <= n; i++) {
+ if (!isPerfectSquare(i)) {
+ if (getPeriod(i) % 2 !== 0) {
+ counter++;
+ }
+ }
+ }
+ return counter;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-65-convergents-of-e.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-65-convergents-of-e.md
new file mode 100644
index 00000000000..9aa62302442
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-65-convergents-of-e.md
@@ -0,0 +1,117 @@
+---
+id: 5900f3ad1000cf542c50fec0
+title: 'Problem 65: Convergents of e'
+challengeType: 1
+forumTopicId: 302177
+dashedName: problem-65-convergents-of-e
+---
+
+# --description--
+
+The square root of 2 can be written as an infinite continued fraction.
+
+$\\sqrt{2} = 1 + \\dfrac{1}{2 + \\dfrac{1}{2 + \\dfrac{1}{2 + \\dfrac{1}{2 + ...}}}}$
+
+The infinite continued fraction can be written, $\\sqrt{2} = \[1; (2)]$ indicates that 2 repeats *ad infinitum*. In a similar way, $\\sqrt{23} = \[4; (1, 3, 1, 8)]$. It turns out that the sequence of partial values of continued fractions for square roots provide the best rational approximations. Let us consider the convergents for $\\sqrt{2}$.
+
+$1 + \\dfrac{1}{2} = \\dfrac{3}{2}\\\\ 1 + \\dfrac{1}{2 + \\dfrac{1}{2}} = \\dfrac{7}{5}\\\\ 1 + \\dfrac{1}{2 + \\dfrac{1}{2 + \\dfrac{1}{2}}} = \\dfrac{17}{12}\\\\ 1 + \\dfrac{1}{2 + \\dfrac{1}{2 + \\dfrac{1}{2 + \\dfrac{1}{2}}}} = \\dfrac{41}{29}$
+
+Hence the sequence of the first ten convergents for $\\sqrt{2}$ are:
+
+$1, \\dfrac{3}{2}, \\dfrac{7}{5}, \\dfrac{17}{12}, \\dfrac{41}{29}, \\dfrac{99}{70}, \\dfrac{239}{169}, \\dfrac{577}{408}, \\dfrac{1393}{985}, \\dfrac{3363}{2378}, ...$
+
+What is most surprising is that the important mathematical constant, $e = \[2; 1, 2, 1, 1, 4, 1, 1, 6, 1, ... , 1, 2k, 1, ...]$. The first ten terms in the sequence of convergents for `e` are:
+
+$2, 3, \\dfrac{8}{3}, \\dfrac{11}{4}, \\dfrac{19}{7}, \\dfrac{87}{32}, \\dfrac{106}{39}, \\dfrac{193}{71}, \\dfrac{1264}{465}, \\dfrac{1457}{536}, ...$
+
+The sum of digits in the numerator of the 10th convergent is $1 + 4 + 5 + 7 = 17$.
+
+Find the sum of digits in the numerator of the `n`th convergent of the continued fraction for `e`.
+
+# --hints--
+
+`convergentsOfE(10)` should return a number.
+
+```js
+assert(typeof convergentsOfE(10) === 'number');
+```
+
+`convergentsOfE(10)` should return `17`.
+
+```js
+assert.strictEqual(convergentsOfE(10), 17);
+```
+
+`convergentsOfE(30)` should return `53`.
+
+```js
+assert.strictEqual(convergentsOfE(30), 53);
+```
+
+`convergentsOfE(50)` should return `91`.
+
+```js
+assert.strictEqual(convergentsOfE(50), 91);
+```
+
+`convergentsOfE(70)` should return `169`.
+
+```js
+assert.strictEqual(convergentsOfE(70), 169);
+```
+
+`convergentsOfE(100)` should return `272`.
+
+```js
+assert.strictEqual(convergentsOfE(100), 272);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function convergentsOfE(n) {
+
+ return true;
+}
+
+convergentsOfE(10);
+```
+
+# --solutions--
+
+```js
+function convergentsOfE(n) {
+ function sumDigits(num) {
+ let sum = 0n;
+ while (num > 0) {
+ sum += num % 10n;
+ num = num / 10n;
+ }
+ return parseInt(sum);
+ }
+
+ // BigInt is needed for high convergents
+ let convergents = [
+ [2n, 1n],
+ [3n, 1n]
+ ];
+ const multipliers = [1n, 1n, 2n];
+ for (let i = 2; i < n; i++) {
+ const [secondLastConvergent, lastConvergent] = convergents;
+ const [secondLastNumerator, secondLastDenominator] = secondLastConvergent;
+ const [lastNumerator, lastDenominator] = lastConvergent;
+ const curMultiplier = multipliers[i % 3];
+
+ const numerator = secondLastNumerator + curMultiplier * lastNumerator;
+ const denominator = secondLastDenominator + curMultiplier * lastDenominator;
+
+ convergents = [lastConvergent, [numerator, denominator]]
+ if (i % 3 === 2) {
+ multipliers[2] += 2n;
+ }
+ }
+ return sumDigits(convergents[1][0]);
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-66-diophantine-equation.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-66-diophantine-equation.md
new file mode 100644
index 00000000000..9e01ce1b0c5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-66-diophantine-equation.md
@@ -0,0 +1,129 @@
+---
+id: 5900f3ae1000cf542c50fec1
+title: 'Problem 66: Diophantine equation'
+challengeType: 1
+forumTopicId: 302178
+dashedName: problem-66-diophantine-equation
+---
+
+# --description--
+
+Consider quadratic Diophantine equations of the form:
+
+x2 – Dy2 = 1
+
+For example, when D=13, the minimal solution in x is 6492 – 13×1802 = 1.
+
+It can be assumed that there are no solutions in positive integers when D is square.
+
+By finding minimal solutions in x for D = {2, 3, 5, 6, 7}, we obtain the following:
+
+
+ 32 – 2×22 = 1
+ 22 – 3×12 = 1
+ 92 – 5×42 = 1
+ 52 – 6×22 = 1
+ 82 – 7×32 = 1
+
+
+Hence, by considering minimal solutions in `x` for D ≤ 7, the largest `x` is obtained when D=5.
+
+Find the value of D ≤ `n` in minimal solutions of `x` for which the largest value of `x` is obtained.
+
+# --hints--
+
+`diophantineEquation(7)` should return a number.
+
+```js
+assert(typeof diophantineEquation(7) === 'number');
+```
+
+`diophantineEquation(7)` should return `5`.
+
+```js
+assert.strictEqual(diophantineEquation(7), 5);
+```
+
+`diophantineEquation(100)` should return `61`.
+
+```js
+assert.strictEqual(diophantineEquation(100), 61);
+```
+
+`diophantineEquation(409)` should return `409`.
+
+```js
+assert.strictEqual(diophantineEquation(409), 409);
+```
+
+`diophantineEquation(500)` should return `421`.
+
+```js
+assert.strictEqual(diophantineEquation(500), 421);
+```
+
+`diophantineEquation(1000)` should return `661`.
+
+```js
+assert.strictEqual(diophantineEquation(1000), 661);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function diophantineEquation(n) {
+
+ return true;
+}
+
+diophantineEquation(7);
+```
+
+# --solutions--
+
+```js
+function diophantineEquation(n) {
+ // Based on https://www.mathblog.dk/project-euler-66-diophantine-equation/
+ function isSolution(D, numerator, denominator) {
+ return numerator * numerator - BigInt(D) * denominator * denominator === 1n;
+ }
+
+ let result = 0;
+ let biggestX = 0;
+
+ for (let D = 2; D <= n; D++) {
+ let boundary = Math.floor(Math.sqrt(D));
+ if (boundary ** 2 === D) {
+ continue;
+ }
+
+ let m = 0n;
+ let d = 1n;
+ let a = BigInt(boundary);
+
+ let [numerator, prevNumerator] = [a, 1n];
+
+ let [denominator, prevDenominator] = [1n, 0n];
+
+ while (!isSolution(D, numerator, denominator)) {
+ m = d * a - m;
+ d = (BigInt(D) - m * m) / d;
+ a = (BigInt(boundary) + m) / d;
+
+ [numerator, prevNumerator] = [a * numerator + prevNumerator, numerator];
+ [denominator, prevDenominator] = [
+ a * denominator + prevDenominator,
+ denominator
+ ];
+ }
+
+ if (numerator > biggestX) {
+ biggestX = numerator;
+ result = D;
+ }
+ }
+ return result;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-67-maximum-path-sum-ii.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-67-maximum-path-sum-ii.md
new file mode 100644
index 00000000000..c3aa2fb6e3b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-67-maximum-path-sum-ii.md
@@ -0,0 +1,96 @@
+---
+id: 5900f3b01000cf542c50fec2
+title: 'Problem 67: Maximum path sum II'
+challengeType: 1
+forumTopicId: 302179
+dashedName: problem-67-maximum-path-sum-ii
+---
+
+# --description--
+
+By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.
+
++ 22 – 3×12 = 1
+ 92 – 5×42 = 1
+ 52 – 6×22 = 1
+ 82 – 7×32 = 1
+
+ 3
+ 7 4
+ 2 4 6
+ 8 5 9 3 +
+
+That is, 3 + 7 + 4 + 9 = 23.
+
+Find the maximum total from top to bottom in `numTriangle`, a 2D array defined in the background containing a triangle with one-hundred rows.
+
+**Note:** This is a much more difficult version of Problem 18. It is not possible to try every route to solve this problem, as there are 299 altogether! If you could check one trillion (1012) routes every second it would take over twenty billion years to check them all. There is an efficient algorithm to solve it. ;o)
+
+# --hints--
+
+`maximumPathSumII(testTriangle)` should return a number.
+
+```js
+assert(typeof maximumPathSumII(_testTriangle) === 'number');
+```
+
+`maximumPathSumII(testTriangle)` should return 23.
+
+```js
+assert.strictEqual(maximumPathSumII(_testTriangle), 23);
+```
+
+`maximumPathSumII(numTriangle)` should return 7273.
+
+```js
+assert.strictEqual(maximumPathSumII(_numTriangle), 7273);
+```
+
+# --seed--
+
+## --before-user-code--
+
+```js
+const _testTriangle = [[3, 0, 0, 0],
+ [7, 4, 0, 0],
+ [2, 4, 6, 0],
+ [8, 5, 9, 3]];
+const _numTriangle = [[59,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[73,41,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[52,40,9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[26,53,6,34,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[10,51,87,86,81,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[61,95,66,57,25,68,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[90,81,80,38,92,67,73,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[30,28,51,76,81,18,75,44,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[84,14,95,87,62,81,17,78,58,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[21,46,71,58,2,79,62,39,31,9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[56,34,35,53,78,31,81,18,90,93,15,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[78,53,4,21,84,93,32,13,97,11,37,51,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[45,3,81,79,5,18,78,86,13,30,63,99,95,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[39,87,96,28,3,38,42,17,82,87,58,7,22,57,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[6,17,51,17,7,93,9,7,75,97,95,78,87,8,53,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[67,66,59,60,88,99,94,65,55,77,55,34,27,53,78,28,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[76,40,41,4,87,16,9,42,75,69,23,97,30,60,10,79,87,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[12,10,44,26,21,36,32,84,98,60,13,12,36,16,63,31,91,35,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[70,39,6,5,55,27,38,48,28,22,34,35,62,62,15,14,94,89,86,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[66,56,68,84,96,21,34,34,34,81,62,40,65,54,62,5,98,3,2,60,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[38,89,46,37,99,54,34,53,36,14,70,26,2,90,45,13,31,61,83,73,47,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[36,10,63,96,60,49,41,5,37,42,14,58,84,93,96,17,9,43,5,43,6,59,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[66,57,87,57,61,28,37,51,84,73,79,15,39,95,88,87,43,39,11,86,77,74,18,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[54,42,5,79,30,49,99,73,46,37,50,2,45,9,54,52,27,95,27,65,19,45,26,45,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[71,39,17,78,76,29,52,90,18,99,78,19,35,62,71,19,23,65,93,85,49,33,75,9,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[33,24,47,61,60,55,32,88,57,55,91,54,46,57,7,77,98,52,80,99,24,25,46,78,79,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[92,9,13,55,10,67,26,78,76,82,63,49,51,31,24,68,5,57,7,54,69,21,67,43,17,63,12,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[24,59,6,8,98,74,66,26,61,60,13,3,9,9,24,30,71,8,88,70,72,70,29,90,11,82,41,34,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[66,82,67,4,36,60,92,77,91,85,62,49,59,61,30,90,29,94,26,41,89,4,53,22,83,41,9,74,90,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[48,28,26,37,28,52,77,26,51,32,18,98,79,36,62,13,17,8,19,54,89,29,73,68,42,14,8,16,70,37,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[37,60,69,70,72,71,9,59,13,60,38,13,57,36,9,30,43,89,30,39,15,2,44,73,5,73,26,63,56,86,12,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[55,55,85,50,62,99,84,77,28,85,3,21,27,22,19,26,82,69,54,4,13,7,85,14,1,15,70,59,89,95,10,19,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[4,9,31,92,91,38,92,86,98,75,21,5,64,42,62,84,36,20,73,42,21,23,22,51,51,79,25,45,85,53,3,43,22,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[75,63,2,49,14,12,89,14,60,78,92,16,44,82,38,30,72,11,46,52,90,27,8,65,78,3,85,41,57,79,39,52,33,48,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[78,27,56,56,39,13,19,43,86,72,58,95,39,7,4,34,21,98,39,15,39,84,89,69,84,46,37,57,59,35,59,50,26,15,93,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[42,89,36,27,78,91,24,11,17,41,5,94,7,69,51,96,3,96,47,90,90,45,91,20,50,56,10,32,36,49,4,53,85,92,25,65,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[52,9,61,30,61,97,66,21,96,92,98,90,6,34,96,60,32,69,68,33,75,84,18,31,71,50,84,63,3,3,19,11,28,42,75,45,45,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[61,31,61,68,96,34,49,39,5,71,76,59,62,67,6,47,96,99,34,21,32,47,52,7,71,60,42,72,94,56,82,83,84,40,94,87,82,46,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[1,20,60,14,17,38,26,78,66,81,45,95,18,51,98,81,48,16,53,88,37,52,69,95,72,93,22,34,98,20,54,27,73,61,56,63,60,34,63,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[93,42,94,83,47,61,27,51,79,79,45,1,44,73,31,70,83,42,88,25,53,51,30,15,65,94,80,44,61,84,12,77,2,62,2,65,94,42,14,94,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[32,73,9,67,68,29,74,98,10,19,85,48,38,31,85,67,53,93,93,77,47,67,39,72,94,53,18,43,77,40,78,32,29,59,24,6,2,83,50,60,66,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[32,1,44,30,16,51,15,81,98,15,10,62,86,79,50,62,45,60,70,38,31,85,65,61,64,6,69,84,14,22,56,43,9,48,66,69,83,91,60,40,36,61,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[92,48,22,99,15,95,64,43,1,16,94,2,99,19,17,69,11,58,97,56,89,31,77,45,67,96,12,73,8,20,36,47,81,44,50,64,68,85,40,81,85,52,9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[91,35,92,45,32,84,62,15,19,64,21,66,6,1,52,80,62,59,12,25,88,28,91,50,40,16,22,99,92,79,87,51,21,77,74,77,7,42,38,42,74,83,2,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[46,19,77,66,24,18,5,32,2,84,31,99,92,58,96,72,91,36,62,99,55,29,53,42,12,37,26,58,89,50,66,19,82,75,12,48,24,87,91,85,2,7,3,76,86,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[99,98,84,93,7,17,33,61,92,20,66,60,24,66,40,30,67,5,37,29,24,96,3,27,70,62,13,4,45,47,59,88,43,20,66,15,46,92,30,4,71,66,78,70,53,99,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[67,60,38,6,88,4,17,72,10,99,71,7,42,25,54,5,26,64,91,50,45,71,6,30,67,48,69,82,8,56,80,67,18,46,66,63,1,20,8,80,47,7,91,16,3,79,87,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[18,54,78,49,80,48,77,40,68,23,60,88,58,80,33,57,11,69,55,53,64,2,94,49,60,92,16,35,81,21,82,96,25,24,96,18,2,5,49,3,50,77,6,32,84,27,18,38,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[68,1,50,4,3,21,42,94,53,24,89,5,92,26,52,36,68,11,85,1,4,42,2,45,15,6,50,4,53,73,25,74,81,88,98,21,67,84,79,97,99,20,95,4,40,46,2,58,87,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[94,10,2,78,88,52,21,3,88,60,6,53,49,71,20,91,12,65,7,49,21,22,11,41,58,99,36,16,9,48,17,24,52,36,23,15,72,16,84,56,2,99,43,76,81,71,29,39,49,17,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[64,39,59,84,86,16,17,66,3,9,43,6,64,18,63,29,68,6,23,7,87,14,26,35,17,12,98,41,53,64,78,18,98,27,28,84,80,67,75,62,10,11,76,90,54,10,5,54,41,39,66,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[43,83,18,37,32,31,52,29,95,47,8,76,35,11,4,53,35,43,34,10,52,57,12,36,20,39,40,55,78,44,7,31,38,26,8,15,56,88,86,1,52,62,10,24,32,5,60,65,53,28,57,99,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[3,50,3,52,7,73,49,92,66,80,1,46,8,67,25,36,73,93,7,42,25,53,13,96,76,83,87,90,54,89,78,22,78,91,73,51,69,9,79,94,83,53,9,40,69,62,10,79,49,47,3,81,30,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[71,54,73,33,51,76,59,54,79,37,56,45,84,17,62,21,98,69,41,95,65,24,39,37,62,3,24,48,54,64,46,82,71,78,33,67,9,16,96,68,52,74,79,68,32,21,13,78,96,60,9,69,20,36,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[73,26,21,44,46,38,17,83,65,98,7,23,52,46,61,97,33,13,60,31,70,15,36,77,31,58,56,93,75,68,21,36,69,53,90,75,25,82,39,50,65,94,29,30,11,33,11,13,96,2,56,47,7,49,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[76,46,73,30,10,20,60,70,14,56,34,26,37,39,48,24,55,76,84,91,39,86,95,61,50,14,53,93,64,67,37,31,10,84,42,70,48,20,10,72,60,61,84,79,69,65,99,73,89,25,85,48,92,56,97,16,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[3,14,80,27,22,30,44,27,67,75,79,32,51,54,81,29,65,14,19,4,13,82,4,91,43,40,12,52,29,99,7,76,60,25,1,7,61,71,37,92,40,47,99,66,57,1,43,44,22,40,53,53,9,69,26,81,7,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[49,80,56,90,93,87,47,13,75,28,87,23,72,79,32,18,27,20,28,10,37,59,21,18,70,4,79,96,3,31,45,71,81,6,14,18,17,5,31,50,92,79,23,47,9,39,47,91,43,54,69,47,42,95,62,46,32,85,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[37,18,62,85,87,28,64,5,77,51,47,26,30,65,5,70,65,75,59,80,42,52,25,20,44,10,92,17,71,95,52,14,77,13,24,55,11,65,26,91,1,30,63,15,49,48,41,17,67,47,3,68,20,90,98,32,4,40,68,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[90,51,58,60,6,55,23,68,5,19,76,94,82,36,96,43,38,90,87,28,33,83,5,17,70,83,96,93,6,4,78,47,80,6,23,84,75,23,87,72,99,14,50,98,92,38,90,64,61,58,76,94,36,66,87,80,51,35,61,38,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[57,95,64,6,53,36,82,51,40,33,47,14,7,98,78,65,39,58,53,6,50,53,4,69,40,68,36,69,75,78,75,60,3,32,39,24,74,47,26,90,13,40,44,71,90,76,51,24,36,50,25,45,70,80,61,80,61,43,90,64,11,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[18,29,86,56,68,42,79,10,42,44,30,12,96,18,23,18,52,59,2,99,67,46,60,86,43,38,55,17,44,93,42,21,55,14,47,34,55,16,49,24,23,29,96,51,55,10,46,53,27,92,27,46,63,57,30,65,43,27,21,20,24,83,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[81,72,93,19,69,52,48,1,13,83,92,69,20,48,69,59,20,62,5,42,28,89,90,99,32,72,84,17,8,87,36,3,60,31,36,36,81,26,97,36,48,54,56,56,27,16,91,8,23,11,87,99,33,47,2,14,44,73,70,99,43,35,33,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[90,56,61,86,56,12,70,59,63,32,1,15,81,47,71,76,95,32,65,80,54,70,34,51,40,45,33,4,64,55,78,68,88,47,31,47,68,87,3,84,23,44,89,72,35,8,31,76,63,26,90,85,96,67,65,91,19,14,17,86,4,71,32,95,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[37,13,4,22,64,37,37,28,56,62,86,33,7,37,10,44,52,82,52,6,19,52,57,75,90,26,91,24,6,21,14,67,76,30,46,14,35,89,89,41,3,64,56,97,87,63,22,34,3,79,17,45,11,53,25,56,96,61,23,18,63,31,37,37,47,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[77,23,26,70,72,76,77,4,28,64,71,69,14,85,96,54,95,48,6,62,99,83,86,77,97,75,71,66,30,19,57,90,33,1,60,61,14,12,90,99,32,77,56,41,18,14,87,49,10,14,90,64,18,50,21,74,14,16,88,5,45,73,82,47,74,44,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[22,97,41,13,34,31,54,61,56,94,3,24,59,27,98,77,4,9,37,40,12,26,87,9,71,70,7,18,64,57,80,21,12,71,83,94,60,39,73,79,73,19,97,32,64,29,41,7,48,84,85,67,12,74,95,20,24,52,41,67,56,61,29,93,35,72,69,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[72,23,63,66,1,11,7,30,52,56,95,16,65,26,83,90,50,74,60,18,16,48,43,77,37,11,99,98,30,94,91,26,62,73,45,12,87,73,47,27,1,88,66,99,21,41,95,80,2,53,23,32,61,48,32,43,43,83,14,66,95,91,19,81,80,67,25,88,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[8,62,32,18,92,14,83,71,37,96,11,83,39,99,5,16,23,27,10,67,2,25,44,11,55,31,46,64,41,56,44,74,26,81,51,31,45,85,87,9,81,95,22,28,76,69,46,48,64,87,67,76,27,89,31,11,74,16,62,3,60,94,42,47,9,34,94,93,72,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[56,18,90,18,42,17,42,32,14,86,6,53,33,95,99,35,29,15,44,20,49,59,25,54,34,59,84,21,23,54,35,90,78,16,93,13,37,88,54,19,86,67,68,55,66,84,65,42,98,37,87,56,33,28,58,38,28,38,66,27,52,21,81,15,8,22,97,32,85,27,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[91,53,40,28,13,34,91,25,1,63,50,37,22,49,71,58,32,28,30,18,68,94,23,83,63,62,94,76,80,41,90,22,82,52,29,12,18,56,10,8,35,14,37,57,23,65,67,40,72,39,93,39,70,89,40,34,7,46,94,22,20,5,53,64,56,30,5,56,61,88,27,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[23,95,11,12,37,69,68,24,66,10,87,70,43,50,75,7,62,41,83,58,95,93,89,79,45,39,2,22,5,22,95,43,62,11,68,29,17,40,26,44,25,71,87,16,70,85,19,25,59,94,90,41,41,80,61,70,55,60,84,33,95,76,42,63,15,9,3,40,38,12,3,32,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[9,84,56,80,61,55,85,97,16,94,82,94,98,57,84,30,84,48,93,90,71,5,95,90,73,17,30,98,40,64,65,89,7,79,9,19,56,36,42,30,23,69,73,72,7,5,27,61,24,31,43,48,71,84,21,28,26,65,65,59,65,74,77,20,10,81,61,84,95,8,52,23,70,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[47,81,28,9,98,51,67,64,35,51,59,36,92,82,77,65,80,24,72,53,22,7,27,10,21,28,30,22,48,82,80,48,56,20,14,43,18,25,50,95,90,31,77,8,9,48,44,80,90,22,93,45,82,17,13,96,25,26,8,73,34,99,6,49,24,6,83,51,40,14,15,10,25,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[54,25,10,81,30,64,24,74,75,80,36,75,82,60,22,69,72,91,45,67,3,62,79,54,89,74,44,83,64,96,66,73,44,30,74,50,37,5,9,97,70,1,60,46,37,91,39,75,75,18,58,52,72,78,51,81,86,52,8,97,1,46,43,66,98,62,81,18,70,93,73,8,32,46,34,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[96,80,82,7,59,71,92,53,19,20,88,66,3,26,26,10,24,27,50,82,94,73,63,8,51,33,22,45,19,13,58,33,90,15,22,50,36,13,55,6,35,47,82,52,33,61,36,27,28,46,98,14,73,20,73,32,16,26,80,53,47,66,76,38,94,45,2,1,22,52,47,96,64,58,52,39,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[88,46,23,39,74,63,81,64,20,90,33,33,76,55,58,26,10,46,42,26,74,74,12,83,32,43,9,2,73,55,86,54,85,34,28,23,29,79,91,62,47,41,82,87,99,22,48,90,20,5,96,75,95,4,43,28,81,39,81,1,28,42,78,25,39,77,90,57,58,98,17,36,73,22,63,74,51,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[29,39,74,94,95,78,64,24,38,86,63,87,93,6,70,92,22,16,80,64,29,52,20,27,23,50,14,13,87,15,72,96,81,22,8,49,72,30,70,24,79,31,16,64,59,21,89,34,96,91,48,76,43,53,88,1,57,80,23,81,90,79,58,1,80,87,17,99,86,90,72,63,32,69,14,28,88,69,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[37,17,71,95,56,93,71,35,43,45,4,98,92,94,84,96,11,30,31,27,31,60,92,3,48,5,98,91,86,94,35,90,90,8,48,19,33,28,68,37,59,26,65,96,50,68,22,7,9,49,34,31,77,49,43,6,75,17,81,87,61,79,52,26,27,72,29,50,7,98,86,1,17,10,46,64,24,18,56,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[51,30,25,94,88,85,79,91,40,33,63,84,49,67,98,92,15,26,75,19,82,5,18,78,65,93,61,48,91,43,59,41,70,51,22,15,92,81,67,91,46,98,11,11,65,31,66,10,98,65,83,21,5,56,5,98,73,67,46,74,69,34,8,30,5,52,7,98,32,95,30,94,65,50,24,63,28,81,99,57,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[19,23,61,36,9,89,71,98,65,17,30,29,89,26,79,74,94,11,44,48,97,54,81,55,39,66,69,45,28,47,13,86,15,76,74,70,84,32,36,33,79,20,78,14,41,47,89,28,81,5,99,66,81,86,38,26,6,25,13,60,54,55,23,53,27,5,89,25,23,11,13,54,59,54,56,34,16,24,53,44,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[13,40,57,72,21,15,60,8,4,19,11,98,34,45,9,97,86,71,3,15,56,19,15,44,97,31,90,4,87,87,76,8,12,30,24,62,84,28,12,85,82,53,99,52,13,94,6,65,97,86,9,50,94,68,69,74,30,67,87,94,63,7,78,27,80,36,69,41,6,92,32,78,37,82,30,5,18,87,99,72,19,99,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[44,20,55,77,69,91,27,31,28,81,80,27,2,7,97,23,95,98,12,25,75,29,47,71,7,47,78,39,41,59,27,76,13,15,66,61,68,35,69,86,16,53,67,63,99,85,41,56,8,28,33,40,94,76,90,85,31,70,24,65,84,65,99,82,19,25,54,37,21,46,33,2,52,99,51,33,26,4,87,2,8,18,96,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[54,42,61,45,91,6,64,79,80,82,32,16,83,63,42,49,19,78,65,97,40,42,14,61,49,34,4,18,25,98,59,30,82,72,26,88,54,36,21,75,3,88,99,53,46,51,55,78,22,94,34,40,68,87,84,25,30,76,25,8,92,84,42,61,40,38,9,99,40,23,29,39,46,55,10,90,35,84,56,70,63,23,91,39,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[52,92,3,71,89,7,9,37,68,66,58,20,44,92,51,56,13,71,79,99,26,37,2,6,16,67,36,52,58,16,79,73,56,60,59,27,44,77,94,82,20,50,98,33,9,87,94,37,40,83,64,83,58,85,17,76,53,2,83,52,22,27,39,20,48,92,45,21,9,42,24,23,12,37,52,28,50,78,79,20,86,62,73,20,59,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[54,96,80,15,91,90,99,70,10,9,58,90,93,50,81,99,54,38,36,10,30,11,35,84,16,45,82,18,11,97,36,43,96,79,97,65,40,48,23,19,17,31,64,52,65,65,37,32,65,76,99,79,34,65,79,27,55,33,3,1,33,27,61,28,66,8,4,70,49,46,48,83,1,45,19,96,13,81,14,21,31,79,93,85,50,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[92,92,48,84,59,98,31,53,23,27,15,22,79,95,24,76,5,79,16,93,97,89,38,89,42,83,2,88,94,95,82,21,1,97,48,39,31,78,9,65,50,56,97,61,1,7,65,27,21,23,14,15,80,97,44,78,49,35,33,45,81,74,34,5,31,57,9,38,94,7,69,54,69,32,65,68,46,68,78,90,24,28,49,51,45,86,35,0,0,0,0,0,0,0,0,0,0,0,0,0],[41,63,89,76,87,31,86,9,46,14,87,82,22,29,47,16,13,10,70,72,82,95,48,64,58,43,13,75,42,69,21,12,67,13,64,85,58,23,98,9,37,76,5,22,31,12,66,50,29,99,86,72,45,25,10,28,19,6,90,43,29,31,67,79,46,25,74,14,97,35,76,37,65,46,23,82,6,22,30,76,93,66,94,17,96,13,20,72,0,0,0,0,0,0,0,0,0,0,0,0],[63,40,78,8,52,9,90,41,70,28,36,14,46,44,85,96,24,52,58,15,87,37,5,98,99,39,13,61,76,38,44,99,83,74,90,22,53,80,56,98,30,51,63,39,44,30,91,91,4,22,27,73,17,35,53,18,35,45,54,56,27,78,48,13,69,36,44,38,71,25,30,56,15,22,73,43,32,69,59,25,93,83,45,11,34,94,44,39,92,0,0,0,0,0,0,0,0,0,0,0],[12,36,56,88,13,96,16,12,55,54,11,47,19,78,17,17,68,81,77,51,42,55,99,85,66,27,81,79,93,42,65,61,69,74,14,1,18,56,12,1,58,37,91,22,42,66,83,25,19,4,96,41,25,45,18,69,96,88,36,93,10,12,98,32,44,83,83,4,72,91,4,27,73,7,34,37,71,60,59,31,1,54,54,44,96,93,83,36,4,45,0,0,0,0,0,0,0,0,0,0],[30,18,22,20,42,96,65,79,17,41,55,69,94,81,29,80,91,31,85,25,47,26,43,49,2,99,34,67,99,76,16,14,15,93,8,32,99,44,61,77,67,50,43,55,87,55,53,72,17,46,62,25,50,99,73,5,93,48,17,31,70,80,59,9,44,59,45,13,74,66,58,94,87,73,16,14,85,38,74,99,64,23,79,28,71,42,20,37,82,31,23,0,0,0,0,0,0,0,0,0],[51,96,39,65,46,71,56,13,29,68,53,86,45,33,51,49,12,91,21,21,76,85,2,17,98,15,46,12,60,21,88,30,92,83,44,59,42,50,27,88,46,86,94,73,45,54,23,24,14,10,94,21,20,34,23,51,4,83,99,75,90,63,60,16,22,33,83,70,11,32,10,50,29,30,83,46,11,5,31,17,86,42,49,1,44,63,28,60,7,78,95,40,0,0,0,0,0,0,0,0],[44,61,89,59,4,49,51,27,69,71,46,76,44,4,9,34,56,39,15,6,94,91,75,90,65,27,56,23,74,6,23,33,36,69,14,39,5,34,35,57,33,22,76,46,56,10,61,65,98,9,16,69,4,62,65,18,99,76,49,18,72,66,73,83,82,40,76,31,89,91,27,88,17,35,41,35,32,51,32,67,52,68,74,85,80,57,7,11,62,66,47,22,67,0,0,0,0,0,0,0],[65,37,19,97,26,17,16,24,24,17,50,37,64,82,24,36,32,11,68,34,69,31,32,89,79,93,96,68,49,90,14,23,4,4,67,99,81,74,70,74,36,96,68,9,64,39,88,35,54,89,96,58,66,27,88,97,32,14,6,35,78,20,71,6,85,66,57,2,58,91,72,5,29,56,73,48,86,52,9,93,22,57,79,42,12,1,31,68,17,59,63,76,7,77,0,0,0,0,0,0],[73,81,14,13,17,20,11,9,1,83,8,85,91,70,84,63,62,77,37,7,47,1,59,95,39,69,39,21,99,9,87,2,97,16,92,36,74,71,90,66,33,73,73,75,52,91,11,12,26,53,5,26,26,48,61,50,90,65,1,87,42,47,74,35,22,73,24,26,56,70,52,5,48,41,31,18,83,27,21,39,80,85,26,8,44,2,71,7,63,22,5,52,19,8,20,0,0,0,0,0],[17,25,21,11,72,93,33,49,64,23,53,82,3,13,91,65,85,2,40,5,42,31,77,42,5,36,6,54,4,58,7,76,87,83,25,57,66,12,74,33,85,37,74,32,20,69,3,97,91,68,82,44,19,14,89,28,85,85,80,53,34,87,58,98,88,78,48,65,98,40,11,57,10,67,70,81,60,79,74,72,97,59,79,47,30,20,54,80,89,91,14,5,33,36,79,39,0,0,0,0],[60,85,59,39,60,7,57,76,77,92,6,35,15,72,23,41,45,52,95,18,64,79,86,53,56,31,69,11,91,31,84,50,44,82,22,81,41,40,30,42,30,91,48,94,74,76,64,58,74,25,96,57,14,19,3,99,28,83,15,75,99,1,89,85,79,50,3,95,32,67,44,8,7,41,62,64,29,20,14,76,26,55,48,71,69,66,19,72,44,25,14,1,48,74,12,98,7,0,0,0],[64,66,84,24,18,16,27,48,20,14,47,69,30,86,48,40,23,16,61,21,51,50,26,47,35,33,91,28,78,64,43,68,4,79,51,8,19,60,52,95,6,68,46,86,35,97,27,58,4,65,30,58,99,12,12,75,91,39,50,31,42,64,70,4,46,7,98,73,98,93,37,89,77,91,64,71,64,65,66,21,78,62,81,74,42,20,83,70,73,95,78,45,92,27,34,53,71,15,0,0],[30,11,85,31,34,71,13,48,5,14,44,3,19,67,23,73,19,57,6,90,94,72,57,69,81,62,59,68,88,57,55,69,49,13,7,87,97,80,89,5,71,5,5,26,38,40,16,62,45,99,18,38,98,24,21,26,62,74,69,4,85,57,77,35,58,67,91,79,79,57,86,28,66,34,72,51,76,78,36,95,63,90,8,78,47,63,45,31,22,70,52,48,79,94,15,77,61,67,68,0],[23,33,44,81,80,92,93,75,94,88,23,61,39,76,22,3,28,94,32,6,49,65,41,34,18,23,8,47,62,60,3,63,33,13,80,52,31,54,73,43,70,26,16,69,57,87,83,31,3,93,70,81,47,95,77,44,29,68,39,51,56,59,63,7,25,70,7,77,43,53,64,3,94,42,95,39,18,1,66,21,16,97,20,50,90,16,70,10,95,69,29,6,25,61,41,26,15,59,63,35]];
+```
+
+## --seed-contents--
+
+```js
+function maximumPathSumII(triangle) {
+
+ return true;
+}
+
+const testTriangle = [[3, 0, 0, 0],
+ [7, 4, 0, 0],
+ [2, 4, 6, 0],
+ [8, 5, 9, 3]];
+
+maximumPathSumII(testTriangle);
+```
+
+# --solutions--
+
+```js
+function maximumPathSumII(triangle) {
+ const newTriangle = [];
+ for (let i = 0; i < triangle.length; i++) {
+ newTriangle.push(triangle[i].slice());
+ }
+
+ for (let i = newTriangle.length - 2; i >= 0; i--) {
+ for (let j = i; j >= 0; j--) {
+ let higherOption = 0;
+ if (newTriangle[i + 1][j + 1] > newTriangle[i + 1][j]) {
+ higherOption = newTriangle[i + 1][j + 1];
+ } else {
+ higherOption = newTriangle[i + 1][j];
+ }
+ newTriangle[i][j] += higherOption;
+ }
+ }
+ return newTriangle[0][0];
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-68-magic-5-gon-ring.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-68-magic-5-gon-ring.md
new file mode 100644
index 00000000000..7d8984cc7f8
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-68-magic-5-gon-ring.md
@@ -0,0 +1,71 @@
+---
+id: 5900f3b01000cf542c50fec3
+title: 'Problem 68: Magic 5-gon ring'
+challengeType: 1
+forumTopicId: 302180
+dashedName: problem-68-magic-5-gon-ring
+---
+
+# --description--
+
+Consider the following "magic" 3-gon ring, filled with the numbers 1 to 6, and each line adding to nine.
+
++ 7 4
+ 2 4 6
+ 8 5 9 3 +
+
+Working **clockwise**, and starting from the group of three with the numerically lowest external node (4,3,2 in this example), each solution can be described uniquely. For example, the above solution can be described by the set: 4,3,2; 6,2,1; 5,1,3.
+
+It is possible to complete the ring with four different totals: 9, 10, 11, and 12. There are eight solutions in total.
+
+
+
+|
+
+By concatenating each group it is possible to form 9-digit strings; the maximum string for a 3-gon ring is 432621513.
+
+Using the numbers 1 to 10, and depending on arrangements, it is possible to form 16- and 17-digit strings. What is the maximum **16-digit** string for a "magic" 5-gon ring?
+
+Total
| Solution Set
|
+| -------------------------------------- | --------------------------------------------- |
+| 9 | 4,2,3; 5,3,1; 6,1,2 |
+| 9 | 4,3,2; 6,2,1; 5,1,3 |
+| 10 | 2,3,5; 4,5,1; 6,1,3 |
+| 10 | 2,5,3; 6,3,1; 4,1,5 |
+| 11 | 1,4,6; 3,6,2; 5,2,4 |
+| 11 | 1,6,4; 5,4,2; 3,2,6 |
+| 12 | 1,5,6; 2,6,4; 3,4,5 |
+| 12 | 1,6,5; 3,5,4; 2,4,6 |
+
+
+
+# --hints--
+
+`magic5GonRing()` should return a number.
+
+```js
+assert(typeof magic5GonRing() === 'number');
+```
+
+`magic5GonRing()` should return 6531031914842725.
+
+```js
+assert.strictEqual(magic5GonRing(), 6531031914842725);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function magic5GonRing() {
+
+ return true;
+}
+
+magic5GonRing();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-69-totient-maximum.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-69-totient-maximum.md
new file mode 100644
index 00000000000..e57b133fbe7
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-69-totient-maximum.md
@@ -0,0 +1,110 @@
+---
+id: 5900f3b11000cf542c50fec4
+title: 'Problem 69: Totient maximum'
+challengeType: 1
+forumTopicId: 302181
+dashedName: problem-69-totient-maximum
+---
+
+# --description--
+
+Euler's Totient function, ${\phi}(n)$ (sometimes called the phi function), is used to determine the number of numbers less than `n` which are relatively prime to `n`. For example, as 1, 2, 4, 5, 7, and 8, are all less than nine and relatively prime to nine, ${\phi}(9) = 6$.
+
+
+
+| $n$ | $\text{Relatively Prime}$ | $\displaystyle{\phi}(n)$ | $\displaystyle\frac{n}{{\phi}(n)}$ |
+| --- | ------------------------- | ------------------------ | ---------------------------------- |
+| 2 | 1 | 1 | 2 |
+| 3 | 1,2 | 2 | 1.5 |
+| 4 | 1,3 | 2 | 2 |
+| 5 | 1,2,3,4 | 4 | 1.25 |
+| 6 | 1,5 | 2 | 3 |
+| 7 | 1,2,3,4,5,6 | 6 | 1.1666... |
+| 8 | 1,3,5,7 | 4 | 2 |
+| 9 | 1,2,4,5,7,8 | 6 | 1.5 |
+| 10 | 1,3,7,9 | 4 | 2.5 |
+
+
+
+It can be seen that `n` = 6 produces a maximum $\displaystyle\frac{n}{{\phi}(n)}$ for `n` ≤ 10.
+
+Find the value of `n` ≤ `limit` for which $\displaystyle\frac{n}{{\phi(n)}}$ is a maximum.
+
+# --hints--
+
+`totientMaximum(10)` should return a number.
+
+```js
+assert(typeof totientMaximum(10) === 'number');
+```
+
+`totientMaximum(10)` should return `6`.
+
+```js
+assert.strictEqual(totientMaximum(10), 6);
+```
+
+`totientMaximum(10000)` should return `2310`.
+
+```js
+assert.strictEqual(totientMaximum(10000), 2310);
+```
+
+`totientMaximum(500000)` should return `30030`.
+
+```js
+assert.strictEqual(totientMaximum(500000), 30030);
+```
+
+`totientMaximum(1000000)` should return `510510`.
+
+```js
+assert.strictEqual(totientMaximum(1000000), 510510);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function totientMaximum(limit) {
+
+ return true;
+}
+
+totientMaximum(10);
+```
+
+# --solutions--
+
+```js
+function totientMaximum(limit) {
+ function getSievePrimes(max) {
+ const primesMap = new Array(max).fill(true);
+ primesMap[0] = false;
+ primesMap[1] = false;
+ const primes = [];
+ for (let i = 2; i < max; i = i + 2) {
+ if (primesMap[i]) {
+ primes.push(i);
+ for (let j = i * i; j < max; j = j + i) {
+ primesMap[j] = false;
+ }
+ }
+ if (i === 2) {
+ i = 1;
+ }
+ }
+ return primes;
+ }
+
+ const MAX_PRIME = 50;
+ const primes = getSievePrimes(MAX_PRIME);
+ let result = 1;
+
+ for (let i = 0; result * primes[i] < limit; i++) {
+ result *= primes[i];
+ }
+ return result;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-7-10001st-prime.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-7-10001st-prime.md
new file mode 100644
index 00000000000..6780c8fa2d1
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-7-10001st-prime.md
@@ -0,0 +1,86 @@
+---
+id: 5900f3731000cf542c50fe86
+title: 'Problem 7: 10001st prime'
+challengeType: 1
+forumTopicId: 302182
+dashedName: problem-7-10001st-prime
+---
+
+# --description--
+
+By listing the first six prime numbers: 2, 3, 5, 7, 11, and 13, we can see that the 6th prime is 13.
+
+What is the `n`th prime number?
+
+# --hints--
+
+`nthPrime(6)` should return a number.
+
+```js
+assert(typeof nthPrime(6) === 'number');
+```
+
+`nthPrime(6)` should return 13.
+
+```js
+assert.strictEqual(nthPrime(6), 13);
+```
+
+`nthPrime(10)` should return 29.
+
+```js
+assert.strictEqual(nthPrime(10), 29);
+```
+
+`nthPrime(100)` should return 541.
+
+```js
+assert.strictEqual(nthPrime(100), 541);
+```
+
+`nthPrime(1000)` should return 7919.
+
+```js
+assert.strictEqual(nthPrime(1000), 7919);
+```
+
+`nthPrime(10001)` should return 104743.
+
+```js
+assert.strictEqual(nthPrime(10001), 104743);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function nthPrime(n) {
+
+ return true;
+}
+
+nthPrime(10001);
+```
+
+# --solutions--
+
+```js
+const nthPrime = n => {
+ let pN = 2;
+ let step = 0;
+ while (step < n) {
+ let isPrime = true;
+ let rootN = Math.sqrt(pN);
+ for (let i = 2; i <= rootN; i++) {
+ if (!(pN % i)) {
+ isPrime = false;
+ break;
+ }
+ }
+ isPrime ? step++ : '';
+ pN++;
+ }
+ return pN - 1;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-70-totient-permutation.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-70-totient-permutation.md
new file mode 100644
index 00000000000..1328f1ca1e7
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-70-totient-permutation.md
@@ -0,0 +1,118 @@
+---
+id: 5900f3b21000cf542c50fec5
+title: 'Problem 70: Totient permutation'
+challengeType: 1
+forumTopicId: 302183
+dashedName: problem-70-totient-permutation
+---
+
+# --description--
+
+Euler's Totient function, ${\phi}(n)$ (sometimes called the phi function), is used to determine the number of positive numbers less than or equal to `n` which are relatively prime to `n`. For example, as 1, 2, 4, 5, 7, and 8, are all less than nine and relatively prime to nine, ${\phi}(9) = 6$. The number 1 is considered to be relatively prime to every positive number, so ${\phi}(1) = 1$.
+
+Interestingly, ${\phi}(87109) = 79180$, and it can be seen that 87109 is a permutation of 79180.
+
+Find the value of `n`, 1 < `n` < `limit`, for which ${\phi}(n)$ is a permutation of `n` and the ratio $\displaystyle\frac{n}{{\phi}(n)}$ produces a minimum.
+
+# --hints--
+
+`totientPermutation(10000)` should return a number.
+
+```js
+assert(typeof totientPermutation(10000) === 'number');
+```
+
+`totientPermutation(10000)` should return `4435`.
+
+```js
+assert.strictEqual(totientPermutation(10000), 4435);
+```
+
+`totientPermutation(100000)` should return `75841`.
+
+```js
+assert.strictEqual(totientPermutation(100000), 75841);
+```
+
+`totientPermutation(500000)` should return `474883`.
+
+```js
+assert.strictEqual(totientPermutation(500000), 474883);
+```
+
+`totientPermutation(10000000)` should return `8319823`.
+
+```js
+assert.strictEqual(totientPermutation(10000000), 8319823);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function totientPermutation(limit) {
+
+ return true;
+}
+
+totientPermutation(10000);
+```
+
+# --solutions--
+
+```js
+function totientPermutation(limit) {
+ function getSievePrimes(max) {
+ const primes = [];
+ const primesMap = new Array(max).fill(true);
+ primesMap[0] = false;
+ primesMap[1] = false;
+
+ for (let i = 2; i < max; i += 2) {
+ if (primesMap[i]) {
+ primes.push(i);
+ for (let j = i * i; j < max; j += i) {
+ primesMap[j] = false;
+ }
+ }
+ if (i === 2) {
+ i = 1;
+ }
+ }
+ return primes;
+ }
+
+ function sortDigits(number) {
+ return number.toString().split('').sort().join('');
+ }
+
+ function isPermutation(numberA, numberB) {
+ return sortDigits(numberA) === sortDigits(numberB);
+ }
+
+ const MAX_PRIME = 4000;
+ const primes = getSievePrimes(MAX_PRIME);
+
+ let nValue = 1;
+ let minRatio = Infinity;
+
+ for (let i = 1; i < primes.length; i++) {
+ for (let j = i + 1; j < primes.length; j++) {
+ const num = primes[i] * primes[j];
+ if (num > limit) {
+ break;
+ }
+
+ const phi = (primes[i] - 1) * (primes[j] - 1);
+ const ratio = num / phi;
+
+ if (minRatio > ratio && isPermutation(num, phi)) {
+ nValue = num;
+ minRatio = ratio;
+ }
+ }
+ }
+ return nValue;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-71-ordered-fractions.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-71-ordered-fractions.md
new file mode 100644
index 00000000000..267a17669b0
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-71-ordered-fractions.md
@@ -0,0 +1,95 @@
+---
+id: 5900f3b31000cf542c50fec6
+title: 'Problem 71: Ordered fractions'
+challengeType: 1
+forumTopicId: 302184
+dashedName: problem-71-ordered-fractions
+---
+
+# --description--
+
+Consider the fraction, $\frac{n}{d}$, where `n` and `d` are positive integers. If `n` < `d` and highest common factor, ${{HCF}(n, d)} = 1$, it is called a reduced proper fraction.
+
+If we list the set of reduced proper fractions for `d` ≤ 8 in ascending order of size, we get:
+
+$$\frac{1}{8}, \frac{1}{7}, \frac{1}{6}, \frac{1}{5}, \frac{1}{4}, \frac{2}{7}, \frac{1}{3}, \frac{3}{8}, \frac{\textbf2}{\textbf5}, \frac{3}{7}, \frac{1}{2}, \frac{4}{7}, \frac{3}{5}, \frac{5}{8}, \frac{2}{3}, \frac{5}{7}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \frac{6}{7}, \frac{7}{8}$$
+
+It can be seen that $\frac{2}{5}$ is the fraction immediately to the left of $\frac{3}{7}$.
+
+By listing the set of reduced proper fractions for `d` ≤ `limit` in ascending order of size, find the numerator of the fraction immediately to the left of $\frac{3}{7}$.
+
+# --hints--
+
+`orderedFractions(8)` should return a number.
+
+```js
+assert(typeof orderedFractions(8) === 'number');
+```
+
+`orderedFractions(8)` should return `2`.
+
+```js
+assert.strictEqual(orderedFractions(8), 2);
+```
+
+`orderedFractions(10)` should return `2`.
+
+```js
+assert.strictEqual(orderedFractions(10), 2);
+```
+
+`orderedFractions(9994)` should return `4283`.
+
+```js
+assert.strictEqual(orderedFractions(9994), 4283);
+```
+
+`orderedFractions(500000)` should return `214283`.
+
+```js
+assert.strictEqual(orderedFractions(500000), 214283);
+```
+
+`orderedFractions(1000000)` should return `428570`.
+
+```js
+assert.strictEqual(orderedFractions(1000000), 428570);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function orderedFractions(limit) {
+
+ return true;
+}
+
+orderedFractions(8);
+```
+
+# --solutions--
+
+```js
+function orderedFractions(limit) {
+ const fractions = [];
+ const fractionValues = {};
+ const highBoundary = 3 / 7;
+ let lowBoundary = 2 / 7;
+
+ for (let denominator = limit; denominator > 2; denominator--) {
+ let numerator = Math.floor((3 * denominator - 1) / 7);
+ let value = numerator / denominator;
+ if (value > highBoundary || value < lowBoundary) {
+ continue;
+ }
+ fractionValues[value] = [numerator, denominator];
+ fractions.push(value);
+ lowBoundary = value;
+ }
+
+ fractions.sort();
+ return fractionValues[fractions[fractions.length - 1]][0];
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-72-counting-fractions.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-72-counting-fractions.md
new file mode 100644
index 00000000000..dab392ae0ae
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-72-counting-fractions.md
@@ -0,0 +1,90 @@
+---
+id: 5900f3b41000cf542c50fec7
+title: 'Problem 72: Counting fractions'
+challengeType: 1
+forumTopicId: 302185
+dashedName: problem-72-counting-fractions
+---
+
+# --description--
+
+Consider the fraction, $\frac{n}{d}$, where `n` and `d` are positive integers. If `n` < `d` and highest common factor, ${HCF}(n, d) = 1$, it is called a reduced proper fraction.
+
+If we list the set of reduced proper fractions for `d` ≤ 8 in ascending order of size, we get:
+
+$$\frac{1}{8}, \frac{1}{7}, \frac{1}{6}, \frac{1}{5}, \frac{1}{4}, \frac{2}{7}, \frac{1}{3}, \frac{3}{8}, \frac{2}{5}, \frac{3}{7}, \frac{1}{2}, \frac{4}{7}, \frac{3}{5}, \frac{5}{8}, \frac{2}{3}, \frac{5}{7}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \frac{6}{7}, \frac{7}{8}$$
+
+It can be seen that there are `21` elements in this set.
+
+How many elements would be contained in the set of reduced proper fractions for `d` ≤ `limit`?
+
+# --hints--
+
+`countingFractions(8)` should return a number.
+
+```js
+assert(typeof countingFractions(8) === 'number');
+```
+
+`countingFractions(8)` should return `21`.
+
+```js
+assert.strictEqual(countingFractions(8), 21);
+```
+
+`countingFractions(20000)` should return `121590395`.
+
+```js
+assert.strictEqual(countingFractions(20000), 121590395);
+```
+
+`countingFractions(500000)` should return `75991039675`.
+
+```js
+assert.strictEqual(countingFractions(500000), 75991039675);
+```
+
+`countingFractions(1000000)` should return `303963552391`.
+
+```js
+assert.strictEqual(countingFractions(1000000), 303963552391);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function countingFractions(limit) {
+
+ return true;
+}
+
+countingFractions(8);
+```
+
+# --solutions--
+
+```js
+function countingFractions(limit) {
+ const phi = {};
+ let count = 0;
+
+ for (let i = 2; i <= limit; i++) {
+ if (!phi[i]) {
+ phi[i] = i;
+ }
+ if (phi[i] === i) {
+ for (let j = i; j <= limit; j += i) {
+ if (!phi[j]) {
+ phi[j] = j;
+ }
+ phi[j] = (phi[j] / i) * (i - 1);
+ }
+ }
+ count += phi[i];
+ }
+
+ return count;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-73-counting-fractions-in-a-range.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-73-counting-fractions-in-a-range.md
new file mode 100644
index 00000000000..b53ef258385
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-73-counting-fractions-in-a-range.md
@@ -0,0 +1,83 @@
+---
+id: 5900f3b61000cf542c50fec8
+title: 'Problem 73: Counting fractions in a range'
+challengeType: 1
+forumTopicId: 302186
+dashedName: problem-73-counting-fractions-in-a-range
+---
+
+# --description--
+
+Consider the fraction, $\frac{n}{d}$, where `n` and `d` are positive integers. If `n` < `d` and highest common factor, ${HCF}(n, d) = 1$, it is called a reduced proper fraction.
+
+If we list the set of reduced proper fractions for `d` ≤ 8 in ascending order of size, we get:
+
+$$\frac{1}{8}, \frac{1}{7}, \frac{1}{6}, \frac{1}{5}, \frac{1}{4}, \frac{2}{7}, \frac{1}{3}, \mathbf{\frac{3}{8}, \frac{2}{5}, \frac{3}{7}}, \frac{1}{2}, \frac{4}{7}, \frac{3}{5}, \frac{5}{8}, \frac{2}{3}, \frac{5}{7}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \frac{6}{7}, \frac{7}{8}$$
+
+It can be seen that there are `3` fractions between $\frac{1}{3}$ and $\frac{1}{2}$.
+
+How many fractions lie between $\frac{1}{3}$ and $\frac{1}{2}$ in the sorted set of reduced proper fractions for `d` ≤ `limit`?
+
+# --hints--
+
+`countingFractionsInARange(8)` should return a number.
+
+```js
+assert(typeof countingFractionsInARange(8) === 'number');
+```
+
+`countingFractionsInARange(8)` should return `3`.
+
+```js
+assert.strictEqual(countingFractionsInARange(8), 3);
+```
+
+`countingFractionsInARange(1000)` should return `50695`.
+
+```js
+assert.strictEqual(countingFractionsInARange(1000), 50695);
+```
+
+`countingFractionsInARange(6000)` should return `1823861`.
+
+```js
+assert.strictEqual(countingFractionsInARange(6000), 1823861);
+```
+
+`countingFractionsInARange(12000)` should return `7295372`.
+
+```js
+assert.strictEqual(countingFractionsInARange(12000), 7295372);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function countingFractionsInARange(limit) {
+
+ return true;
+}
+
+countingFractionsInARange(8);
+```
+
+# --solutions--
+
+```js
+function countingFractionsInARange(limit) {
+ let result = 0;
+ const stack = [[3, 2]];
+ while (stack.length > 0) {
+ const [startDenominator, endDenominator] = stack.pop();
+ const curDenominator = startDenominator + endDenominator;
+ if (curDenominator <= limit) {
+ result++;
+ stack.push([startDenominator, curDenominator]);
+ stack.push([curDenominator, endDenominator]);
+ }
+ }
+ return result;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-74-digit-factorial-chains.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-74-digit-factorial-chains.md
new file mode 100644
index 00000000000..0b94dee88dd
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-74-digit-factorial-chains.md
@@ -0,0 +1,127 @@
+---
+id: 5900f3b61000cf542c50fec9
+title: 'Problem 74: Digit factorial chains'
+challengeType: 1
+forumTopicId: 302187
+dashedName: problem-74-digit-factorial-chains
+---
+
+# --description--
+
+The number 145 is well known for the property that the sum of the factorial of its digits is equal to 145:
+
+$$1! + 4! + 5! = 1 + 24 + 120 = 145$$
+
+Perhaps less well known is 169, in that it produces the longest chain of numbers that link back to 169; it turns out that there are only three such loops that exist:
+
+$$\begin{align} &169 → 363601 → 1454 → 169\\\\
+&871 → 45361 → 871\\\\ &872 → 45362 → 872\\\\
+\end{align}$$
+
+It is not difficult to prove that EVERY starting number will eventually get stuck in a loop. For example,
+
+$$\begin{align} &69 → 363600 → 1454 → 169 → 363601\\ (→ 1454)\\\\
+&78 → 45360 → 871 → 45361\\ (→ 871)\\\\ &540 → 145\\ (→ 145)\\\\
+\end{align}$$
+
+Starting with 69 produces a chain of five non-repeating terms, but the longest non-repeating chain with a starting number below one million is sixty terms.
+
+How many chains, with a starting number below `n`, contain exactly sixty non-repeating terms?
+
+# --hints--
+
+`digitFactorialChains(2000)` should return a number.
+
+```js
+assert(typeof digitFactorialChains(2000) === 'number');
+```
+
+`digitFactorialChains(2000)` should return `6`.
+
+```js
+assert.strictEqual(digitFactorialChains(2000), 6);
+```
+
+`digitFactorialChains(100000)` should return `42`.
+
+```js
+assert.strictEqual(digitFactorialChains(100000), 42);
+```
+
+`digitFactorialChains(500000)` should return `282`.
+
+```js
+assert.strictEqual(digitFactorialChains(500000), 282);
+```
+
+`digitFactorialChains(1000000)` should return `402`.
+
+```js
+assert.strictEqual(digitFactorialChains(1000000), 402);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function digitFactorialChains(n) {
+
+ return true;
+}
+
+digitFactorialChains(2000);
+```
+
+# --solutions--
+
+```js
+function digitFactorialChains(n) {
+ function sumDigitsFactorials(number) {
+ let sum = 0;
+ while (number > 0) {
+ sum += factorials[number % 10];
+ number = Math.floor(number / 10);
+ }
+ return sum;
+ }
+
+ const factorials = [1];
+ for (let i = 1; i < 10; i++) {
+ factorials.push(factorials[factorials.length - 1] * i);
+ }
+
+ const sequences = {
+ 169: 3,
+ 871: 2,
+ 872: 2,
+ 1454: 3,
+ 45362: 2,
+ 45461: 2,
+ 3693601: 3
+ };
+ let result = 0;
+
+ for (let i = 2; i < n; i++) {
+ let curNum = i;
+ let chainLength = 0;
+ const curSequence = [];
+ while (curSequence.indexOf(curNum) === -1) {
+ curSequence.push(curNum);
+ curNum = sumDigitsFactorials(curNum);
+ chainLength++;
+ if (sequences.hasOwnProperty(curNum) > 0) {
+ chainLength += sequences[curNum];
+ break;
+ }
+ }
+ if (chainLength === 60) {
+ result++;
+ }
+ for (let j = 1; j < curSequence.length; j++) {
+ sequences[curSequence[j]] = chainLength - j;
+ }
+ }
+ return result;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-75-singular-integer-right-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-75-singular-integer-right-triangles.md
new file mode 100644
index 00000000000..40ab4fb3e00
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-75-singular-integer-right-triangles.md
@@ -0,0 +1,117 @@
+---
+id: 5900f3b71000cf542c50feca
+title: 'Problem 75: Singular integer right triangles'
+challengeType: 1
+forumTopicId: 302188
+dashedName: problem-75-singular-integer-right-triangles
+---
+
+# --description--
+
+It turns out that 12 cm is the smallest length of wire that can be bent to form an integer sided right angle triangle in exactly one way, but there are many more examples.
+
+
+ 12 cm: (3,4,5)
+ 24 cm: (6,8,10)
+ 30 cm: (5,12,13)
+ 36 cm: (9,12,15)
+ 40 cm: (8,15,17)
+ 48 cm: (12,16,20)
+
+
+In contrast, some lengths of wire, like 20 cm, cannot be bent to form an integer sided right angle triangle, and other lengths allow more than one solution to be found; for example, using 120 cm it is possible to form exactly three different integer sided right angle triangles.
+
++ 24 cm: (6,8,10)
+ 30 cm: (5,12,13)
+ 36 cm: (9,12,15)
+ 40 cm: (8,15,17)
+ 48 cm: (12,16,20)
+
+ 120 cm: (30,40,50), (20,48,52), (24,45,51)
+
+
+Given that L is the length of the wire, for how many values of L ≤ `n` can exactly one, integer sided right angle, triangle be formed?
+
+# --hints--
+
+`singularIntRightTriangles(48)` should return a number.
+
+```js
+assert(typeof singularIntRightTriangles(48) === 'number');
+```
+
+`singularIntRightTriangles(48)` should return `6`.
+
+```js
+assert.strictEqual(singularIntRightTriangles(48), 6);
+```
+
+`singularIntRightTriangles(700000)` should return `75783`.
+
+```js
+assert.strictEqual(singularIntRightTriangles(700000), 75783);
+```
+
+`singularIntRightTriangles(1000000)` should return `107876`.
+
+```js
+assert.strictEqual(singularIntRightTriangles(1000000), 107876);
+```
+
+`singularIntRightTriangles(1500000)` should return `161667`.
+
+```js
+assert.strictEqual(singularIntRightTriangles(1500000), 161667);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function singularIntRightTriangles(n) {
+
+ return true;
+}
+
+singularIntRightTriangles(48);
+```
+
+# --solutions--
+
+```js
+function singularIntRightTriangles(limit) {
+ function euclidFormula(m, n) {
+ return [m ** 2 - n ** 2, 2 * m * n, m ** 2 + n ** 2];
+ }
+
+ function gcd(numberA, numberB) {
+ if (numberB === 0) {
+ return numberA;
+ }
+ return gcd(numberB, numberA % numberB);
+ }
+
+ function notBothOdd(numberA, numberB) {
+ return (numberA + numberB) % 2 === 1;
+ }
+
+ function areCoprime(numberA, numberB) {
+ return gcd(numberA, numberB) === 1;
+ }
+
+ const trianglesWithPerimeter = new Array(limit + 1).fill(0);
+ const mLimit = Math.sqrt(limit / 2);
+
+ for (let m = 2; m < mLimit; m++) {
+ for (let n = 1; n < m; n++) {
+ if (notBothOdd(m, n) && areCoprime(m, n)) {
+ const [sideA, sideB, sideC] = euclidFormula(m, n);
+ const perimeter = sideA + sideB + sideC;
+ let curPerimeter = perimeter;
+ while (curPerimeter <= limit) {
+ trianglesWithPerimeter[curPerimeter]++;
+ curPerimeter += perimeter;
+ }
+ }
+ }
+ }
+ return trianglesWithPerimeter.filter(trianglesCount => trianglesCount === 1)
+ .length;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-76-counting-summations.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-76-counting-summations.md
new file mode 100644
index 00000000000..04a358b584d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-76-counting-summations.md
@@ -0,0 +1,83 @@
+---
+id: 5900f3b81000cf542c50fecb
+title: 'Problem 76: Counting summations'
+challengeType: 1
+forumTopicId: 302189
+dashedName: problem-76-counting-summations
+---
+
+# --description--
+
+It is possible to write five as a sum in exactly six different ways:
+
++
+ 4 + 1
+ 3 + 2
+ 3 + 1 + 1
+ 2 + 2 + 1
+ 2 + 1 + 1 + 1
+ 1 + 1 + 1 + 1 + 1
+
+
+How many different ways can `n` be written as a sum of at least two positive integers?
+
+# --hints--
+
+`countingSummations(5)` should return a number.
+
+```js
+assert(typeof countingSummations(5) === 'number');
+```
+
+`countingSummations(5)` should return `6`.
+
+```js
+assert.strictEqual(countingSummations(5), 6);
+```
+
+`countingSummations(20)` should return `626`.
+
+```js
+assert.strictEqual(countingSummations(20), 626);
+```
+
+`countingSummations(50)` should return `204225`.
+
+```js
+assert.strictEqual(countingSummations(50), 204225);
+```
+
+`countingSummations(100)` should return `190569291`.
+
+```js
+assert.strictEqual(countingSummations(100), 190569291);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function countingSummations(n) {
+
+ return true;
+}
+
+countingSummations(5);
+```
+
+# --solutions--
+
+```js
+function countingSummations(n) {
+ const combinations = new Array(n + 1).fill(0);
+ combinations[0] = 1;
+
+ for (let i = 1; i < n; i++) {
+ for (let j = i; j < n + 1; j++) {
+ combinations[j] += combinations[j - i];
+ }
+ }
+ return combinations[n];
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-77-prime-summations.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-77-prime-summations.md
new file mode 100644
index 00000000000..a5639dc73a4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-77-prime-summations.md
@@ -0,0 +1,110 @@
+---
+id: 5900f3b91000cf542c50fecc
+title: 'Problem 77: Prime summations'
+challengeType: 1
+forumTopicId: 302190
+dashedName: problem-77-prime-summations
+---
+
+# --description--
+
+It is possible to write ten as the sum of primes in exactly five different ways:
+
++ 3 + 2
+ 3 + 1 + 1
+ 2 + 2 + 1
+ 2 + 1 + 1 + 1
+ 1 + 1 + 1 + 1 + 1
+
+ 7 + 3
+ 5 + 5
+ 5 + 3 + 2
+ 3 + 3 + 2 + 2
+ 2 + 2 + 2 + 2 + 2
+
+
+What is the first value which can be written as the sum of primes in over `n` ways?
+
+# --hints--
+
+`primeSummations(5)` should return a number.
+
+```js
+assert(typeof primeSummations(5) === 'number');
+```
+
+`primeSummations(5)` should return `11`.
+
+```js
+assert.strictEqual(primeSummations(5), 11);
+```
+
+`primeSummations(100)` should return `31`.
+
+```js
+assert.strictEqual(primeSummations(100), 31);
+```
+
+`primeSummations(1000)` should return `53`.
+
+```js
+assert.strictEqual(primeSummations(1000), 53);
+```
+
+`primeSummations(5000)` should return `71`.
+
+```js
+assert.strictEqual(primeSummations(5000), 71);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeSummations(n) {
+
+ return true;
+}
+
+primeSummations(5);
+```
+
+# --solutions--
+
+```js
+function primeSummations(n) {
+ function getSievePrimes(max) {
+ const primesMap = new Array(max).fill(true);
+ primesMap[0] = false;
+ primesMap[1] = false;
+ const primes = [];
+
+ for (let i = 2; i < max; i += 2) {
+ if (primesMap[i]) {
+ primes.push(i);
+ for (let j = i * i; j < max; j += i) {
+ primesMap[j] = false;
+ }
+ }
+ if (i === 2) {
+ i = 1;
+ }
+ }
+ return primes;
+ }
+
+ const MAX_NUMBER = 100;
+ const primes = getSievePrimes(MAX_NUMBER);
+
+ for (let curNumber = 2; curNumber < MAX_NUMBER; curNumber++) {
+ const combinations = new Array(curNumber + 1).fill(0);
+ combinations[0] = 1;
+ for (let i = 0; i < primes.length; i++) {
+ for (let j = primes[i]; j <= curNumber; j++) {
+ combinations[j] += combinations[j - primes[i]];
+ }
+ }
+ if (combinations[curNumber] > n) {
+ return curNumber;
+ }
+ }
+
+ return false;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-78-coin-partitions.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-78-coin-partitions.md
new file mode 100644
index 00000000000..65d3ebad7e4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-78-coin-partitions.md
@@ -0,0 +1,103 @@
+---
+id: 5900f3ba1000cf542c50fecd
+title: 'Problem 78: Coin partitions'
+challengeType: 1
+forumTopicId: 302191
+dashedName: problem-78-coin-partitions
+---
+
+# --description--
+
+Let ${p}(n)$ represent the number of different ways in which `n` coins can be separated into piles. For example, five coins can be separated into piles in exactly seven different ways, so ${p}(5) = 7$.
+
++ 5 + 5
+ 5 + 3 + 2
+ 3 + 3 + 2 + 2
+ 2 + 2 + 2 + 2 + 2
+
+
+| Coin piles |
+| ----------------- |
+| OOOOO |
+| OOOO O |
+| OOO OO |
+| OOO O O |
+| OO OO O |
+| OO O O O |
+| O O O O O |
+
+
+ +Find the least value of `n` for which ${p}(n)$ is divisible by `divisor`. + +# --hints-- + +`coinPartitions(7)` should return a number. + +```js +assert(typeof coinPartitions(7) === 'number'); +``` + +`coinPartitions(7)` should return `5`. + +```js +assert.strictEqual(coinPartitions(7), 5); +``` + +`coinPartitions(10000)` should return `599`. + +```js +assert.strictEqual(coinPartitions(10000), 599); +``` + +`coinPartitions(100000)` should return `11224`. + +```js +assert.strictEqual(coinPartitions(100000), 11224); +``` + +`coinPartitions(1000000)` should return `55374`. + +```js +assert.strictEqual(coinPartitions(1000000), 55374); +``` + +# --seed-- + +## --seed-contents-- + +```js +function coinPartitions(divisor) { + + return true; +} + +coinPartitions(7); +``` + +# --solutions-- + +```js +function coinPartitions(divisor) { + const partitions = [1]; + + let n = 0; + while (partitions[n] !== 0) { + n++; + partitions.push(0); + + let i = 0; + let pentagonal = 1; + while (pentagonal <= n) { + const sign = i % 4 > 1 ? -1 : 1; + partitions[n] += sign * partitions[n - pentagonal]; + partitions[n] = partitions[n] % divisor; + + i++; + + let k = Math.floor(i / 2) + 1; + if (i % 2 !== 0) { + k *= -1; + } + pentagonal = Math.floor((k * (3 * k - 1)) / 2); + } + } + return n; +} +``` diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-79-passcode-derivation.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-79-passcode-derivation.md new file mode 100644 index 00000000000..a17babe3520 --- /dev/null +++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-79-passcode-derivation.md @@ -0,0 +1,115 @@ +--- +id: 5900f3bb1000cf542c50fece +title: 'Problem 79: Passcode derivation' +challengeType: 1 +forumTopicId: 302192 +dashedName: problem-79-passcode-derivation +--- + +# --description-- + +A common security method used for online banking is to ask the user for three random characters from a passcode. For example, if the passcode was `531278`, they may ask for the 2nd, 3rd, and 5th characters; the expected reply would be: `317`. + +The arrays, `keylog1`, `keylog2`, and `keylog3`, contains fifty successful login attempts. + +Given that the three characters are always asked for in order, analyze the array so as to determine the shortest possible secret passcode of unknown length. + +# --hints-- + +`passcodeDerivation(keylog1)` should return a number. + +```js +assert(typeof passcodeDerivation(_keylog1) === 'number'); +``` + +`passcodeDerivation(keylog1)` should return `531278`. + +```js +assert.strictEqual(passcodeDerivation(_keylog1), 531278); +``` + +`passcodeDerivation(keylog2)` should return `1230567`. + +```js +assert.strictEqual(passcodeDerivation(_keylog2), 1230567); +``` + +`passcodeDerivation(keylog3)` should return `73162890`. + +```js +assert.strictEqual(passcodeDerivation(_keylog3), 73162890); +``` + +# --seed-- + +## --after-user-code-- + +```js +const _keylog1 = [ + 127,327,178,528,537,538,532,328,127,178,537,127,317,328,512,278,328,327,178,327,578,317,527,178,128,328,517,312,531,128,128,317,527,312,328,532,512,518,317,127,537,528,537,527,327,278,532,128, 318,517 +]; +const _keylog2 = [ + 305,367,256,123,357,120,125,307,236,256,356,267,357,256,356,136,257,107,126,567,567,105,120,237,367,120,367,135,207,167,367,367,307,125,120,130,367,230,106,356,126,106,130,123,307,127,306,167,136,126 +]; +const _keylog3 = [ + 319,680,180,690,129,620,762,689,762,318,368,710,720,710,629,168,160,689,716,731,736,729,316,729,729,710,769,290,719,680,318,389,162,289,162,718,729,319,790,680,890,362,319,760,316,729,380,319,728,716, +]; +``` + +## --seed-contents-- + +```js +function passcodeDerivation(arr) { + + return true; +} + +// Only change code above this line + +const keylog1 = [ + 319,680,180,690,129,620,762,689,762,318,368,710,720,710,629,168,160,689,716,731,736,729,316,729,729,710,769,290,719,680,318,389,162,289,162,718,729,319,790,680,890,362,319,760,316,729,380,319,728,716, +]; + +passcodeDerivation(keylog1); +``` + +# --solutions-- + +```js +function passcodeDerivation(arr) { + const numbersInPasscode = []; + const relativePositions = new Array(10) + .fill() + .map(() => new Array(10).fill(0)); + + for (let i = 0; i < arr.length; i++) { + const curAttempt = arr[i] + .toString() + .split('') + .map(key => parseInt(key, 10)); + for (let j = 0; j < curAttempt.length; j++) { + if (numbersInPasscode.indexOf(curAttempt[j]) === -1) { + numbersInPasscode.push(curAttempt[j]); + } + for (let k = j + 1; k < curAttempt.length; k++) { + relativePositions[curAttempt[j]][curAttempt[k]] += 1; + } + } + } + + const ranks = {}; + for (let i = 0; i < numbersInPasscode.length; i++) { + const curNumber = numbersInPasscode[i]; + ranks[curNumber] = relativePositions[curNumber].filter( + count => count > 0 + ).length; + } + + const passcode = numbersInPasscode + .sort((i, j) => ranks[i] - ranks[j]) + .reverse() + .join(''); + + return parseInt(passcode, 10); +} +``` diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-8-largest-product-in-a-series.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-8-largest-product-in-a-series.md new file mode 100644 index 00000000000..c84d410e207 --- /dev/null +++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-8-largest-product-in-a-series.md @@ -0,0 +1,92 @@ +--- +id: 5900f3741000cf542c50fe87 +title: 'Problem 8: Largest product in a series' +challengeType: 1 +forumTopicId: 302193 +dashedName: problem-8-largest-product-in-a-series +--- + +# --description-- + +The four adjacent digits in the 1000-digit number that have the greatest product are 9 × 9 × 8 × 9 = 5832. + +
73167176531330624919225119674426574742355349194934
+96983520312774506326239578318016984801869478851843
+85861560789112949495459501737958331952853208805511
+12540698747158523863050715693290963295227443043557
+66896648950445244523161731856403098711121722383113
+62229893423380308135336276614282806444486645238749
+30358907296290491560440772390713810515859307960866
+70172427121883998797908792274921901699720888093776
+65727333001053367881220235421809751254540594752243
+52584907711670556013604839586446706324415722155397
+53697817977846174064955149290862569321978468622482
+83972241375657056057490261407972968652414535100474
+82166370484403199890008895243450658541227588666881
+16427171479924442928230863465674813919123162824586
+17866458359124566529476545682848912883142607690042
+24219022671055626321111109370544217506941658960408
+07198403850962455444362981230987879927244284909188
+84580156166097919133875499200524063689912560717606
+05886116467109405077541002256983155200055935729725
+71636269561882670428252483600823257530420752963450
+
+Find the `n` adjacent digits in the 1000-digit number that have the greatest product. What is the value of this product?
+
+# --hints--
+
+`largestProductinaSeries(4)` should return a number.
+
+```js
+assert(typeof largestProductinaSeries(4) === 'number');
+```
+
+`largestProductinaSeries(4)` should return 5832.
+
+```js
+assert.strictEqual(largestProductinaSeries(4), 5832);
+```
+
+`largestProductinaSeries(13)` should return 23514624000.
+
+```js
+assert.strictEqual(largestProductinaSeries(13), 23514624000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function largestProductinaSeries(n) {
+
+ let thousandDigits = [7,3,1,6,7,1,7,6,5,3,1,3,3,0,6,2,4,9,1,9,2,2,5,1,1,9,6,7,4,4,2,6,5,7,4,7,4,2,3,5,5,3,4,9,1,9,4,9,3,4,9,6,9,8,3,5,2,0,3,1,2,7,7,4,5,0,6,3,2,6,2,3,9,5,7,8,3,1,8,0,1,6,9,8,4,8,0,1,8,6,9,4,7,8,8,5,1,8,4,3,8,5,8,6,1,5,6,0,7,8,9,1,1,2,9,4,9,4,9,5,4,5,9,5,0,1,7,3,7,9,5,8,3,3,1,9,5,2,8,5,3,2,0,8,8,0,5,5,1,1,1,2,5,4,0,6,9,8,7,4,7,1,5,8,5,2,3,8,6,3,0,5,0,7,1,5,6,9,3,2,9,0,9,6,3,2,9,5,2,2,7,4,4,3,0,4,3,5,5,7,6,6,8,9,6,6,4,8,9,5,0,4,4,5,2,4,4,5,2,3,1,6,1,7,3,1,8,5,6,4,0,3,0,9,8,7,1,1,1,2,1,7,2,2,3,8,3,1,1,3,6,2,2,2,9,8,9,3,4,2,3,3,8,0,3,0,8,1,3,5,3,3,6,2,7,6,6,1,4,2,8,2,8,0,6,4,4,4,4,8,6,6,4,5,2,3,8,7,4,9,3,0,3,5,8,9,0,7,2,9,6,2,9,0,4,9,1,5,6,0,4,4,0,7,7,2,3,9,0,7,1,3,8,1,0,5,1,5,8,5,9,3,0,7,9,6,0,8,6,6,7,0,1,7,2,4,2,7,1,2,1,8,8,3,9,9,8,7,9,7,9,0,8,7,9,2,2,7,4,9,2,1,9,0,1,6,9,9,7,2,0,8,8,8,0,9,3,7,7,6,6,5,7,2,7,3,3,3,0,0,1,0,5,3,3,6,7,8,8,1,2,2,0,2,3,5,4,2,1,8,0,9,7,5,1,2,5,4,5,4,0,5,9,4,7,5,2,2,4,3,5,2,5,8,4,9,0,7,7,1,1,6,7,0,5,5,6,0,1,3,6,0,4,8,3,9,5,8,6,4,4,6,7,0,6,3,2,4,4,1,5,7,2,2,1,5,5,3,9,7,5,3,6,9,7,8,1,7,9,7,7,8,4,6,1,7,4,0,6,4,9,5,5,1,4,9,2,9,0,8,6,2,5,6,9,3,2,1,9,7,8,4,6,8,6,2,2,4,8,2,8,3,9,7,2,2,4,1,3,7,5,6,5,7,0,5,6,0,5,7,4,9,0,2,6,1,4,0,7,9,7,2,9,6,8,6,5,2,4,1,4,5,3,5,1,0,0,4,7,4,8,2,1,6,6,3,7,0,4,8,4,4,0,3,1,9,9,8,9,0,0,0,8,8,9,5,2,4,3,4,5,0,6,5,8,5,4,1,2,2,7,5,8,8,6,6,6,8,8,1,1,6,4,2,7,1,7,1,4,7,9,9,2,4,4,4,2,9,2,8,2,3,0,8,6,3,4,6,5,6,7,4,8,1,3,9,1,9,1,2,3,1,6,2,8,2,4,5,8,6,1,7,8,6,6,4,5,8,3,5,9,1,2,4,5,6,6,5,2,9,4,7,6,5,4,5,6,8,2,8,4,8,9,1,2,8,8,3,1,4,2,6,0,7,6,9,0,0,4,2,2,4,2,1,9,0,2,2,6,7,1,0,5,5,6,2,6,3,2,1,1,1,1,1,0,9,3,7,0,5,4,4,2,1,7,5,0,6,9,4,1,6,5,8,9,6,0,4,0,8,0,7,1,9,8,4,0,3,8,5,0,9,6,2,4,5,5,4,4,4,3,6,2,9,8,1,2,3,0,9,8,7,8,7,9,9,2,7,2,4,4,2,8,4,9,0,9,1,8,8,8,4,5,8,0,1,5,6,1,6,6,0,9,7,9,1,9,1,3,3,8,7,5,4,9,9,2,0,0,5,2,4,0,6,3,6,8,9,9,1,2,5,6,0,7,1,7,6,0,6,0,5,8,8,6,1,1,6,4,6,7,1,0,9,4,0,5,0,7,7,5,4,1,0,0,2,2,5,6,9,8,3,1,5,5,2,0,0,0,5,5,9,3,5,7,2,9,7,2,5,7,1,6,3,6,2,6,9,5,6,1,8,8,2,6,7,0,4,2,8,2,5,2,4,8,3,6,0,0,8,2,3,2,5,7,5,3,0,4,2,0,7,5,2,9,6,3,4,5,0];
+ return true;
+}
+
+largestProductinaSeries(13);
+```
+
+# --solutions--
+
+```js
+const largestProductinaSeries = (number)=>{
+ let thousandDigits = [7,3,1,6,7,1,7,6,5,3,1,3,3,0,6,2,4,9,1,9,2,2,5,1,1,9,6,7,4,4,2,6,5,7,4,7,4,2,3,5,5,3,4,9,1,9,4,9,3,4,9,6,9,8,3,5,2,0,3,1,2,7,7,4,5,0,6,3,2,6,2,3,9,5,7,8,3,1,8,0,1,6,9,8,4,8,0,1,8,6,9,4,7,8,8,5,1,8,4,3,8,5,8,6,1,5,6,0,7,8,9,1,1,2,9,4,9,4,9,5,4,5,9,5,0,1,7,3,7,9,5,8,3,3,1,9,5,2,8,5,3,2,0,8,8,0,5,5,1,1,1,2,5,4,0,6,9,8,7,4,7,1,5,8,5,2,3,8,6,3,0,5,0,7,1,5,6,9,3,2,9,0,9,6,3,2,9,5,2,2,7,4,4,3,0,4,3,5,5,7,6,6,8,9,6,6,4,8,9,5,0,4,4,5,2,4,4,5,2,3,1,6,1,7,3,1,8,5,6,4,0,3,0,9,8,7,1,1,1,2,1,7,2,2,3,8,3,1,1,3,6,2,2,2,9,8,9,3,4,2,3,3,8,0,3,0,8,1,3,5,3,3,6,2,7,6,6,1,4,2,8,2,8,0,6,4,4,4,4,8,6,6,4,5,2,3,8,7,4,9,3,0,3,5,8,9,0,7,2,9,6,2,9,0,4,9,1,5,6,0,4,4,0,7,7,2,3,9,0,7,1,3,8,1,0,5,1,5,8,5,9,3,0,7,9,6,0,8,6,6,7,0,1,7,2,4,2,7,1,2,1,8,8,3,9,9,8,7,9,7,9,0,8,7,9,2,2,7,4,9,2,1,9,0,1,6,9,9,7,2,0,8,8,8,0,9,3,7,7,6,6,5,7,2,7,3,3,3,0,0,1,0,5,3,3,6,7,8,8,1,2,2,0,2,3,5,4,2,1,8,0,9,7,5,1,2,5,4,5,4,0,5,9,4,7,5,2,2,4,3,5,2,5,8,4,9,0,7,7,1,1,6,7,0,5,5,6,0,1,3,6,0,4,8,3,9,5,8,6,4,4,6,7,0,6,3,2,4,4,1,5,7,2,2,1,5,5,3,9,7,5,3,6,9,7,8,1,7,9,7,7,8,4,6,1,7,4,0,6,4,9,5,5,1,4,9,2,9,0,8,6,2,5,6,9,3,2,1,9,7,8,4,6,8,6,2,2,4,8,2,8,3,9,7,2,2,4,1,3,7,5,6,5,7,0,5,6,0,5,7,4,9,0,2,6,1,4,0,7,9,7,2,9,6,8,6,5,2,4,1,4,5,3,5,1,0,0,4,7,4,8,2,1,6,6,3,7,0,4,8,4,4,0,3,1,9,9,8,9,0,0,0,8,8,9,5,2,4,3,4,5,0,6,5,8,5,4,1,2,2,7,5,8,8,6,6,6,8,8,1,1,6,4,2,7,1,7,1,4,7,9,9,2,4,4,4,2,9,2,8,2,3,0,8,6,3,4,6,5,6,7,4,8,1,3,9,1,9,1,2,3,1,6,2,8,2,4,5,8,6,1,7,8,6,6,4,5,8,3,5,9,1,2,4,5,6,6,5,2,9,4,7,6,5,4,5,6,8,2,8,4,8,9,1,2,8,8,3,1,4,2,6,0,7,6,9,0,0,4,2,2,4,2,1,9,0,2,2,6,7,1,0,5,5,6,2,6,3,2,1,1,1,1,1,0,9,3,7,0,5,4,4,2,1,7,5,0,6,9,4,1,6,5,8,9,6,0,4,0,8,0,7,1,9,8,4,0,3,8,5,0,9,6,2,4,5,5,4,4,4,3,6,2,9,8,1,2,3,0,9,8,7,8,7,9,9,2,7,2,4,4,2,8,4,9,0,9,1,8,8,8,4,5,8,0,1,5,6,1,6,6,0,9,7,9,1,9,1,3,3,8,7,5,4,9,9,2,0,0,5,2,4,0,6,3,6,8,9,9,1,2,5,6,0,7,1,7,6,0,6,0,5,8,8,6,1,1,6,4,6,7,1,0,9,4,0,5,0,7,7,5,4,1,0,0,2,2,5,6,9,8,3,1,5,5,2,0,0,0,5,5,9,3,5,7,2,9,7,2,5,7,1,6,3,6,2,6,9,5,6,1,8,8,2,6,7,0,4,2,8,2,5,2,4,8,3,6,0,0,8,2,3,2,5,7,5,3,0,4,2,0,7,5,2,9,6,3,4,5,0];
+ let numberOfDigits = thousandDigits.length;
+ let currentIndex = 0;
+ let productOfAdjDigits = [];
+
+ while(currentIndex<=(numberOfDigits-number)){
+ let currentAdj = thousandDigits.slice(currentIndex,currentIndex+number);
+ let isAdjDigits = false;
+
+ productOfAdjDigits.push(currentAdj.reduce((prev,cur)=>{
+ return prev*cur;
+ }));
+
+ currentIndex++;
+ }
+
+ return Math.max(...productOfAdjDigits);
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-80-square-root-digital-expansion.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-80-square-root-digital-expansion.md
new file mode 100644
index 00000000000..34d7dd6eea4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-80-square-root-digital-expansion.md
@@ -0,0 +1,109 @@
+---
+id: 5900f3bc1000cf542c50fecf
+title: 'Problem 80: Square root digital expansion'
+challengeType: 1
+forumTopicId: 302194
+dashedName: problem-80-square-root-digital-expansion
+---
+
+# --description--
+
+It is well known that if the square root of a natural number is not an integer, then it is irrational. The decimal expansion of such square roots is infinite without any repeating pattern at all.
+
+The square root of two is `1.41421356237309504880...`, and the digital sum of the first one hundred decimal digits is `475`.
+
+For the first `n` natural numbers, find the total of the digital sums of the first one hundred decimal digits for all the irrational square roots.
+
+# --hints--
+
+`sqrtDigitalExpansion(2)` should return a number.
+
+```js
+assert(typeof sqrtDigitalExpansion(2) === 'number');
+```
+
+`sqrtDigitalExpansion(2)` should return `475`.
+
+```js
+assert.strictEqual(sqrtDigitalExpansion(2), 475);
+```
+
+`sqrtDigitalExpansion(50)` should return `19543`.
+
+```js
+assert.strictEqual(sqrtDigitalExpansion(50), 19543);
+```
+
+`sqrtDigitalExpansion(100)` should return `40886`.
+
+```js
+assert.strictEqual(sqrtDigitalExpansion(100), 40886);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sqrtDigitalExpansion(n) {
+
+ return true;
+}
+
+sqrtDigitalExpansion(2);
+```
+
+# --solutions--
+
+```js
+function sqrtDigitalExpansion(n) {
+ function sumDigits(number) {
+ let sum = 0;
+ while (number > 0n) {
+ let digit = number % 10n;
+ sum += parseInt(digit, 10);
+ number = number / 10n;
+ }
+ return sum;
+ }
+
+ function power(numberA, numberB) {
+ let result = 1n;
+ for (let b = 0; b < numberB; b++) {
+ result = result * BigInt(numberA);
+ }
+ return result;
+ }
+
+ // Based on http://www.afjarvis.staff.shef.ac.uk/maths/jarvisspec02.pdf
+ function expandSquareRoot(number, numDigits) {
+ let a = 5n * BigInt(number);
+ let b = 5n;
+ const boundaryWithNeededDigits = power(10, numDigits + 1);
+
+ while (b < boundaryWithNeededDigits) {
+ if (a >= b) {
+ a = a - b;
+ b = b + 10n;
+ } else {
+ a = a * 100n;
+ b = (b / 10n) * 100n + 5n;
+ }
+ }
+ return b / 100n;
+ }
+
+ let result = 0;
+ let nextPerfectRoot = 1;
+ const requiredDigits = 100;
+ for (let i = 1; i <= n; i++) {
+ if (nextPerfectRoot ** 2 === i) {
+ nextPerfectRoot++;
+ continue;
+ }
+ result += sumDigits(expandSquareRoot(i, requiredDigits));
+ }
+
+ return result;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-81-path-sum-two-ways.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-81-path-sum-two-ways.md
new file mode 100644
index 00000000000..5fe3982048f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-81-path-sum-two-ways.md
@@ -0,0 +1,185 @@
+---
+id: 5900f3bd1000cf542c50fed0
+title: 'Problem 81: Path sum: two ways'
+challengeType: 1
+forumTopicId: 302195
+dashedName: problem-81-path-sum-two-ways
+---
+
+# --description--
+
+In the 5 by 5 matrix below, the minimal path sum from the top left to the bottom right, by **only moving to the right and down**, is indicated in bold red and is equal to `2427`.
+
+ $$\begin{pmatrix} \color{red}{131} & 673 & 234 & 103 & 18\\\\
+ \color{red}{201} & \color{red}{96} & \color{red}{342} & 965 & 150\\\\ 630 & 803 & \color{red}{746} & \color{red}{422} & 111\\\\
+ 537 & 699 & 497 & \color{red}{121} & 956\\\\ 805 & 732 & 524 & \color{red}{37} & \color{red}{331} \end{pmatrix}$$
+
+Find the minimal path sum from the top left to the bottom right by only moving right and down in `matrix`, a 2D array representing a matrix. The maximum matrix size used in the tests will be 80 by 80.
+
+# --hints--
+
+`pathSumTwoWays(testMatrix1)` should return a number.
+
+```js
+assert(typeof pathSumTwoWays(_testMatrix1) === 'number');
+```
+
+`pathSumTwoWays(testMatrix1)` should return `2427`.
+
+```js
+assert.strictEqual(pathSumTwoWays(_testMatrix1), 2427);
+```
+
+`pathSumTwoWays(testMatrix2)` should return `427337`.
+
+```js
+assert.strictEqual(pathSumTwoWays(_testMatrix2), 427337);
+```
+
+# --seed--
+
+## --after-user-code--
+
+```js
+const _testMatrix1 = [
+ [131, 673, 234, 103, 18],
+ [201, 96, 342, 965, 150],
+ [630, 803, 746, 422, 111],
+ [537, 699, 497, 121, 956],
+ [805, 732, 524, 37, 331]
+];
+const _testMatrix2 = [
+ [4445,2697,5115,718,2209,2212,654,4348,3079,6821,7668,3276,8874,4190,3785,2752,9473,7817,9137,496,7338,3434,7152,4355,4552,7917,7827,2460,2350,691,3514,5880,3145,7633,7199,3783,5066,7487,3285,1084,8985,760,872,8609,8051,1134,9536,5750,9716,9371,7619,5617,275,9721,2997,2698,1887,8825,6372,3014,2113,7122,7050,6775,5948,2758,1219,3539,348,7989,2735,9862,1263,8089,6401,9462,3168,2758,3748,5870],
+ [1096,20,1318,7586,5167,2642,1443,5741,7621,7030,5526,4244,2348,4641,9827,2448,6918,5883,3737,300,7116,6531,567,5997,3971,6623,820,6148,3287,1874,7981,8424,7672,7575,6797,6717,1078,5008,4051,8795,5820,346,1851,6463,2117,6058,3407,8211,117,4822,1317,4377,4434,5925,8341,4800,1175,4173,690,8978,7470,1295,3799,8724,3509,9849,618,3320,7068,9633,2384,7175,544,6583,1908,9983,481,4187,9353,9377],
+ [9607,7385,521,6084,1364,8983,7623,1585,6935,8551,2574,8267,4781,3834,2764,2084,2669,4656,9343,7709,2203,9328,8004,6192,5856,3555,2260,5118,6504,1839,9227,1259,9451,1388,7909,5733,6968,8519,9973,1663,5315,7571,3035,4325,4283,2304,6438,3815,9213,9806,9536,196,5542,6907,2475,1159,5820,9075,9470,2179,9248,1828,4592,9167,3713,4640,47,3637,309,7344,6955,346,378,9044,8635,7466,5036,9515,6385,9230],
+ [7206,3114,7760,1094,6150,5182,7358,7387,4497,955,101,1478,7777,6966,7010,8417,6453,4955,3496,107,449,8271,131,2948,6185,784,5937,8001,6104,8282,4165,3642,710,2390,575,715,3089,6964,4217,192,5949,7006,715,3328,1152,66,8044,4319,1735,146,4818,5456,6451,4113,1063,4781,6799,602,1504,6245,6550,1417,1343,2363,3785,5448,4545,9371,5420,5068,4613,4882,4241,5043,7873,8042,8434,3939,9256,2187],
+ [3620,8024,577,9997,7377,7682,1314,1158,6282,6310,1896,2509,5436,1732,9480,706,496,101,6232,7375,2207,2306,110,6772,3433,2878,8140,5933,8688,1399,2210,7332,6172,6403,7333,4044,2291,1790,2446,7390,8698,5723,3678,7104,1825,2040,140,3982,4905,4160,2200,5041,2512,1488,2268,1175,7588,8321,8078,7312,977,5257,8465,5068,3453,3096,1651,7906,253,9250,6021,8791,8109,6651,3412,345,4778,5152,4883,7505],
+ [1074,5438,9008,2679,5397,5429,2652,3403,770,9188,4248,2493,4361,8327,9587,707,9525,5913,93,1899,328,2876,3604,673,8576,6908,7659,2544,3359,3883,5273,6587,3065,1749,3223,604,9925,6941,2823,8767,7039,3290,3214,1787,7904,3421,7137,9560,8451,2669,9219,6332,1576,5477,6755,8348,4164,4307,2984,4012,6629,1044,2874,6541,4942,903,1404,9125,5160,8836,4345,2581,460,8438,1538,5507,668,3352,2678,6942],
+ [4295,1176,5596,1521,3061,9868,7037,7129,8933,6659,5947,5063,3653,9447,9245,2679,767,714,116,8558,163,3927,8779,158,5093,2447,5782,3967,1716,931,7772,8164,1117,9244,5783,7776,3846,8862,6014,2330,6947,1777,3112,6008,3491,1906,5952,314,4602,8994,5919,9214,3995,5026,7688,6809,5003,3128,2509,7477,110,8971,3982,8539,2980,4689,6343,5411,2992,5270,5247,9260,2269,7474,1042,7162,5206,1232,4556,4757],
+ [510,3556,5377,1406,5721,4946,2635,7847,4251,8293,8281,6351,4912,287,2870,3380,3948,5322,3840,4738,9563,1906,6298,3234,8959,1562,6297,8835,7861,239,6618,1322,2553,2213,5053,5446,4402,6500,5182,8585,6900,5756,9661,903,5186,7687,5998,7997,8081,8955,4835,6069,2621,1581,732,9564,1082,1853,5442,1342,520,1737,3703,5321,4793,2776,1508,1647,9101,2499,6891,4336,7012,3329,3212,1442,9993,3988,4930,7706],
+ [9444,3401,5891,9716,1228,7107,109,3563,2700,6161,5039,4992,2242,8541,7372,2067,1294,3058,1306,320,8881,5756,9326,411,8650,8824,5495,8282,8397,2000,1228,7817,2099,6473,3571,5994,4447,1299,5991,543,7874,2297,1651,101,2093,3463,9189,6872,6118,872,1008,1779,2805,9084,4048,2123,5877,55,3075,1737,9459,4535,6453,3644,108,5982,4437,5213,1340,6967,9943,5815,669,8074,1838,6979,9132,9315,715,5048],
+ [3327,4030,7177,6336,9933,5296,2621,4785,2755,4832,2512,2118,2244,4407,2170,499,7532,9742,5051,7687,970,6924,3527,4694,5145,1306,2165,5940,2425,8910,3513,1909,6983,346,6377,4304,9330,7203,6605,3709,3346,970,369,9737,5811,4427,9939,3693,8436,5566,1977,3728,2399,3985,8303,2492,5366,9802,9193,7296,1033,5060,9144,2766,1151,7629,5169,5995,58,7619,7565,4208,1713,6279,3209,4908,9224,7409,1325,8540],
+ [6882,1265,1775,3648,4690,959,5837,4520,5394,1378,9485,1360,4018,578,9174,2932,9890,3696,116,1723,1178,9355,7063,1594,1918,8574,7594,7942,1547,6166,7888,354,6932,4651,1010,7759,6905,661,7689,6092,9292,3845,9605,8443,443,8275,5163,7720,7265,6356,7779,1798,1754,5225,6661,1180,8024,5666,88,9153,1840,3508,1193,4445,2648,3538,6243,6375,8107,5902,5423,2520,1122,5015,6113,8859,9370,966,8673,2442],
+ [7338,3423,4723,6533,848,8041,7921,8277,4094,5368,7252,8852,9166,2250,2801,6125,8093,5738,4038,9808,7359,9494,601,9116,4946,2702,5573,2921,9862,1462,1269,2410,4171,2709,7508,6241,7522,615,2407,8200,4189,5492,5649,7353,2590,5203,4274,710,7329,9063,956,8371,3722,4253,4785,1194,4828,4717,4548,940,983,2575,4511,2938,1827,2027,2700,1236,841,5760,1680,6260,2373,3851,1841,4968,1172,5179,7175,3509],
+ [4420,1327,3560,2376,6260,2988,9537,4064,4829,8872,9598,3228,1792,7118,9962,9336,4368,9189,6857,1829,9863,6287,7303,7769,2707,8257,2391,2009,3975,4993,3068,9835,3427,341,8412,2134,4034,8511,6421,3041,9012,2983,7289,100,1355,7904,9186,6920,5856,2008,6545,8331,3655,5011,839,8041,9255,6524,3862,8788,62,7455,3513,5003,8413,3918,2076,7960,6108,3638,6999,3436,1441,4858,4181,1866,8731,7745,3744,1000],
+ [356,8296,8325,1058,1277,4743,3850,2388,6079,6462,2815,5620,8495,5378,75,4324,3441,9870,1113,165,1544,1179,2834,562,6176,2313,6836,8839,2986,9454,5199,6888,1927,5866,8760,320,1792,8296,7898,6121,7241,5886,5814,2815,8336,1576,4314,3109,2572,6011,2086,9061,9403,3947,5487,9731,7281,3159,1819,1334,3181,5844,5114,9898,4634,2531,4412,6430,4262,8482,4546,4555,6804,2607,9421,686,8649,8860,7794,6672],
+ [9870,152,1558,4963,8750,4754,6521,6256,8818,5208,5691,9659,8377,9725,5050,5343,2539,6101,1844,9700,7750,8114,5357,3001,8830,4438,199,9545,8496,43,2078,327,9397,106,6090,8181,8646,6414,7499,5450,4850,6273,5014,4131,7639,3913,6571,8534,9703,4391,7618,445,1320,5,1894,6771,7383,9191,4708,9706,6939,7937,8726,9382,5216,3685,2247,9029,8154,1738,9984,2626,9438,4167,6351,5060,29,1218,1239,4785],
+ [192,5213,8297,8974,4032,6966,5717,1179,6523,4679,9513,1481,3041,5355,9303,9154,1389,8702,6589,7818,6336,3539,5538,3094,6646,6702,6266,2759,4608,4452,617,9406,8064,6379,444,5602,4950,1810,8391,1536,316,8714,1178,5182,5863,5110,5372,4954,1978,2971,5680,4863,2255,4630,5723,2168,538,1692,1319,7540,440,6430,6266,7712,7385,5702,620,641,3136,7350,1478,3155,2820,9109,6261,1122,4470,14,8493,2095],
+ [1046,4301,6082,474,4974,7822,2102,5161,5172,6946,8074,9716,6586,9962,9749,5015,2217,995,5388,4402,7652,6399,6539,1349,8101,3677,1328,9612,7922,2879,231,5887,2655,508,4357,4964,3554,5930,6236,7384,4614,280,3093,9600,2110,7863,2631,6626,6620,68,1311,7198,7561,1768,5139,1431,221,230,2940,968,5283,6517,2146,1646,869,9402,7068,8645,7058,1765,9690,4152,2926,9504,2939,7504,6074,2944,6470,7859],
+ [4659,736,4951,9344,1927,6271,8837,8711,3241,6579,7660,5499,5616,3743,5801,4682,9748,8796,779,1833,4549,8138,4026,775,4170,2432,4174,3741,7540,8017,2833,4027,396,811,2871,1150,9809,2719,9199,8504,1224,540,2051,3519,7982,7367,2761,308,3358,6505,2050,4836,5090,7864,805,2566,2409,6876,3361,8622,5572,5895,3280,441,7893,8105,1634,2929,274,3926,7786,6123,8233,9921,2674,5340,1445,203,4585,3837],
+ [5759,338,7444,7968,7742,3755,1591,4839,1705,650,7061,2461,9230,9391,9373,2413,1213,431,7801,4994,2380,2703,6161,6878,8331,2538,6093,1275,5065,5062,2839,582,1014,8109,3525,1544,1569,8622,7944,2905,6120,1564,1839,5570,7579,1318,2677,5257,4418,5601,7935,7656,5192,1864,5886,6083,5580,6202,8869,1636,7907,4759,9082,5854,3185,7631,6854,5872,5632,5280,1431,2077,9717,7431,4256,8261,9680,4487,4752,4286],
+ [1571,1428,8599,1230,7772,4221,8523,9049,4042,8726,7567,6736,9033,2104,4879,4967,6334,6716,3994,1269,8995,6539,3610,7667,6560,6065,874,848,4597,1711,7161,4811,6734,5723,6356,6026,9183,2586,5636,1092,7779,7923,8747,6887,7505,9909,1792,3233,4526,3176,1508,8043,720,5212,6046,4988,709,5277,8256,3642,1391,5803,1468,2145,3970,6301,7767,2359,8487,9771,8785,7520,856,1605,8972,2402,2386,991,1383,5963],
+ [1822,4824,5957,6511,9868,4113,301,9353,6228,2881,2966,6956,9124,9574,9233,1601,7340,973,9396,540,4747,8590,9535,3650,7333,7583,4806,3593,2738,8157,5215,8472,2284,9473,3906,6982,5505,6053,7936,6074,7179,6688,1564,1103,6860,5839,2022,8490,910,7551,7805,881,7024,1855,9448,4790,1274,3672,2810,774,7623,4223,4850,6071,9975,4935,1915,9771,6690,3846,517,463,7624,4511,614,6394,3661,7409,1395,8127],
+ [8738,3850,9555,3695,4383,2378,87,6256,6740,7682,9546,4255,6105,2000,1851,4073,8957,9022,6547,5189,2487,303,9602,7833,1628,4163,6678,3144,8589,7096,8913,5823,4890,7679,1212,9294,5884,2972,3012,3359,7794,7428,1579,4350,7246,4301,7779,7790,3294,9547,4367,3549,1958,8237,6758,3497,3250,3456,6318,1663,708,7714,6143,6890,3428,6853,9334,7992,591,6449,9786,1412,8500,722,5468,1371,108,3939,4199,2535],
+ [7047,4323,1934,5163,4166,461,3544,2767,6554,203,6098,2265,9078,2075,4644,6641,8412,9183,487,101,7566,5622,1975,5726,2920,5374,7779,5631,3753,3725,2672,3621,4280,1162,5812,345,8173,9785,1525,955,5603,2215,2580,5261,2765,2990,5979,389,3907,2484,1232,5933,5871,3304,1138,1616,5114,9199,5072,7442,7245,6472,4760,6359,9053,7876,2564,9404,3043,9026,2261,3374,4460,7306,2326,966,828,3274,1712,3446],
+ [3975,4565,8131,5800,4570,2306,8838,4392,9147,11,3911,7118,9645,4994,2028,6062,5431,2279,8752,2658,7836,994,7316,5336,7185,3289,1898,9689,2331,5737,3403,1124,2679,3241,7748,16,2724,5441,6640,9368,9081,5618,858,4969,17,2103,6035,8043,7475,2181,939,415,1617,8500,8253,2155,7843,7974,7859,1746,6336,3193,2617,8736,4079,6324,6645,8891,9396,5522,6103,1857,8979,3835,2475,1310,7422,610,8345,7615],
+ [9248,5397,5686,2988,3446,4359,6634,9141,497,9176,6773,7448,1907,8454,916,1596,2241,1626,1384,2741,3649,5362,8791,7170,2903,2475,5325,6451,924,3328,522,90,4813,9737,9557,691,2388,1383,4021,1609,9206,4707,5200,7107,8104,4333,9860,5013,1224,6959,8527,1877,4545,7772,6268,621,4915,9349,5970,706,9583,3071,4127,780,8231,3017,9114,3836,7503,2383,1977,4870,8035,2379,9704,1037,3992,3642,1016,4303],
+ [5093,138,4639,6609,1146,5565,95,7521,9077,2272,974,4388,2465,2650,722,4998,3567,3047,921,2736,7855,173,2065,4238,1048,5,6847,9548,8632,9194,5942,4777,7910,8971,6279,7253,2516,1555,1833,3184,9453,9053,6897,7808,8629,4877,1871,8055,4881,7639,1537,7701,2508,7564,5845,5023,2304,5396,3193,2955,1088,3801,6203,1748,3737,1276,13,4120,7715,8552,3047,2921,106,7508,304,1280,7140,2567,9135,5266],
+ [6237,4607,7527,9047,522,7371,4883,2540,5867,6366,5301,1570,421,276,3361,527,6637,4861,2401,7522,5808,9371,5298,2045,5096,5447,7755,5115,7060,8529,4078,1943,1697,1764,5453,7085,960,2405,739,2100,5800,728,9737,5704,5693,1431,8979,6428,673,7540,6,7773,5857,6823,150,5869,8486,684,5816,9626,7451,5579,8260,3397,5322,6920,1879,2127,2884,5478,4977,9016,6165,6292,3062,5671,5968,78,4619,4763],
+ [9905,7127,9390,5185,6923,3721,9164,9705,4341,1031,1046,5127,7376,6528,3248,4941,1178,7889,3364,4486,5358,9402,9158,8600,1025,874,1839,1783,309,9030,1843,845,8398,1433,7118,70,8071,2877,3904,8866,6722,4299,10,1929,5897,4188,600,1889,3325,2485,6473,4474,7444,6992,4846,6166,4441,2283,2629,4352,7775,1101,2214,9985,215,8270,9750,2740,8361,7103,5930,8664,9690,8302,9267,344,2077,1372,1880,9550],
+ [5825,8517,7769,2405,8204,1060,3603,7025,478,8334,1997,3692,7433,9101,7294,7498,9415,5452,3850,3508,6857,9213,6807,4412,7310,854,5384,686,4978,892,8651,3241,2743,3801,3813,8588,6701,4416,6990,6490,3197,6838,6503,114,8343,5844,8646,8694,65,791,5979,2687,2621,2019,8097,1423,3644,9764,4921,3266,3662,5561,2476,8271,8138,6147,1168,3340,1998,9874,6572,9873,6659,5609,2711,3931,9567,4143,7833,8887],
+ [6223,2099,2700,589,4716,8333,1362,5007,2753,2848,4441,8397,7192,8191,4916,9955,6076,3370,6396,6971,3156,248,3911,2488,4930,2458,7183,5455,170,6809,6417,3390,1956,7188,577,7526,2203,968,8164,479,8699,7915,507,6393,4632,1597,7534,3604,618,3280,6061,9793,9238,8347,568,9645,2070,5198,6482,5000,9212,6655,5961,7513,1323,3872,6170,3812,4146,2736,67,3151,5548,2781,9679,7564,5043,8587,1893,4531],
+ [5826,3690,6724,2121,9308,6986,8106,6659,2142,1642,7170,2877,5757,6494,8026,6571,8387,9961,6043,9758,9607,6450,8631,8334,7359,5256,8523,2225,7487,1977,9555,8048,5763,2414,4948,4265,2427,8978,8088,8841,9208,9601,5810,9398,8866,9138,4176,5875,7212,3272,6759,5678,7649,4922,5422,1343,8197,3154,3600,687,1028,4579,2084,9467,4492,7262,7296,6538,7657,7134,2077,1505,7332,6890,8964,4879,7603,7400,5973,739],
+ [1861,1613,4879,1884,7334,966,2000,7489,2123,4287,1472,3263,4726,9203,1040,4103,6075,6049,330,9253,4062,4268,1635,9960,577,1320,3195,9628,1030,4092,4979,6474,6393,2799,6967,8687,7724,7392,9927,2085,3200,6466,8702,265,7646,8665,7986,7266,4574,6587,612,2724,704,3191,8323,9523,3002,704,5064,3960,8209,2027,2758,8393,4875,4641,9584,6401,7883,7014,768,443,5490,7506,1852,2005,8850,5776,4487,4269],
+ [4052,6687,4705,7260,6645,6715,3706,5504,8672,2853,1136,8187,8203,4016,871,1809,1366,4952,9294,5339,6872,2645,6083,7874,3056,5218,7485,8796,7401,3348,2103,426,8572,4163,9171,3176,948,7654,9344,3217,1650,5580,7971,2622,76,2874,880,2034,9929,1546,2659,5811,3754,7096,7436,9694,9960,7415,2164,953,2360,4194,2397,1047,2196,6827,575,784,2675,8821,6802,7972,5996,6699,2134,7577,2887,1412,4349,4380],
+ [4629,2234,6240,8132,7592,3181,6389,1214,266,1910,2451,8784,2790,1127,6932,1447,8986,2492,5476,397,889,3027,7641,5083,5776,4022,185,3364,5701,2442,2840,4160,9525,4828,6602,2614,7447,3711,4505,7745,8034,6514,4907,2605,7753,6958,7270,6936,3006,8968,439,2326,4652,3085,3425,9863,5049,5361,8688,297,7580,8777,7916,6687,8683,7141,306,9569,2384,1500,3346,4601,7329,9040,6097,2727,6314,4501,4974,2829],
+ [8316,4072,2025,6884,3027,1808,5714,7624,7880,8528,4205,8686,7587,3230,1139,7273,6163,6986,3914,9309,1464,9359,4474,7095,2212,7302,2583,9462,7532,6567,1606,4436,8981,5612,6796,4385,5076,2007,6072,3678,8331,1338,3299,8845,4783,8613,4071,1232,6028,2176,3990,2148,3748,103,9453,538,6745,9110,926,3125,473,5970,8728,7072,9062,1404,1317,5139,9862,6496,6062,3338,464,1600,2532,1088,8232,7739,8274,3873],
+ [2341,523,7096,8397,8301,6541,9844,244,4993,2280,7689,4025,4196,5522,7904,6048,2623,9258,2149,9461,6448,8087,7245,1917,8340,7127,8466,5725,6996,3421,5313,512,9164,9837,9794,8369,4185,1488,7210,1524,1016,4620,9435,2478,7765,8035,697,6677,3724,6988,5853,7662,3895,9593,1185,4727,6025,5734,7665,3070,138,8469,6748,6459,561,7935,8646,2378,462,7755,3115,9690,8877,3946,2728,8793,244,6323,8666,4271],
+ [6430,2406,8994,56,1267,3826,9443,7079,7579,5232,6691,3435,6718,5698,4144,7028,592,2627,217,734,6194,8156,9118,58,2640,8069,4127,3285,694,3197,3377,4143,4802,3324,8134,6953,7625,3598,3584,4289,7065,3434,2106,7132,5802,7920,9060,7531,3321,1725,1067,3751,444,5503,6785,7937,6365,4803,198,6266,8177,1470,6390,1606,2904,7555,9834,8667,2033,1723,5167,1666,8546,8152,473,4475,6451,7947,3062,3281],
+ [2810,3042,7759,1741,2275,2609,7676,8640,4117,1958,7500,8048,1757,3954,9270,1971,4796,2912,660,5511,3553,1012,5757,4525,6084,7198,8352,5775,7726,8591,7710,9589,3122,4392,6856,5016,749,2285,3356,7482,9956,7348,2599,8944,495,3462,3578,551,4543,7207,7169,7796,1247,4278,6916,8176,3742,8385,2310,1345,8692,2667,4568,1770,8319,3585,4920,3890,4928,7343,5385,9772,7947,8786,2056,9266,3454,2807,877,2660],
+ [6206,8252,5928,5837,4177,4333,207,7934,5581,9526,8906,1498,8411,2984,5198,5134,2464,8435,8514,8674,3876,599,5327,826,2152,4084,2433,9327,9697,4800,2728,3608,3849,3861,3498,9943,1407,3991,7191,9110,5666,8434,4704,6545,5944,2357,1163,4995,9619,6754,4200,9682,6654,4862,4744,5953,6632,1054,293,9439,8286,2255,696,8709,1533,1844,6441,430,1999,6063,9431,7018,8057,2920,6266,6799,356,3597,4024,6665],
+ [3847,6356,8541,7225,2325,2946,5199,469,5450,7508,2197,9915,8284,7983,6341,3276,3321,16,1321,7608,5015,3362,8491,6968,6818,797,156,2575,706,9516,5344,5457,9210,5051,8099,1617,9951,7663,8253,9683,2670,1261,4710,1068,8753,4799,1228,2621,3275,6188,4699,1791,9518,8701,5932,4275,6011,9877,2933,4182,6059,2930,6687,6682,9771,654,9437,3169,8596,1827,5471,8909,2352,123,4394,3208,8756,5513,6917,2056],
+ [5458,8173,3138,3290,4570,4892,3317,4251,9699,7973,1163,1935,5477,6648,9614,5655,9592,975,9118,2194,7322,8248,8413,3462,8560,1907,7810,6650,7355,2939,4973,6894,3933,3784,3200,2419,9234,4747,2208,2207,1945,2899,1407,6145,8023,3484,5688,7686,2737,3828,3704,9004,5190,9740,8643,8650,5358,4426,1522,1707,3613,9887,6956,2447,2762,833,1449,9489,2573,1080,4167,3456,6809,2466,227,7125,2759,6250,6472,8089],
+ [3266,7025,9756,3914,1265,9116,7723,9788,6805,5493,2092,8688,6592,9173,4431,4028,6007,7131,4446,4815,3648,6701,759,3312,8355,4485,4187,5188,8746,7759,3528,2177,5243,8379,3838,7233,4607,9187,7216,2190,6967,2920,6082,7910,5354,3609,8958,6949,7731,494,8753,8707,1523,4426,3543,7085,647,6771,9847,646,5049,824,8417,5260,2730,5702,2513,9275,4279,2767,8684,1165,9903,4518,55,9682,8963,6005,2102,6523],
+ [1998,8731,936,1479,5259,7064,4085,91,7745,7136,3773,3810,730,8255,2705,2653,9790,6807,2342,355,9344,2668,3690,2028,9679,8102,574,4318,6481,9175,5423,8062,2867,9657,7553,3442,3920,7430,3945,7639,3714,3392,2525,4995,4850,2867,7951,9667,486,9506,9888,781,8866,1702,3795,90,356,1483,4200,2131,6969,5931,486,6880,4404,1084,5169,4910,6567,8335,4686,5043,2614,3352,2667,4513,6472,7471,5720,1616],
+ [8878,1613,1716,868,1906,2681,564,665,5995,2474,7496,3432,9491,9087,8850,8287,669,823,347,6194,2264,2592,7871,7616,8508,4827,760,2676,4660,4881,7572,3811,9032,939,4384,929,7525,8419,5556,9063,662,8887,7026,8534,3111,1454,2082,7598,5726,6687,9647,7608,73,3014,5063,670,5461,5631,3367,9796,8475,7908,5073,1565,5008,5295,4457,1274,4788,1728,338,600,8415,8535,9351,7750,6887,5845,1741,125],
+ [3637,6489,9634,9464,9055,2413,7824,9517,7532,3577,7050,6186,6980,9365,9782,191,870,2497,8498,2218,2757,5420,6468,586,3320,9230,1034,1393,9886,5072,9391,1178,8464,8042,6869,2075,8275,3601,7715,9470,8786,6475,8373,2159,9237,2066,3264,5000,679,355,3069,4073,494,2308,5512,4334,9438,8786,8637,9774,1169,1949,6594,6072,4270,9158,7916,5752,6794,9391,6301,5842,3285,2141,3898,8027,4310,8821,7079,1307],
+ [8497,6681,4732,7151,7060,5204,9030,7157,833,5014,8723,3207,9796,9286,4913,119,5118,7650,9335,809,3675,2597,5144,3945,5090,8384,187,4102,1260,2445,2792,4422,8389,9290,50,1765,1521,6921,8586,4368,1565,5727,7855,2003,4834,9897,5911,8630,5070,1330,7692,7557,7980,6028,5805,9090,8265,3019,3802,698,9149,5748,1965,9658,4417,5994,5584,8226,2937,272,5743,1278,5698,8736,2595,6475,5342,6596,1149,6920],
+ [8188,8009,9546,6310,8772,2500,9846,6592,6872,3857,1307,8125,7042,1544,6159,2330,643,4604,7899,6848,371,8067,2062,3200,7295,1857,9505,6936,384,2193,2190,301,8535,5503,1462,7380,5114,4824,8833,1763,4974,8711,9262,6698,3999,2645,6937,7747,1128,2933,3556,7943,2885,3122,9105,5447,418,2899,5148,3699,9021,9501,597,4084,175,1621,1,1079,6067,5812,4326,9914,6633,5394,4233,6728,9084,1864,5863,1225],
+ [9935,8793,9117,1825,9542,8246,8437,3331,9128,9675,6086,7075,319,1334,7932,3583,7167,4178,1726,7720,695,8277,7887,6359,5912,1719,2780,8529,1359,2013,4498,8072,1129,9998,1147,8804,9405,6255,1619,2165,7491,1,8882,7378,3337,503,5758,4109,3577,985,3200,7615,8058,5032,1080,6410,6873,5496,1466,2412,9885,5904,4406,3605,8770,4361,6205,9193,1537,9959,214,7260,9566,1685,100,4920,7138,9819,5637,976],
+ [3466,9854,985,1078,7222,8888,5466,5379,3578,4540,6853,8690,3728,6351,7147,3134,6921,9692,857,3307,4998,2172,5783,3931,9417,2541,6299,13,787,2099,9131,9494,896,8600,1643,8419,7248,2660,2609,8579,91,6663,5506,7675,1947,6165,4286,1972,9645,3805,1663,1456,8853,5705,9889,7489,1107,383,4044,2969,3343,152,7805,4980,9929,5033,1737,9953,7197,9158,4071,1324,473,9676,3984,9680,3606,8160,7384,5432],
+ [1005,4512,5186,3953,2164,3372,4097,3247,8697,3022,9896,4101,3871,6791,3219,2742,4630,6967,7829,5991,6134,1197,1414,8923,8787,1394,8852,5019,7768,5147,8004,8825,5062,9625,7988,1110,3992,7984,9966,6516,6251,8270,421,3723,1432,4830,6935,8095,9059,2214,6483,6846,3120,1587,6201,6691,9096,9627,6671,4002,3495,9939,7708,7465,5879,6959,6634,3241,3401,2355,9061,2611,7830,3941,2177,2146,5089,7079,519,6351],
+ [7280,8586,4261,2831,7217,3141,9994,9940,5462,2189,4005,6942,9848,5350,8060,6665,7519,4324,7684,657,9453,9296,2944,6843,7499,7847,1728,9681,3906,6353,5529,2822,3355,3897,7724,4257,7489,8672,4356,3983,1948,6892,7415,4153,5893,4190,621,1736,4045,9532,7701,3671,1211,1622,3176,4524,9317,7800,5638,6644,6943,5463,3531,2821,1347,5958,3436,1438,2999,994,850,4131,2616,1549,3465,5946,690,9273,6954,7991],
+ [9517,399,3249,2596,7736,2142,1322,968,7350,1614,468,3346,3265,7222,6086,1661,5317,2582,7959,4685,2807,2917,1037,5698,1529,3972,8716,2634,3301,3412,8621,743,8001,4734,888,7744,8092,3671,8941,1487,5658,7099,2781,99,1932,4443,4756,4652,9328,1581,7855,4312,5976,7255,6480,3996,2748,1973,9731,4530,2790,9417,7186,5303,3557,351,7182,9428,1342,9020,7599,1392,8304,2070,9138,7215,2008,9937,1106,7110],
+ [7444,769,9688,632,1571,6820,8743,4338,337,3366,3073,1946,8219,104,4210,6986,249,5061,8693,7960,6546,1004,8857,5997,9352,4338,6105,5008,2556,6518,6694,4345,3727,7956,20,3954,8652,4424,9387,2035,8358,5962,5304,5194,8650,8282,1256,1103,2138,6679,1985,3653,2770,2433,4278,615,2863,1715,242,3790,2636,6998,3088,1671,2239,957,5411,4595,6282,2881,9974,2401,875,7574,2987,4587,3147,6766,9885,2965],
+ [3287,3016,3619,6818,9073,6120,5423,557,2900,2015,8111,3873,1314,4189,1846,4399,7041,7583,2427,2864,3525,5002,2069,748,1948,6015,2684,438,770,8367,1663,7887,7759,1885,157,7770,4520,4878,3857,1137,3525,3050,6276,5569,7649,904,4533,7843,2199,5648,7628,9075,9441,3600,7231,2388,5640,9096,958,3058,584,5899,8150,1181,9616,1098,8162,6819,8171,1519,1140,7665,8801,2632,1299,9192,707,9955,2710,7314],
+ [1772,2963,7578,3541,3095,1488,7026,2634,6015,4633,4370,2762,1650,2174,909,8158,2922,8467,4198,4280,9092,8856,8835,5457,2790,8574,9742,5054,9547,4156,7940,8126,9824,7340,8840,6574,3547,1477,3014,6798,7134,435,9484,9859,3031,4,1502,4133,1738,1807,4825,463,6343,9701,8506,9822,9555,8688,8168,3467,3234,6318,1787,5591,419,6593,7974,8486,9861,6381,6758,194,3061,4315,2863,4665,3789,2201,1492,4416],
+ [126,8927,6608,5682,8986,6867,1715,6076,3159,788,3140,4744,830,9253,5812,5021,7616,8534,1546,9590,1101,9012,9821,8132,7857,4086,1069,7491,2988,1579,2442,4321,2149,7642,6108,250,6086,3167,24,9528,7663,2685,1220,9196,1397,5776,1577,1730,5481,977,6115,199,6326,2183,3767,5928,5586,7561,663,8649,9688,949,5913,9160,1870,5764,9887,4477,6703,1413,4995,5494,7131,2192,8969,7138,3997,8697,646,1028],
+ [8074,1731,8245,624,4601,8706,155,8891,309,2552,8208,8452,2954,3124,3469,4246,3352,1105,4509,8677,9901,4416,8191,9283,5625,7120,2952,8881,7693,830,4580,8228,9459,8611,4499,1179,4988,1394,550,2336,6089,6872,269,7213,1848,917,6672,4890,656,1478,6536,3165,4743,4990,1176,6211,7207,5284,9730,4738,1549,4986,4942,8645,3698,9429,1439,2175,6549,3058,6513,1574,6988,8333,3406,5245,5431,7140,7085,6407],
+ [7845,4694,2530,8249,290,5948,5509,1588,5940,4495,5866,5021,4626,3979,3296,7589,4854,1998,5627,3926,8346,6512,9608,1918,7070,4747,4182,2858,2766,4606,6269,4107,8982,8568,9053,4244,5604,102,2756,727,5887,2566,7922,44,5986,621,1202,374,6988,4130,3627,6744,9443,4568,1398,8679,397,3928,9159,367,2917,6127,5788,3304,8129,911,2669,1463,9749,264,4478,8940,1109,7309,2462,117,4692,7724,225,2312],
+ [4164,3637,2000,941,8903,39,3443,7172,1031,3687,4901,8082,4945,4515,7204,9310,9349,9535,9940,218,1788,9245,2237,1541,5670,6538,6047,5553,9807,8101,1925,8714,445,8332,7309,6830,5786,5736,7306,2710,3034,1838,7969,6318,7912,2584,2080,7437,6705,2254,7428,820,782,9861,7596,3842,3631,8063,5240,6666,394,4565,7865,4895,9890,6028,6117,4724,9156,4473,4552,602,470,6191,4927,5387,884,3146,1978,3000],
+ [4258,6880,1696,3582,5793,4923,2119,1155,9056,9698,6603,3768,5514,9927,9609,6166,6566,4536,4985,4934,8076,9062,6741,6163,7399,4562,2337,5600,2919,9012,8459,1308,6072,1225,9306,8818,5886,7243,7365,8792,6007,9256,6699,7171,4230,7002,8720,7839,4533,1671,478,7774,1607,2317,5437,4705,7886,4760,6760,7271,3081,2997,3088,7675,6208,3101,6821,6840,122,9633,4900,2067,8546,4549,2091,7188,5605,8599,6758,5229],
+ [7854,5243,9155,3556,8812,7047,2202,1541,5993,4600,4760,713,434,7911,7426,7414,8729,322,803,7960,7563,4908,6285,6291,736,3389,9339,4132,8701,7534,5287,3646,592,3065,7582,2592,8755,6068,8597,1982,5782,1894,2900,6236,4039,6569,3037,5837,7698,700,7815,2491,7272,5878,3083,6778,6639,3589,5010,8313,2581,6617,5869,8402,6808,2951,2321,5195,497,2190,6187,1342,1316,4453,7740,4154,2959,1781,1482,8256],
+ [7178,2046,4419,744,8312,5356,6855,8839,319,2962,5662,47,6307,8662,68,4813,567,2712,9931,1678,3101,8227,6533,4933,6656,92,5846,4780,6256,6361,4323,9985,1231,2175,7178,3034,9744,6155,9165,7787,5836,9318,7860,9644,8941,6480,9443,8188,5928,161,6979,2352,5628,6991,1198,8067,5867,6620,3778,8426,2994,3122,3124,6335,3918,8897,2655,9670,634,1088,1576,8935,7255,474,8166,7417,9547,2886,5560,3842],
+ [6957,3111,26,7530,7143,1295,1744,6057,3009,1854,8098,5405,2234,4874,9447,2620,9303,27,7410,969,40,2966,5648,7596,8637,4238,3143,3679,7187,690,9980,7085,7714,9373,5632,7526,6707,3951,9734,4216,2146,3602,5371,6029,3039,4433,4855,4151,1449,3376,8009,7240,7027,4602,2947,9081,4045,8424,9352,8742,923,2705,4266,3232,2264,6761,363,2651,3383,7770,6730,7856,7340,9679,2158,610,4471,4608,910,6241],
+ [4417,6756,1013,8797,658,8809,5032,8703,7541,846,3357,2920,9817,1745,9980,7593,4667,3087,779,3218,6233,5568,4296,2289,2654,7898,5021,9461,5593,8214,9173,4203,2271,7980,2983,5952,9992,8399,3468,1776,3188,9314,1720,6523,2933,621,8685,5483,8986,6163,3444,9539,4320,155,3992,2828,2150,6071,524,2895,5468,8063,1210,3348,9071,4862,483,9017,4097,6186,9815,3610,5048,1644,1003,9865,9332,2145,1944,2213],
+ [9284,3803,4920,1927,6706,4344,7383,4786,9890,2010,5228,1224,3158,6967,8580,8990,8883,5213,76,8306,2031,4980,5639,9519,7184,5645,7769,3259,8077,9130,1317,3096,9624,3818,1770,695,2454,947,6029,3474,9938,3527,5696,4760,7724,7738,2848,6442,5767,6845,8323,4131,2859,7595,2500,4815,3660,9130,8580,7016,8231,4391,8369,3444,4069,4021,556,6154,627,2778,1496,4206,6356,8434,8491,3816,8231,3190,5575,1015],
+ [3787,7572,1788,6803,5641,6844,1961,4811,8535,9914,9999,1450,8857,738,4662,8569,6679,2225,7839,8618,286,2648,5342,2294,3205,4546,176,8705,3741,6134,8324,8021,7004,5205,7032,6637,9442,5539,5584,4819,5874,5807,8589,6871,9016,983,1758,3786,1519,6241,185,8398,495,3370,9133,3051,4549,9674,7311,9738,3316,9383,2658,2776,9481,7558,619,3943,3324,6491,4933,153,9738,4623,912,3595,7771,7939,1219,4405],
+ [2650,3883,4154,5809,315,7756,4430,1788,4451,1631,6461,7230,6017,5751,138,588,5282,2442,9110,9035,6349,2515,1570,6122,4192,4174,3530,1933,4186,4420,4609,5739,4135,2963,6308,1161,8809,8619,2796,3819,6971,8228,4188,1492,909,8048,2328,6772,8467,7671,9068,2226,7579,6422,7056,8042,3296,2272,3006,2196,7320,3238,3490,3102,37,1293,3212,4767,5041,8773,5794,4456,6174,7279,7054,2835,7053,9088,790,6640],
+ [3101,1057,7057,3826,6077,1025,2955,1224,1114,6729,5902,4698,6239,7203,9423,1804,4417,6686,1426,6941,8071,1029,4985,9010,6122,6597,1622,1574,3513,1684,7086,5505,3244,411,9638,4150,907,9135,829,981,1707,5359,8781,9751,5,9131,3973,7159,1340,6955,7514,7993,6964,8198,1933,2797,877,3993,4453,8020,9349,8646,2779,8679,2961,3547,3374,3510,1129,3568,2241,2625,9138,5974,8206,7669,7678,1833,8700,4480],
+ [4865,9912,8038,8238,782,3095,8199,1127,4501,7280,2112,2487,3626,2790,9432,1475,6312,8277,4827,2218,5806,7132,8752,1468,7471,6386,739,8762,8323,8120,5169,9078,9058,3370,9560,7987,8585,8531,5347,9312,1058,4271,1159,5286,5404,6925,8606,9204,7361,2415,560,586,4002,2644,1927,2824,768,4409,2942,3345,1002,808,4941,6267,7979,5140,8643,7553,9438,7320,4938,2666,4609,2778,8158,6730,3748,3867,1866,7181],
+ [171,3771,7134,8927,4778,2913,3326,2004,3089,7853,1378,1729,4777,2706,9578,1360,5693,3036,1851,7248,2403,2273,8536,6501,9216,613,9671,7131,7719,6425,773,717,8803,160,1114,7554,7197,753,4513,4322,8499,4533,2609,4226,8710,6627,644,9666,6260,4870,5744,7385,6542,6203,7703,6130,8944,5589,2262,6803,6381,7414,6888,5123,7320,9392,9061,6780,322,8975,7050,5089,1061,2260,3199,1150,1865,5386,9699,6501],
+ [3744,8454,6885,8277,919,1923,4001,6864,7854,5519,2491,6057,8794,9645,1776,5714,9786,9281,7538,6916,3215,395,2501,9618,4835,8846,9708,2813,3303,1794,8309,7176,2206,1602,1838,236,4593,2245,8993,4017,10,8215,6921,5206,4023,5932,6997,7801,262,7640,3107,8275,4938,7822,2425,3223,3886,2105,8700,9526,2088,8662,8034,7004,5710,2124,7164,3574,6630,9980,4242,2901,9471,1491,2117,4562,1130,9086,4117,6698],
+ [2810,2280,2331,1170,4554,4071,8387,1215,2274,9848,6738,1604,7281,8805,439,1298,8318,7834,9426,8603,6092,7944,1309,8828,303,3157,4638,4439,9175,1921,4695,7716,1494,1015,1772,5913,1127,1952,1950,8905,4064,9890,385,9357,7945,5035,7082,5369,4093,6546,5187,5637,2041,8946,1758,7111,6566,1027,1049,5148,7224,7248,296,6169,375,1656,7993,2816,3717,4279,4675,1609,3317,42,6201,3100,3144,163,9530,4531],
+ [7096,6070,1009,4988,3538,5801,7149,3063,2324,2912,7911,7002,4338,7880,2481,7368,3516,2016,7556,2193,1388,3865,8125,4637,4096,8114,750,3144,1938,7002,9343,4095,1392,4220,3455,6969,9647,1321,9048,1996,1640,6626,1788,314,9578,6630,2813,6626,4981,9908,7024,4355,3201,3521,3864,3303,464,1923,595,9801,3391,8366,8084,9374,1041,8807,9085,1892,9431,8317,9016,9221,8574,9981,9240,5395,2009,6310,2854,9255],
+ [8830,3145,2960,9615,8220,6061,3452,2918,6481,9278,2297,3385,6565,7066,7316,5682,107,7646,4466,68,1952,9603,8615,54,7191,791,6833,2560,693,9733,4168,570,9127,9537,1925,8287,5508,4297,8452,8795,6213,7994,2420,4208,524,5915,8602,8330,2651,8547,6156,1812,6271,7991,9407,9804,1553,6866,1128,2119,4691,9711,8315,5879,9935,6900,482,682,4126,1041,428,6247,3720,5882,7526,2582,4327,7725,3503,2631],
+ [2738,9323,721,7434,1453,6294,2957,3786,5722,6019,8685,4386,3066,9057,6860,499,5315,3045,5194,7111,3137,9104,941,586,3066,755,4177,8819,7040,5309,3583,3897,4428,7788,4721,7249,6559,7324,825,7311,3760,6064,6070,9672,4882,584,1365,9739,9331,5783,2624,7889,1604,1303,1555,7125,8312,425,8936,3233,7724,1480,403,7440,1784,1754,4721,1569,652,3893,4574,5692,9730,4813,9844,8291,9199,7101,3391,8914],
+ [6044,2928,9332,3328,8588,447,3830,1176,3523,2705,8365,6136,5442,9049,5526,8575,8869,9031,7280,706,2794,8814,5767,4241,7696,78,6570,556,5083,1426,4502,3336,9518,2292,1885,3740,3153,9348,9331,8051,2759,5407,9028,7840,9255,831,515,2612,9747,7435,8964,4971,2048,4900,5967,8271,1719,9670,2810,6777,1594,6367,6259,8316,3815,1689,6840,9437,4361,822,9619,3065,83,6344,7486,8657,8228,9635,6932,4864],
+ [8478,4777,6334,4678,7476,4963,6735,3096,5860,1405,5127,7269,7793,4738,227,9168,2996,8928,765,733,1276,7677,6258,1528,9558,3329,302,8901,1422,8277,6340,645,9125,8869,5952,141,8141,1816,9635,4025,4184,3093,83,2344,2747,9352,7966,1206,1126,1826,218,7939,2957,2729,810,8752,5247,4174,4038,8884,7899,9567,301,5265,5752,7524,4381,1669,3106,8270,6228,6373,754,2547,4240,2313,5514,3022,1040,9738],
+ [2265,8192,1763,1369,8469,8789,4836,52,1212,6690,5257,8918,6723,6319,378,4039,2421,8555,8184,9577,1432,7139,8078,5452,9628,7579,4161,7490,5159,8559,1011,81,478,5840,1964,1334,6875,8670,9900,739,1514,8692,522,9316,6955,1345,8132,2277,3193,9773,3923,4177,2183,1236,6747,6575,4874,6003,6409,8187,745,8776,9440,7543,9825,2582,7381,8147,7236,5185,7564,6125,218,7991,6394,391,7659,7456,5128,5294],
+ [2132,8992,8160,5782,4420,3371,3798,5054,552,5631,7546,4716,1332,6486,7892,7441,4370,6231,4579,2121,8615,1145,9391,1524,1385,2400,9437,2454,7896,7467,2928,8400,3299,4025,7458,4703,7206,6358,792,6200,725,4275,4136,7390,5984,4502,7929,5085,8176,4600,119,3568,76,9363,6943,2248,9077,9731,6213,5817,6729,4190,3092,6910,759,2682,8380,1254,9604,3011,9291,5329,9453,9746,2739,6522,3765,5634,1113,5789],
+ [5304,5499,564,2801,679,2653,1783,3608,7359,7797,3284,796,3222,437,7185,6135,8571,2778,7488,5746,678,6140,861,7750,803,9859,9918,2425,3734,2698,9005,4864,9818,6743,2475,132,9486,3825,5472,919,292,4411,7213,7699,6435,9019,6769,1388,802,2124,1345,8493,9487,8558,7061,8777,8833,2427,2238,5409,4957,8503,3171,7622,5779,6145,2417,5873,5563,5693,9574,9491,1937,7384,4563,6842,5432,2751,3406,7981]
+];
+```
+
+## --seed-contents--
+
+```js
+function pathSumTwoWays(matrix) {
+
+ return true;
+}
+
+// Only change code above this line
+
+const testMatrix1 = [
+ [131, 673, 234, 103, 18],
+ [201, 96, 342, 965, 150],
+ [630, 803, 746, 422, 111],
+ [537, 699, 497, 121, 956],
+ [805, 732, 524, 37, 331]
+];
+
+pathSumTwoWays(testMatrix1);
+```
+
+# --solutions--
+
+```js
+function pathSumTwoWays(matrix) {
+ function makeMinimalMove(row, column) {
+ if (resultMatrix[row][column + 1] < resultMatrix[row + 1][column]) {
+ return resultMatrix[row][column + 1];
+ }
+ return resultMatrix[row + 1][column];
+ }
+
+ const size = matrix.length;
+ const resultMatrix = [];
+ for (let i = 0; i < size; i++) {
+ resultMatrix.push([...matrix[i]])
+ }
+
+ for (let i = size - 2; i >= 0; i--) {
+ resultMatrix[size - 1][i] += resultMatrix[size - 1][i + 1];
+ resultMatrix[i][size - 1] += resultMatrix[i + 1][size - 1];
+ }
+
+ for (let row = size - 2; row >= 0; row--) {
+ for (let column = size - 2; column >= 0; column--) {
+ resultMatrix[row][column] += makeMinimalMove(row, column);
+ }
+ }
+ return resultMatrix[0][0];
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-82-path-sum-three-ways.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-82-path-sum-three-ways.md
new file mode 100644
index 00000000000..0895540d468
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-82-path-sum-three-ways.md
@@ -0,0 +1,195 @@
+---
+id: 5900f3be1000cf542c50fed1
+title: 'Problem 82: Path sum: three ways'
+challengeType: 1
+forumTopicId: 302196
+dashedName: problem-82-path-sum-three-ways
+---
+
+# --description--
+
+**Note:** This problem is a more challenging version of Problem 81.
+
+The minimal path sum in the 5 by 5 matrix below, by starting in any cell in the left column and finishing in any cell in the right column, and only moving up, down, and right, is indicated in red and bold; the sum is equal to `994`.
+
+ $$\begin{pmatrix} 131 & 673 & \color{red}{234} & \color{red}{103} & \color{red}{18}\\\\
+ \color{red}{201} & \color{red}{96} & \color{red}{342} & 965 & 150\\\\ 630 & 803 & 746 & 422 & 111\\\\
+ 537 & 699 & 497 & 121 & 956\\\\ 805 & 732 & 524 & 37 & 331 \end{pmatrix}$$
+
+Find the minimal path sum from the left column to the right column in `matrix`, a 2D array representing a matrix. The maximum matrix size used in tests will be 80 by 80.
+
+# --hints--
+
+`pathSumThreeWays(testMatrix1)` should return a number.
+
+```js
+assert(typeof pathSumThreeWays(_testMatrix1) === 'number');
+```
+
+`pathSumThreeWays(testMatrix1)` should return `994`.
+
+```js
+assert.strictEqual(pathSumThreeWays(_testMatrix1), 994);
+```
+
+`pathSumThreeWays(testMatrix2)` should return `260324`.
+
+```js
+assert.strictEqual(pathSumThreeWays(_testMatrix2), 260324);
+```
+
+# --seed--
+
+## --after-user-code--
+
+```js
+const _testMatrix1 = [
+ [131, 673, 234, 103, 18],
+ [201, 96, 342, 965, 150],
+ [630, 803, 746, 422, 111],
+ [537, 699, 497, 121, 956],
+ [805, 732, 524, 37, 331]
+];
+const _testMatrix2 = [
+ [4445,2697,5115,718,2209,2212,654,4348,3079,6821,7668,3276,8874,4190,3785,2752,9473,7817,9137,496,7338,3434,7152,4355,4552,7917,7827,2460,2350,691,3514,5880,3145,7633,7199,3783,5066,7487,3285,1084,8985,760,872,8609,8051,1134,9536,5750,9716,9371,7619,5617,275,9721,2997,2698,1887,8825,6372,3014,2113,7122,7050,6775,5948,2758,1219,3539,348,7989,2735,9862,1263,8089,6401,9462,3168,2758,3748,5870],
+ [1096,20,1318,7586,5167,2642,1443,5741,7621,7030,5526,4244,2348,4641,9827,2448,6918,5883,3737,300,7116,6531,567,5997,3971,6623,820,6148,3287,1874,7981,8424,7672,7575,6797,6717,1078,5008,4051,8795,5820,346,1851,6463,2117,6058,3407,8211,117,4822,1317,4377,4434,5925,8341,4800,1175,4173,690,8978,7470,1295,3799,8724,3509,9849,618,3320,7068,9633,2384,7175,544,6583,1908,9983,481,4187,9353,9377],
+ [9607,7385,521,6084,1364,8983,7623,1585,6935,8551,2574,8267,4781,3834,2764,2084,2669,4656,9343,7709,2203,9328,8004,6192,5856,3555,2260,5118,6504,1839,9227,1259,9451,1388,7909,5733,6968,8519,9973,1663,5315,7571,3035,4325,4283,2304,6438,3815,9213,9806,9536,196,5542,6907,2475,1159,5820,9075,9470,2179,9248,1828,4592,9167,3713,4640,47,3637,309,7344,6955,346,378,9044,8635,7466,5036,9515,6385,9230],
+ [7206,3114,7760,1094,6150,5182,7358,7387,4497,955,101,1478,7777,6966,7010,8417,6453,4955,3496,107,449,8271,131,2948,6185,784,5937,8001,6104,8282,4165,3642,710,2390,575,715,3089,6964,4217,192,5949,7006,715,3328,1152,66,8044,4319,1735,146,4818,5456,6451,4113,1063,4781,6799,602,1504,6245,6550,1417,1343,2363,3785,5448,4545,9371,5420,5068,4613,4882,4241,5043,7873,8042,8434,3939,9256,2187],
+ [3620,8024,577,9997,7377,7682,1314,1158,6282,6310,1896,2509,5436,1732,9480,706,496,101,6232,7375,2207,2306,110,6772,3433,2878,8140,5933,8688,1399,2210,7332,6172,6403,7333,4044,2291,1790,2446,7390,8698,5723,3678,7104,1825,2040,140,3982,4905,4160,2200,5041,2512,1488,2268,1175,7588,8321,8078,7312,977,5257,8465,5068,3453,3096,1651,7906,253,9250,6021,8791,8109,6651,3412,345,4778,5152,4883,7505],
+ [1074,5438,9008,2679,5397,5429,2652,3403,770,9188,4248,2493,4361,8327,9587,707,9525,5913,93,1899,328,2876,3604,673,8576,6908,7659,2544,3359,3883,5273,6587,3065,1749,3223,604,9925,6941,2823,8767,7039,3290,3214,1787,7904,3421,7137,9560,8451,2669,9219,6332,1576,5477,6755,8348,4164,4307,2984,4012,6629,1044,2874,6541,4942,903,1404,9125,5160,8836,4345,2581,460,8438,1538,5507,668,3352,2678,6942],
+ [4295,1176,5596,1521,3061,9868,7037,7129,8933,6659,5947,5063,3653,9447,9245,2679,767,714,116,8558,163,3927,8779,158,5093,2447,5782,3967,1716,931,7772,8164,1117,9244,5783,7776,3846,8862,6014,2330,6947,1777,3112,6008,3491,1906,5952,314,4602,8994,5919,9214,3995,5026,7688,6809,5003,3128,2509,7477,110,8971,3982,8539,2980,4689,6343,5411,2992,5270,5247,9260,2269,7474,1042,7162,5206,1232,4556,4757],
+ [510,3556,5377,1406,5721,4946,2635,7847,4251,8293,8281,6351,4912,287,2870,3380,3948,5322,3840,4738,9563,1906,6298,3234,8959,1562,6297,8835,7861,239,6618,1322,2553,2213,5053,5446,4402,6500,5182,8585,6900,5756,9661,903,5186,7687,5998,7997,8081,8955,4835,6069,2621,1581,732,9564,1082,1853,5442,1342,520,1737,3703,5321,4793,2776,1508,1647,9101,2499,6891,4336,7012,3329,3212,1442,9993,3988,4930,7706],
+ [9444,3401,5891,9716,1228,7107,109,3563,2700,6161,5039,4992,2242,8541,7372,2067,1294,3058,1306,320,8881,5756,9326,411,8650,8824,5495,8282,8397,2000,1228,7817,2099,6473,3571,5994,4447,1299,5991,543,7874,2297,1651,101,2093,3463,9189,6872,6118,872,1008,1779,2805,9084,4048,2123,5877,55,3075,1737,9459,4535,6453,3644,108,5982,4437,5213,1340,6967,9943,5815,669,8074,1838,6979,9132,9315,715,5048],
+ [3327,4030,7177,6336,9933,5296,2621,4785,2755,4832,2512,2118,2244,4407,2170,499,7532,9742,5051,7687,970,6924,3527,4694,5145,1306,2165,5940,2425,8910,3513,1909,6983,346,6377,4304,9330,7203,6605,3709,3346,970,369,9737,5811,4427,9939,3693,8436,5566,1977,3728,2399,3985,8303,2492,5366,9802,9193,7296,1033,5060,9144,2766,1151,7629,5169,5995,58,7619,7565,4208,1713,6279,3209,4908,9224,7409,1325,8540],
+ [6882,1265,1775,3648,4690,959,5837,4520,5394,1378,9485,1360,4018,578,9174,2932,9890,3696,116,1723,1178,9355,7063,1594,1918,8574,7594,7942,1547,6166,7888,354,6932,4651,1010,7759,6905,661,7689,6092,9292,3845,9605,8443,443,8275,5163,7720,7265,6356,7779,1798,1754,5225,6661,1180,8024,5666,88,9153,1840,3508,1193,4445,2648,3538,6243,6375,8107,5902,5423,2520,1122,5015,6113,8859,9370,966,8673,2442],
+ [7338,3423,4723,6533,848,8041,7921,8277,4094,5368,7252,8852,9166,2250,2801,6125,8093,5738,4038,9808,7359,9494,601,9116,4946,2702,5573,2921,9862,1462,1269,2410,4171,2709,7508,6241,7522,615,2407,8200,4189,5492,5649,7353,2590,5203,4274,710,7329,9063,956,8371,3722,4253,4785,1194,4828,4717,4548,940,983,2575,4511,2938,1827,2027,2700,1236,841,5760,1680,6260,2373,3851,1841,4968,1172,5179,7175,3509],
+ [4420,1327,3560,2376,6260,2988,9537,4064,4829,8872,9598,3228,1792,7118,9962,9336,4368,9189,6857,1829,9863,6287,7303,7769,2707,8257,2391,2009,3975,4993,3068,9835,3427,341,8412,2134,4034,8511,6421,3041,9012,2983,7289,100,1355,7904,9186,6920,5856,2008,6545,8331,3655,5011,839,8041,9255,6524,3862,8788,62,7455,3513,5003,8413,3918,2076,7960,6108,3638,6999,3436,1441,4858,4181,1866,8731,7745,3744,1000],
+ [356,8296,8325,1058,1277,4743,3850,2388,6079,6462,2815,5620,8495,5378,75,4324,3441,9870,1113,165,1544,1179,2834,562,6176,2313,6836,8839,2986,9454,5199,6888,1927,5866,8760,320,1792,8296,7898,6121,7241,5886,5814,2815,8336,1576,4314,3109,2572,6011,2086,9061,9403,3947,5487,9731,7281,3159,1819,1334,3181,5844,5114,9898,4634,2531,4412,6430,4262,8482,4546,4555,6804,2607,9421,686,8649,8860,7794,6672],
+ [9870,152,1558,4963,8750,4754,6521,6256,8818,5208,5691,9659,8377,9725,5050,5343,2539,6101,1844,9700,7750,8114,5357,3001,8830,4438,199,9545,8496,43,2078,327,9397,106,6090,8181,8646,6414,7499,5450,4850,6273,5014,4131,7639,3913,6571,8534,9703,4391,7618,445,1320,5,1894,6771,7383,9191,4708,9706,6939,7937,8726,9382,5216,3685,2247,9029,8154,1738,9984,2626,9438,4167,6351,5060,29,1218,1239,4785],
+ [192,5213,8297,8974,4032,6966,5717,1179,6523,4679,9513,1481,3041,5355,9303,9154,1389,8702,6589,7818,6336,3539,5538,3094,6646,6702,6266,2759,4608,4452,617,9406,8064,6379,444,5602,4950,1810,8391,1536,316,8714,1178,5182,5863,5110,5372,4954,1978,2971,5680,4863,2255,4630,5723,2168,538,1692,1319,7540,440,6430,6266,7712,7385,5702,620,641,3136,7350,1478,3155,2820,9109,6261,1122,4470,14,8493,2095],
+ [1046,4301,6082,474,4974,7822,2102,5161,5172,6946,8074,9716,6586,9962,9749,5015,2217,995,5388,4402,7652,6399,6539,1349,8101,3677,1328,9612,7922,2879,231,5887,2655,508,4357,4964,3554,5930,6236,7384,4614,280,3093,9600,2110,7863,2631,6626,6620,68,1311,7198,7561,1768,5139,1431,221,230,2940,968,5283,6517,2146,1646,869,9402,7068,8645,7058,1765,9690,4152,2926,9504,2939,7504,6074,2944,6470,7859],
+ [4659,736,4951,9344,1927,6271,8837,8711,3241,6579,7660,5499,5616,3743,5801,4682,9748,8796,779,1833,4549,8138,4026,775,4170,2432,4174,3741,7540,8017,2833,4027,396,811,2871,1150,9809,2719,9199,8504,1224,540,2051,3519,7982,7367,2761,308,3358,6505,2050,4836,5090,7864,805,2566,2409,6876,3361,8622,5572,5895,3280,441,7893,8105,1634,2929,274,3926,7786,6123,8233,9921,2674,5340,1445,203,4585,3837],
+ [5759,338,7444,7968,7742,3755,1591,4839,1705,650,7061,2461,9230,9391,9373,2413,1213,431,7801,4994,2380,2703,6161,6878,8331,2538,6093,1275,5065,5062,2839,582,1014,8109,3525,1544,1569,8622,7944,2905,6120,1564,1839,5570,7579,1318,2677,5257,4418,5601,7935,7656,5192,1864,5886,6083,5580,6202,8869,1636,7907,4759,9082,5854,3185,7631,6854,5872,5632,5280,1431,2077,9717,7431,4256,8261,9680,4487,4752,4286],
+ [1571,1428,8599,1230,7772,4221,8523,9049,4042,8726,7567,6736,9033,2104,4879,4967,6334,6716,3994,1269,8995,6539,3610,7667,6560,6065,874,848,4597,1711,7161,4811,6734,5723,6356,6026,9183,2586,5636,1092,7779,7923,8747,6887,7505,9909,1792,3233,4526,3176,1508,8043,720,5212,6046,4988,709,5277,8256,3642,1391,5803,1468,2145,3970,6301,7767,2359,8487,9771,8785,7520,856,1605,8972,2402,2386,991,1383,5963],
+ [1822,4824,5957,6511,9868,4113,301,9353,6228,2881,2966,6956,9124,9574,9233,1601,7340,973,9396,540,4747,8590,9535,3650,7333,7583,4806,3593,2738,8157,5215,8472,2284,9473,3906,6982,5505,6053,7936,6074,7179,6688,1564,1103,6860,5839,2022,8490,910,7551,7805,881,7024,1855,9448,4790,1274,3672,2810,774,7623,4223,4850,6071,9975,4935,1915,9771,6690,3846,517,463,7624,4511,614,6394,3661,7409,1395,8127],
+ [8738,3850,9555,3695,4383,2378,87,6256,6740,7682,9546,4255,6105,2000,1851,4073,8957,9022,6547,5189,2487,303,9602,7833,1628,4163,6678,3144,8589,7096,8913,5823,4890,7679,1212,9294,5884,2972,3012,3359,7794,7428,1579,4350,7246,4301,7779,7790,3294,9547,4367,3549,1958,8237,6758,3497,3250,3456,6318,1663,708,7714,6143,6890,3428,6853,9334,7992,591,6449,9786,1412,8500,722,5468,1371,108,3939,4199,2535],
+ [7047,4323,1934,5163,4166,461,3544,2767,6554,203,6098,2265,9078,2075,4644,6641,8412,9183,487,101,7566,5622,1975,5726,2920,5374,7779,5631,3753,3725,2672,3621,4280,1162,5812,345,8173,9785,1525,955,5603,2215,2580,5261,2765,2990,5979,389,3907,2484,1232,5933,5871,3304,1138,1616,5114,9199,5072,7442,7245,6472,4760,6359,9053,7876,2564,9404,3043,9026,2261,3374,4460,7306,2326,966,828,3274,1712,3446],
+ [3975,4565,8131,5800,4570,2306,8838,4392,9147,11,3911,7118,9645,4994,2028,6062,5431,2279,8752,2658,7836,994,7316,5336,7185,3289,1898,9689,2331,5737,3403,1124,2679,3241,7748,16,2724,5441,6640,9368,9081,5618,858,4969,17,2103,6035,8043,7475,2181,939,415,1617,8500,8253,2155,7843,7974,7859,1746,6336,3193,2617,8736,4079,6324,6645,8891,9396,5522,6103,1857,8979,3835,2475,1310,7422,610,8345,7615],
+ [9248,5397,5686,2988,3446,4359,6634,9141,497,9176,6773,7448,1907,8454,916,1596,2241,1626,1384,2741,3649,5362,8791,7170,2903,2475,5325,6451,924,3328,522,90,4813,9737,9557,691,2388,1383,4021,1609,9206,4707,5200,7107,8104,4333,9860,5013,1224,6959,8527,1877,4545,7772,6268,621,4915,9349,5970,706,9583,3071,4127,780,8231,3017,9114,3836,7503,2383,1977,4870,8035,2379,9704,1037,3992,3642,1016,4303],
+ [5093,138,4639,6609,1146,5565,95,7521,9077,2272,974,4388,2465,2650,722,4998,3567,3047,921,2736,7855,173,2065,4238,1048,5,6847,9548,8632,9194,5942,4777,7910,8971,6279,7253,2516,1555,1833,3184,9453,9053,6897,7808,8629,4877,1871,8055,4881,7639,1537,7701,2508,7564,5845,5023,2304,5396,3193,2955,1088,3801,6203,1748,3737,1276,13,4120,7715,8552,3047,2921,106,7508,304,1280,7140,2567,9135,5266],
+ [6237,4607,7527,9047,522,7371,4883,2540,5867,6366,5301,1570,421,276,3361,527,6637,4861,2401,7522,5808,9371,5298,2045,5096,5447,7755,5115,7060,8529,4078,1943,1697,1764,5453,7085,960,2405,739,2100,5800,728,9737,5704,5693,1431,8979,6428,673,7540,6,7773,5857,6823,150,5869,8486,684,5816,9626,7451,5579,8260,3397,5322,6920,1879,2127,2884,5478,4977,9016,6165,6292,3062,5671,5968,78,4619,4763],
+ [9905,7127,9390,5185,6923,3721,9164,9705,4341,1031,1046,5127,7376,6528,3248,4941,1178,7889,3364,4486,5358,9402,9158,8600,1025,874,1839,1783,309,9030,1843,845,8398,1433,7118,70,8071,2877,3904,8866,6722,4299,10,1929,5897,4188,600,1889,3325,2485,6473,4474,7444,6992,4846,6166,4441,2283,2629,4352,7775,1101,2214,9985,215,8270,9750,2740,8361,7103,5930,8664,9690,8302,9267,344,2077,1372,1880,9550],
+ [5825,8517,7769,2405,8204,1060,3603,7025,478,8334,1997,3692,7433,9101,7294,7498,9415,5452,3850,3508,6857,9213,6807,4412,7310,854,5384,686,4978,892,8651,3241,2743,3801,3813,8588,6701,4416,6990,6490,3197,6838,6503,114,8343,5844,8646,8694,65,791,5979,2687,2621,2019,8097,1423,3644,9764,4921,3266,3662,5561,2476,8271,8138,6147,1168,3340,1998,9874,6572,9873,6659,5609,2711,3931,9567,4143,7833,8887],
+ [6223,2099,2700,589,4716,8333,1362,5007,2753,2848,4441,8397,7192,8191,4916,9955,6076,3370,6396,6971,3156,248,3911,2488,4930,2458,7183,5455,170,6809,6417,3390,1956,7188,577,7526,2203,968,8164,479,8699,7915,507,6393,4632,1597,7534,3604,618,3280,6061,9793,9238,8347,568,9645,2070,5198,6482,5000,9212,6655,5961,7513,1323,3872,6170,3812,4146,2736,67,3151,5548,2781,9679,7564,5043,8587,1893,4531],
+ [5826,3690,6724,2121,9308,6986,8106,6659,2142,1642,7170,2877,5757,6494,8026,6571,8387,9961,6043,9758,9607,6450,8631,8334,7359,5256,8523,2225,7487,1977,9555,8048,5763,2414,4948,4265,2427,8978,8088,8841,9208,9601,5810,9398,8866,9138,4176,5875,7212,3272,6759,5678,7649,4922,5422,1343,8197,3154,3600,687,1028,4579,2084,9467,4492,7262,7296,6538,7657,7134,2077,1505,7332,6890,8964,4879,7603,7400,5973,739],
+ [1861,1613,4879,1884,7334,966,2000,7489,2123,4287,1472,3263,4726,9203,1040,4103,6075,6049,330,9253,4062,4268,1635,9960,577,1320,3195,9628,1030,4092,4979,6474,6393,2799,6967,8687,7724,7392,9927,2085,3200,6466,8702,265,7646,8665,7986,7266,4574,6587,612,2724,704,3191,8323,9523,3002,704,5064,3960,8209,2027,2758,8393,4875,4641,9584,6401,7883,7014,768,443,5490,7506,1852,2005,8850,5776,4487,4269],
+ [4052,6687,4705,7260,6645,6715,3706,5504,8672,2853,1136,8187,8203,4016,871,1809,1366,4952,9294,5339,6872,2645,6083,7874,3056,5218,7485,8796,7401,3348,2103,426,8572,4163,9171,3176,948,7654,9344,3217,1650,5580,7971,2622,76,2874,880,2034,9929,1546,2659,5811,3754,7096,7436,9694,9960,7415,2164,953,2360,4194,2397,1047,2196,6827,575,784,2675,8821,6802,7972,5996,6699,2134,7577,2887,1412,4349,4380],
+ [4629,2234,6240,8132,7592,3181,6389,1214,266,1910,2451,8784,2790,1127,6932,1447,8986,2492,5476,397,889,3027,7641,5083,5776,4022,185,3364,5701,2442,2840,4160,9525,4828,6602,2614,7447,3711,4505,7745,8034,6514,4907,2605,7753,6958,7270,6936,3006,8968,439,2326,4652,3085,3425,9863,5049,5361,8688,297,7580,8777,7916,6687,8683,7141,306,9569,2384,1500,3346,4601,7329,9040,6097,2727,6314,4501,4974,2829],
+ [8316,4072,2025,6884,3027,1808,5714,7624,7880,8528,4205,8686,7587,3230,1139,7273,6163,6986,3914,9309,1464,9359,4474,7095,2212,7302,2583,9462,7532,6567,1606,4436,8981,5612,6796,4385,5076,2007,6072,3678,8331,1338,3299,8845,4783,8613,4071,1232,6028,2176,3990,2148,3748,103,9453,538,6745,9110,926,3125,473,5970,8728,7072,9062,1404,1317,5139,9862,6496,6062,3338,464,1600,2532,1088,8232,7739,8274,3873],
+ [2341,523,7096,8397,8301,6541,9844,244,4993,2280,7689,4025,4196,5522,7904,6048,2623,9258,2149,9461,6448,8087,7245,1917,8340,7127,8466,5725,6996,3421,5313,512,9164,9837,9794,8369,4185,1488,7210,1524,1016,4620,9435,2478,7765,8035,697,6677,3724,6988,5853,7662,3895,9593,1185,4727,6025,5734,7665,3070,138,8469,6748,6459,561,7935,8646,2378,462,7755,3115,9690,8877,3946,2728,8793,244,6323,8666,4271],
+ [6430,2406,8994,56,1267,3826,9443,7079,7579,5232,6691,3435,6718,5698,4144,7028,592,2627,217,734,6194,8156,9118,58,2640,8069,4127,3285,694,3197,3377,4143,4802,3324,8134,6953,7625,3598,3584,4289,7065,3434,2106,7132,5802,7920,9060,7531,3321,1725,1067,3751,444,5503,6785,7937,6365,4803,198,6266,8177,1470,6390,1606,2904,7555,9834,8667,2033,1723,5167,1666,8546,8152,473,4475,6451,7947,3062,3281],
+ [2810,3042,7759,1741,2275,2609,7676,8640,4117,1958,7500,8048,1757,3954,9270,1971,4796,2912,660,5511,3553,1012,5757,4525,6084,7198,8352,5775,7726,8591,7710,9589,3122,4392,6856,5016,749,2285,3356,7482,9956,7348,2599,8944,495,3462,3578,551,4543,7207,7169,7796,1247,4278,6916,8176,3742,8385,2310,1345,8692,2667,4568,1770,8319,3585,4920,3890,4928,7343,5385,9772,7947,8786,2056,9266,3454,2807,877,2660],
+ [6206,8252,5928,5837,4177,4333,207,7934,5581,9526,8906,1498,8411,2984,5198,5134,2464,8435,8514,8674,3876,599,5327,826,2152,4084,2433,9327,9697,4800,2728,3608,3849,3861,3498,9943,1407,3991,7191,9110,5666,8434,4704,6545,5944,2357,1163,4995,9619,6754,4200,9682,6654,4862,4744,5953,6632,1054,293,9439,8286,2255,696,8709,1533,1844,6441,430,1999,6063,9431,7018,8057,2920,6266,6799,356,3597,4024,6665],
+ [3847,6356,8541,7225,2325,2946,5199,469,5450,7508,2197,9915,8284,7983,6341,3276,3321,16,1321,7608,5015,3362,8491,6968,6818,797,156,2575,706,9516,5344,5457,9210,5051,8099,1617,9951,7663,8253,9683,2670,1261,4710,1068,8753,4799,1228,2621,3275,6188,4699,1791,9518,8701,5932,4275,6011,9877,2933,4182,6059,2930,6687,6682,9771,654,9437,3169,8596,1827,5471,8909,2352,123,4394,3208,8756,5513,6917,2056],
+ [5458,8173,3138,3290,4570,4892,3317,4251,9699,7973,1163,1935,5477,6648,9614,5655,9592,975,9118,2194,7322,8248,8413,3462,8560,1907,7810,6650,7355,2939,4973,6894,3933,3784,3200,2419,9234,4747,2208,2207,1945,2899,1407,6145,8023,3484,5688,7686,2737,3828,3704,9004,5190,9740,8643,8650,5358,4426,1522,1707,3613,9887,6956,2447,2762,833,1449,9489,2573,1080,4167,3456,6809,2466,227,7125,2759,6250,6472,8089],
+ [3266,7025,9756,3914,1265,9116,7723,9788,6805,5493,2092,8688,6592,9173,4431,4028,6007,7131,4446,4815,3648,6701,759,3312,8355,4485,4187,5188,8746,7759,3528,2177,5243,8379,3838,7233,4607,9187,7216,2190,6967,2920,6082,7910,5354,3609,8958,6949,7731,494,8753,8707,1523,4426,3543,7085,647,6771,9847,646,5049,824,8417,5260,2730,5702,2513,9275,4279,2767,8684,1165,9903,4518,55,9682,8963,6005,2102,6523],
+ [1998,8731,936,1479,5259,7064,4085,91,7745,7136,3773,3810,730,8255,2705,2653,9790,6807,2342,355,9344,2668,3690,2028,9679,8102,574,4318,6481,9175,5423,8062,2867,9657,7553,3442,3920,7430,3945,7639,3714,3392,2525,4995,4850,2867,7951,9667,486,9506,9888,781,8866,1702,3795,90,356,1483,4200,2131,6969,5931,486,6880,4404,1084,5169,4910,6567,8335,4686,5043,2614,3352,2667,4513,6472,7471,5720,1616],
+ [8878,1613,1716,868,1906,2681,564,665,5995,2474,7496,3432,9491,9087,8850,8287,669,823,347,6194,2264,2592,7871,7616,8508,4827,760,2676,4660,4881,7572,3811,9032,939,4384,929,7525,8419,5556,9063,662,8887,7026,8534,3111,1454,2082,7598,5726,6687,9647,7608,73,3014,5063,670,5461,5631,3367,9796,8475,7908,5073,1565,5008,5295,4457,1274,4788,1728,338,600,8415,8535,9351,7750,6887,5845,1741,125],
+ [3637,6489,9634,9464,9055,2413,7824,9517,7532,3577,7050,6186,6980,9365,9782,191,870,2497,8498,2218,2757,5420,6468,586,3320,9230,1034,1393,9886,5072,9391,1178,8464,8042,6869,2075,8275,3601,7715,9470,8786,6475,8373,2159,9237,2066,3264,5000,679,355,3069,4073,494,2308,5512,4334,9438,8786,8637,9774,1169,1949,6594,6072,4270,9158,7916,5752,6794,9391,6301,5842,3285,2141,3898,8027,4310,8821,7079,1307],
+ [8497,6681,4732,7151,7060,5204,9030,7157,833,5014,8723,3207,9796,9286,4913,119,5118,7650,9335,809,3675,2597,5144,3945,5090,8384,187,4102,1260,2445,2792,4422,8389,9290,50,1765,1521,6921,8586,4368,1565,5727,7855,2003,4834,9897,5911,8630,5070,1330,7692,7557,7980,6028,5805,9090,8265,3019,3802,698,9149,5748,1965,9658,4417,5994,5584,8226,2937,272,5743,1278,5698,8736,2595,6475,5342,6596,1149,6920],
+ [8188,8009,9546,6310,8772,2500,9846,6592,6872,3857,1307,8125,7042,1544,6159,2330,643,4604,7899,6848,371,8067,2062,3200,7295,1857,9505,6936,384,2193,2190,301,8535,5503,1462,7380,5114,4824,8833,1763,4974,8711,9262,6698,3999,2645,6937,7747,1128,2933,3556,7943,2885,3122,9105,5447,418,2899,5148,3699,9021,9501,597,4084,175,1621,1,1079,6067,5812,4326,9914,6633,5394,4233,6728,9084,1864,5863,1225],
+ [9935,8793,9117,1825,9542,8246,8437,3331,9128,9675,6086,7075,319,1334,7932,3583,7167,4178,1726,7720,695,8277,7887,6359,5912,1719,2780,8529,1359,2013,4498,8072,1129,9998,1147,8804,9405,6255,1619,2165,7491,1,8882,7378,3337,503,5758,4109,3577,985,3200,7615,8058,5032,1080,6410,6873,5496,1466,2412,9885,5904,4406,3605,8770,4361,6205,9193,1537,9959,214,7260,9566,1685,100,4920,7138,9819,5637,976],
+ [3466,9854,985,1078,7222,8888,5466,5379,3578,4540,6853,8690,3728,6351,7147,3134,6921,9692,857,3307,4998,2172,5783,3931,9417,2541,6299,13,787,2099,9131,9494,896,8600,1643,8419,7248,2660,2609,8579,91,6663,5506,7675,1947,6165,4286,1972,9645,3805,1663,1456,8853,5705,9889,7489,1107,383,4044,2969,3343,152,7805,4980,9929,5033,1737,9953,7197,9158,4071,1324,473,9676,3984,9680,3606,8160,7384,5432],
+ [1005,4512,5186,3953,2164,3372,4097,3247,8697,3022,9896,4101,3871,6791,3219,2742,4630,6967,7829,5991,6134,1197,1414,8923,8787,1394,8852,5019,7768,5147,8004,8825,5062,9625,7988,1110,3992,7984,9966,6516,6251,8270,421,3723,1432,4830,6935,8095,9059,2214,6483,6846,3120,1587,6201,6691,9096,9627,6671,4002,3495,9939,7708,7465,5879,6959,6634,3241,3401,2355,9061,2611,7830,3941,2177,2146,5089,7079,519,6351],
+ [7280,8586,4261,2831,7217,3141,9994,9940,5462,2189,4005,6942,9848,5350,8060,6665,7519,4324,7684,657,9453,9296,2944,6843,7499,7847,1728,9681,3906,6353,5529,2822,3355,3897,7724,4257,7489,8672,4356,3983,1948,6892,7415,4153,5893,4190,621,1736,4045,9532,7701,3671,1211,1622,3176,4524,9317,7800,5638,6644,6943,5463,3531,2821,1347,5958,3436,1438,2999,994,850,4131,2616,1549,3465,5946,690,9273,6954,7991],
+ [9517,399,3249,2596,7736,2142,1322,968,7350,1614,468,3346,3265,7222,6086,1661,5317,2582,7959,4685,2807,2917,1037,5698,1529,3972,8716,2634,3301,3412,8621,743,8001,4734,888,7744,8092,3671,8941,1487,5658,7099,2781,99,1932,4443,4756,4652,9328,1581,7855,4312,5976,7255,6480,3996,2748,1973,9731,4530,2790,9417,7186,5303,3557,351,7182,9428,1342,9020,7599,1392,8304,2070,9138,7215,2008,9937,1106,7110],
+ [7444,769,9688,632,1571,6820,8743,4338,337,3366,3073,1946,8219,104,4210,6986,249,5061,8693,7960,6546,1004,8857,5997,9352,4338,6105,5008,2556,6518,6694,4345,3727,7956,20,3954,8652,4424,9387,2035,8358,5962,5304,5194,8650,8282,1256,1103,2138,6679,1985,3653,2770,2433,4278,615,2863,1715,242,3790,2636,6998,3088,1671,2239,957,5411,4595,6282,2881,9974,2401,875,7574,2987,4587,3147,6766,9885,2965],
+ [3287,3016,3619,6818,9073,6120,5423,557,2900,2015,8111,3873,1314,4189,1846,4399,7041,7583,2427,2864,3525,5002,2069,748,1948,6015,2684,438,770,8367,1663,7887,7759,1885,157,7770,4520,4878,3857,1137,3525,3050,6276,5569,7649,904,4533,7843,2199,5648,7628,9075,9441,3600,7231,2388,5640,9096,958,3058,584,5899,8150,1181,9616,1098,8162,6819,8171,1519,1140,7665,8801,2632,1299,9192,707,9955,2710,7314],
+ [1772,2963,7578,3541,3095,1488,7026,2634,6015,4633,4370,2762,1650,2174,909,8158,2922,8467,4198,4280,9092,8856,8835,5457,2790,8574,9742,5054,9547,4156,7940,8126,9824,7340,8840,6574,3547,1477,3014,6798,7134,435,9484,9859,3031,4,1502,4133,1738,1807,4825,463,6343,9701,8506,9822,9555,8688,8168,3467,3234,6318,1787,5591,419,6593,7974,8486,9861,6381,6758,194,3061,4315,2863,4665,3789,2201,1492,4416],
+ [126,8927,6608,5682,8986,6867,1715,6076,3159,788,3140,4744,830,9253,5812,5021,7616,8534,1546,9590,1101,9012,9821,8132,7857,4086,1069,7491,2988,1579,2442,4321,2149,7642,6108,250,6086,3167,24,9528,7663,2685,1220,9196,1397,5776,1577,1730,5481,977,6115,199,6326,2183,3767,5928,5586,7561,663,8649,9688,949,5913,9160,1870,5764,9887,4477,6703,1413,4995,5494,7131,2192,8969,7138,3997,8697,646,1028],
+ [8074,1731,8245,624,4601,8706,155,8891,309,2552,8208,8452,2954,3124,3469,4246,3352,1105,4509,8677,9901,4416,8191,9283,5625,7120,2952,8881,7693,830,4580,8228,9459,8611,4499,1179,4988,1394,550,2336,6089,6872,269,7213,1848,917,6672,4890,656,1478,6536,3165,4743,4990,1176,6211,7207,5284,9730,4738,1549,4986,4942,8645,3698,9429,1439,2175,6549,3058,6513,1574,6988,8333,3406,5245,5431,7140,7085,6407],
+ [7845,4694,2530,8249,290,5948,5509,1588,5940,4495,5866,5021,4626,3979,3296,7589,4854,1998,5627,3926,8346,6512,9608,1918,7070,4747,4182,2858,2766,4606,6269,4107,8982,8568,9053,4244,5604,102,2756,727,5887,2566,7922,44,5986,621,1202,374,6988,4130,3627,6744,9443,4568,1398,8679,397,3928,9159,367,2917,6127,5788,3304,8129,911,2669,1463,9749,264,4478,8940,1109,7309,2462,117,4692,7724,225,2312],
+ [4164,3637,2000,941,8903,39,3443,7172,1031,3687,4901,8082,4945,4515,7204,9310,9349,9535,9940,218,1788,9245,2237,1541,5670,6538,6047,5553,9807,8101,1925,8714,445,8332,7309,6830,5786,5736,7306,2710,3034,1838,7969,6318,7912,2584,2080,7437,6705,2254,7428,820,782,9861,7596,3842,3631,8063,5240,6666,394,4565,7865,4895,9890,6028,6117,4724,9156,4473,4552,602,470,6191,4927,5387,884,3146,1978,3000],
+ [4258,6880,1696,3582,5793,4923,2119,1155,9056,9698,6603,3768,5514,9927,9609,6166,6566,4536,4985,4934,8076,9062,6741,6163,7399,4562,2337,5600,2919,9012,8459,1308,6072,1225,9306,8818,5886,7243,7365,8792,6007,9256,6699,7171,4230,7002,8720,7839,4533,1671,478,7774,1607,2317,5437,4705,7886,4760,6760,7271,3081,2997,3088,7675,6208,3101,6821,6840,122,9633,4900,2067,8546,4549,2091,7188,5605,8599,6758,5229],
+ [7854,5243,9155,3556,8812,7047,2202,1541,5993,4600,4760,713,434,7911,7426,7414,8729,322,803,7960,7563,4908,6285,6291,736,3389,9339,4132,8701,7534,5287,3646,592,3065,7582,2592,8755,6068,8597,1982,5782,1894,2900,6236,4039,6569,3037,5837,7698,700,7815,2491,7272,5878,3083,6778,6639,3589,5010,8313,2581,6617,5869,8402,6808,2951,2321,5195,497,2190,6187,1342,1316,4453,7740,4154,2959,1781,1482,8256],
+ [7178,2046,4419,744,8312,5356,6855,8839,319,2962,5662,47,6307,8662,68,4813,567,2712,9931,1678,3101,8227,6533,4933,6656,92,5846,4780,6256,6361,4323,9985,1231,2175,7178,3034,9744,6155,9165,7787,5836,9318,7860,9644,8941,6480,9443,8188,5928,161,6979,2352,5628,6991,1198,8067,5867,6620,3778,8426,2994,3122,3124,6335,3918,8897,2655,9670,634,1088,1576,8935,7255,474,8166,7417,9547,2886,5560,3842],
+ [6957,3111,26,7530,7143,1295,1744,6057,3009,1854,8098,5405,2234,4874,9447,2620,9303,27,7410,969,40,2966,5648,7596,8637,4238,3143,3679,7187,690,9980,7085,7714,9373,5632,7526,6707,3951,9734,4216,2146,3602,5371,6029,3039,4433,4855,4151,1449,3376,8009,7240,7027,4602,2947,9081,4045,8424,9352,8742,923,2705,4266,3232,2264,6761,363,2651,3383,7770,6730,7856,7340,9679,2158,610,4471,4608,910,6241],
+ [4417,6756,1013,8797,658,8809,5032,8703,7541,846,3357,2920,9817,1745,9980,7593,4667,3087,779,3218,6233,5568,4296,2289,2654,7898,5021,9461,5593,8214,9173,4203,2271,7980,2983,5952,9992,8399,3468,1776,3188,9314,1720,6523,2933,621,8685,5483,8986,6163,3444,9539,4320,155,3992,2828,2150,6071,524,2895,5468,8063,1210,3348,9071,4862,483,9017,4097,6186,9815,3610,5048,1644,1003,9865,9332,2145,1944,2213],
+ [9284,3803,4920,1927,6706,4344,7383,4786,9890,2010,5228,1224,3158,6967,8580,8990,8883,5213,76,8306,2031,4980,5639,9519,7184,5645,7769,3259,8077,9130,1317,3096,9624,3818,1770,695,2454,947,6029,3474,9938,3527,5696,4760,7724,7738,2848,6442,5767,6845,8323,4131,2859,7595,2500,4815,3660,9130,8580,7016,8231,4391,8369,3444,4069,4021,556,6154,627,2778,1496,4206,6356,8434,8491,3816,8231,3190,5575,1015],
+ [3787,7572,1788,6803,5641,6844,1961,4811,8535,9914,9999,1450,8857,738,4662,8569,6679,2225,7839,8618,286,2648,5342,2294,3205,4546,176,8705,3741,6134,8324,8021,7004,5205,7032,6637,9442,5539,5584,4819,5874,5807,8589,6871,9016,983,1758,3786,1519,6241,185,8398,495,3370,9133,3051,4549,9674,7311,9738,3316,9383,2658,2776,9481,7558,619,3943,3324,6491,4933,153,9738,4623,912,3595,7771,7939,1219,4405],
+ [2650,3883,4154,5809,315,7756,4430,1788,4451,1631,6461,7230,6017,5751,138,588,5282,2442,9110,9035,6349,2515,1570,6122,4192,4174,3530,1933,4186,4420,4609,5739,4135,2963,6308,1161,8809,8619,2796,3819,6971,8228,4188,1492,909,8048,2328,6772,8467,7671,9068,2226,7579,6422,7056,8042,3296,2272,3006,2196,7320,3238,3490,3102,37,1293,3212,4767,5041,8773,5794,4456,6174,7279,7054,2835,7053,9088,790,6640],
+ [3101,1057,7057,3826,6077,1025,2955,1224,1114,6729,5902,4698,6239,7203,9423,1804,4417,6686,1426,6941,8071,1029,4985,9010,6122,6597,1622,1574,3513,1684,7086,5505,3244,411,9638,4150,907,9135,829,981,1707,5359,8781,9751,5,9131,3973,7159,1340,6955,7514,7993,6964,8198,1933,2797,877,3993,4453,8020,9349,8646,2779,8679,2961,3547,3374,3510,1129,3568,2241,2625,9138,5974,8206,7669,7678,1833,8700,4480],
+ [4865,9912,8038,8238,782,3095,8199,1127,4501,7280,2112,2487,3626,2790,9432,1475,6312,8277,4827,2218,5806,7132,8752,1468,7471,6386,739,8762,8323,8120,5169,9078,9058,3370,9560,7987,8585,8531,5347,9312,1058,4271,1159,5286,5404,6925,8606,9204,7361,2415,560,586,4002,2644,1927,2824,768,4409,2942,3345,1002,808,4941,6267,7979,5140,8643,7553,9438,7320,4938,2666,4609,2778,8158,6730,3748,3867,1866,7181],
+ [171,3771,7134,8927,4778,2913,3326,2004,3089,7853,1378,1729,4777,2706,9578,1360,5693,3036,1851,7248,2403,2273,8536,6501,9216,613,9671,7131,7719,6425,773,717,8803,160,1114,7554,7197,753,4513,4322,8499,4533,2609,4226,8710,6627,644,9666,6260,4870,5744,7385,6542,6203,7703,6130,8944,5589,2262,6803,6381,7414,6888,5123,7320,9392,9061,6780,322,8975,7050,5089,1061,2260,3199,1150,1865,5386,9699,6501],
+ [3744,8454,6885,8277,919,1923,4001,6864,7854,5519,2491,6057,8794,9645,1776,5714,9786,9281,7538,6916,3215,395,2501,9618,4835,8846,9708,2813,3303,1794,8309,7176,2206,1602,1838,236,4593,2245,8993,4017,10,8215,6921,5206,4023,5932,6997,7801,262,7640,3107,8275,4938,7822,2425,3223,3886,2105,8700,9526,2088,8662,8034,7004,5710,2124,7164,3574,6630,9980,4242,2901,9471,1491,2117,4562,1130,9086,4117,6698],
+ [2810,2280,2331,1170,4554,4071,8387,1215,2274,9848,6738,1604,7281,8805,439,1298,8318,7834,9426,8603,6092,7944,1309,8828,303,3157,4638,4439,9175,1921,4695,7716,1494,1015,1772,5913,1127,1952,1950,8905,4064,9890,385,9357,7945,5035,7082,5369,4093,6546,5187,5637,2041,8946,1758,7111,6566,1027,1049,5148,7224,7248,296,6169,375,1656,7993,2816,3717,4279,4675,1609,3317,42,6201,3100,3144,163,9530,4531],
+ [7096,6070,1009,4988,3538,5801,7149,3063,2324,2912,7911,7002,4338,7880,2481,7368,3516,2016,7556,2193,1388,3865,8125,4637,4096,8114,750,3144,1938,7002,9343,4095,1392,4220,3455,6969,9647,1321,9048,1996,1640,6626,1788,314,9578,6630,2813,6626,4981,9908,7024,4355,3201,3521,3864,3303,464,1923,595,9801,3391,8366,8084,9374,1041,8807,9085,1892,9431,8317,9016,9221,8574,9981,9240,5395,2009,6310,2854,9255],
+ [8830,3145,2960,9615,8220,6061,3452,2918,6481,9278,2297,3385,6565,7066,7316,5682,107,7646,4466,68,1952,9603,8615,54,7191,791,6833,2560,693,9733,4168,570,9127,9537,1925,8287,5508,4297,8452,8795,6213,7994,2420,4208,524,5915,8602,8330,2651,8547,6156,1812,6271,7991,9407,9804,1553,6866,1128,2119,4691,9711,8315,5879,9935,6900,482,682,4126,1041,428,6247,3720,5882,7526,2582,4327,7725,3503,2631],
+ [2738,9323,721,7434,1453,6294,2957,3786,5722,6019,8685,4386,3066,9057,6860,499,5315,3045,5194,7111,3137,9104,941,586,3066,755,4177,8819,7040,5309,3583,3897,4428,7788,4721,7249,6559,7324,825,7311,3760,6064,6070,9672,4882,584,1365,9739,9331,5783,2624,7889,1604,1303,1555,7125,8312,425,8936,3233,7724,1480,403,7440,1784,1754,4721,1569,652,3893,4574,5692,9730,4813,9844,8291,9199,7101,3391,8914],
+ [6044,2928,9332,3328,8588,447,3830,1176,3523,2705,8365,6136,5442,9049,5526,8575,8869,9031,7280,706,2794,8814,5767,4241,7696,78,6570,556,5083,1426,4502,3336,9518,2292,1885,3740,3153,9348,9331,8051,2759,5407,9028,7840,9255,831,515,2612,9747,7435,8964,4971,2048,4900,5967,8271,1719,9670,2810,6777,1594,6367,6259,8316,3815,1689,6840,9437,4361,822,9619,3065,83,6344,7486,8657,8228,9635,6932,4864],
+ [8478,4777,6334,4678,7476,4963,6735,3096,5860,1405,5127,7269,7793,4738,227,9168,2996,8928,765,733,1276,7677,6258,1528,9558,3329,302,8901,1422,8277,6340,645,9125,8869,5952,141,8141,1816,9635,4025,4184,3093,83,2344,2747,9352,7966,1206,1126,1826,218,7939,2957,2729,810,8752,5247,4174,4038,8884,7899,9567,301,5265,5752,7524,4381,1669,3106,8270,6228,6373,754,2547,4240,2313,5514,3022,1040,9738],
+ [2265,8192,1763,1369,8469,8789,4836,52,1212,6690,5257,8918,6723,6319,378,4039,2421,8555,8184,9577,1432,7139,8078,5452,9628,7579,4161,7490,5159,8559,1011,81,478,5840,1964,1334,6875,8670,9900,739,1514,8692,522,9316,6955,1345,8132,2277,3193,9773,3923,4177,2183,1236,6747,6575,4874,6003,6409,8187,745,8776,9440,7543,9825,2582,7381,8147,7236,5185,7564,6125,218,7991,6394,391,7659,7456,5128,5294],
+ [2132,8992,8160,5782,4420,3371,3798,5054,552,5631,7546,4716,1332,6486,7892,7441,4370,6231,4579,2121,8615,1145,9391,1524,1385,2400,9437,2454,7896,7467,2928,8400,3299,4025,7458,4703,7206,6358,792,6200,725,4275,4136,7390,5984,4502,7929,5085,8176,4600,119,3568,76,9363,6943,2248,9077,9731,6213,5817,6729,4190,3092,6910,759,2682,8380,1254,9604,3011,9291,5329,9453,9746,2739,6522,3765,5634,1113,5789],
+ [5304,5499,564,2801,679,2653,1783,3608,7359,7797,3284,796,3222,437,7185,6135,8571,2778,7488,5746,678,6140,861,7750,803,9859,9918,2425,3734,2698,9005,4864,9818,6743,2475,132,9486,3825,5472,919,292,4411,7213,7699,6435,9019,6769,1388,802,2124,1345,8493,9487,8558,7061,8777,8833,2427,2238,5409,4957,8503,3171,7622,5779,6145,2417,5873,5563,5693,9574,9491,1937,7384,4563,6842,5432,2751,3406,7981]
+];
+```
+
+## --seed-contents--
+
+```js
+function pathSumThreeWays(matrix) {
+
+ return true;
+}
+
+// Only change code above this line
+
+const testMatrix1 = [
+ [131, 673, 234, 103, 18],
+ [201, 96, 342, 965, 150],
+ [630, 803, 746, 422, 111],
+ [537, 699, 497, 121, 956],
+ [805, 732, 524, 37, 331]
+];
+
+pathSumThreeWays(testMatrix1);
+```
+
+# --solutions--
+
+```js
+function pathSumThreeWays(matrix) {
+ function makeMinimumMoveFromUpOrRight(row, column) {
+ const curValue = matrix[row][column];
+ if (values[row - 1] > values[row]) {
+ return values[row] + curValue;
+ }
+ return values[row - 1] + curValue;
+ }
+ function isGoingFromDownBetter(row, column) {
+ return values[row] > values[row + 1] + matrix[row][column];
+ }
+
+ const size = matrix.length;
+ const values = [];
+ for (let row = 0; row < size; row++) {
+ values.push(matrix[row][size - 1]);
+ }
+
+ for (let column = size - 2; column >= 0; column--) {
+ values[0] += matrix[0][column];
+
+ for (let row = 1; row < size; row++) {
+ values[row] = makeMinimumMoveFromUpOrRight(row, column);
+ }
+
+ for (let row = size - 2; row >= 0; row--) {
+ if (isGoingFromDownBetter(row, column)) {
+ values[row] = values[row + 1] + matrix[row][column];
+ }
+ }
+ }
+
+ return Math.min(...values);
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-83-path-sum-four-ways.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-83-path-sum-four-ways.md
new file mode 100644
index 00000000000..8d3b60e0c0b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-83-path-sum-four-ways.md
@@ -0,0 +1,215 @@
+---
+id: 5900f3bf1000cf542c50fed2
+title: 'Problem 83: Path sum: four ways'
+challengeType: 1
+forumTopicId: 302197
+dashedName: problem-83-path-sum-four-ways
+---
+
+# --description--
+
+**Note:** This problem is a significantly more challenging version of Problem 81.
+
+In the 5 by 5 matrix below, the minimal path sum from the top left to the bottom right, by moving left, right, up, and down, is indicated in bold red and is equal to `2297`.
+
+ $$\begin{pmatrix} \color{red}{131} & 673 & \color{red}{234} & \color{red}{103} & \color{red}{18}\\\\
+ \color{red}{201} & \color{red}{96} & \color{red}{342} & 965 & \color{red}{150}\\\\ 630 & 803 & 746 & \color{red}{422} & \color{red}{111}\\\\
+ 537 & 699 & 497 & \color{red}{121} & 956\\\\ 805 & 732 & 524 & \color{red}{37} & \color{red}{331} \end{pmatrix}$$
+
+Find the minimal path sum from the top left to the bottom right by moving left, right, up, and down in `matrix`, a 2D array representing a matrix. The maximum matrix size used in tests will be 80 by 80.
+
+# --hints--
+
+`pathSumFourWays(testMatrix1)` should return a number.
+
+```js
+assert(typeof pathSumFourWays(_testMatrix1) === 'number');
+```
+
+`pathSumFourWays(testMatrix1)` should return `2297`.
+
+```js
+assert.strictEqual(pathSumFourWays(_testMatrix1), 2297);
+```
+
+`pathSumFourWays(testMatrix2)` should return `425185`.
+
+```js
+assert.strictEqual(pathSumFourWays(_testMatrix2), 425185);
+```
+
+# --seed--
+
+## --after-user-code--
+
+```js
+const _testMatrix1 = [
+ [131, 673, 234, 103, 18],
+ [201, 96, 342, 965, 150],
+ [630, 803, 746, 422, 111],
+ [537, 699, 497, 121, 956],
+ [805, 732, 524, 37, 331]
+];
+const _testMatrix2 = [
+ [4445,2697,5115,718,2209,2212,654,4348,3079,6821,7668,3276,8874,4190,3785,2752,9473,7817,9137,496,7338,3434,7152,4355,4552,7917,7827,2460,2350,691,3514,5880,3145,7633,7199,3783,5066,7487,3285,1084,8985,760,872,8609,8051,1134,9536,5750,9716,9371,7619,5617,275,9721,2997,2698,1887,8825,6372,3014,2113,7122,7050,6775,5948,2758,1219,3539,348,7989,2735,9862,1263,8089,6401,9462,3168,2758,3748,5870],
+ [1096,20,1318,7586,5167,2642,1443,5741,7621,7030,5526,4244,2348,4641,9827,2448,6918,5883,3737,300,7116,6531,567,5997,3971,6623,820,6148,3287,1874,7981,8424,7672,7575,6797,6717,1078,5008,4051,8795,5820,346,1851,6463,2117,6058,3407,8211,117,4822,1317,4377,4434,5925,8341,4800,1175,4173,690,8978,7470,1295,3799,8724,3509,9849,618,3320,7068,9633,2384,7175,544,6583,1908,9983,481,4187,9353,9377],
+ [9607,7385,521,6084,1364,8983,7623,1585,6935,8551,2574,8267,4781,3834,2764,2084,2669,4656,9343,7709,2203,9328,8004,6192,5856,3555,2260,5118,6504,1839,9227,1259,9451,1388,7909,5733,6968,8519,9973,1663,5315,7571,3035,4325,4283,2304,6438,3815,9213,9806,9536,196,5542,6907,2475,1159,5820,9075,9470,2179,9248,1828,4592,9167,3713,4640,47,3637,309,7344,6955,346,378,9044,8635,7466,5036,9515,6385,9230],
+ [7206,3114,7760,1094,6150,5182,7358,7387,4497,955,101,1478,7777,6966,7010,8417,6453,4955,3496,107,449,8271,131,2948,6185,784,5937,8001,6104,8282,4165,3642,710,2390,575,715,3089,6964,4217,192,5949,7006,715,3328,1152,66,8044,4319,1735,146,4818,5456,6451,4113,1063,4781,6799,602,1504,6245,6550,1417,1343,2363,3785,5448,4545,9371,5420,5068,4613,4882,4241,5043,7873,8042,8434,3939,9256,2187],
+ [3620,8024,577,9997,7377,7682,1314,1158,6282,6310,1896,2509,5436,1732,9480,706,496,101,6232,7375,2207,2306,110,6772,3433,2878,8140,5933,8688,1399,2210,7332,6172,6403,7333,4044,2291,1790,2446,7390,8698,5723,3678,7104,1825,2040,140,3982,4905,4160,2200,5041,2512,1488,2268,1175,7588,8321,8078,7312,977,5257,8465,5068,3453,3096,1651,7906,253,9250,6021,8791,8109,6651,3412,345,4778,5152,4883,7505],
+ [1074,5438,9008,2679,5397,5429,2652,3403,770,9188,4248,2493,4361,8327,9587,707,9525,5913,93,1899,328,2876,3604,673,8576,6908,7659,2544,3359,3883,5273,6587,3065,1749,3223,604,9925,6941,2823,8767,7039,3290,3214,1787,7904,3421,7137,9560,8451,2669,9219,6332,1576,5477,6755,8348,4164,4307,2984,4012,6629,1044,2874,6541,4942,903,1404,9125,5160,8836,4345,2581,460,8438,1538,5507,668,3352,2678,6942],
+ [4295,1176,5596,1521,3061,9868,7037,7129,8933,6659,5947,5063,3653,9447,9245,2679,767,714,116,8558,163,3927,8779,158,5093,2447,5782,3967,1716,931,7772,8164,1117,9244,5783,7776,3846,8862,6014,2330,6947,1777,3112,6008,3491,1906,5952,314,4602,8994,5919,9214,3995,5026,7688,6809,5003,3128,2509,7477,110,8971,3982,8539,2980,4689,6343,5411,2992,5270,5247,9260,2269,7474,1042,7162,5206,1232,4556,4757],
+ [510,3556,5377,1406,5721,4946,2635,7847,4251,8293,8281,6351,4912,287,2870,3380,3948,5322,3840,4738,9563,1906,6298,3234,8959,1562,6297,8835,7861,239,6618,1322,2553,2213,5053,5446,4402,6500,5182,8585,6900,5756,9661,903,5186,7687,5998,7997,8081,8955,4835,6069,2621,1581,732,9564,1082,1853,5442,1342,520,1737,3703,5321,4793,2776,1508,1647,9101,2499,6891,4336,7012,3329,3212,1442,9993,3988,4930,7706],
+ [9444,3401,5891,9716,1228,7107,109,3563,2700,6161,5039,4992,2242,8541,7372,2067,1294,3058,1306,320,8881,5756,9326,411,8650,8824,5495,8282,8397,2000,1228,7817,2099,6473,3571,5994,4447,1299,5991,543,7874,2297,1651,101,2093,3463,9189,6872,6118,872,1008,1779,2805,9084,4048,2123,5877,55,3075,1737,9459,4535,6453,3644,108,5982,4437,5213,1340,6967,9943,5815,669,8074,1838,6979,9132,9315,715,5048],
+ [3327,4030,7177,6336,9933,5296,2621,4785,2755,4832,2512,2118,2244,4407,2170,499,7532,9742,5051,7687,970,6924,3527,4694,5145,1306,2165,5940,2425,8910,3513,1909,6983,346,6377,4304,9330,7203,6605,3709,3346,970,369,9737,5811,4427,9939,3693,8436,5566,1977,3728,2399,3985,8303,2492,5366,9802,9193,7296,1033,5060,9144,2766,1151,7629,5169,5995,58,7619,7565,4208,1713,6279,3209,4908,9224,7409,1325,8540],
+ [6882,1265,1775,3648,4690,959,5837,4520,5394,1378,9485,1360,4018,578,9174,2932,9890,3696,116,1723,1178,9355,7063,1594,1918,8574,7594,7942,1547,6166,7888,354,6932,4651,1010,7759,6905,661,7689,6092,9292,3845,9605,8443,443,8275,5163,7720,7265,6356,7779,1798,1754,5225,6661,1180,8024,5666,88,9153,1840,3508,1193,4445,2648,3538,6243,6375,8107,5902,5423,2520,1122,5015,6113,8859,9370,966,8673,2442],
+ [7338,3423,4723,6533,848,8041,7921,8277,4094,5368,7252,8852,9166,2250,2801,6125,8093,5738,4038,9808,7359,9494,601,9116,4946,2702,5573,2921,9862,1462,1269,2410,4171,2709,7508,6241,7522,615,2407,8200,4189,5492,5649,7353,2590,5203,4274,710,7329,9063,956,8371,3722,4253,4785,1194,4828,4717,4548,940,983,2575,4511,2938,1827,2027,2700,1236,841,5760,1680,6260,2373,3851,1841,4968,1172,5179,7175,3509],
+ [4420,1327,3560,2376,6260,2988,9537,4064,4829,8872,9598,3228,1792,7118,9962,9336,4368,9189,6857,1829,9863,6287,7303,7769,2707,8257,2391,2009,3975,4993,3068,9835,3427,341,8412,2134,4034,8511,6421,3041,9012,2983,7289,100,1355,7904,9186,6920,5856,2008,6545,8331,3655,5011,839,8041,9255,6524,3862,8788,62,7455,3513,5003,8413,3918,2076,7960,6108,3638,6999,3436,1441,4858,4181,1866,8731,7745,3744,1000],
+ [356,8296,8325,1058,1277,4743,3850,2388,6079,6462,2815,5620,8495,5378,75,4324,3441,9870,1113,165,1544,1179,2834,562,6176,2313,6836,8839,2986,9454,5199,6888,1927,5866,8760,320,1792,8296,7898,6121,7241,5886,5814,2815,8336,1576,4314,3109,2572,6011,2086,9061,9403,3947,5487,9731,7281,3159,1819,1334,3181,5844,5114,9898,4634,2531,4412,6430,4262,8482,4546,4555,6804,2607,9421,686,8649,8860,7794,6672],
+ [9870,152,1558,4963,8750,4754,6521,6256,8818,5208,5691,9659,8377,9725,5050,5343,2539,6101,1844,9700,7750,8114,5357,3001,8830,4438,199,9545,8496,43,2078,327,9397,106,6090,8181,8646,6414,7499,5450,4850,6273,5014,4131,7639,3913,6571,8534,9703,4391,7618,445,1320,5,1894,6771,7383,9191,4708,9706,6939,7937,8726,9382,5216,3685,2247,9029,8154,1738,9984,2626,9438,4167,6351,5060,29,1218,1239,4785],
+ [192,5213,8297,8974,4032,6966,5717,1179,6523,4679,9513,1481,3041,5355,9303,9154,1389,8702,6589,7818,6336,3539,5538,3094,6646,6702,6266,2759,4608,4452,617,9406,8064,6379,444,5602,4950,1810,8391,1536,316,8714,1178,5182,5863,5110,5372,4954,1978,2971,5680,4863,2255,4630,5723,2168,538,1692,1319,7540,440,6430,6266,7712,7385,5702,620,641,3136,7350,1478,3155,2820,9109,6261,1122,4470,14,8493,2095],
+ [1046,4301,6082,474,4974,7822,2102,5161,5172,6946,8074,9716,6586,9962,9749,5015,2217,995,5388,4402,7652,6399,6539,1349,8101,3677,1328,9612,7922,2879,231,5887,2655,508,4357,4964,3554,5930,6236,7384,4614,280,3093,9600,2110,7863,2631,6626,6620,68,1311,7198,7561,1768,5139,1431,221,230,2940,968,5283,6517,2146,1646,869,9402,7068,8645,7058,1765,9690,4152,2926,9504,2939,7504,6074,2944,6470,7859],
+ [4659,736,4951,9344,1927,6271,8837,8711,3241,6579,7660,5499,5616,3743,5801,4682,9748,8796,779,1833,4549,8138,4026,775,4170,2432,4174,3741,7540,8017,2833,4027,396,811,2871,1150,9809,2719,9199,8504,1224,540,2051,3519,7982,7367,2761,308,3358,6505,2050,4836,5090,7864,805,2566,2409,6876,3361,8622,5572,5895,3280,441,7893,8105,1634,2929,274,3926,7786,6123,8233,9921,2674,5340,1445,203,4585,3837],
+ [5759,338,7444,7968,7742,3755,1591,4839,1705,650,7061,2461,9230,9391,9373,2413,1213,431,7801,4994,2380,2703,6161,6878,8331,2538,6093,1275,5065,5062,2839,582,1014,8109,3525,1544,1569,8622,7944,2905,6120,1564,1839,5570,7579,1318,2677,5257,4418,5601,7935,7656,5192,1864,5886,6083,5580,6202,8869,1636,7907,4759,9082,5854,3185,7631,6854,5872,5632,5280,1431,2077,9717,7431,4256,8261,9680,4487,4752,4286],
+ [1571,1428,8599,1230,7772,4221,8523,9049,4042,8726,7567,6736,9033,2104,4879,4967,6334,6716,3994,1269,8995,6539,3610,7667,6560,6065,874,848,4597,1711,7161,4811,6734,5723,6356,6026,9183,2586,5636,1092,7779,7923,8747,6887,7505,9909,1792,3233,4526,3176,1508,8043,720,5212,6046,4988,709,5277,8256,3642,1391,5803,1468,2145,3970,6301,7767,2359,8487,9771,8785,7520,856,1605,8972,2402,2386,991,1383,5963],
+ [1822,4824,5957,6511,9868,4113,301,9353,6228,2881,2966,6956,9124,9574,9233,1601,7340,973,9396,540,4747,8590,9535,3650,7333,7583,4806,3593,2738,8157,5215,8472,2284,9473,3906,6982,5505,6053,7936,6074,7179,6688,1564,1103,6860,5839,2022,8490,910,7551,7805,881,7024,1855,9448,4790,1274,3672,2810,774,7623,4223,4850,6071,9975,4935,1915,9771,6690,3846,517,463,7624,4511,614,6394,3661,7409,1395,8127],
+ [8738,3850,9555,3695,4383,2378,87,6256,6740,7682,9546,4255,6105,2000,1851,4073,8957,9022,6547,5189,2487,303,9602,7833,1628,4163,6678,3144,8589,7096,8913,5823,4890,7679,1212,9294,5884,2972,3012,3359,7794,7428,1579,4350,7246,4301,7779,7790,3294,9547,4367,3549,1958,8237,6758,3497,3250,3456,6318,1663,708,7714,6143,6890,3428,6853,9334,7992,591,6449,9786,1412,8500,722,5468,1371,108,3939,4199,2535],
+ [7047,4323,1934,5163,4166,461,3544,2767,6554,203,6098,2265,9078,2075,4644,6641,8412,9183,487,101,7566,5622,1975,5726,2920,5374,7779,5631,3753,3725,2672,3621,4280,1162,5812,345,8173,9785,1525,955,5603,2215,2580,5261,2765,2990,5979,389,3907,2484,1232,5933,5871,3304,1138,1616,5114,9199,5072,7442,7245,6472,4760,6359,9053,7876,2564,9404,3043,9026,2261,3374,4460,7306,2326,966,828,3274,1712,3446],
+ [3975,4565,8131,5800,4570,2306,8838,4392,9147,11,3911,7118,9645,4994,2028,6062,5431,2279,8752,2658,7836,994,7316,5336,7185,3289,1898,9689,2331,5737,3403,1124,2679,3241,7748,16,2724,5441,6640,9368,9081,5618,858,4969,17,2103,6035,8043,7475,2181,939,415,1617,8500,8253,2155,7843,7974,7859,1746,6336,3193,2617,8736,4079,6324,6645,8891,9396,5522,6103,1857,8979,3835,2475,1310,7422,610,8345,7615],
+ [9248,5397,5686,2988,3446,4359,6634,9141,497,9176,6773,7448,1907,8454,916,1596,2241,1626,1384,2741,3649,5362,8791,7170,2903,2475,5325,6451,924,3328,522,90,4813,9737,9557,691,2388,1383,4021,1609,9206,4707,5200,7107,8104,4333,9860,5013,1224,6959,8527,1877,4545,7772,6268,621,4915,9349,5970,706,9583,3071,4127,780,8231,3017,9114,3836,7503,2383,1977,4870,8035,2379,9704,1037,3992,3642,1016,4303],
+ [5093,138,4639,6609,1146,5565,95,7521,9077,2272,974,4388,2465,2650,722,4998,3567,3047,921,2736,7855,173,2065,4238,1048,5,6847,9548,8632,9194,5942,4777,7910,8971,6279,7253,2516,1555,1833,3184,9453,9053,6897,7808,8629,4877,1871,8055,4881,7639,1537,7701,2508,7564,5845,5023,2304,5396,3193,2955,1088,3801,6203,1748,3737,1276,13,4120,7715,8552,3047,2921,106,7508,304,1280,7140,2567,9135,5266],
+ [6237,4607,7527,9047,522,7371,4883,2540,5867,6366,5301,1570,421,276,3361,527,6637,4861,2401,7522,5808,9371,5298,2045,5096,5447,7755,5115,7060,8529,4078,1943,1697,1764,5453,7085,960,2405,739,2100,5800,728,9737,5704,5693,1431,8979,6428,673,7540,6,7773,5857,6823,150,5869,8486,684,5816,9626,7451,5579,8260,3397,5322,6920,1879,2127,2884,5478,4977,9016,6165,6292,3062,5671,5968,78,4619,4763],
+ [9905,7127,9390,5185,6923,3721,9164,9705,4341,1031,1046,5127,7376,6528,3248,4941,1178,7889,3364,4486,5358,9402,9158,8600,1025,874,1839,1783,309,9030,1843,845,8398,1433,7118,70,8071,2877,3904,8866,6722,4299,10,1929,5897,4188,600,1889,3325,2485,6473,4474,7444,6992,4846,6166,4441,2283,2629,4352,7775,1101,2214,9985,215,8270,9750,2740,8361,7103,5930,8664,9690,8302,9267,344,2077,1372,1880,9550],
+ [5825,8517,7769,2405,8204,1060,3603,7025,478,8334,1997,3692,7433,9101,7294,7498,9415,5452,3850,3508,6857,9213,6807,4412,7310,854,5384,686,4978,892,8651,3241,2743,3801,3813,8588,6701,4416,6990,6490,3197,6838,6503,114,8343,5844,8646,8694,65,791,5979,2687,2621,2019,8097,1423,3644,9764,4921,3266,3662,5561,2476,8271,8138,6147,1168,3340,1998,9874,6572,9873,6659,5609,2711,3931,9567,4143,7833,8887],
+ [6223,2099,2700,589,4716,8333,1362,5007,2753,2848,4441,8397,7192,8191,4916,9955,6076,3370,6396,6971,3156,248,3911,2488,4930,2458,7183,5455,170,6809,6417,3390,1956,7188,577,7526,2203,968,8164,479,8699,7915,507,6393,4632,1597,7534,3604,618,3280,6061,9793,9238,8347,568,9645,2070,5198,6482,5000,9212,6655,5961,7513,1323,3872,6170,3812,4146,2736,67,3151,5548,2781,9679,7564,5043,8587,1893,4531],
+ [5826,3690,6724,2121,9308,6986,8106,6659,2142,1642,7170,2877,5757,6494,8026,6571,8387,9961,6043,9758,9607,6450,8631,8334,7359,5256,8523,2225,7487,1977,9555,8048,5763,2414,4948,4265,2427,8978,8088,8841,9208,9601,5810,9398,8866,9138,4176,5875,7212,3272,6759,5678,7649,4922,5422,1343,8197,3154,3600,687,1028,4579,2084,9467,4492,7262,7296,6538,7657,7134,2077,1505,7332,6890,8964,4879,7603,7400,5973,739],
+ [1861,1613,4879,1884,7334,966,2000,7489,2123,4287,1472,3263,4726,9203,1040,4103,6075,6049,330,9253,4062,4268,1635,9960,577,1320,3195,9628,1030,4092,4979,6474,6393,2799,6967,8687,7724,7392,9927,2085,3200,6466,8702,265,7646,8665,7986,7266,4574,6587,612,2724,704,3191,8323,9523,3002,704,5064,3960,8209,2027,2758,8393,4875,4641,9584,6401,7883,7014,768,443,5490,7506,1852,2005,8850,5776,4487,4269],
+ [4052,6687,4705,7260,6645,6715,3706,5504,8672,2853,1136,8187,8203,4016,871,1809,1366,4952,9294,5339,6872,2645,6083,7874,3056,5218,7485,8796,7401,3348,2103,426,8572,4163,9171,3176,948,7654,9344,3217,1650,5580,7971,2622,76,2874,880,2034,9929,1546,2659,5811,3754,7096,7436,9694,9960,7415,2164,953,2360,4194,2397,1047,2196,6827,575,784,2675,8821,6802,7972,5996,6699,2134,7577,2887,1412,4349,4380],
+ [4629,2234,6240,8132,7592,3181,6389,1214,266,1910,2451,8784,2790,1127,6932,1447,8986,2492,5476,397,889,3027,7641,5083,5776,4022,185,3364,5701,2442,2840,4160,9525,4828,6602,2614,7447,3711,4505,7745,8034,6514,4907,2605,7753,6958,7270,6936,3006,8968,439,2326,4652,3085,3425,9863,5049,5361,8688,297,7580,8777,7916,6687,8683,7141,306,9569,2384,1500,3346,4601,7329,9040,6097,2727,6314,4501,4974,2829],
+ [8316,4072,2025,6884,3027,1808,5714,7624,7880,8528,4205,8686,7587,3230,1139,7273,6163,6986,3914,9309,1464,9359,4474,7095,2212,7302,2583,9462,7532,6567,1606,4436,8981,5612,6796,4385,5076,2007,6072,3678,8331,1338,3299,8845,4783,8613,4071,1232,6028,2176,3990,2148,3748,103,9453,538,6745,9110,926,3125,473,5970,8728,7072,9062,1404,1317,5139,9862,6496,6062,3338,464,1600,2532,1088,8232,7739,8274,3873],
+ [2341,523,7096,8397,8301,6541,9844,244,4993,2280,7689,4025,4196,5522,7904,6048,2623,9258,2149,9461,6448,8087,7245,1917,8340,7127,8466,5725,6996,3421,5313,512,9164,9837,9794,8369,4185,1488,7210,1524,1016,4620,9435,2478,7765,8035,697,6677,3724,6988,5853,7662,3895,9593,1185,4727,6025,5734,7665,3070,138,8469,6748,6459,561,7935,8646,2378,462,7755,3115,9690,8877,3946,2728,8793,244,6323,8666,4271],
+ [6430,2406,8994,56,1267,3826,9443,7079,7579,5232,6691,3435,6718,5698,4144,7028,592,2627,217,734,6194,8156,9118,58,2640,8069,4127,3285,694,3197,3377,4143,4802,3324,8134,6953,7625,3598,3584,4289,7065,3434,2106,7132,5802,7920,9060,7531,3321,1725,1067,3751,444,5503,6785,7937,6365,4803,198,6266,8177,1470,6390,1606,2904,7555,9834,8667,2033,1723,5167,1666,8546,8152,473,4475,6451,7947,3062,3281],
+ [2810,3042,7759,1741,2275,2609,7676,8640,4117,1958,7500,8048,1757,3954,9270,1971,4796,2912,660,5511,3553,1012,5757,4525,6084,7198,8352,5775,7726,8591,7710,9589,3122,4392,6856,5016,749,2285,3356,7482,9956,7348,2599,8944,495,3462,3578,551,4543,7207,7169,7796,1247,4278,6916,8176,3742,8385,2310,1345,8692,2667,4568,1770,8319,3585,4920,3890,4928,7343,5385,9772,7947,8786,2056,9266,3454,2807,877,2660],
+ [6206,8252,5928,5837,4177,4333,207,7934,5581,9526,8906,1498,8411,2984,5198,5134,2464,8435,8514,8674,3876,599,5327,826,2152,4084,2433,9327,9697,4800,2728,3608,3849,3861,3498,9943,1407,3991,7191,9110,5666,8434,4704,6545,5944,2357,1163,4995,9619,6754,4200,9682,6654,4862,4744,5953,6632,1054,293,9439,8286,2255,696,8709,1533,1844,6441,430,1999,6063,9431,7018,8057,2920,6266,6799,356,3597,4024,6665],
+ [3847,6356,8541,7225,2325,2946,5199,469,5450,7508,2197,9915,8284,7983,6341,3276,3321,16,1321,7608,5015,3362,8491,6968,6818,797,156,2575,706,9516,5344,5457,9210,5051,8099,1617,9951,7663,8253,9683,2670,1261,4710,1068,8753,4799,1228,2621,3275,6188,4699,1791,9518,8701,5932,4275,6011,9877,2933,4182,6059,2930,6687,6682,9771,654,9437,3169,8596,1827,5471,8909,2352,123,4394,3208,8756,5513,6917,2056],
+ [5458,8173,3138,3290,4570,4892,3317,4251,9699,7973,1163,1935,5477,6648,9614,5655,9592,975,9118,2194,7322,8248,8413,3462,8560,1907,7810,6650,7355,2939,4973,6894,3933,3784,3200,2419,9234,4747,2208,2207,1945,2899,1407,6145,8023,3484,5688,7686,2737,3828,3704,9004,5190,9740,8643,8650,5358,4426,1522,1707,3613,9887,6956,2447,2762,833,1449,9489,2573,1080,4167,3456,6809,2466,227,7125,2759,6250,6472,8089],
+ [3266,7025,9756,3914,1265,9116,7723,9788,6805,5493,2092,8688,6592,9173,4431,4028,6007,7131,4446,4815,3648,6701,759,3312,8355,4485,4187,5188,8746,7759,3528,2177,5243,8379,3838,7233,4607,9187,7216,2190,6967,2920,6082,7910,5354,3609,8958,6949,7731,494,8753,8707,1523,4426,3543,7085,647,6771,9847,646,5049,824,8417,5260,2730,5702,2513,9275,4279,2767,8684,1165,9903,4518,55,9682,8963,6005,2102,6523],
+ [1998,8731,936,1479,5259,7064,4085,91,7745,7136,3773,3810,730,8255,2705,2653,9790,6807,2342,355,9344,2668,3690,2028,9679,8102,574,4318,6481,9175,5423,8062,2867,9657,7553,3442,3920,7430,3945,7639,3714,3392,2525,4995,4850,2867,7951,9667,486,9506,9888,781,8866,1702,3795,90,356,1483,4200,2131,6969,5931,486,6880,4404,1084,5169,4910,6567,8335,4686,5043,2614,3352,2667,4513,6472,7471,5720,1616],
+ [8878,1613,1716,868,1906,2681,564,665,5995,2474,7496,3432,9491,9087,8850,8287,669,823,347,6194,2264,2592,7871,7616,8508,4827,760,2676,4660,4881,7572,3811,9032,939,4384,929,7525,8419,5556,9063,662,8887,7026,8534,3111,1454,2082,7598,5726,6687,9647,7608,73,3014,5063,670,5461,5631,3367,9796,8475,7908,5073,1565,5008,5295,4457,1274,4788,1728,338,600,8415,8535,9351,7750,6887,5845,1741,125],
+ [3637,6489,9634,9464,9055,2413,7824,9517,7532,3577,7050,6186,6980,9365,9782,191,870,2497,8498,2218,2757,5420,6468,586,3320,9230,1034,1393,9886,5072,9391,1178,8464,8042,6869,2075,8275,3601,7715,9470,8786,6475,8373,2159,9237,2066,3264,5000,679,355,3069,4073,494,2308,5512,4334,9438,8786,8637,9774,1169,1949,6594,6072,4270,9158,7916,5752,6794,9391,6301,5842,3285,2141,3898,8027,4310,8821,7079,1307],
+ [8497,6681,4732,7151,7060,5204,9030,7157,833,5014,8723,3207,9796,9286,4913,119,5118,7650,9335,809,3675,2597,5144,3945,5090,8384,187,4102,1260,2445,2792,4422,8389,9290,50,1765,1521,6921,8586,4368,1565,5727,7855,2003,4834,9897,5911,8630,5070,1330,7692,7557,7980,6028,5805,9090,8265,3019,3802,698,9149,5748,1965,9658,4417,5994,5584,8226,2937,272,5743,1278,5698,8736,2595,6475,5342,6596,1149,6920],
+ [8188,8009,9546,6310,8772,2500,9846,6592,6872,3857,1307,8125,7042,1544,6159,2330,643,4604,7899,6848,371,8067,2062,3200,7295,1857,9505,6936,384,2193,2190,301,8535,5503,1462,7380,5114,4824,8833,1763,4974,8711,9262,6698,3999,2645,6937,7747,1128,2933,3556,7943,2885,3122,9105,5447,418,2899,5148,3699,9021,9501,597,4084,175,1621,1,1079,6067,5812,4326,9914,6633,5394,4233,6728,9084,1864,5863,1225],
+ [9935,8793,9117,1825,9542,8246,8437,3331,9128,9675,6086,7075,319,1334,7932,3583,7167,4178,1726,7720,695,8277,7887,6359,5912,1719,2780,8529,1359,2013,4498,8072,1129,9998,1147,8804,9405,6255,1619,2165,7491,1,8882,7378,3337,503,5758,4109,3577,985,3200,7615,8058,5032,1080,6410,6873,5496,1466,2412,9885,5904,4406,3605,8770,4361,6205,9193,1537,9959,214,7260,9566,1685,100,4920,7138,9819,5637,976],
+ [3466,9854,985,1078,7222,8888,5466,5379,3578,4540,6853,8690,3728,6351,7147,3134,6921,9692,857,3307,4998,2172,5783,3931,9417,2541,6299,13,787,2099,9131,9494,896,8600,1643,8419,7248,2660,2609,8579,91,6663,5506,7675,1947,6165,4286,1972,9645,3805,1663,1456,8853,5705,9889,7489,1107,383,4044,2969,3343,152,7805,4980,9929,5033,1737,9953,7197,9158,4071,1324,473,9676,3984,9680,3606,8160,7384,5432],
+ [1005,4512,5186,3953,2164,3372,4097,3247,8697,3022,9896,4101,3871,6791,3219,2742,4630,6967,7829,5991,6134,1197,1414,8923,8787,1394,8852,5019,7768,5147,8004,8825,5062,9625,7988,1110,3992,7984,9966,6516,6251,8270,421,3723,1432,4830,6935,8095,9059,2214,6483,6846,3120,1587,6201,6691,9096,9627,6671,4002,3495,9939,7708,7465,5879,6959,6634,3241,3401,2355,9061,2611,7830,3941,2177,2146,5089,7079,519,6351],
+ [7280,8586,4261,2831,7217,3141,9994,9940,5462,2189,4005,6942,9848,5350,8060,6665,7519,4324,7684,657,9453,9296,2944,6843,7499,7847,1728,9681,3906,6353,5529,2822,3355,3897,7724,4257,7489,8672,4356,3983,1948,6892,7415,4153,5893,4190,621,1736,4045,9532,7701,3671,1211,1622,3176,4524,9317,7800,5638,6644,6943,5463,3531,2821,1347,5958,3436,1438,2999,994,850,4131,2616,1549,3465,5946,690,9273,6954,7991],
+ [9517,399,3249,2596,7736,2142,1322,968,7350,1614,468,3346,3265,7222,6086,1661,5317,2582,7959,4685,2807,2917,1037,5698,1529,3972,8716,2634,3301,3412,8621,743,8001,4734,888,7744,8092,3671,8941,1487,5658,7099,2781,99,1932,4443,4756,4652,9328,1581,7855,4312,5976,7255,6480,3996,2748,1973,9731,4530,2790,9417,7186,5303,3557,351,7182,9428,1342,9020,7599,1392,8304,2070,9138,7215,2008,9937,1106,7110],
+ [7444,769,9688,632,1571,6820,8743,4338,337,3366,3073,1946,8219,104,4210,6986,249,5061,8693,7960,6546,1004,8857,5997,9352,4338,6105,5008,2556,6518,6694,4345,3727,7956,20,3954,8652,4424,9387,2035,8358,5962,5304,5194,8650,8282,1256,1103,2138,6679,1985,3653,2770,2433,4278,615,2863,1715,242,3790,2636,6998,3088,1671,2239,957,5411,4595,6282,2881,9974,2401,875,7574,2987,4587,3147,6766,9885,2965],
+ [3287,3016,3619,6818,9073,6120,5423,557,2900,2015,8111,3873,1314,4189,1846,4399,7041,7583,2427,2864,3525,5002,2069,748,1948,6015,2684,438,770,8367,1663,7887,7759,1885,157,7770,4520,4878,3857,1137,3525,3050,6276,5569,7649,904,4533,7843,2199,5648,7628,9075,9441,3600,7231,2388,5640,9096,958,3058,584,5899,8150,1181,9616,1098,8162,6819,8171,1519,1140,7665,8801,2632,1299,9192,707,9955,2710,7314],
+ [1772,2963,7578,3541,3095,1488,7026,2634,6015,4633,4370,2762,1650,2174,909,8158,2922,8467,4198,4280,9092,8856,8835,5457,2790,8574,9742,5054,9547,4156,7940,8126,9824,7340,8840,6574,3547,1477,3014,6798,7134,435,9484,9859,3031,4,1502,4133,1738,1807,4825,463,6343,9701,8506,9822,9555,8688,8168,3467,3234,6318,1787,5591,419,6593,7974,8486,9861,6381,6758,194,3061,4315,2863,4665,3789,2201,1492,4416],
+ [126,8927,6608,5682,8986,6867,1715,6076,3159,788,3140,4744,830,9253,5812,5021,7616,8534,1546,9590,1101,9012,9821,8132,7857,4086,1069,7491,2988,1579,2442,4321,2149,7642,6108,250,6086,3167,24,9528,7663,2685,1220,9196,1397,5776,1577,1730,5481,977,6115,199,6326,2183,3767,5928,5586,7561,663,8649,9688,949,5913,9160,1870,5764,9887,4477,6703,1413,4995,5494,7131,2192,8969,7138,3997,8697,646,1028],
+ [8074,1731,8245,624,4601,8706,155,8891,309,2552,8208,8452,2954,3124,3469,4246,3352,1105,4509,8677,9901,4416,8191,9283,5625,7120,2952,8881,7693,830,4580,8228,9459,8611,4499,1179,4988,1394,550,2336,6089,6872,269,7213,1848,917,6672,4890,656,1478,6536,3165,4743,4990,1176,6211,7207,5284,9730,4738,1549,4986,4942,8645,3698,9429,1439,2175,6549,3058,6513,1574,6988,8333,3406,5245,5431,7140,7085,6407],
+ [7845,4694,2530,8249,290,5948,5509,1588,5940,4495,5866,5021,4626,3979,3296,7589,4854,1998,5627,3926,8346,6512,9608,1918,7070,4747,4182,2858,2766,4606,6269,4107,8982,8568,9053,4244,5604,102,2756,727,5887,2566,7922,44,5986,621,1202,374,6988,4130,3627,6744,9443,4568,1398,8679,397,3928,9159,367,2917,6127,5788,3304,8129,911,2669,1463,9749,264,4478,8940,1109,7309,2462,117,4692,7724,225,2312],
+ [4164,3637,2000,941,8903,39,3443,7172,1031,3687,4901,8082,4945,4515,7204,9310,9349,9535,9940,218,1788,9245,2237,1541,5670,6538,6047,5553,9807,8101,1925,8714,445,8332,7309,6830,5786,5736,7306,2710,3034,1838,7969,6318,7912,2584,2080,7437,6705,2254,7428,820,782,9861,7596,3842,3631,8063,5240,6666,394,4565,7865,4895,9890,6028,6117,4724,9156,4473,4552,602,470,6191,4927,5387,884,3146,1978,3000],
+ [4258,6880,1696,3582,5793,4923,2119,1155,9056,9698,6603,3768,5514,9927,9609,6166,6566,4536,4985,4934,8076,9062,6741,6163,7399,4562,2337,5600,2919,9012,8459,1308,6072,1225,9306,8818,5886,7243,7365,8792,6007,9256,6699,7171,4230,7002,8720,7839,4533,1671,478,7774,1607,2317,5437,4705,7886,4760,6760,7271,3081,2997,3088,7675,6208,3101,6821,6840,122,9633,4900,2067,8546,4549,2091,7188,5605,8599,6758,5229],
+ [7854,5243,9155,3556,8812,7047,2202,1541,5993,4600,4760,713,434,7911,7426,7414,8729,322,803,7960,7563,4908,6285,6291,736,3389,9339,4132,8701,7534,5287,3646,592,3065,7582,2592,8755,6068,8597,1982,5782,1894,2900,6236,4039,6569,3037,5837,7698,700,7815,2491,7272,5878,3083,6778,6639,3589,5010,8313,2581,6617,5869,8402,6808,2951,2321,5195,497,2190,6187,1342,1316,4453,7740,4154,2959,1781,1482,8256],
+ [7178,2046,4419,744,8312,5356,6855,8839,319,2962,5662,47,6307,8662,68,4813,567,2712,9931,1678,3101,8227,6533,4933,6656,92,5846,4780,6256,6361,4323,9985,1231,2175,7178,3034,9744,6155,9165,7787,5836,9318,7860,9644,8941,6480,9443,8188,5928,161,6979,2352,5628,6991,1198,8067,5867,6620,3778,8426,2994,3122,3124,6335,3918,8897,2655,9670,634,1088,1576,8935,7255,474,8166,7417,9547,2886,5560,3842],
+ [6957,3111,26,7530,7143,1295,1744,6057,3009,1854,8098,5405,2234,4874,9447,2620,9303,27,7410,969,40,2966,5648,7596,8637,4238,3143,3679,7187,690,9980,7085,7714,9373,5632,7526,6707,3951,9734,4216,2146,3602,5371,6029,3039,4433,4855,4151,1449,3376,8009,7240,7027,4602,2947,9081,4045,8424,9352,8742,923,2705,4266,3232,2264,6761,363,2651,3383,7770,6730,7856,7340,9679,2158,610,4471,4608,910,6241],
+ [4417,6756,1013,8797,658,8809,5032,8703,7541,846,3357,2920,9817,1745,9980,7593,4667,3087,779,3218,6233,5568,4296,2289,2654,7898,5021,9461,5593,8214,9173,4203,2271,7980,2983,5952,9992,8399,3468,1776,3188,9314,1720,6523,2933,621,8685,5483,8986,6163,3444,9539,4320,155,3992,2828,2150,6071,524,2895,5468,8063,1210,3348,9071,4862,483,9017,4097,6186,9815,3610,5048,1644,1003,9865,9332,2145,1944,2213],
+ [9284,3803,4920,1927,6706,4344,7383,4786,9890,2010,5228,1224,3158,6967,8580,8990,8883,5213,76,8306,2031,4980,5639,9519,7184,5645,7769,3259,8077,9130,1317,3096,9624,3818,1770,695,2454,947,6029,3474,9938,3527,5696,4760,7724,7738,2848,6442,5767,6845,8323,4131,2859,7595,2500,4815,3660,9130,8580,7016,8231,4391,8369,3444,4069,4021,556,6154,627,2778,1496,4206,6356,8434,8491,3816,8231,3190,5575,1015],
+ [3787,7572,1788,6803,5641,6844,1961,4811,8535,9914,9999,1450,8857,738,4662,8569,6679,2225,7839,8618,286,2648,5342,2294,3205,4546,176,8705,3741,6134,8324,8021,7004,5205,7032,6637,9442,5539,5584,4819,5874,5807,8589,6871,9016,983,1758,3786,1519,6241,185,8398,495,3370,9133,3051,4549,9674,7311,9738,3316,9383,2658,2776,9481,7558,619,3943,3324,6491,4933,153,9738,4623,912,3595,7771,7939,1219,4405],
+ [2650,3883,4154,5809,315,7756,4430,1788,4451,1631,6461,7230,6017,5751,138,588,5282,2442,9110,9035,6349,2515,1570,6122,4192,4174,3530,1933,4186,4420,4609,5739,4135,2963,6308,1161,8809,8619,2796,3819,6971,8228,4188,1492,909,8048,2328,6772,8467,7671,9068,2226,7579,6422,7056,8042,3296,2272,3006,2196,7320,3238,3490,3102,37,1293,3212,4767,5041,8773,5794,4456,6174,7279,7054,2835,7053,9088,790,6640],
+ [3101,1057,7057,3826,6077,1025,2955,1224,1114,6729,5902,4698,6239,7203,9423,1804,4417,6686,1426,6941,8071,1029,4985,9010,6122,6597,1622,1574,3513,1684,7086,5505,3244,411,9638,4150,907,9135,829,981,1707,5359,8781,9751,5,9131,3973,7159,1340,6955,7514,7993,6964,8198,1933,2797,877,3993,4453,8020,9349,8646,2779,8679,2961,3547,3374,3510,1129,3568,2241,2625,9138,5974,8206,7669,7678,1833,8700,4480],
+ [4865,9912,8038,8238,782,3095,8199,1127,4501,7280,2112,2487,3626,2790,9432,1475,6312,8277,4827,2218,5806,7132,8752,1468,7471,6386,739,8762,8323,8120,5169,9078,9058,3370,9560,7987,8585,8531,5347,9312,1058,4271,1159,5286,5404,6925,8606,9204,7361,2415,560,586,4002,2644,1927,2824,768,4409,2942,3345,1002,808,4941,6267,7979,5140,8643,7553,9438,7320,4938,2666,4609,2778,8158,6730,3748,3867,1866,7181],
+ [171,3771,7134,8927,4778,2913,3326,2004,3089,7853,1378,1729,4777,2706,9578,1360,5693,3036,1851,7248,2403,2273,8536,6501,9216,613,9671,7131,7719,6425,773,717,8803,160,1114,7554,7197,753,4513,4322,8499,4533,2609,4226,8710,6627,644,9666,6260,4870,5744,7385,6542,6203,7703,6130,8944,5589,2262,6803,6381,7414,6888,5123,7320,9392,9061,6780,322,8975,7050,5089,1061,2260,3199,1150,1865,5386,9699,6501],
+ [3744,8454,6885,8277,919,1923,4001,6864,7854,5519,2491,6057,8794,9645,1776,5714,9786,9281,7538,6916,3215,395,2501,9618,4835,8846,9708,2813,3303,1794,8309,7176,2206,1602,1838,236,4593,2245,8993,4017,10,8215,6921,5206,4023,5932,6997,7801,262,7640,3107,8275,4938,7822,2425,3223,3886,2105,8700,9526,2088,8662,8034,7004,5710,2124,7164,3574,6630,9980,4242,2901,9471,1491,2117,4562,1130,9086,4117,6698],
+ [2810,2280,2331,1170,4554,4071,8387,1215,2274,9848,6738,1604,7281,8805,439,1298,8318,7834,9426,8603,6092,7944,1309,8828,303,3157,4638,4439,9175,1921,4695,7716,1494,1015,1772,5913,1127,1952,1950,8905,4064,9890,385,9357,7945,5035,7082,5369,4093,6546,5187,5637,2041,8946,1758,7111,6566,1027,1049,5148,7224,7248,296,6169,375,1656,7993,2816,3717,4279,4675,1609,3317,42,6201,3100,3144,163,9530,4531],
+ [7096,6070,1009,4988,3538,5801,7149,3063,2324,2912,7911,7002,4338,7880,2481,7368,3516,2016,7556,2193,1388,3865,8125,4637,4096,8114,750,3144,1938,7002,9343,4095,1392,4220,3455,6969,9647,1321,9048,1996,1640,6626,1788,314,9578,6630,2813,6626,4981,9908,7024,4355,3201,3521,3864,3303,464,1923,595,9801,3391,8366,8084,9374,1041,8807,9085,1892,9431,8317,9016,9221,8574,9981,9240,5395,2009,6310,2854,9255],
+ [8830,3145,2960,9615,8220,6061,3452,2918,6481,9278,2297,3385,6565,7066,7316,5682,107,7646,4466,68,1952,9603,8615,54,7191,791,6833,2560,693,9733,4168,570,9127,9537,1925,8287,5508,4297,8452,8795,6213,7994,2420,4208,524,5915,8602,8330,2651,8547,6156,1812,6271,7991,9407,9804,1553,6866,1128,2119,4691,9711,8315,5879,9935,6900,482,682,4126,1041,428,6247,3720,5882,7526,2582,4327,7725,3503,2631],
+ [2738,9323,721,7434,1453,6294,2957,3786,5722,6019,8685,4386,3066,9057,6860,499,5315,3045,5194,7111,3137,9104,941,586,3066,755,4177,8819,7040,5309,3583,3897,4428,7788,4721,7249,6559,7324,825,7311,3760,6064,6070,9672,4882,584,1365,9739,9331,5783,2624,7889,1604,1303,1555,7125,8312,425,8936,3233,7724,1480,403,7440,1784,1754,4721,1569,652,3893,4574,5692,9730,4813,9844,8291,9199,7101,3391,8914],
+ [6044,2928,9332,3328,8588,447,3830,1176,3523,2705,8365,6136,5442,9049,5526,8575,8869,9031,7280,706,2794,8814,5767,4241,7696,78,6570,556,5083,1426,4502,3336,9518,2292,1885,3740,3153,9348,9331,8051,2759,5407,9028,7840,9255,831,515,2612,9747,7435,8964,4971,2048,4900,5967,8271,1719,9670,2810,6777,1594,6367,6259,8316,3815,1689,6840,9437,4361,822,9619,3065,83,6344,7486,8657,8228,9635,6932,4864],
+ [8478,4777,6334,4678,7476,4963,6735,3096,5860,1405,5127,7269,7793,4738,227,9168,2996,8928,765,733,1276,7677,6258,1528,9558,3329,302,8901,1422,8277,6340,645,9125,8869,5952,141,8141,1816,9635,4025,4184,3093,83,2344,2747,9352,7966,1206,1126,1826,218,7939,2957,2729,810,8752,5247,4174,4038,8884,7899,9567,301,5265,5752,7524,4381,1669,3106,8270,6228,6373,754,2547,4240,2313,5514,3022,1040,9738],
+ [2265,8192,1763,1369,8469,8789,4836,52,1212,6690,5257,8918,6723,6319,378,4039,2421,8555,8184,9577,1432,7139,8078,5452,9628,7579,4161,7490,5159,8559,1011,81,478,5840,1964,1334,6875,8670,9900,739,1514,8692,522,9316,6955,1345,8132,2277,3193,9773,3923,4177,2183,1236,6747,6575,4874,6003,6409,8187,745,8776,9440,7543,9825,2582,7381,8147,7236,5185,7564,6125,218,7991,6394,391,7659,7456,5128,5294],
+ [2132,8992,8160,5782,4420,3371,3798,5054,552,5631,7546,4716,1332,6486,7892,7441,4370,6231,4579,2121,8615,1145,9391,1524,1385,2400,9437,2454,7896,7467,2928,8400,3299,4025,7458,4703,7206,6358,792,6200,725,4275,4136,7390,5984,4502,7929,5085,8176,4600,119,3568,76,9363,6943,2248,9077,9731,6213,5817,6729,4190,3092,6910,759,2682,8380,1254,9604,3011,9291,5329,9453,9746,2739,6522,3765,5634,1113,5789],
+ [5304,5499,564,2801,679,2653,1783,3608,7359,7797,3284,796,3222,437,7185,6135,8571,2778,7488,5746,678,6140,861,7750,803,9859,9918,2425,3734,2698,9005,4864,9818,6743,2475,132,9486,3825,5472,919,292,4411,7213,7699,6435,9019,6769,1388,802,2124,1345,8493,9487,8558,7061,8777,8833,2427,2238,5409,4957,8503,3171,7622,5779,6145,2417,5873,5563,5693,9574,9491,1937,7384,4563,6842,5432,2751,3406,7981]
+];
+```
+
+## --seed-contents--
+
+```js
+function pathSumFourWays(matrix) {
+
+ return true;
+}
+
+// Only change code above this line
+
+const testMatrix1 = [
+ [131, 673, 234, 103, 18],
+ [201, 96, 342, 965, 150],
+ [630, 803, 746, 422, 111],
+ [537, 699, 497, 121, 956],
+ [805, 732, 524, 37, 331]
+];
+
+pathSumFourWays(testMatrix1);
+```
+
+# --solutions--
+
+```js
+function pathSumFourWays(matrix) {
+ const MOVES = [
+ [-1, 0],
+ [1, 0],
+ [0, -1],
+ [0, 1]
+ ];
+
+ function getAllowedMoves(row, col) {
+ const moves = [];
+ for (let i = 0; i < MOVES.length; i++) {
+ const [rowChange, colChange] = MOVES[i];
+ const nextRow = row + rowChange;
+ const nextCol = col + colChange;
+ if (isMoveAllowed(nextRow, nextCol)) {
+ moves.push([nextRow, nextCol]);
+ }
+ }
+ return moves;
+ }
+
+ function isMoveAllowed(nextRow, nextCol) {
+ if (nextRow < 0 || nextRow >= size || nextCol < 0 || nextCol >= size) {
+ return false;
+ }
+ return true;
+ }
+
+ const size = matrix.length;
+ const resultMatrix = new Array(size)
+ .fill()
+ .map(() => new Array(size).fill(Infinity));
+
+ const [startRow, startCol] = new Array(2).fill(size - 1);
+ const queue = [[startRow, startCol]];
+ resultMatrix[startRow][startCol] = matrix[startRow][startCol];
+
+ while (queue.length > 0) {
+ const [curRow, curCol] = queue.shift();
+
+ const allowedMoves = getAllowedMoves(curRow, curCol);
+
+ for (let i = 0; i < allowedMoves.length; i++) {
+ const [nextRow, nextCol] = allowedMoves[i];
+ const bestPath = resultMatrix[nextRow][nextCol];
+ const newPath = resultMatrix[curRow][curCol] + matrix[nextRow][nextCol];
+ if (newPath < bestPath) {
+ resultMatrix[nextRow][nextCol] = newPath;
+ queue.push(allowedMoves[i]);
+ }
+ }
+ }
+ return resultMatrix[0][0];
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-84-monopoly-odds.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-84-monopoly-odds.md
new file mode 100644
index 00000000000..92c630f9429
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-84-monopoly-odds.md
@@ -0,0 +1,268 @@
+---
+id: 5900f3c11000cf542c50fed3
+title: 'Problem 84: Monopoly odds'
+challengeType: 1
+forumTopicId: 302198
+dashedName: problem-84-monopoly-odds
+---
+
+# --description--
+
+In the game, *Monopoly*, the standard board is set up in the following way:
+
+
+
+
+
+
| GO | +A1 | +CC1 | +A2 | +T1 | +R1 | +B1 | +CH1 | +B2 | +B3 | +JAIL | +
| H2 | ++ | C1 | +||||||||
| T2 | ++ | U1 | +||||||||
| H1 | ++ | C2 | +||||||||
| CH3 | ++ | C3 | +||||||||
| R4 | ++ | R2 | +||||||||
| G3 | ++ | D1 | +||||||||
| CC3 | ++ | CC2 | +||||||||
| G2 | ++ | D2 | +||||||||
| G1 | ++ | D3 | +||||||||
| G2J | +F3 | +U2 | +F2 | +F1 | +R3 | +E3 | +E2 | +CH2 | +E1 | +FP | +
+ +A player starts on the GO square and adds the scores on two 6-sided dice to determine the number of squares they advance in a clockwise direction. Without any further rules we would expect to visit each square with equal probability: 2.5%. However, landing on G2J (Go To Jail), CC (community chest), and CH (chance) changes this distribution. + +In addition to G2J, and one card from each of CC and CH, that orders the player to go directly to jail, if a player rolls three consecutive doubles, they do not advance the result of their 3rd roll. Instead they proceed directly to jail. + +At the beginning of the game, the CC and CH cards are shuffled. When a player lands on CC or CH they take a card from the top of the respective pile and, after following the instructions, it is returned to the bottom of the pile. There are sixteen cards in each pile, but for the purpose of this problem we are only concerned with cards that order a movement; any instruction not concerned with movement will be ignored and the player will remain on the CC/CH square. + +
-
+
- Community Chest (2/16 cards): +
- Advance to GO +
- Go to JAIL +
- Chance (10/16 cards): +
- Advance to GO +
- Go to JAIL +
- Go to C1 +
- Go to E3 +
- Go to H2 +
- Go to R1 +
- Go to next R (railway company) +
- Go to next R +
- Go to next U (utility company) +
- Go back 3 squares. +
-
+
-
+
+
+Although there may not exists a rectangular grid that contains exactly `n` rectangles, find the area of the grid with the nearest solution.
+
+# --hints--
+
+`countingRectangles(18)` should return a number.
+
+```js
+assert(typeof countingRectangles(18) === 'number');
+```
+
+`countingRectangles(18)` should return `6`.
+
+```js
+assert.strictEqual(countingRectangles(18), 6);
+```
+
+`countingRectangles(250)` should return `22`.
+
+```js
+assert.strictEqual(countingRectangles(250), 22);
+```
+
+`countingRectangles(50000)` should return `364`.
+
+```js
+assert.strictEqual(countingRectangles(50000), 364);
+```
+
+`countingRectangles(1000000)` should return `1632`.
+
+```js
+assert.strictEqual(countingRectangles(1000000), 1632);
+```
+
+`countingRectangles(2000000)` should return `2772`.
+
+```js
+assert.strictEqual(countingRectangles(2000000), 2772);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function countingRectangles(n) {
+
+ return true;
+}
+
+countingRectangles(18);
+```
+
+# --solutions--
+
+```js
+function countingRectangles(n) {
+ function numberOfRectangles(h, w) {
+ return (h * (h + 1) * w * (w + 1)) / 4;
+ }
+
+ function rectangleArea(h, w) {
+ return h * w;
+ }
+
+ let rectanglesCount = 1;
+ let maxSide = 1;
+ while (rectanglesCount < n) {
+ maxSide++;
+ rectanglesCount = numberOfRectangles(maxSide, 1);
+ }
+
+ let bestDiff = Math.abs(rectanglesCount - n);
+ let bestSize = [maxSide, 1];
+
+ let curHeight = maxSide - 1;
+ let curWidth = 1;
+
+ for (curWidth; curWidth < curHeight; curWidth++) {
+ for (curHeight; curHeight > curWidth; curHeight--) {
+ rectanglesCount = numberOfRectangles(curHeight, curWidth);
+ const curDiff = Math.abs(rectanglesCount - n);
+ if (curDiff < bestDiff) {
+ bestDiff = curDiff;
+ bestSize = [curHeight, curWidth];
+ }
+
+ if (rectanglesCount < n) {
+ break;
+ }
+ }
+ }
+ return rectangleArea(...bestSize);
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-86-cuboid-route.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-86-cuboid-route.md
new file mode 100644
index 00000000000..39a860bd794
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-86-cuboid-route.md
@@ -0,0 +1,94 @@
+---
+id: 5900f3c31000cf542c50fed5
+title: 'Problem 86: Cuboid route'
+challengeType: 1
+forumTopicId: 302200
+dashedName: problem-86-cuboid-route
+---
+
+# --description--
+
+A spider, S, sits in one corner of a cuboid room, measuring 6 by 5 by 3, and a fly, F, sits in the opposite corner. By travelling on the surfaces of the room the shortest "straight line" distance from S to F is 10 and the path is shown on the diagram.
+
+
+
+However, there are up to three "shortest" path candidates for any given cuboid and the shortest route doesn't always have integer length.
+
+It can be shown that there are exactly `2060` distinct cuboids, ignoring rotations, with integer dimensions, up to a maximum size of M by M by M, for which the shortest route has integer length when M = 100. This is the least value of M for which the number of solutions first exceeds two thousand; the number of solutions when M = 99 is `1975`.
+
+Find the least value of M such that the number of solutions first exceeds `n`.
+
+# --hints--
+
+`cuboidRoute(2000)` should return a number.
+
+```js
+assert(typeof cuboidRoute(2000) === 'number');
+```
+
+`cuboidRoute(2000)` should return `100`.
+
+```js
+assert.strictEqual(cuboidRoute(2000), 100);
+```
+
+`cuboidRoute(25000)` should return `320`.
+
+```js
+assert.strictEqual(cuboidRoute(25000), 320);
+```
+
+`cuboidRoute(500000)` should return `1309`.
+
+```js
+assert.strictEqual(cuboidRoute(500000), 1309);
+```
+
+`cuboidRoute(1000000)` should return `1818`.
+
+```js
+assert.strictEqual(cuboidRoute(1000000), 1818);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function cuboidRoute(n) {
+
+ return true;
+}
+
+cuboidRoute(2000);
+```
+
+# --solutions--
+
+```js
+function cuboidRoute(n) {
+ // Based on https://www.mathblog.dk/project-euler-86-shortest-path-cuboid/
+ function getLength(a, b) {
+ return Math.sqrt(a ** 2 + b ** 2);
+ }
+
+ let M = 2;
+ let counter = 0;
+
+ while (counter < n) {
+ M++;
+ for (let baseHeightWidth = 3; baseHeightWidth <= 2 * M; baseHeightWidth++) {
+ const pathLength = getLength(M, baseHeightWidth);
+ if (Number.isInteger(pathLength)) {
+ if (baseHeightWidth <= M) {
+ counter += Math.floor(baseHeightWidth / 2);
+ } else {
+ counter += 1 + M - Math.floor((baseHeightWidth + 1) / 2);
+ }
+ }
+ }
+ }
+
+ return M;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-87-prime-power-triples.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-87-prime-power-triples.md
new file mode 100644
index 00000000000..a6c51eff68d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-87-prime-power-triples.md
@@ -0,0 +1,131 @@
+---
+id: 5900f3c51000cf542c50fed8
+title: 'Problem 87: Prime power triples'
+challengeType: 1
+forumTopicId: 302201
+dashedName: problem-87-prime-power-triples
+---
+
+# --description--
+
+The smallest number expressible as the sum of a prime square, prime cube, and prime fourth power is `28`. In fact, there are exactly four numbers below fifty that can be expressed in such a way:
+
+
+ 28 = 22 + 23 + 24
+ 33 = 32 + 23 + 24
+ 49 = 52 + 23 + 24
+ 47 = 22 + 33 + 24 +
+ 33 = 32 + 23 + 24
+ 49 = 52 + 23 + 24
+ 47 = 22 + 33 + 24 +
+ +How many numbers below `n` can be expressed as the sum of a prime square, prime cube, and prime fourth power? + +# --hints-- + +`primePowerTriples(50)` should return a number. + +```js +assert(typeof primePowerTriples(50) === 'number'); +``` + +`primePowerTriples(50)` should return `4`. + +```js +assert.strictEqual(primePowerTriples(50), 4); +``` + +`primePowerTriples(10035)` should return `684`. + +```js +assert.strictEqual(primePowerTriples(10035), 684); +``` + +`primePowerTriples(500000)` should return `18899`. + +```js +assert.strictEqual(primePowerTriples(500000), 18899); +``` + +`primePowerTriples(5000000)` should return `138932`. + +```js +assert.strictEqual(primePowerTriples(5000000), 138932); +``` + +`primePowerTriples(50000000)` should return `1097343`. + +```js +assert.strictEqual(primePowerTriples(50000000), 1097343); +``` + +# --seed-- + +## --seed-contents-- + +```js +function primePowerTriples(n) { + + return true; +} + +primePowerTriples(50); +``` + +# --solutions-- + +```js +function primePowerTriples(n) { + function getSievePrimes(max) { + const primes = []; + const primesMap = new Array(max).fill(true); + primesMap[0] = false; + primesMap[1] = false; + + for (let i = 2; i <= max; i += 2) { + if (primesMap[i]) { + primes.push(i); + for (let j = i * i; j <= max; j = j + i) { + primesMap[j] = false; + } + } + if (i === 2) { + i = 1; + } + } + return primes; + } + + function getPowersSummed(numbers, powers, limit, curSum) { + if (curSum >= limit) { + return []; + } else if (powers.length === 0) { + return [curSum]; + } + + const powersSummed = []; + + const curPower = powers[0]; + const powersLeft = powers.slice(1); + for (let i = 0; i < numbers.length; i++) { + const curNumber = numbers[i]; + const nextSum = curSum + curNumber ** curPower; + if (nextSum >= limit) { + return powersSummed; + } + const result = getPowersSummed( + numbers, + powersLeft, + limit, + curSum + curNumber ** curPower + ); + powersSummed.push(...result); + } + return powersSummed; + } + + const maximumBaseNumber = Math.floor(Math.sqrt(n - 2 ** 3 - 2 ** 4)) + 1; + const primes = getSievePrimes(maximumBaseNumber); + const uniqueSums = new Set(getPowersSummed(primes, [2, 3, 4], n, 0)); + + return uniqueSums.size; +} +``` diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-88-product-sum-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-88-product-sum-numbers.md new file mode 100644 index 00000000000..46779896396 --- /dev/null +++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-88-product-sum-numbers.md @@ -0,0 +1,110 @@ +--- +id: 5900f3c51000cf542c50fed6 +title: 'Problem 88: Product-sum numbers' +challengeType: 1 +forumTopicId: 302203 +dashedName: problem-88-product-sum-numbers +--- + +# --description-- + +A natural number, `N`, that can be written as the sum and product of a given set of at least two natural numbers, $\\{a_1, a_2, \ldots , a_k\\}$ is called a product-sum number: $N = a_1 + a_2 + \cdots + a_k = a_1 × a_2 × \cdots × a_k$. + +For example, 6 = 1 + 2 + 3 = 1 × 2 × 3. + +For a given set of size, `k`, we shall call the smallest N with this property a minimal product-sum number. The minimal product-sum numbers for sets of size, `k` = 2, 3, 4, 5, and 6 are as follows. + +
+ k=2: 4 = 2 × 2 = 2 + 2
+ k=3: 6 = 1 × 2 × 3 = 1 + 2 + 3
+ k=4: 8 = 1 × 1 × 2 × 4 = 1 + 1 + 2 + 4
+ k=5: 8 = 1 × 1 × 2 × 2 × 2 = 1 + 1 + 2 + 2 + 2
+ k=6: 12 = 1 × 1 × 1 × 1 × 2 × 6 = 1 + 1 + 1 + 1 + 2 + 6 +
+ k=3: 6 = 1 × 2 × 3 = 1 + 2 + 3
+ k=4: 8 = 1 × 1 × 2 × 4 = 1 + 1 + 2 + 4
+ k=5: 8 = 1 × 1 × 2 × 2 × 2 = 1 + 1 + 2 + 2 + 2
+ k=6: 12 = 1 × 1 × 1 × 1 × 2 × 6 = 1 + 1 + 1 + 1 + 2 + 6 +
+ +Hence for 2 ≤ `k` ≤ 6, the sum of all the minimal product-sum numbers is 4 + 6 + 8 + 12 = 30; note that `8` is only counted once in the sum. + +In fact, as the complete set of minimal product-sum numbers for 2 ≤ `k` ≤ 12 is $\\{4, 6, 8, 12, 15, 16\\}$, the sum is `61`. + +What is the sum of all the minimal product-sum numbers for 2 ≤ `k` ≤ `limit`? + +# --hints-- + +`productSumNumbers(6)` should return a number. + +```js +assert(typeof productSumNumbers(6) === 'number'); +``` + +`productSumNumbers(6)` should return `30`. + +```js +assert.strictEqual(productSumNumbers(6), 30); +``` + +`productSumNumbers(12)` should return `61`. + +```js +assert.strictEqual(productSumNumbers(12), 61); +``` + +`productSumNumbers(300)` should return `12686`. + +```js +assert.strictEqual(productSumNumbers(300), 12686); +``` + +`productSumNumbers(6000)` should return `2125990`. + +```js +assert.strictEqual(productSumNumbers(6000), 2125990); +``` + +`productSumNumbers(12000)` should return `7587457`. + +```js +assert.strictEqual(productSumNumbers(12000), 7587457); +``` + +# --seed-- + +## --seed-contents-- + +```js +function productSumNumbers(limit) { + + return true; +} + +productSumNumbers(6); +``` + +# --solutions-- + +```js +function productSumNumbers(limit) { + function getProductSums(curProduct, curSum, factorsCount, start) { + const k = curProduct - curSum + factorsCount; + if (k <= limit) { + if (curProduct < minimalProductSums[k]) { + minimalProductSums[k] = curProduct; + } + for (let i = start; i < Math.floor((limit / curProduct) * 2) + 1; i++) { + getProductSums(curProduct * i, curSum + i, factorsCount + 1, i); + } + } + } + + const minimalProductSums = new Array(limit + 1).fill(2 * limit); + getProductSums(1, 1, 1, 2); + + const uniqueProductSums = [...new Set(minimalProductSums.slice(2))]; + + let sum = 0; + for (let i = 0; i < uniqueProductSums.length; i++) { + sum += uniqueProductSums[i]; + } + + return sum; +} +``` diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-89-roman-numerals.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-89-roman-numerals.md new file mode 100644 index 00000000000..52c03847a6b --- /dev/null +++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-89-roman-numerals.md @@ -0,0 +1,117 @@ +--- +id: 5900f3c51000cf542c50fed7 +title: 'Problem 89: Roman numerals' +challengeType: 1 +forumTopicId: 302204 +dashedName: problem-89-roman-numerals +--- + +# --description-- + +For a number written in Roman numerals to be considered valid there are basic rules which must be followed. Even though the rules allow some numbers to be expressed in more than one way there is always a *best* way of writing a particular number. + +- Numerals must be arranged in descending order of size. +- M, C, and X cannot be equaled or exceeded by smaller denominations. +- D, L, and V can each only appear once. + +In addition to the three rules given above, if subtractive combinations are used then the following four rules must be followed. + +- Only one I, X, and C can be used as the leading numeral in part of a subtractive pair. +- I can only be placed before V and X. +- X can only be placed before L and C. +- C can only be placed before D and M. + +For example, it would appear that there are at least six ways of writing the number sixteen: + +
+ IIIIIIIIIIIIIIII
+ VIIIIIIIIIII
+ VVIIIIII
+ XIIIIII
+ VVVI
+ XVI
+
+
+However, according to the rules only XIIIIII and XVI are valid, and the last example is considered to be the most efficient, as it uses the least number of numerals.
+
+The array, `roman`, will contain numbers written with valid, but not necessarily minimal, Roman numerals.
+
+Find the number of characters saved by writing each of these in their minimal form.
+
+**Note:** You can assume that all the Roman numerals in the array contain no more than four consecutive identical units.
+
+# --hints--
+
+`romanNumerals(testNumerals1)` should return a number.
+
+```js
+assert(typeof romanNumerals(_testNumerals1) === 'number');
+```
+
+`romanNumerals(testNumerals1)` should return `19`.
+
+```js
+assert.strictEqual(romanNumerals(_testNumerals1), 19);
+```
+
+`romanNumerals(testNumerals2)` should return `743`.
+
+```js
+assert.strictEqual(romanNumerals(_testNumerals2), 743);
+```
+
+# --seed--
+
+## --after-user-code--
+
+```js
+const _testNumerals1 = [
+ 'XIIIIII', 'XVI', 'MMMCCLXVIIII', 'XXXXVI', 'MMMMXX', 'CCLI', 'CCCCXX', 'MMMMDCXXXXI', 'DCCCCIIII', 'MXVIIII'
+];
+const _testNumerals2 = [
+ 'MMMMDCLXXII','MMDCCCLXXXIII','MMMDLXVIIII','MMMMDXCV','DCCCLXXII','MMCCCVI','MMMCDLXXXVII','MMMMCCXXI','MMMCCXX','MMMMDCCCLXXIII','MMMCCXXXVII','MMCCCLXXXXIX','MDCCCXXIIII','MMCXCVI','CCXCVIII','MMMCCCXXXII','MDCCXXX','MMMDCCCL','MMMMCCLXXXVI','MMDCCCXCVI','MMMDCII','MMMCCXII','MMMMDCCCCI','MMDCCCXCII','MDCXX','CMLXXXVII','MMMXXI','MMMMCCCXIV','MLXXII','MCCLXXVIIII','MMMMCCXXXXI','MMDCCCLXXII','MMMMXXXI','MMMDCCLXXX','MMDCCCLXXIX','MMMMLXXXV','MCXXI','MDCCCXXXVII','MMCCCLXVII','MCDXXXV','CCXXXIII','CMXX','MMMCLXIV','MCCCLXXXVI','DCCCXCVIII','MMMDCCCCXXXIV','CDXVIIII','MMCCXXXV','MDCCCXXXII','MMMMD','MMDCCLXIX','MMMMCCCLXXXXVI','MMDCCXLII','MMMDCCCVIIII','DCCLXXXIIII','MDCCCCXXXII','MMCXXVII','DCCCXXX','CCLXIX','MMMXI','MMMMCMLXXXXVIII','MMMMDLXXXVII','MMMMDCCCLX','MMCCLIV','CMIX','MMDCCCLXXXIIII','CLXXXII','MMCCCCXXXXV','MMMMDLXXXVIIII','MMMDCCCXXI','MMDCCCCLXXVI','MCCCCLXX','MMCDLVIIII','MMMDCCCLIX','MMMMCCCCXIX','MMMDCCCLXXV','XXXI','CDLXXXIII','MMMCXV','MMDCCLXIII','MMDXXX','MMMMCCCLVII','MMMDCI','MMMMCDLXXXIIII','MMMMCCCXVI','CCCLXXXVIII','MMMMCML','MMMMXXIV','MMMCCCCXXX','DCCX','MMMCCLX','MMDXXXIII','CCCLXIII','MMDCCXIII','MMMCCCXLIV','CLXXXXI','CXVI','MMMMCXXXIII','CLXX','DCCCXVIII','MLXVII','DLXXXX','MMDXXI','MMMMDLXXXXVIII','MXXII','LXI','DCCCCXLIII','MMMMDV','MMMMXXXIV','MDCCCLVIII','MMMCCLXXII','MMMMDCCXXXVI','MMMMLXXXIX','MDCCCLXXXI','MMMMDCCCXV','MMMMCCCCXI','MMMMCCCLIII','MDCCCLXXI','MMCCCCXI','MLXV','MMCDLXII','MMMMDXXXXII','MMMMDCCCXL','MMMMCMLVI','CCLXXXIV','MMMDCCLXXXVI','MMCLII','MMMCCCCXV','MMLXXXIII','MMMV','MMMV','DCCLXII','MMDCCCCXVI','MMDCXLVIII','CCLIIII','CCCXXV','MMDCCLXXXVIIII','MMMMDCLXXVIII','MMMMDCCCXCI','MMMMCCCXX','MMCCXLV','MMMDCCCLXIX','MMCCLXIIII','MMMDCCCXLIX','MMMMCCCLXIX','CMLXXXXI','MCMLXXXIX','MMCDLXI','MMDCLXXVIII','MMMMDCCLXI','MCDXXV','DL','CCCLXXII','MXVIIII','MCCCCLXVIII','CIII','MMMDCCLXXIIII','MMMDVIII','MMMMCCCLXXXXVII','MMDXXVII','MMDCCLXXXXV','MMMMCXLVI','MMMDCCLXXXII','MMMDXXXVI','MCXXII','CLI','DCLXXXIX','MMMCLI','MDCLXIII','MMMMDCCXCVII','MMCCCLXXXV','MMMDCXXVIII','MMMCDLX','MMMCMLII','MMMIV','MMMMDCCCLVIII','MMMDLXXXVIII','MCXXIV','MMMMLXXVI','CLXXIX','MMMCCCCXXVIIII','DCCLXXXV','MMMDCCCVI','LI','CLXXXVI','MMMMCCCLXXVI','MCCCLXVI','CCXXXIX','MMDXXXXI','MMDCCCXLI','DCCCLXXXVIII','MMMMDCCCIV','MDCCCCXV','MMCMVI','MMMMCMLXXXXV','MMDCCLVI','MMMMCCXLVIII','DCCCCIIII','MMCCCCIII','MMMDCCLXXXVIIII','MDCCCLXXXXV','DVII','MMMV','DCXXV','MMDCCCXCV','DCVIII','MMCDLXVI','MCXXVIII','MDCCXCVIII','MMDCLX','MMMDCCLXIV','MMCDLXXVII','MMDLXXXIIII','MMMMCCCXXII','MMMDCCCXLIIII','DCCCCLXVII','MMMCLXXXXIII','MCCXV','MMMMDCXI','MMMMDCLXXXXV','MMMCCCLII','MMCMIX','MMDCCXXV','MMDLXXXVI','MMMMDCXXVIIII','DCCCCXXXVIIII','MMCCXXXIIII','MMDCCLXXVIII','MDCCLXVIIII','MMCCLXXXV','MMMMDCCCLXXXVIII','MMCMXCI','MDXLII','MMMMDCCXIV','MMMMLI','DXXXXIII','MMDCCXI','MMMMCCLXXXIII','MMMDCCCLXXIII','MDCLVII','MMCD','MCCCXXVII','MMMMDCCIIII','MMMDCCXLVI','MMMCLXXXVII','MMMCCVIIII','MCCCCLXXIX','DL','DCCCLXXVI','MMDXCI','MMMMDCCCCXXXVI','MMCII','MMMDCCCXXXXV','MMMCDXLV','MMDCXXXXIV','MMD','MDCCCLXXXX','MMDCXLIII','MMCCXXXII','MMDCXXXXVIIII','DCCCLXXI','MDXCVIIII','MMMMCCLXXVIII','MDCLVIIII','MMMCCCLXXXIX','MDCLXXXV','MDLVIII','MMMMCCVII','MMMMDCXIV','MMMCCCLXIIII','MMIIII','MMMMCCCLXXIII','CCIII','MMMCCLV','MMMDXIII','MMMCCCXC','MMMDCCCXXI','MMMMCCCCXXXII','CCCLVI','MMMCCCLXXXVI','MXVIIII','MMMCCCCXIIII','CLXVII','MMMCCLXX','CCCCLXIV','MMXXXXII','MMMMCCLXXXX','MXL','CCXVI','CCCCLVIIII','MMCCCII','MCCCLVIII','MMMMCCCX','MCDLXXXXIV','MDCCCXIII','MMDCCCXL','MMMMCCCXXIII','DXXXIV','CVI','MMMMDCLXXX','DCCCVII','MMCMLXIIII','MMMDCCCXXXIII','DCCC','MDIII','MMCCCLXVI','MMMCCCCLXXI','MMDCCCCXVIII','CCXXXVII','CCCXXV','MDCCCXII','MMMCMV','MMMMCMXV','MMMMDCXCI','DXXI','MMCCXLVIIII','MMMMCMLII','MDLXXX','MMDCLXVI','CXXI','MMMDCCCLIIII','MMMCXXI','MCCIII','MMDCXXXXI','CCXCII','MMMMDXXXV','MMMCCCLXV','MMMMDLXV','MMMCCCCXXXII','MMMCCCVIII','DCCCCLXXXXII','MMCLXIV','MMMMCXI','MLXXXXVII','MMMCDXXXVIII','MDXXII','MLV','MMMMDLXVI','MMMCXII','XXXIII','MMMMDCCCXXVI','MMMLXVIIII','MMMLX','MMMCDLXVII','MDCCCLVII','MMCXXXVII','MDCCCCXXX','MMDCCCLXIII','MMMMDCXLIX','MMMMCMXLVIII','DCCCLXXVIIII','MDCCCLIII','MMMCMLXI','MMMMCCLXI','MMDCCCLIII','MMMDCCCVI','MMDXXXXIX','MMCLXXXXV','MMDXXX','MMMXIII','DCLXXIX','DCCLXII','MMMMDCCLXVIII','MDCCXXXXIII','CCXXXII','MMMMDCXXV','MMMCCCXXVIII','MDCVIII','MMMCLXXXXIIII','CLXXXI','MDCCCCXXXIII','MMMMDCXXX','MMMDCXXIV','MMMCCXXXVII','MCCCXXXXIIII','CXVIII','MMDCCCCIV','MMMMCDLXXV','MMMDLXIV','MDXCIII','MCCLXXXI','MMMDCCCXXIV','MCXLIII','MMMDCCCI','MCCLXXX','CCXV','MMDCCLXXI','MMDLXXXIII','MMMMDCXVII','MMMCMLXV','MCLXVIII','MMMMCCLXXVI','MMMDCCLXVIIII','MMMMDCCCIX','DLXXXXIX','DCCCXXII','MMMMIII','MMMMCCCLXXVI','DCCCXCIII','DXXXI','MXXXIIII','CCXII','MMMDCCLXXXIIII','MMMCXX','MMMCMXXVII','DCCCXXXX','MMCDXXXVIIII','MMMMDCCXVIII','LV','MMMDCCCCVI','MCCCII','MMCMLXVIIII','MDCCXI','MMMMDLXVII','MMCCCCLXI','MMDCCV','MMMCCCXXXIIII','MMMMDI','MMMDCCCXCV','MMDCCLXXXXI','MMMDXXVI','MMMDCCCLVI','MMDCXXX','MCCCVII','MMMMCCCLXII','MMMMXXV','MMCMXXV','MMLVI','MMDXXX','MMMMCVII','MDC','MCCIII','MMMMDCC','MMCCLXXV','MMDCCCXXXXVI','MMMMCCCLXV','CDXIIII','MLXIIII','CCV','MMMCMXXXI','CCCCLXVI','MDXXXII','MMMMCCCLVIII','MMV','MMMCLII','MCMLI','MMDCCXX','MMMMCCCCXXXVI','MCCLXXXI','MMMCMVI','DCCXXX','MMMMCCCLXV','DCCCXI','MMMMDCCCXIV','CCCXXI','MMDLXXV','CCCCLXXXX','MCCCLXXXXII','MMDCIX','DCCXLIIII','DXIV','MMMMCLII','CDLXI','MMMCXXVII','MMMMDCCCCLXIII','MMMDCLIIII','MCCCCXXXXII','MMCCCLX','CCCCLIII','MDCCLXXVI','MCMXXIII','MMMMDLXXVIII','MMDCCCCLX','MMMCCCLXXXX','MMMCDXXVI','MMMDLVIII','CCCLXI','MMMMDCXXII','MMDCCCXXI','MMDCCXIII','MMMMCLXXXVI','MDCCCCXXVI','MDV','MMDCCCCLXXVI','MMMMCCXXXVII','MMMDCCLXXVIIII','MMMCCCCLXVII','DCCXLI','MMCLXXXVIII','MCCXXXVI','MMDCXLVIII','MMMMCXXXII','MMMMDCCLXVI','MMMMCMLI','MMMMCLXV','MMMMDCCCXCIV','MCCLXXVII','LXXVIIII','DCCLII','MMMCCCXCVI','MMMCLV','MMDCCCXXXXVIII','DCCCXV','MXC','MMDCCLXXXXVII','MMMMCML','MMDCCCLXXVIII','DXXI','MCCCXLI','DCLXXXXI','MMCCCLXXXXVIII','MDCCCCLXXVIII','MMMMDXXV','MMMDCXXXVI','MMMCMXCVII','MMXVIIII','MMMDCCLXXIV','MMMCXXV','DXXXVIII','MMMMCLXVI','MDXII','MMCCCLXX','CCLXXI','DXIV','MMMCLIII','DLII','MMMCCCXLIX','MMCCCCXXVI','MMDCXLIII','MXXXXII','CCCLXXXV','MDCLXXVI','MDCXII','MMMCCCLXXXIII','MMDCCCCLXXXII','MMMMCCCLXXXV','MMDCXXI','DCCCXXX','MMMDCCCCLII','MMMDCCXXII','MMMMCDXCVIII','MMMCCLXVIIII','MMXXV','MMMMCDXIX','MMMMCCCX','MMMCCCCLXVI','MMMMDCLXXVIIII','MMMMDCXXXXIV','MMMCMXII','MMMMXXXIII','MMMMDLXXXII','DCCCLIV','MDXVIIII','MMMCLXXXXV','CCCCXX','MMDIX','MMCMLXXXVIII','DCCXLIII','DCCLX','D','MCCCVII','MMMMCCCLXXXIII','MDCCCLXXIIII','MMMDCCCCLXXXVII','MMMMCCCVII','MMMDCCLXXXXVI','CDXXXIV','MCCLXVIII','MMMMDLX','MMMMDXII','MMMMCCCCLIIII','MCMLXXXXIII','MMMMDCCCIII','MMDCLXXXIII','MDCCCXXXXIV','XXXXVII','MMMDCCCXXXII','MMMDCCCXLII','MCXXXV','MDCXXVIIII','MMMCXXXXIIII','MMMMCDXVII','MMMDXXIII','MMMMCCCCLXI','DCLXXXXVIIII','LXXXXI','CXXXIII','MCDX','MCCLVII','MDCXXXXII','MMMCXXIV','MMMMLXXXX','MMDCCCCXLV','MLXXX','MMDCCCCLX','MCDLIII','MMMCCCLXVII','MMMMCCCLXXIV','MMMDCVIII','DCCCCXXIII','MMXCI','MMDCCIV','MMMMDCCCXXXIV','CCCLXXI','MCCLXXXII','MCMIII','CCXXXI','DCCXXXVIII','MMMMDCCXLVIIII','MMMMCMXXXV','DCCCLXXV','DCCXCI','MMMMDVII','MMMMDCCCLXVIIII','CCCXCV','MMMMDCCXX','MCCCCII','MMMCCCXC','MMMCCCII','MMDCCLXXVII','MMDCLIIII','CCXLIII','MMMDCXVIII','MMMCCCIX','MCXV','MMCCXXV','MLXXIIII','MDCCXXVI','MMMCCCXX','MMDLXX','MMCCCCVI','MMDCCXX','MMMMDCCCCXCV','MDCCCXXXII','MMMMDCCCCXXXX','XCIV','MMCCCCLX','MMXVII','MLXXI','MMMDXXVIII','MDCCCCII','MMMCMLVII','MMCLXXXXVIII','MDCCCCLV','MCCCCLXXIIII','MCCCLII','MCDXLVI','MMMMDXVIII','DCCLXXXIX','MMMDCCLXIV','MDCCCCXLIII','CLXXXXV','MMMMCCXXXVI','MMMDCCCXXI','MMMMCDLXXVII','MCDLIII','MMCCXLVI','DCCCLV','MCDLXX','DCLXXVIII','MMDCXXXIX','MMMMDCLX','MMDCCLI','MMCXXXV','MMMCCXII','MMMMCMLXII','MMMMCCV','MCCCCLXIX','MMMMCCIII','CLXVII','MCCCLXXXXIIII','MMMMDCVIII','MMDCCCLXI','MMLXXIX','CMLXIX','MMDCCCXLVIIII','DCLXII','MMMCCCXLVII','MDCCCXXXV','MMMMDCCXCVI','DCXXX','XXVI','MMLXIX','MMCXI','DCXXXVII','MMMMCCCXXXXVIII','MMMMDCLXI','MMMMDCLXXIIII','MMMMVIII','MMMMDCCCLXII','MDCXCI','MMCCCXXIIII','CCCCXXXXV','MMDCCCXXI','MCVI','MMDCCLXVIII','MMMMCXL','MLXVIII','CMXXVII','CCCLV','MDCCLXXXIX','MMMCCCCLXV','MMDCCLXII','MDLXVI','MMMCCCXVIII','MMMMCCLXXXI','MMCXXVII','MMDCCCLXVIII','MMMCXCII','MMMMDCLVIII','MMMMDCCCXXXXII','MMDCCCCLXXXXVI','MDCCXL','MDCCLVII','MMMMDCCCLXXXVI','DCCXXXIII','MMMMDCCCCLXXXV','MMCCXXXXVIII','MMMCCLXXVIII','MMMDCLXXVIII','DCCCI','MMMMLXXXXVIIII','MMMCCCCLXXII','MMCLXXXVII','CCLXVI','MCDXLIII','MMCXXVIII','MDXIV','CCCXCVIII','CLXXVIII','MMCXXXXVIIII','MMMDCLXXXIV','CMLVIII','MCDLIX','MMMMDCCCXXXII','MMMMDCXXXIIII','MDCXXI','MMMDCXLV','MCLXXVIII','MCDXXII','IV','MCDLXXXXIII','MMMMDCCLXV','CCLI','MMMMDCCCXXXVIII','DCLXII','MCCCLXVII','MMMMDCCCXXXVI','MMDCCXLI','MLXI','MMMCDLXVIII','MCCCCXCIII','XXXIII','MMMDCLXIII','MMMMDCL','DCCCXXXXIIII','MMDLVII','DXXXVII','MCCCCXXIIII','MCVII','MMMMDCCXL','MMMMCXXXXIIII','MCCCCXXIV','MMCLXVIII','MMXCIII','MDCCLXXX','MCCCLIIII','MMDCLXXI','MXI','MCMLIV','MMMCCIIII','DCCLXXXVIIII','MDCLIV','MMMDCXIX','CMLXXXI','DCCLXXXVII','XXV','MMMXXXVI','MDVIIII','CLXIII','MMMCDLVIIII','MMCCCCVII','MMMLXX','MXXXXII','MMMMCCCLXVIII','MMDCCCXXVIII','MMMMDCXXXXI','MMMMDCCCXXXXV','MMMXV','MMMMCCXVIIII','MMDCCXIIII','MMMXXVII','MDCCLVIIII','MMCXXIIII','MCCCLXXIV','DCLVIII','MMMLVII','MMMCXLV','MMXCVII','MMMCCCLXXXVII','MMMMCCXXII','DXII','MMMDLV','MCCCLXXVIII','MMMCLIIII','MMMMCLXXXX','MMMCLXXXIIII','MDCXXIII','MMMMCCXVI','MMMMDLXXXIII','MMMDXXXXIII','MMMMCCCCLV','MMMDLXXXI','MMMCCLXXVI','MMMMXX','MMMMDLVI','MCCCCLXXX','MMMXXII','MMXXII','MMDCCCCXXXI','MMMDXXV','MMMDCLXXXVIIII','MMMDLXXXXVII','MDLXIIII','CMXC','MMMXXXVIII','MDLXXXVIII','MCCCLXXVI','MMCDLIX','MMDCCCXVIII','MDCCCXXXXVI','MMMMCMIV','MMMMDCIIII','MMCCXXXV','XXXXVI','MMMMCCXVII','MMCCXXIV','MCMLVIIII','MLXXXIX','MMMMLXXXIX','CLXXXXIX','MMMDCCCCLVIII','MMMMCCLXXIII','MCCCC','DCCCLIX','MMMCCCLXXXII','MMMCCLXVIIII','MCLXXXV','CDLXXXVII','DCVI','MMX','MMCCXIII','MMMMDCXX','MMMMXXVIII','DCCCLXII','MMMMCCCXLIII','MMMMCLXV','DXCI','MMMMCLXXX','MMMDCCXXXXI','MMMMXXXXVI','DCLX','MMMCCCXI','MCCLXXX','MMCDLXXII','DCCLXXI','MMMCCCXXXVI','MCCCCLXXXVIIII','CDLVIII','DCCLVI','MMMMDCXXXVIII','MMCCCLXXXIII','MMMMDCCLXXV','MMMXXXVI','CCCLXXXXIX','CV','CCCCXIII','CCCCXVI','MDCCCLXXXIIII','MMDCCLXXXII','MMMMCCCCLXXXI','MXXV','MMCCCLXXVIIII','MMMCCXII','MMMMCCXXXIII','MMCCCLXXXVI','MMMDCCCLVIIII','MCCXXXVII','MDCLXXV','XXXV','MMDLI','MMMCCXXX','MMMMCXXXXV','CCCCLIX','MMMMDCCCLXXIII','MMCCCXVII','DCCCXVI','MMMCCCXXXXV','MDCCCCXCV','CLXXXI','MMMMDCCLXX','MMMDCCCIII','MMCLXXVII','MMMDCCXXIX','MMDCCCXCIIII','MMMCDXXIIII','MMMMXXVIII','MMMMDCCCCLXVIII','MDCCCXX','MMMMCDXXI','MMMMDLXXXIX','CCXVI','MDVIII','MMCCLXXI','MMMDCCCLXXI','MMMCCCLXXVI','MMCCLXI','MMMMDCCCXXXIV','DLXXXVI','MMMMDXXXII','MMMXXIIII','MMMMCDIV','MMMMCCCXLVIII','MMMMCXXXVIII','MMMCCCLXVI','MDCCXVIII','MMCXX','CCCLIX','MMMMDCCLXXII','MDCCCLXXV','MMMMDCCCXXIV','DCCCXXXXVIII','MMMDCCCCXXXVIIII','MMMMCCXXXV','MDCLXXXIII','MMCCLXXXIV','MCLXXXXIIII','DXXXXIII','MCCCXXXXVIII','MMCLXXIX','MMMMCCLXIV','MXXII','MMMCXIX','MDCXXXVII','MMDCCVI','MCLXXXXVIII','MMMCXVI','MCCCLX','MMMCDX','CCLXVIIII','MMMCCLX','MCXXVIII','LXXXII','MCCCCLXXXI','MMMI','MMMCCCLXIV','MMMCCCXXVIIII','CXXXVIII','MMCCCXX','MMMCCXXVIIII','MCCLXVI','MMMCCCCXXXXVI','MMDCCXCIX','MCMLXXI','MMCCLXVIII','CDLXXXXIII','MMMMDCCXXII','MMMMDCCLXXXVII','MMMDCCLIV','MMCCLXIII','MDXXXVII','DCCXXXIIII','MCII','MMMDCCCLXXI','MMMLXXIII','MDCCCLIII','MMXXXVIII','MDCCXVIIII','MDCCCCXXXVII','MMCCCXVI','MCMXXII','MMMCCCLVIII','MMMMDCCCXX','MCXXIII','MMMDLXI','MMMMDXXII','MDCCCX','MMDXCVIIII','MMMDCCCCVIII','MMMMDCCCCXXXXVI','MMDCCCXXXV','MMCXCIV','MCMLXXXXIII','MMMCCCLXXVI','MMMMDCLXXXV','CMLXIX','DCXCII','MMXXVIII','MMMMCCCXXX','XXXXVIIII'
+];
+```
+
+## --seed-contents--
+
+```js
+function romanNumerals(roman) {
+
+ return true;
+}
+
+// Only change code above this line
+
+const testNumerals1 = [
+ 'XIIIIII', 'XVI', 'MMMCCLXVIIII', 'XXXXVI', 'MMMMXX', 'CCLI', 'CCCCXX', 'MMMMDCXXXXI', 'DCCCCIIII', 'MXVIIII'
+];
+
+romanNumerals(testNumerals1);
+```
+
+# --solutions--
+
+```js
+function romanNumerals(roman) {
+ const numerals = [...roman];
+ const replaces = [
+ ['VIIII', 'IX'],
+ ['IIII', 'IV'],
+ ['LXXXX', 'XC'],
+ ['XXXX', 'XL'],
+ ['DCCCC', 'CM'],
+ ['CCCC', 'CD']
+ ];
+ let savedChars = 0;
+ for (let i = 0; i < numerals.length; i++) {
+ const charsBefore = numerals[i].length;
+ for (let j = 0; j < replaces.length; j++) {
+ numerals[i] = numerals[i].replace(...replaces[j]);
+ }
+ const charsAfter = numerals[i].length;
+ savedChars += charsBefore - charsAfter;
+ }
+ return savedChars;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-9-special-pythagorean-triplet.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-9-special-pythagorean-triplet.md
new file mode 100644
index 00000000000..a853dd4415e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-9-special-pythagorean-triplet.md
@@ -0,0 +1,74 @@
+---
+id: 5900f3761000cf542c50fe88
+title: 'Problem 9: Special Pythagorean triplet'
+challengeType: 1
+forumTopicId: 302205
+dashedName: problem-9-special-pythagorean-triplet
+---
+
+# --description--
+
+A Pythagorean triplet is a set of three natural numbers, `a` < `b` < `c`, for which,
+
++ VIIIIIIIIIII
+ VVIIIIII
+ XIIIIII
+ VVVI
+ XVI
+
a2 + b2 = c2
+
+For example, 32 + 42 = 9 + 16 = 25 = 52.
+
+There exists exactly one Pythagorean triplet for which `a` + `b` + `c` = 1000. Find the product `abc` such that `a` + `b` + `c` = `n`.
+
+# --hints--
+
+`specialPythagoreanTriplet(24)` should return a number.
+
+```js
+assert(typeof specialPythagoreanTriplet(24) === 'number');
+```
+
+`specialPythagoreanTriplet(24)` should return 480.
+
+```js
+assert.strictEqual(specialPythagoreanTriplet(24), 480);
+```
+
+`specialPythagoreanTriplet(120)` should return 49920, 55080 or 60000.
+
+```js
+assert([49920, 55080, 60000].includes(specialPythagoreanTriplet(120)));
+```
+
+`specialPythagoreanTriplet(1000)` should return 31875000.
+
+```js
+assert.strictEqual(specialPythagoreanTriplet(1000), 31875000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function specialPythagoreanTriplet(n) {
+ let sumOfabc = n;
+
+ return true;
+}
+
+specialPythagoreanTriplet(1000);
+```
+
+# --solutions--
+
+```js
+const specialPythagoreanTriplet = (n)=>{
+ let sumOfabc = n;
+ let a,b,c;
+ for(a = 1; a<=sumOfabc/3; a++){
+ for(b = a+1; b<=sumOfabc/2; b++){
+ c = Math.sqrt(a*a+b*b);
+ if((a+b+c) == sumOfabc){
+ return a*b*c;
+ }
+ }
+ }
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-90-cube-digit-pairs.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-90-cube-digit-pairs.md
new file mode 100644
index 00000000000..3e1206b4c4f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-90-cube-digit-pairs.md
@@ -0,0 +1,65 @@
+---
+id: 5900f3c61000cf542c50fed9
+title: 'Problem 90: Cube digit pairs'
+challengeType: 1
+forumTopicId: 302207
+dashedName: problem-90-cube-digit-pairs
+---
+
+# --description--
+
+Each of the six faces on a cube has a different digit (0 to 9) written on it; the same is done to a second cube. By placing the two cubes side-by-side in different positions we can form a variety of 2-digit numbers.
+
+For example, the square number 64 could be formed:
+
+
+
+In fact, by carefully choosing the digits on both cubes it is possible to display all of the square numbers below one-hundred: 01, 04, 09, 16, 25, 36, 49, 64, and 81.
+
+For example, one way this can be achieved is by placing {0, 5, 6, 7, 8, 9} on one cube and {1, 2, 3, 4, 8, 9} on the other cube.
+
+However, for this problem we shall allow the 6 or 9 to be turned upside-down so that an arrangement like {0, 5, 6, 7, 8, 9} and {1, 2, 3, 4, 6, 7} allows for all nine square numbers to be displayed; otherwise it would be impossible to obtain 09.
+
+In determining a distinct arrangement we are interested in the digits on each cube, not the order.
+
+
+ {1, 2, 3, 4, 5, 6} is equivalent to {3, 6, 4, 1, 2, 5}
+ {1, 2, 3, 4, 5, 6} is distinct from {1, 2, 3, 4, 5, 9} +
+
+But because we are allowing 6 and 9 to be reversed, the two distinct sets in the last example both represent the extended set {1, 2, 3, 4, 5, 6, 9} for the purpose of forming 2-digit numbers.
+
+How many distinct arrangements of the two cubes allow for all of the square numbers to be displayed?
+
+# --hints--
+
+`cubeDigitPairs()` should return a number.
+
+```js
+assert(typeof cubeDigitPairs() === 'number');
+```
+
+`cubeDigitPairs()` should return 1217.
+
+```js
+assert.strictEqual(cubeDigitPairs(), 1217);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function cubeDigitPairs() {
+
+ return true;
+}
+
+cubeDigitPairs();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-91-right-triangles-with-integer-coordinates.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-91-right-triangles-with-integer-coordinates.md
new file mode 100644
index 00000000000..7874cbab3fc
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-91-right-triangles-with-integer-coordinates.md
@@ -0,0 +1,119 @@
+---
+id: 5900f3c71000cf542c50feda
+title: 'Problem 91: Right triangles with integer coordinates'
+challengeType: 1
+forumTopicId: 302208
+dashedName: problem-91-right-triangles-with-integer-coordinates
+---
+
+# --description--
+
+The points ${P}(x_1, y_1)$ and ${Q}(x_2, y_2)$ are plotted at integer co-ordinates and are joined to the origin, ${O}(0, 0)$, to form ${\Delta}OPQ$.
+
++ {1, 2, 3, 4, 5, 6} is distinct from {1, 2, 3, 4, 5, 9} +
+
+There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is, $0 ≤ x_1, y_1, x_2, y_2 ≤ 2$.
+
+
+
+Given that $0 ≤ x_1, y_1, x_2, y_2 ≤ limit$, how many right triangles can be formed?
+
+# --hints--
+
+`rightTrianglesIntCoords(2)` should return a number.
+
+```js
+assert(typeof rightTrianglesIntCoords(2) === 'number');
+```
+
+`rightTrianglesIntCoords(2)` should return `14`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(2), 14);
+```
+
+`rightTrianglesIntCoords(10)` should return `448`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(10), 448);
+```
+
+`rightTrianglesIntCoords(25)` should return `3207`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(25), 3207);
+```
+
+`rightTrianglesIntCoords(50)` should return `14234`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(50), 14234);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function rightTrianglesIntCoords(limit) {
+
+ return true;
+}
+
+rightTrianglesIntCoords(2);
+```
+
+# --solutions--
+
+```js
+function rightTrianglesIntCoords(limit) {
+ function isRightTriangle(points) {
+ for (let i = 0; i < points.length; i++) {
+ const pointA = points[i];
+ const pointB = points[(i + 1) % 3];
+ const pointC = points[(i + 2) % 3];
+ const vectorAB = [pointB[0] - pointA[0], pointB[1] - pointA[1]];
+ const vectorAC = [pointC[0] - pointA[0], pointC[1] - pointA[1]];
+
+ if (isRightAngleBetween(vectorAB, vectorAC)) {
+ return true;
+ }
+ }
+ return false;
+ }
+
+ function isRightAngleBetween(vector1, vector2) {
+ return vector1[0] * vector2[0] + vector1[1] * vector2[1] === 0;
+ }
+
+ function getSetKey(points) {
+ return (
+ '0.0,' +
+ points
+ .sort((a, b) => a[0] - b[0])
+ .map(point => point.join('.'))
+ .join(',')
+ );
+ }
+
+ const pointO = [0, 0];
+ const rightTriangles = new Set();
+ for (let x1 = 1; x1 <= limit; x1++) {
+ for (let y1 = 0; y1 <= limit; y1++) {
+ const pointP = [x1, y1];
+ for (let x2 = 0; x2 <= limit; x2++) {
+ for (let y2 = 1; y2 <= limit; y2++) {
+ const pointQ = [x2, y2];
+ if (pointP[0] === pointQ[0] && pointP[1] === pointQ[1]) {
+ continue;
+ }
+ if (isRightTriangle([pointO, pointP, pointQ])) {
+ rightTriangles.add(getSetKey([pointP, pointQ]));
+ }
+ }
+ }
+ }
+ }
+ return rightTriangles.size;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-92-square-digit-chains.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-92-square-digit-chains.md
new file mode 100644
index 00000000000..c560f06847c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-92-square-digit-chains.md
@@ -0,0 +1,153 @@
+---
+id: 5900f3c81000cf542c50fedb
+title: 'Problem 92: Square digit chains'
+challengeType: 1
+forumTopicId: 302209
+dashedName: problem-92-square-digit-chains
+---
+
+# --description--
+
+A number chain is created by continuously adding the square of the digits in a number to form a new number until it has been seen before.
+
+For example,
+
+$$\begin{align} & 44 → 32 → 13 → 10 → \boldsymbol{1} → \boldsymbol{1}\\\\
+ & 85 → \boldsymbol{89} → 145 → 42 → 20 → 4 → 16 → 37 → 58 → \boldsymbol{89}\\\\ \end{align}$$
+
+Therefore any chain that arrives at 1 or 89 will become stuck in an endless loop. What is most amazing is that EVERY starting number will eventually arrive at 1 or 89.
+
+How many starting numbers below `limit` will arrive at 89?
+
+# --hints--
+
+`squareDigitChains(100)` should return a number.
+
+```js
+assert(typeof squareDigitChains(100) === 'number');
+```
+
+`squareDigitChains(100)` should return `80`.
+
+```js
+assert.strictEqual(squareDigitChains(100), 80);
+```
+
+`squareDigitChains(1000)` should return `857`.
+
+```js
+assert.strictEqual(squareDigitChains(1000), 857);
+```
+
+`squareDigitChains(100000)` should return `85623`.
+
+```js
+assert.strictEqual(squareDigitChains(100000), 85623);
+```
+
+`squareDigitChains(10000000)` should return `8581146`.
+
+```js
+assert.strictEqual(squareDigitChains(10000000), 8581146);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function squareDigitChains(limit) {
+
+ return true;
+}
+
+squareDigitChains(100);
+```
+
+# --solutions--
+
+```js
+function squareDigitChains(limit) {
+ // Based on https://www.xarg.org/puzzle/project-euler/problem-92/
+ function getCombinations(neededDigits, curDigits) {
+ if (neededDigits === curDigits.length) {
+ return [curDigits];
+ }
+ const combinations = [];
+ const lastDigit = curDigits.length !== 0 ? curDigits[0] : 9;
+ for (let i = 0; i <= lastDigit; i++) {
+ const results = getCombinations(neededDigits, [i].concat(curDigits));
+ combinations.push(...results);
+ }
+ return combinations;
+ }
+
+ function getPossibleSums(limit) {
+ const digitsCount = getDigits(limit).length - 1;
+ const possibleSquaredSums = [false];
+ for (let i = 1; i <= 81 * digitsCount; i++) {
+ let curVal = i;
+ while (curVal !== 1 && curVal !== 89) {
+ curVal = addSquaredDigits(curVal);
+ }
+ possibleSquaredSums[i] = curVal === 89;
+ }
+ return possibleSquaredSums;
+ }
+
+ function addSquaredDigits(num) {
+ const digits = getDigits(num);
+ let result = 0;
+ for (let i = 0; i < digits.length; i++) {
+ result += digits[i] ** 2;
+ }
+ return result;
+ }
+
+ function getDigits(number) {
+ const digits = [];
+ while (number > 0) {
+ digits.push(number % 10);
+ number = Math.floor(number / 10);
+ }
+ return digits;
+ }
+
+ function getFactorials(number) {
+ const factorials = [1];
+ for (let i = 1; i < number; i++) {
+ factorials[i] = factorials[i - 1] * i;
+ }
+ return factorials;
+ }
+
+ const neededDigits = getDigits(limit).length - 1;
+ const combinations = getCombinations(neededDigits, []);
+ const possibleSquaredDigitsSums = getPossibleSums(limit);
+ const factorials = getFactorials(neededDigits + 1);
+
+ let endingWith89 = 0;
+
+ for (let i = 0; i < combinations.length; i++) {
+ let counts = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
+ let digits = combinations[i];
+ let curSum = 0;
+ for (let j = 0; j < digits.length; j++) {
+ const curDigit = digits[j];
+ curSum += curDigit ** 2;
+ counts[curDigit]++;
+ }
+
+ if (possibleSquaredDigitsSums[curSum]) {
+ let denominator = 1;
+ for (let j = 0; j < counts.length; j++) {
+ denominator = denominator * factorials[counts[j]];
+ }
+ endingWith89 += Math.floor(
+ factorials[factorials.length - 1] / denominator
+ );
+ }
+ }
+ return endingWith89;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-93-arithmetic-expressions.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-93-arithmetic-expressions.md
new file mode 100644
index 00000000000..5a8afb7d782
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-93-arithmetic-expressions.md
@@ -0,0 +1,59 @@
+---
+id: 5900f3ca1000cf542c50fedc
+title: 'Problem 93: Arithmetic expressions'
+challengeType: 1
+forumTopicId: 302210
+dashedName: problem-93-arithmetic-expressions
+---
+
+# --description--
+
+By using each of the digits from the set, {1, 2, 3, 4}, exactly once, and making use of the four arithmetic operations (+, −, \*, /) and brackets/parentheses, it is possible to form different positive integer targets.
+
+For example,
+
+
+ 8 = (4 * (1 + 3)) / 2
+ 14 = 4 * (3 + 1 / 2)
+ 19 = 4 * (2 + 3) − 1
+ 36 = 3 * 4 * (2 + 1) +
+
+Note that concatenations of the digits, like 12 + 34, are not allowed.
+
+Using the set, {1, 2, 3, 4}, it is possible to obtain thirty-one different target numbers of which 36 is the maximum, and each of the numbers 1 to 28 can be obtained before encountering the first non-expressible number.
+
+Find the set of four distinct digits, `a` < `b` < `c` < `d`, for which the longest set of consecutive positive integers, 1 to `n`, can be obtained, giving your answer as a string: `abcd`.
+
+# --hints--
+
+`arithmeticExpressions()` should return a number.
+
+```js
+assert(typeof arithmeticExpressions() === 'number');
+```
+
+`arithmeticExpressions()` should return 1258.
+
+```js
+assert.strictEqual(arithmeticExpressions(), 1258);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function arithmeticExpressions() {
+
+ return true;
+}
+
+arithmeticExpressions();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-94-almost-equilateral-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-94-almost-equilateral-triangles.md
new file mode 100644
index 00000000000..4b3ab85e079
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-94-almost-equilateral-triangles.md
@@ -0,0 +1,84 @@
+---
+id: 5900f3ca1000cf542c50fedd
+title: 'Problem 94: Almost equilateral triangles'
+challengeType: 1
+forumTopicId: 302211
+dashedName: problem-94-almost-equilateral-triangles
+---
+
+# --description--
+
+It is easily proved that no equilateral triangle exists with integral length sides and integral area. However, the almost equilateral triangle 5-5-6 has an area of 12 square units.
+
+We shall define an almost equilateral triangle to be a triangle for which two sides are equal and the third differs by no more than one unit.
+
+Find the sum of the perimeters of all almost equilateral triangles with integral side lengths and area and whose perimeters do not exceed `limit`.
+
+# --hints--
+
+`almostEquilateralTriangles(50)` should return a number.
+
+```js
+assert(typeof almostEquilateralTriangles(50) === 'number');
+```
+
+`almostEquilateralTriangles(50)` should return `66`.
+
+```js
+assert.strictEqual(almostEquilateralTriangles(50), 66);
+```
+
+`almostEquilateralTriangles(10000)` should return `3688`.
+
+```js
+assert.strictEqual(almostEquilateralTriangles(10000), 3688);
+```
+
+`almostEquilateralTriangles(10000000)` should return `9973078`.
+
+```js
+assert.strictEqual(almostEquilateralTriangles(10000000), 9973078);
+```
+
+`almostEquilateralTriangles(1000000000)` should return `518408346`.
+
+```js
+assert.strictEqual(almostEquilateralTriangles(1000000000), 518408346);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function almostEquilateralTriangles(limit) {
+
+ return true;
+}
+
+almostEquilateralTriangles(50);
+```
+
+# --solutions--
+
+```js
+function almostEquilateralTriangles(limit) {
+ // Based on https://blog.dreamshire.com/project-euler-94-solution/
+ let perimetersSum = 0;
+
+ let sidesAB = 1;
+ let sideC = 1;
+ let perimeter = 0;
+ let perimeterOffset = 1;
+
+ while (perimeter <= limit) {
+ [sidesAB, sideC] = [4 * sidesAB - sideC + 2 * perimeterOffset, sidesAB];
+ perimeterOffset = -perimeterOffset;
+
+ perimetersSum += perimeter;
+ perimeter = 3 * sidesAB - perimeterOffset;
+ }
+
+ return perimetersSum;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-95-amicable-chains.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-95-amicable-chains.md
new file mode 100644
index 00000000000..fe2d422a206
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-95-amicable-chains.md
@@ -0,0 +1,124 @@
+---
+id: 5900f3cc1000cf542c50fede
+title: 'Problem 95: Amicable chains'
+challengeType: 1
+forumTopicId: 302212
+dashedName: problem-95-amicable-chains
+---
+
+# --description--
+
+The proper divisors of a number are all the divisors excluding the number itself. For example, the proper divisors of 28 are 1, 2, 4, 7, and 14. As the sum of these divisors is equal to 28, we call it a perfect number.
+
+Interestingly the sum of the proper divisors of 220 is 284 and the sum of the proper divisors of 284 is 220, forming a chain of two numbers. For this reason, 220 and 284 are called an amicable pair.
+
+Perhaps less well known are longer chains. For example, starting with 12496, we form a chain of five numbers:
+
+$$ 12496 → 14288 → 15472 → 14536 → 14264 \\,(→ 12496 → \cdots) $$
+
+Since this chain returns to its starting point, it is called an amicable chain.
+
+Find the smallest member of the longest amicable chain with no element exceeding `limit`.
+
+# --hints--
+
+`amicableChains(300)` should return a number.
+
+```js
+assert(typeof amicableChains(300) === 'number');
+```
+
+`amicableChains(300)` should return `220`.
+
+```js
+assert.strictEqual(amicableChains(300), 220);
+```
+
+`amicableChains(15000)` should return `220`.
+
+```js
+assert.strictEqual(amicableChains(15000), 220);
+```
+
+`amicableChains(100000)` should return `12496`.
+
+```js
+assert.strictEqual(amicableChains(100000), 12496);
+```
+
+`amicableChains(1000000)` should return `14316`.
+
+```js
+assert.strictEqual(amicableChains(1000000), 14316);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function amicableChains(limit) {
+
+ return true;
+}
+
+amicableChains(300);
+```
+
+# --solutions--
+
+```js
+function amicableChains(limit) {
+ function getSmallestMember(chain) {
+ let smallest = chain[0];
+ for (let i = 1; i < chain.length; i++) {
+ if (smallest > chain[i]) {
+ smallest = chain[i];
+ }
+ }
+ return smallest;
+ }
+
+ function getFactorsSums(limit) {
+ const factorsSums = new Array(limit + 1).fill(1);
+ for (let i = 2; i <= limit / 2; i++) {
+ for (let j = 2 * i; j <= limit; j += i) {
+ factorsSums[j] += i;
+ }
+ }
+ return factorsSums;
+ }
+
+ const factorsSums = getFactorsSums(limit);
+ const checkedNumbers = new Set();
+
+ let longestChain = 0;
+ let smallestMember = 0;
+ for (let i = 0; i <= limit; i++) {
+ const curChain = [];
+ let curNumber = i;
+ while (!checkedNumbers.has(curNumber) && factorsSums[curNumber] <= limit) {
+ curNumber = factorsSums[curNumber];
+
+ const chainStart = curChain.indexOf(curNumber);
+ if (chainStart === -1) {
+ curChain.push(curNumber);
+ continue;
+ }
+
+ const chainLength = curChain.length - chainStart;
+ if (chainLength > longestChain) {
+ longestChain = chainLength;
+ smallestMember = getSmallestMember(curChain.slice(chainStart));
+ }
+ break;
+ }
+
+ for (let j = 0; j < curChain.length; j++) {
+ checkedNumbers.add(curChain[j]);
+ }
+ }
+
+ return smallestMember;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-96-su-doku.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-96-su-doku.md
new file mode 100644
index 00000000000..098fdb0d398
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-96-su-doku.md
@@ -0,0 +1,296 @@
+---
+id: 5900f3cc1000cf542c50fedf
+title: 'Problem 96: Su Doku'
+challengeType: 1
+forumTopicId: 302213
+dashedName: problem-96-su-doku
+---
+
+# --description--
+
+Su Doku (Japanese meaning *number place*) is the name given to a popular puzzle concept. Its origin is unclear, but credit must be attributed to Leonhard Euler who invented a similar, and much more difficult, puzzle idea called Latin Squares. The objective of Su Doku puzzles, however, is to replace the blanks (or zeros) in a 9 by 9 grid in such that each row, column, and 3 by 3 box contains each of the digits 1 to 9. Below is an example of a typical starting puzzle grid and its solution grid.
+
++ 14 = 4 * (3 + 1 / 2)
+ 19 = 4 * (2 + 3) − 1
+ 36 = 3 * 4 * (2 + 1) +
+
+
+
+
+
+A well constructed Su Doku puzzle has a unique solution and can be solved by logic, although it may be necessary to employ "guess and test" methods in order to eliminate options (there is much contested opinion over this). The complexity of the search determines the difficulty of the puzzle; the example above is considered easy because it can be solved by straight forward direct deduction.
+
+The `puzzlesArr` array contains different Su Doku puzzle strings ranging in difficulty, but all with unique solutions.
+
+By solving all puzzles in `puzzlesArr`, find the sum of the 3-digit numbers found in the top left corner of each solution grid; for example, 483 is the 3-digit number found in the top left corner of the solution grid above.
+
+# --hints--
+
+`suDoku(testPuzzles1)` should return a number.
+
+```js
+assert(typeof suDoku(_testPuzzles1) === 'number');
+```
+
+`suDoku(testPuzzles1)` should return `1190`.
+
+```js
+assert.strictEqual(suDoku(_testPuzzles1), 1190);
+```
+
+`suDoku(testPuzzles2)` should return `24702`.
+
+```js
+assert.strictEqual(suDoku(_testPuzzles2), 24702);
+```
+
+# --seed--
+
+## --after-user-code--
+
+```js
+const _testPuzzles1 = [
+ '003020600900305001001806400008102900700000008006708200002609500800203009005010300',
+ '200080300060070084030500209000105408000000000402706000301007040720040060004010003',
+ '000000907000420180000705026100904000050000040000507009920108000034059000507000000'
+];
+
+const _testPuzzles2 = [
+ '003020600900305001001806400008102900700000008006708200002609500800203009005010300',
+ '200080300060070084030500209000105408000000000402706000301007040720040060004010003',
+ '000000907000420180000705026100904000050000040000507009920108000034059000507000000',
+ '030050040008010500460000012070502080000603000040109030250000098001020600080060020',
+ '020810740700003100090002805009040087400208003160030200302700060005600008076051090',
+ '100920000524010000000000070050008102000000000402700090060000000000030945000071006',
+ '043080250600000000000001094900004070000608000010200003820500000000000005034090710',
+ '480006902002008001900370060840010200003704100001060049020085007700900600609200018',
+ '000900002050123400030000160908000000070000090000000205091000050007439020400007000',
+ '001900003900700160030005007050000009004302600200000070600100030042007006500006800',
+ '000125400008400000420800000030000095060902010510000060000003049000007200001298000',
+ '062340750100005600570000040000094800400000006005830000030000091006400007059083260',
+ '300000000005009000200504000020000700160000058704310600000890100000067080000005437',
+ '630000000000500008005674000000020000003401020000000345000007004080300902947100080',
+ '000020040008035000000070602031046970200000000000501203049000730000000010800004000',
+ '361025900080960010400000057008000471000603000259000800740000005020018060005470329',
+ '050807020600010090702540006070020301504000908103080070900076205060090003080103040',
+ '080005000000003457000070809060400903007010500408007020901020000842300000000100080',
+ '003502900000040000106000305900251008070408030800763001308000104000020000005104800',
+ '000000000009805100051907420290401065000000000140508093026709580005103600000000000',
+ '020030090000907000900208005004806500607000208003102900800605007000309000030020050',
+ '005000006070009020000500107804150000000803000000092805907006000030400010200000600',
+ '040000050001943600009000300600050002103000506800020007005000200002436700030000040',
+ '004000000000030002390700080400009001209801307600200008010008053900040000000000800',
+ '360020089000361000000000000803000602400603007607000108000000000000418000970030014',
+ '500400060009000800640020000000001008208000501700500000000090084003000600060003002',
+ '007256400400000005010030060000508000008060200000107000030070090200000004006312700',
+ '000000000079050180800000007007306800450708096003502700700000005016030420000000000',
+ '030000080009000500007509200700105008020090030900402001004207100002000800070000090',
+ '200170603050000100000006079000040700000801000009050000310400000005000060906037002',
+ '000000080800701040040020030374000900000030000005000321010060050050802006080000000',
+ '000000085000210009960080100500800016000000000890006007009070052300054000480000000',
+ '608070502050608070002000300500090006040302050800050003005000200010704090409060701',
+ '050010040107000602000905000208030501040070020901080406000401000304000709020060010',
+ '053000790009753400100000002090080010000907000080030070500000003007641200061000940',
+ '006080300049070250000405000600317004007000800100826009000702000075040190003090600',
+ '005080700700204005320000084060105040008000500070803010450000091600508007003010600',
+ '000900800128006400070800060800430007500000009600079008090004010003600284001007000',
+ '000080000270000054095000810009806400020403060006905100017000620460000038000090000',
+ '000602000400050001085010620038206710000000000019407350026040530900020007000809000',
+ '000900002050123400030000160908000000070000090000000205091000050007439020400007000',
+ '380000000000400785009020300060090000800302009000040070001070500495006000000000092',
+ '000158000002060800030000040027030510000000000046080790050000080004070100000325000',
+ '010500200900001000002008030500030007008000500600080004040100700000700006003004050',
+ '080000040000469000400000007005904600070608030008502100900000005000781000060000010',
+ '904200007010000000000706500000800090020904060040002000001607000000000030300005702',
+ '000700800006000031040002000024070000010030080000060290000800070860000500002006000',
+ '001007090590080001030000080000005800050060020004100000080000030100020079020700400',
+ '000003017015009008060000000100007000009000200000500004000000020500600340340200000',
+ '300200000000107000706030500070009080900020004010800050009040301000702000000008006'
+];
+```
+
+## --seed-contents--
+
+```js
+function suDoku(puzzlesArr) {
+
+ return true;
+}
+
+// Only change code above this line
+
+const testPuzzles1 = [
+ '003020600900305001001806400008102900700000008006708200002609500800203009005010300',
+ '200080300060070084030500209000105408000000000402706000301007040720040060004010003',
+ '000000907000420180000705026100904000050000040000507009920108000034059000507000000'
+];
+
+suDoku(testPuzzles1);
+```
+
+# --solutions--
+
+```js
+function suDoku(puzzlesArr) {
+ function solve(puzzle) {
+ for (let row = 0; row < 9; row++) {
+ for (let col = 0; col < 9; col++) {
+ if (puzzle[row][col] > 0) {
+ continue;
+ }
+
+ const allowedNumbers = getAllowedNumbers(puzzle, row, col);
+
+ for (let number = 1; number <= 9; number++) {
+ if (allowedNumbers[number]) {
+ puzzle[row][col] = number;
+ if (solve(puzzle)) {
+ return true;
+ }
+ }
+ }
+
+ puzzle[row][col] = 0;
+ return false;
+ }
+ }
+ return true;
+ }
+
+ function getAllowedNumbers(puzzle, row, col) {
+ const allowed = new Array(10).fill(true);
+ allowed[0] = false;
+
+ for (let i = 0; i < 9; i++) {
+ const numberInSameRow = puzzle[row][i];
+ if (numberInSameRow > 0) {
+ allowed[numberInSameRow] = false;
+ }
+
+ const numberInSameCol = puzzle[i][col];
+ if (numberInSameCol > 0) {
+ allowed[numberInSameCol] = false;
+ }
+ }
+
+ const rowOfSubGrid = Math.floor(row / 3) * 3;
+ const colOfSubGrid = Math.floor(col / 3) * 3;
+ for (let rowInSubGrid = 0; rowInSubGrid < 3; rowInSubGrid++) {
+ for (let colInSubGrid = 0; colInSubGrid < 3; colInSubGrid++) {
+ const numberInSameSubGrid =
+ puzzle[rowOfSubGrid + rowInSubGrid][colOfSubGrid + colInSubGrid];
+ if (numberInSameSubGrid > 0) {
+ allowed[numberInSameSubGrid] = false;
+ }
+ }
+ }
+
+ return allowed;
+ }
+
+ function parsePuzzle(string) {
+ const puzzle = [];
+ for (let row = 0; row < 9; row++) {
+ puzzle.push(
+ string
+ .slice(row * 9, 9 + row * 9)
+ .split('')
+ .map(x => parseInt(x, 10))
+ );
+ }
+ return puzzle;
+ }
+
+ let sum = 0;
+ for (let i = 0; i < puzzlesArr.length; i++) {
+ const puzzle = parsePuzzle(puzzlesArr[i]);
+ if (solve(puzzle)) {
+ sum += 100 * puzzle[0][0] + 10 * puzzle[0][1] + puzzle[0][2];
+ }
+ }
+
+ return sum;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-97-large-non-mersenne-prime.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-97-large-non-mersenne-prime.md
new file mode 100644
index 00000000000..cabdb3486c9
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-97-large-non-mersenne-prime.md
@@ -0,0 +1,88 @@
+---
+id: 5900f3ce1000cf542c50fee0
+title: 'Problem 97: Large non-Mersenne prime'
+challengeType: 1
+forumTopicId: 302214
+dashedName: problem-97-large-non-mersenne-prime
+---
+
+# --description--
+
+The first known prime found to exceed one million digits was discovered in 1999, and is a Mersenne prime of the form $2^{6972593} − 1$; it contains exactly 2,098,960 digits. Subsequently other Mersenne primes, of the form $2^p − 1$, have been found which contain more digits.
+
+However, in 2004 there was found a massive non-Mersenne prime which contains 2,357,207 digits: $28433 × 2^{7830457} + 1$.
+
+Find the last ten digits of that non-Mersenne prime in the form $multiplier × 2^{power} + 1$.
+
+# --hints--
+
+`largeNonMersennePrime(19, 6833086)` should return a string.
+
+```js
+assert(typeof largeNonMersennePrime(19, 6833086) === 'string');
+```
+
+`largeNonMersennePrime(19, 6833086)` should return the string `3637590017`.
+
+```js
+assert.strictEqual(largeNonMersennePrime(19, 6833086), '3637590017');
+```
+
+`largeNonMersennePrime(27, 7046834)` should return the string `0130771969`.
+
+```js
+assert.strictEqual(largeNonMersennePrime(27, 7046834), '0130771969');
+```
+
+`largeNonMersennePrime(6679881, 6679881)` should return the string `4455386113`.
+
+```js
+assert.strictEqual(largeNonMersennePrime(6679881, 6679881), '4455386113');
+```
+
+`largeNonMersennePrime(28433, 7830457)` should return the string `8739992577`.
+
+```js
+assert.strictEqual(largeNonMersennePrime(28433, 7830457), '8739992577');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function largeNonMersennePrime(multiplier, power) {
+
+ return true;
+}
+
+largeNonMersennePrime(19, 6833086);
+```
+
+# --solutions--
+
+```js
+function largeNonMersennePrime(multiplier, power) {
+ function modStepsResults(number, other, mod, startValue, step) {
+ let result = startValue;
+ for (let i = 0; i < other; i++) {
+ result = step(number, result) % mod;
+ }
+ return result;
+ }
+
+ const numOfDigits = 10;
+ const mod = 10 ** numOfDigits;
+ const digitsAfterPower = modStepsResults(2, power, mod, 1, (a, b) => a * b);
+ const digitsAfterMultiply = modStepsResults(
+ digitsAfterPower,
+ multiplier,
+ mod,
+ 0,
+ (a, b) => a + b
+ );
+ const lastDigits = (digitsAfterMultiply + 1) % mod;
+
+ return lastDigits.toString().padStart(10, '0');
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-98-anagramic-squares.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-98-anagramic-squares.md
new file mode 100644
index 00000000000..f54ab71dd62
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-98-anagramic-squares.md
@@ -0,0 +1,205 @@
+---
+id: 5900f3cf1000cf542c50fee1
+title: 'Problem 98: Anagramic squares'
+challengeType: 1
+forumTopicId: 302215
+dashedName: problem-98-anagramic-squares
+---
+
+# --description--
+
+By replacing each of the letters in the word CARE with 1, 2, 9, and 6 respectively, we form a square number: $1296 = 36^2$. What is remarkable is that, by using the same digital substitutions, the anagram, RACE, also forms a square number: $9216 = 96^2$. We shall call CARE (and RACE) a square anagram word pair and specify further that leading zeroes are not permitted, neither may a different letter have the same digital value as another letter.
+
+Using the `words` array, find all the square anagram word pairs (a palindromic word is NOT considered to be an anagram of itself).
+
+What is the largest square number formed by any member of such a pair?
+
+**Note:** All anagrams formed must be contained in the given `words` array.
+
+# --hints--
+
+`anagramicSquares(['CARE', 'RACE'])` should return a number.
+
+```js
+assert(typeof anagramicSquares(['CARE', 'RACE']) === 'number');
+```
+
+`anagramicSquares(['CARE', 'RACE'])` should return `9216`.
+
+```js
+assert.strictEqual(anagramicSquares(['CARE', 'RACE']), 9216);
+```
+
+`anagramicSquares(testWords1)` should return `4761`.
+
+```js
+assert.strictEqual(anagramicSquares(_testWords1), 4761);
+```
+
+`anagramicSquares(testWords2)` should return `18769`.
+
+```js
+assert.strictEqual(anagramicSquares(_testWords2), 18769);
+```
+
+# --seed--
+
+## --after-user-code--
+
+```js
+const _testWords1 = [
+ "DAMAGE","DANGER","DANGEROUS","DARK","DATA","DATE","DAUGHTER","DAY","DEAD","DEAL","DEATH","DEBATE","DEBT","DECADE","DECIDE","DECISION","DECLARE","DEEP","DEFENCE","DEFENDANT","DEFINE","DEFINITION","DEGREE","DELIVER","DEMAND","DEMOCRATIC","DEMONSTRATE","DENY","DEPARTMENT","DEPEND","DEPUTY","DERIVE","DESCRIBE","DESCRIPTION","DESIGN","DESIRE","DESK","DESPITE","DESTROY","DETAIL","DETAILED","DETERMINE","DEVELOP","DEVELOPMENT","DEVICE","DIE","DIFFERENCE","DIFFERENT","DIFFICULT","DIFFICULTY","DINNER","DIRECT","DIRECTION","DIRECTLY","DIRECTOR","DISAPPEAR","DISCIPLINE","DISCOVER","DISCUSS","DISCUSSION","DISEASE","DISPLAY","DISTANCE","DISTINCTION","DISTRIBUTION","DISTRICT","DIVIDE","DIVISION","DO","DOCTOR","DOCUMENT","DOG","DOMESTIC","DOOR","DOUBLE","DOUBT","DOWN","DRAW","DRAWING","DREAM","DRESS","DRINK","DRIVE","DRIVER","DROP","DRUG","DRY","DUE","DURING","DUTY","LABOUR","LACK","LADY","LAND","LANGUAGE","LARGE","LARGELY","LAST","LATE","LATER","LATTER","LAUGH","LAUNCH","LAW","LAWYER","LAY","LEAD","LEADER","LEADERSHIP","LEADING","LEAF","LEAGUE","LEAN","LEARN","LEAST","LEAVE","LEFT","LEG","LEGAL","LEGISLATION","LENGTH","LESS","LET","LETTER","LEVEL","LIABILITY","LIBERAL","LIBRARY","LIE","LIFE","LIFT","LIGHT","LIKE","LIKELY","LIMIT","LIMITED","LINE","LINK","LIP","LIST","LISTEN","LITERATURE","LITTLE","LIVE","LIVING","LOAN","LOCAL","LOCATION","LONG","LOOK","LORD","LOSE","LOSS","LOT","LOVE","LOVELY","LOW","LUNCH"
+];
+const _testWords2 = [
+ "A","ABILITY","ABLE","ABOUT","ABOVE","ABSENCE","ABSOLUTELY","ACADEMIC","ACCEPT","ACCESS","ACCIDENT","ACCOMPANY","ACCORDING","ACCOUNT","ACHIEVE","ACHIEVEMENT","ACID","ACQUIRE","ACROSS","ACT","ACTION","ACTIVE","ACTIVITY","ACTUAL","ACTUALLY","ADD","ADDITION","ADDITIONAL","ADDRESS","ADMINISTRATION","ADMIT","ADOPT","ADULT","ADVANCE","ADVANTAGE","ADVICE","ADVISE","AFFAIR","AFFECT","AFFORD","AFRAID","AFTER","AFTERNOON","AFTERWARDS","AGAIN","AGAINST","AGE","AGENCY","AGENT","AGO","AGREE","AGREEMENT","AHEAD","AID","AIM","AIR","AIRCRAFT","ALL","ALLOW","ALMOST","ALONE","ALONG","ALREADY","ALRIGHT","ALSO","ALTERNATIVE","ALTHOUGH","ALWAYS","AMONG","AMONGST","AMOUNT","AN","ANALYSIS","ANCIENT","AND","ANIMAL","ANNOUNCE","ANNUAL","ANOTHER","ANSWER","ANY","ANYBODY","ANYONE","ANYTHING","ANYWAY","APART","APPARENT","APPARENTLY","APPEAL","APPEAR","APPEARANCE","APPLICATION","APPLY","APPOINT","APPOINTMENT","APPROACH","APPROPRIATE","APPROVE","AREA","ARGUE","ARGUMENT","ARISE","ARM","ARMY","AROUND","ARRANGE","ARRANGEMENT","ARRIVE","ART","ARTICLE","ARTIST","AS","ASK","ASPECT","ASSEMBLY","ASSESS","ASSESSMENT","ASSET","ASSOCIATE","ASSOCIATION","ASSUME","ASSUMPTION","AT","ATMOSPHERE","ATTACH","ATTACK","ATTEMPT","ATTEND","ATTENTION","ATTITUDE","ATTRACT","ATTRACTIVE","AUDIENCE","AUTHOR","AUTHORITY","AVAILABLE","AVERAGE","AVOID","AWARD","AWARE","AWAY","AYE","BABY","BACK","BACKGROUND","BAD","BAG","BALANCE","BALL","BAND","BANK","BAR","BASE","BASIC","BASIS","BATTLE","BE","BEAR","BEAT","BEAUTIFUL","BECAUSE","BECOME","BED","BEDROOM","BEFORE","BEGIN","BEGINNING","BEHAVIOUR","BEHIND","BELIEF","BELIEVE","BELONG","BELOW","BENEATH","BENEFIT","BESIDE","BEST","BETTER","BETWEEN","BEYOND","BIG","BILL","BIND","BIRD","BIRTH","BIT","BLACK","BLOCK","BLOOD","BLOODY","BLOW","BLUE","BOARD","BOAT","BODY","BONE","BOOK","BORDER","BOTH","BOTTLE","BOTTOM","BOX","BOY","BRAIN","BRANCH","BREAK","BREATH","BRIDGE","BRIEF","BRIGHT","BRING","BROAD","BROTHER","BUDGET","BUILD","BUILDING","BURN","BUS","BUSINESS","BUSY","BUT","BUY","BY","CABINET","CALL","CAMPAIGN","CAN","CANDIDATE","CAPABLE","CAPACITY","CAPITAL","CAR","CARD","CARE","CAREER","CAREFUL","CAREFULLY","CARRY","CASE","CASH","CAT","CATCH","CATEGORY","CAUSE","CELL","CENTRAL","CENTRE","CENTURY","CERTAIN","CERTAINLY","CHAIN","CHAIR","CHAIRMAN","CHALLENGE","CHANCE","CHANGE","CHANNEL","CHAPTER","CHARACTER","CHARACTERISTIC","CHARGE","CHEAP","CHECK","CHEMICAL","CHIEF","CHILD","CHOICE","CHOOSE","CHURCH","CIRCLE","CIRCUMSTANCE","CITIZEN","CITY","CIVIL","CLAIM","CLASS","CLEAN","CLEAR","CLEARLY","CLIENT","CLIMB","CLOSE","CLOSELY","CLOTHES","CLUB","COAL","CODE","COFFEE","COLD","COLLEAGUE","COLLECT","COLLECTION","COLLEGE","COLOUR","COMBINATION","COMBINE","COME","COMMENT","COMMERCIAL","COMMISSION","COMMIT","COMMITMENT","COMMITTEE","COMMON","COMMUNICATION","COMMUNITY","COMPANY","COMPARE","COMPARISON","COMPETITION","COMPLETE","COMPLETELY","COMPLEX","COMPONENT","COMPUTER","CONCENTRATE","CONCENTRATION","CONCEPT","CONCERN","CONCERNED","CONCLUDE","CONCLUSION","CONDITION","CONDUCT","CONFERENCE","CONFIDENCE","CONFIRM","CONFLICT","CONGRESS","CONNECT","CONNECTION","CONSEQUENCE","CONSERVATIVE","CONSIDER","CONSIDERABLE","CONSIDERATION","CONSIST","CONSTANT","CONSTRUCTION","CONSUMER","CONTACT","CONTAIN","CONTENT","CONTEXT","CONTINUE","CONTRACT","CONTRAST","CONTRIBUTE","CONTRIBUTION","CONTROL","CONVENTION","CONVERSATION","COPY","CORNER","CORPORATE","CORRECT","COS","COST","COULD","COUNCIL","COUNT","COUNTRY","COUNTY","COUPLE","COURSE","COURT","COVER","CREATE","CREATION","CREDIT","CRIME","CRIMINAL","CRISIS","CRITERION","CRITICAL","CRITICISM","CROSS","CROWD","CRY","CULTURAL","CULTURE","CUP","CURRENT","CURRENTLY","CURRICULUM","CUSTOMER","CUT","DAMAGE","DANGER","DANGEROUS","DARK","DATA","DATE","DAUGHTER","DAY","DEAD","DEAL","DEATH","DEBATE","DEBT","DECADE","DECIDE","DECISION","DECLARE","DEEP","DEFENCE","DEFENDANT","DEFINE","DEFINITION","DEGREE","DELIVER","DEMAND","DEMOCRATIC","DEMONSTRATE","DENY","DEPARTMENT","DEPEND","DEPUTY","DERIVE","DESCRIBE","DESCRIPTION","DESIGN","DESIRE","DESK","DESPITE","DESTROY","DETAIL","DETAILED","DETERMINE","DEVELOP","DEVELOPMENT","DEVICE","DIE","DIFFERENCE","DIFFERENT","DIFFICULT","DIFFICULTY","DINNER","DIRECT","DIRECTION","DIRECTLY","DIRECTOR","DISAPPEAR","DISCIPLINE","DISCOVER","DISCUSS","DISCUSSION","DISEASE","DISPLAY","DISTANCE","DISTINCTION","DISTRIBUTION","DISTRICT","DIVIDE","DIVISION","DO","DOCTOR","DOCUMENT","DOG","DOMESTIC","DOOR","DOUBLE","DOUBT","DOWN","DRAW","DRAWING","DREAM","DRESS","DRINK","DRIVE","DRIVER","DROP","DRUG","DRY","DUE","DURING","DUTY","EACH","EAR","EARLY","EARN","EARTH","EASILY","EAST","EASY","EAT","ECONOMIC","ECONOMY","EDGE","EDITOR","EDUCATION","EDUCATIONAL","EFFECT","EFFECTIVE","EFFECTIVELY","EFFORT","EGG","EITHER","ELDERLY","ELECTION","ELEMENT","ELSE","ELSEWHERE","EMERGE","EMPHASIS","EMPLOY","EMPLOYEE","EMPLOYER","EMPLOYMENT","EMPTY","ENABLE","ENCOURAGE","END","ENEMY","ENERGY","ENGINE","ENGINEERING","ENJOY","ENOUGH","ENSURE","ENTER","ENTERPRISE","ENTIRE","ENTIRELY","ENTITLE","ENTRY","ENVIRONMENT","ENVIRONMENTAL","EQUAL","EQUALLY","EQUIPMENT","ERROR","ESCAPE","ESPECIALLY","ESSENTIAL","ESTABLISH","ESTABLISHMENT","ESTATE","ESTIMATE","EVEN","EVENING","EVENT","EVENTUALLY","EVER","EVERY","EVERYBODY","EVERYONE","EVERYTHING","EVIDENCE","EXACTLY","EXAMINATION","EXAMINE","EXAMPLE","EXCELLENT","EXCEPT","EXCHANGE","EXECUTIVE","EXERCISE","EXHIBITION","EXIST","EXISTENCE","EXISTING","EXPECT","EXPECTATION","EXPENDITURE","EXPENSE","EXPENSIVE","EXPERIENCE","EXPERIMENT","EXPERT","EXPLAIN","EXPLANATION","EXPLORE","EXPRESS","EXPRESSION","EXTEND","EXTENT","EXTERNAL","EXTRA","EXTREMELY","EYE","FACE","FACILITY","FACT","FACTOR","FACTORY","FAIL","FAILURE","FAIR","FAIRLY","FAITH","FALL","FAMILIAR","FAMILY","FAMOUS","FAR","FARM","FARMER","FASHION","FAST","FATHER","FAVOUR","FEAR","FEATURE","FEE","FEEL","FEELING","FEMALE","FEW","FIELD","FIGHT","FIGURE","FILE","FILL","FILM","FINAL","FINALLY","FINANCE","FINANCIAL","FIND","FINDING","FINE","FINGER","FINISH","FIRE","FIRM","FIRST","FISH","FIT","FIX","FLAT","FLIGHT","FLOOR","FLOW","FLOWER","FLY","FOCUS","FOLLOW","FOLLOWING","FOOD","FOOT","FOOTBALL","FOR","FORCE","FOREIGN","FOREST","FORGET","FORM","FORMAL","FORMER","FORWARD","FOUNDATION","FREE","FREEDOM","FREQUENTLY","FRESH","FRIEND","FROM","FRONT","FRUIT","FUEL","FULL","FULLY","FUNCTION","FUND","FUNNY","FURTHER","FUTURE","GAIN","GAME","GARDEN","GAS","GATE","GATHER","GENERAL","GENERALLY","GENERATE","GENERATION","GENTLEMAN","GET","GIRL","GIVE","GLASS","GO","GOAL","GOD","GOLD","GOOD","GOVERNMENT","GRANT","GREAT","GREEN","GREY","GROUND","GROUP","GROW","GROWING","GROWTH","GUEST","GUIDE","GUN","HAIR","HALF","HALL","HAND","HANDLE","HANG","HAPPEN","HAPPY","HARD","HARDLY","HATE","HAVE","HE","HEAD","HEALTH","HEAR","HEART","HEAT","HEAVY","HELL","HELP","HENCE","HER","HERE","HERSELF","HIDE","HIGH","HIGHLY","HILL","HIM","HIMSELF","HIS","HISTORICAL","HISTORY","HIT","HOLD","HOLE","HOLIDAY","HOME","HOPE","HORSE","HOSPITAL","HOT","HOTEL","HOUR","HOUSE","HOUSEHOLD","HOUSING","HOW","HOWEVER","HUGE","HUMAN","HURT","HUSBAND","I","IDEA","IDENTIFY","IF","IGNORE","ILLUSTRATE","IMAGE","IMAGINE","IMMEDIATE","IMMEDIATELY","IMPACT","IMPLICATION","IMPLY","IMPORTANCE","IMPORTANT","IMPOSE","IMPOSSIBLE","IMPRESSION","IMPROVE","IMPROVEMENT","IN","INCIDENT","INCLUDE","INCLUDING","INCOME","INCREASE","INCREASED","INCREASINGLY","INDEED","INDEPENDENT","INDEX","INDICATE","INDIVIDUAL","INDUSTRIAL","INDUSTRY","INFLUENCE","INFORM","INFORMATION","INITIAL","INITIATIVE","INJURY","INSIDE","INSIST","INSTANCE","INSTEAD","INSTITUTE","INSTITUTION","INSTRUCTION","INSTRUMENT","INSURANCE","INTEND","INTENTION","INTEREST","INTERESTED","INTERESTING","INTERNAL","INTERNATIONAL","INTERPRETATION","INTERVIEW","INTO","INTRODUCE","INTRODUCTION","INVESTIGATE","INVESTIGATION","INVESTMENT","INVITE","INVOLVE","IRON","IS","ISLAND","ISSUE","IT","ITEM","ITS","ITSELF","JOB","JOIN","JOINT","JOURNEY","JUDGE","JUMP","JUST","JUSTICE","KEEP","KEY","KID","KILL","KIND","KING","KITCHEN","KNEE","KNOW","KNOWLEDGE","LABOUR","LACK","LADY","LAND","LANGUAGE","LARGE","LARGELY","LAST","LATE","LATER","LATTER","LAUGH","LAUNCH","LAW","LAWYER","LAY","LEAD","LEADER","LEADERSHIP","LEADING","LEAF","LEAGUE","LEAN","LEARN","LEAST","LEAVE","LEFT","LEG","LEGAL","LEGISLATION","LENGTH","LESS","LET","LETTER","LEVEL","LIABILITY","LIBERAL","LIBRARY","LIE","LIFE","LIFT","LIGHT","LIKE","LIKELY","LIMIT","LIMITED","LINE","LINK","LIP","LIST","LISTEN","LITERATURE","LITTLE","LIVE","LIVING","LOAN","LOCAL","LOCATION","LONG","LOOK","LORD","LOSE","LOSS","LOT","LOVE","LOVELY","LOW","LUNCH","MACHINE","MAGAZINE","MAIN","MAINLY","MAINTAIN","MAJOR","MAJORITY","MAKE","MALE","MAN","MANAGE","MANAGEMENT","MANAGER","MANNER","MANY","MAP","MARK","MARKET","MARRIAGE","MARRIED","MARRY","MASS","MASTER","MATCH","MATERIAL","MATTER","MAY","MAYBE","ME","MEAL","MEAN","MEANING","MEANS","MEANWHILE","MEASURE","MECHANISM","MEDIA","MEDICAL","MEET","MEETING","MEMBER","MEMBERSHIP","MEMORY","MENTAL","MENTION","MERELY","MESSAGE","METAL","METHOD","MIDDLE","MIGHT","MILE","MILITARY","MILK","MIND","MINE","MINISTER","MINISTRY","MINUTE","MISS","MISTAKE","MODEL","MODERN","MODULE","MOMENT","MONEY","MONTH","MORE","MORNING","MOST","MOTHER","MOTION","MOTOR","MOUNTAIN","MOUTH","MOVE","MOVEMENT","MUCH","MURDER","MUSEUM","MUSIC","MUST","MY","MYSELF","NAME","NARROW","NATION","NATIONAL","NATURAL","NATURE","NEAR","NEARLY","NECESSARILY","NECESSARY","NECK","NEED","NEGOTIATION","NEIGHBOUR","NEITHER","NETWORK","NEVER","NEVERTHELESS","NEW","NEWS","NEWSPAPER","NEXT","NICE","NIGHT","NO","NOBODY","NOD","NOISE","NONE","NOR","NORMAL","NORMALLY","NORTH","NORTHERN","NOSE","NOT","NOTE","NOTHING","NOTICE","NOTION","NOW","NUCLEAR","NUMBER","NURSE","OBJECT","OBJECTIVE","OBSERVATION","OBSERVE","OBTAIN","OBVIOUS","OBVIOUSLY","OCCASION","OCCUR","ODD","OF","OFF","OFFENCE","OFFER","OFFICE","OFFICER","OFFICIAL","OFTEN","OIL","OKAY","OLD","ON","ONCE","ONE","ONLY","ONTO","OPEN","OPERATE","OPERATION","OPINION","OPPORTUNITY","OPPOSITION","OPTION","OR","ORDER","ORDINARY","ORGANISATION","ORGANISE","ORGANIZATION","ORIGIN","ORIGINAL","OTHER","OTHERWISE","OUGHT","OUR","OURSELVES","OUT","OUTCOME","OUTPUT","OUTSIDE","OVER","OVERALL","OWN","OWNER","PACKAGE","PAGE","PAIN","PAINT","PAINTING","PAIR","PANEL","PAPER","PARENT","PARK","PARLIAMENT","PART","PARTICULAR","PARTICULARLY","PARTLY","PARTNER","PARTY","PASS","PASSAGE","PAST","PATH","PATIENT","PATTERN","PAY","PAYMENT","PEACE","PENSION","PEOPLE","PER","PERCENT","PERFECT","PERFORM","PERFORMANCE","PERHAPS","PERIOD","PERMANENT","PERSON","PERSONAL","PERSUADE","PHASE","PHONE","PHOTOGRAPH","PHYSICAL","PICK","PICTURE","PIECE","PLACE","PLAN","PLANNING","PLANT","PLASTIC","PLATE","PLAY","PLAYER","PLEASE","PLEASURE","PLENTY","PLUS","POCKET","POINT","POLICE","POLICY","POLITICAL","POLITICS","POOL","POOR","POPULAR","POPULATION","POSITION","POSITIVE","POSSIBILITY","POSSIBLE","POSSIBLY","POST","POTENTIAL","POUND","POWER","POWERFUL","PRACTICAL","PRACTICE","PREFER","PREPARE","PRESENCE","PRESENT","PRESIDENT","PRESS","PRESSURE","PRETTY","PREVENT","PREVIOUS","PREVIOUSLY","PRICE","PRIMARY","PRIME","PRINCIPLE","PRIORITY","PRISON","PRISONER","PRIVATE","PROBABLY","PROBLEM","PROCEDURE","PROCESS","PRODUCE","PRODUCT","PRODUCTION","PROFESSIONAL","PROFIT","PROGRAM","PROGRAMME","PROGRESS","PROJECT","PROMISE","PROMOTE","PROPER","PROPERLY","PROPERTY","PROPORTION","PROPOSE","PROPOSAL","PROSPECT","PROTECT","PROTECTION","PROVE","PROVIDE","PROVIDED","PROVISION","PUB","PUBLIC","PUBLICATION","PUBLISH","PULL","PUPIL","PURPOSE","PUSH","PUT","QUALITY","QUARTER","QUESTION","QUICK","QUICKLY","QUIET","QUITE","RACE","RADIO","RAILWAY","RAIN","RAISE","RANGE","RAPIDLY","RARE","RATE","RATHER","REACH","REACTION","READ","READER","READING","READY","REAL","REALISE","REALITY","REALIZE","REALLY","REASON","REASONABLE","RECALL","RECEIVE","RECENT","RECENTLY","RECOGNISE","RECOGNITION","RECOGNIZE","RECOMMEND","RECORD","RECOVER","RED","REDUCE","REDUCTION","REFER","REFERENCE","REFLECT","REFORM","REFUSE","REGARD","REGION","REGIONAL","REGULAR","REGULATION","REJECT","RELATE","RELATION","RELATIONSHIP","RELATIVE","RELATIVELY","RELEASE","RELEVANT","RELIEF","RELIGION","RELIGIOUS","RELY","REMAIN","REMEMBER","REMIND","REMOVE","REPEAT","REPLACE","REPLY","REPORT","REPRESENT","REPRESENTATION","REPRESENTATIVE","REQUEST","REQUIRE","REQUIREMENT","RESEARCH","RESOURCE","RESPECT","RESPOND","RESPONSE","RESPONSIBILITY","RESPONSIBLE","REST","RESTAURANT","RESULT","RETAIN","RETURN","REVEAL","REVENUE","REVIEW","REVOLUTION","RICH","RIDE","RIGHT","RING","RISE","RISK","RIVER","ROAD","ROCK","ROLE","ROLL","ROOF","ROOM","ROUND","ROUTE","ROW","ROYAL","RULE","RUN","RURAL","SAFE","SAFETY","SALE","SAME","SAMPLE","SATISFY","SAVE","SAY","SCALE","SCENE","SCHEME","SCHOOL","SCIENCE","SCIENTIFIC","SCIENTIST","SCORE","SCREEN","SEA","SEARCH","SEASON","SEAT","SECOND","SECONDARY","SECRETARY","SECTION","SECTOR","SECURE","SECURITY","SEE","SEEK","SEEM","SELECT","SELECTION","SELL","SEND","SENIOR","SENSE","SENTENCE","SEPARATE","SEQUENCE","SERIES","SERIOUS","SERIOUSLY","SERVANT","SERVE","SERVICE","SESSION","SET","SETTLE","SETTLEMENT","SEVERAL","SEVERE","SEX","SEXUAL","SHAKE","SHALL","SHAPE","SHARE","SHE","SHEET","SHIP","SHOE","SHOOT","SHOP","SHORT","SHOT","SHOULD","SHOULDER","SHOUT","SHOW","SHUT","SIDE","SIGHT","SIGN","SIGNAL","SIGNIFICANCE","SIGNIFICANT","SILENCE","SIMILAR","SIMPLE","SIMPLY","SINCE","SING","SINGLE","SIR","SISTER","SIT","SITE","SITUATION","SIZE","SKILL","SKIN","SKY","SLEEP","SLIGHTLY","SLIP","SLOW","SLOWLY","SMALL","SMILE","SO","SOCIAL","SOCIETY","SOFT","SOFTWARE","SOIL","SOLDIER","SOLICITOR","SOLUTION","SOME","SOMEBODY","SOMEONE","SOMETHING","SOMETIMES","SOMEWHAT","SOMEWHERE","SON","SONG","SOON","SORRY","SORT","SOUND","SOURCE","SOUTH","SOUTHERN","SPACE","SPEAK","SPEAKER","SPECIAL","SPECIES","SPECIFIC","SPEECH","SPEED","SPEND","SPIRIT","SPORT","SPOT","SPREAD","SPRING","STAFF","STAGE","STAND","STANDARD","STAR","START","STATE","STATEMENT","STATION","STATUS","STAY","STEAL","STEP","STICK","STILL","STOCK","STONE","STOP","STORE","STORY","STRAIGHT","STRANGE","STRATEGY","STREET","STRENGTH","STRIKE","STRONG","STRONGLY","STRUCTURE","STUDENT","STUDIO","STUDY","STUFF","STYLE","SUBJECT","SUBSTANTIAL","SUCCEED","SUCCESS","SUCCESSFUL","SUCH","SUDDENLY","SUFFER","SUFFICIENT","SUGGEST","SUGGESTION","SUITABLE","SUM","SUMMER","SUN","SUPPLY","SUPPORT","SUPPOSE","SURE","SURELY","SURFACE","SURPRISE","SURROUND","SURVEY","SURVIVE","SWITCH","SYSTEM","TABLE","TAKE","TALK","TALL","TAPE","TARGET","TASK","TAX","TEA","TEACH","TEACHER","TEACHING","TEAM","TEAR","TECHNICAL","TECHNIQUE","TECHNOLOGY","TELEPHONE","TELEVISION","TELL","TEMPERATURE","TEND","TERM","TERMS","TERRIBLE","TEST","TEXT","THAN","THANK","THANKS","THAT","THE","THEATRE","THEIR","THEM","THEME","THEMSELVES","THEN","THEORY","THERE","THEREFORE","THESE","THEY","THIN","THING","THINK","THIS","THOSE","THOUGH","THOUGHT","THREAT","THREATEN","THROUGH","THROUGHOUT","THROW","THUS","TICKET","TIME","TINY","TITLE","TO","TODAY","TOGETHER","TOMORROW","TONE","TONIGHT","TOO","TOOL","TOOTH","TOP","TOTAL","TOTALLY","TOUCH","TOUR","TOWARDS","TOWN","TRACK","TRADE","TRADITION","TRADITIONAL","TRAFFIC","TRAIN","TRAINING","TRANSFER","TRANSPORT","TRAVEL","TREAT","TREATMENT","TREATY","TREE","TREND","TRIAL","TRIP","TROOP","TROUBLE","TRUE","TRUST","TRUTH","TRY","TURN","TWICE","TYPE","TYPICAL","UNABLE","UNDER","UNDERSTAND","UNDERSTANDING","UNDERTAKE","UNEMPLOYMENT","UNFORTUNATELY","UNION","UNIT","UNITED","UNIVERSITY","UNLESS","UNLIKELY","UNTIL","UP","UPON","UPPER","URBAN","US","USE","USED","USEFUL","USER","USUAL","USUALLY","VALUE","VARIATION","VARIETY","VARIOUS","VARY","VAST","VEHICLE","VERSION","VERY","VIA","VICTIM","VICTORY","VIDEO","VIEW","VILLAGE","VIOLENCE","VISION","VISIT","VISITOR","VITAL","VOICE","VOLUME","VOTE","WAGE","WAIT","WALK","WALL","WANT","WAR","WARM","WARN","WASH","WATCH","WATER","WAVE","WAY","WE","WEAK","WEAPON","WEAR","WEATHER","WEEK","WEEKEND","WEIGHT","WELCOME","WELFARE","WELL","WEST","WESTERN","WHAT","WHATEVER","WHEN","WHERE","WHEREAS","WHETHER","WHICH","WHILE","WHILST","WHITE","WHO","WHOLE","WHOM","WHOSE","WHY","WIDE","WIDELY","WIFE","WILD","WILL","WIN","WIND","WINDOW","WINE","WING","WINNER","WINTER","WISH","WITH","WITHDRAW","WITHIN","WITHOUT","WOMAN","WONDER","WONDERFUL","WOOD","WORD","WORK","WORKER","WORKING","WORKS","WORLD","WORRY","WORTH","WOULD","WRITE","WRITER","WRITING","WRONG","YARD","YEAH","YEAR","YES","YESTERDAY","YET","YOU","YOUNG","YOUR","YOURSELF","YOUTH"
+];
+```
+
+## --seed-contents--
+
+```js
+function anagramicSquares(words) {
+
+ return true;
+}
+
+// Only change code above this line
+const testWords1 = [
+"DAMAGE","DANGER","DANGEROUS","DARK","DATA","DATE","DAUGHTER","DAY","DEAD","DEAL","DEATH","DEBATE","DEBT","DECADE","DECIDE","DECISION","DECLARE","DEEP","DEFENCE","DEFENDANT","DEFINE","DEFINITION","DEGREE","DELIVER","DEMAND","DEMOCRATIC","DEMONSTRATE","DENY","DEPARTMENT","DEPEND","DEPUTY","DERIVE","DESCRIBE","DESCRIPTION","DESIGN","DESIRE","DESK","DESPITE","DESTROY","DETAIL","DETAILED","DETERMINE","DEVELOP","DEVELOPMENT","DEVICE","DIE","DIFFERENCE","DIFFERENT","DIFFICULT","DIFFICULTY","DINNER","DIRECT","DIRECTION","DIRECTLY","DIRECTOR","DISAPPEAR","DISCIPLINE","DISCOVER","DISCUSS","DISCUSSION","DISEASE","DISPLAY","DISTANCE","DISTINCTION","DISTRIBUTION","DISTRICT","DIVIDE","DIVISION","DO","DOCTOR","DOCUMENT","DOG","DOMESTIC","DOOR","DOUBLE","DOUBT","DOWN","DRAW","DRAWING","DREAM","DRESS","DRINK","DRIVE","DRIVER","DROP","DRUG","DRY","DUE","DURING","DUTY","LABOUR","LACK","LADY","LAND","LANGUAGE","LARGE","LARGELY","LAST","LATE","LATER","LATTER","LAUGH","LAUNCH","LAW","LAWYER","LAY","LEAD","LEADER","LEADERSHIP","LEADING","LEAF","LEAGUE","LEAN","LEARN","LEAST","LEAVE","LEFT","LEG","LEGAL","LEGISLATION","LENGTH","LESS","LET","LETTER","LEVEL","LIABILITY","LIBERAL","LIBRARY","LIE","LIFE","LIFT","LIGHT","LIKE","LIKELY","LIMIT","LIMITED","LINE","LINK","LIP","LIST","LISTEN","LITERATURE","LITTLE","LIVE","LIVING","LOAN","LOCAL","LOCATION","LONG","LOOK","LORD","LOSE","LOSS","LOT","LOVE","LOVELY","LOW","LUNCH"
+];
+
+anagramicSquares(testWords1);
+```
+
+# --solutions--
+
+```js
+function anagramicSquares(words) {
+ // Based on https://www.mathblog.dk/project-euler-98-anagrams-square-numbers/
+ function findMaximumSquare(squares, word1, word2) {
+ let maximumSquare = 0;
+
+ for (let i = 0; i < squares.length; i++) {
+ const length = squares[i].toString().length;
+
+ if (length < word1.length) {
+ continue;
+ }
+ if (length > word1.length) {
+ break;
+ }
+
+ const word1Square = squares[i];
+ const letterToDigit = mapLettersToDigits(word1, word1Square);
+
+ const noProperMappingExist = Object.keys(letterToDigit).length === 0;
+ if (noProperMappingExist) {
+ continue;
+ }
+
+ const word2Square = getNumberFromMapping(word2, letterToDigit);
+ if (word2Square === 0) {
+ continue;
+ }
+
+ const doesWord2SquareExist = squares.indexOf(word2Square) !== -1;
+ if (doesWord2SquareExist) {
+ const pairMaximum = Math.max(word1Square, word2Square);
+ maximumSquare = Math.max(maximumSquare, pairMaximum);
+ }
+ }
+ return maximumSquare;
+ }
+
+ function getNumberFromMapping(word, letterToDigit) {
+ const wouldNumberHaveLeadingZero = letterToDigit[word[0]] === 0;
+ if (wouldNumberHaveLeadingZero) {
+ return 0;
+ }
+
+ let number = 0;
+ for (let i = 0; i < word.length; i++) {
+ number = number * 10 + letterToDigit[word[i]];
+ }
+ return number;
+ }
+
+ function mapLettersToDigits(word, square) {
+ const letterToDigit = {};
+ for (let j = word.length - 1; j >= 0; j--) {
+ const curDigit = square % 10;
+ square = Math.floor(square / 10);
+
+ const curLetter = word[j];
+
+ const isLetterRepeated = letterToDigit.hasOwnProperty(curLetter);
+ if (isLetterRepeated) {
+ const isLetterUsedForTheSameDigit =
+ letterToDigit[curLetter] === curDigit;
+ if (isLetterUsedForTheSameDigit) {
+ continue;
+ }
+
+ return {};
+ }
+
+ const isDigitUsed = Object.values(letterToDigit).indexOf(curDigit) !== -1;
+ if (isDigitUsed) {
+ return {};
+ }
+
+ letterToDigit[curLetter] = curDigit;
+ }
+ return letterToDigit;
+ }
+
+ function groupWordsWithSameLetters(words) {
+ const lettersToWords = {};
+ for (let i = 0; i < words.length; i++) {
+ const word = words[i];
+ const sortedLetters = word.split('').sort().join('');
+ if (!lettersToWords.hasOwnProperty(sortedLetters)) {
+ lettersToWords[sortedLetters] = [];
+ }
+ lettersToWords[sortedLetters].push(word);
+ }
+ return lettersToWords;
+ }
+
+ const lettersToWords = groupWordsWithSameLetters(words);
+
+ const anagrams = Object.keys(lettersToWords).filter(
+ letters => lettersToWords[letters].length > 1
+ );
+ const lengthOfLongestAnagram = anagrams
+ .map(anagram => anagram.length)
+ .sort((a, b) => b - a)[0];
+
+ const squares = [];
+ const numberLimit = (10 ** lengthOfLongestAnagram) ** 0.5;
+ for (let number = 2; number < numberLimit; number++) {
+ const square = number ** 2;
+ squares.push(square);
+ }
+
+ let largestSquare = 0;
+ for (let i = 0; i < anagrams.length; i++) {
+ const curWords = lettersToWords[anagrams[i]];
+
+ for (let j = 0; j < curWords.length; j++) {
+ for (let k = j + 1; k < curWords.length; k++) {
+ const squareValue = findMaximumSquare(
+ squares,
+ curWords[j],
+ curWords[k]
+ );
+ if (squareValue > largestSquare) {
+ largestSquare = squareValue;
+ }
+ }
+ }
+ }
+
+ return largestSquare;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-99-largest-exponential.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-99-largest-exponential.md
new file mode 100644
index 00000000000..af44a7d0bd7
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-1-to-100/problem-99-largest-exponential.md
@@ -0,0 +1,83 @@
+---
+id: 5900f3d01000cf542c50fee2
+title: 'Problem 99: Largest exponential'
+challengeType: 1
+forumTopicId: 302216
+dashedName: problem-99-largest-exponential
+---
+
+# --description--
+
+Comparing two numbers written in index form like $2^{11}$ and $3^7$ is not difficult, as any calculator would confirm that $2^{11} = 2048 < 3^7 = 2187$.
+
+However, confirming that $632382^{518061} < 519432^{525806}$ would be much more difficult, as both numbers contain over three million digits.
+
+Using the 2D `baseExp` array of base/exponent pairs, determine pair with the greatest numerical value and return it.
+
+# --hints--
+
+`largestExponential(testArray1)` should return an array.
+
+```js
+assert(Array.isArray(largestExponential(_testArray1)));
+```
+
+`largestExponential(testArray1)` should return `[840237, 507276]`.
+
+```js
+assert.deepEqual(largestExponential(_testArray1), [840237, 507276]);
+```
+
+`largestExponential(testArray2)` should return `[895447, 504922]`.
+
+```js
+assert.deepEqual(largestExponential(_testArray2), [895447, 504922]);
+```
+
+# --seed--
+
+## --after-user-code--
+
+```js
+const _testArray1 = [
+ [492798,527927],[30125,670983],[895603,504906],[450785,531539],[840237,507276],[380711,538522],[63577,625673],[76801,615157],[502694,527123]
+];
+const _testArray2 = [
+ [519432,525806],[632382,518061],[78864,613712],[466580,530130],[780495,510032],[525895,525320],[15991,714883],[960290,502358],[760018,511029],[166800,575487],[210884,564478],[555151,523163],[681146,515199],[563395,522587],[738250,512126],[923525,503780],[595148,520429],[177108,572629],[750923,511482],[440902,532446],[881418,505504],[422489,534197],[979858,501616],[685893,514935],[747477,511661],[167214,575367],[234140,559696],[940238,503122],[728969,512609],[232083,560102],[900971,504694],[688801,514772],[189664,569402],[891022,505104],[445689,531996],[119570,591871],[821453,508118],[371084,539600],[911745,504251],[623655,518600],[144361,582486],[352442,541775],[420726,534367],[295298,549387],[6530,787777],[468397,529976],[672336,515696],[431861,533289],[84228,610150],[805376,508857],[444409,532117],[33833,663511],[381850,538396],[402931,536157],[92901,604930],[304825,548004],[731917,512452],[753734,511344],[51894,637373],[151578,580103],[295075,549421],[303590,548183],[333594,544123],[683952,515042],[60090,628880],[951420,502692],[28335,674991],[714940,513349],[343858,542826],[549279,523586],[804571,508887],[260653,554881],[291399,549966],[402342,536213],[408889,535550],[40328,652524],[375856,539061],[768907,510590],[165993,575715],[976327,501755],[898500,504795],[360404,540830],[478714,529095],[694144,514472],[488726,528258],[841380,507226],[328012,544839],[22389,690868],[604053,519852],[329514,544641],[772965,510390],[492798,527927],[30125,670983],[895603,504906],[450785,531539],[840237,507276],[380711,538522],[63577,625673],[76801,615157],[502694,527123],[597706,520257],[310484,547206],[944468,502959],[121283,591152],[451131,531507],[566499,522367],[425373,533918],[40240,652665],[39130,654392],[714926,513355],[469219,529903],[806929,508783],[287970,550487],[92189,605332],[103841,599094],[671839,515725],[452048,531421],[987837,501323],[935192,503321],[88585,607450],[613883,519216],[144551,582413],[647359,517155],[213902,563816],[184120,570789],[258126,555322],[502546,527130],[407655,535678],[401528,536306],[477490,529193],[841085,507237],[732831,512408],[833000,507595],[904694,504542],[581435,521348],[455545,531110],[873558,505829],[94916,603796],[720176,513068],[545034,523891],[246348,557409],[556452,523079],[832015,507634],[173663,573564],[502634,527125],[250732,556611],[569786,522139],[216919,563178],[521815,525623],[92304,605270],[164446,576167],[753413,511364],[11410,740712],[448845,531712],[925072,503725],[564888,522477],[7062,780812],[641155,517535],[738878,512100],[636204,517828],[372540,539436],[443162,532237],[571192,522042],[655350,516680],[299741,548735],[581914,521307],[965471,502156],[513441,526277],[808682,508700],[237589,559034],[543300,524025],[804712,508889],[247511,557192],[543486,524008],[504383,526992],[326529,545039],[792493,509458],[86033,609017],[126554,589005],[579379,521481],[948026,502823],[404777,535969],[265767,554022],[266876,553840],[46631,643714],[492397,527958],[856106,506581],[795757,509305],[748946,511584],[294694,549480],[409781,535463],[775887,510253],[543747,523991],[210592,564536],[517119,525990],[520253,525751],[247926,557124],[592141,520626],[346580,542492],[544969,523902],[506501,526817],[244520,557738],[144745,582349],[69274,620858],[292620,549784],[926027,503687],[736320,512225],[515528,526113],[407549,535688],[848089,506927],[24141,685711],[9224,757964],[980684,501586],[175259,573121],[489160,528216],[878970,505604],[969546,502002],[525207,525365],[690461,514675],[156510,578551],[659778,516426],[468739,529945],[765252,510770],[76703,615230],[165151,575959],[29779,671736],[928865,503569],[577538,521605],[927555,503618],[185377,570477],[974756,501809],[800130,509093],[217016,563153],[365709,540216],[774508,510320],[588716,520851],[631673,518104],[954076,502590],[777828,510161],[990659,501222],[597799,520254],[786905,509727],[512547,526348],[756449,511212],[869787,505988],[653747,516779],[84623,609900],[839698,507295],[30159,670909],[797275,509234],[678136,515373],[897144,504851],[989554,501263],[413292,535106],[55297,633667],[788650,509637],[486748,528417],[150724,580377],[56434,632490],[77207,614869],[588631,520859],[611619,519367],[100006,601055],[528924,525093],[190225,569257],[851155,506789],[682593,515114],[613043,519275],[514673,526183],[877634,505655],[878905,505602],[1926,914951],[613245,519259],[152481,579816],[841774,507203],[71060,619442],[865335,506175],[90244,606469],[302156,548388],[399059,536557],[478465,529113],[558601,522925],[69132,620966],[267663,553700],[988276,501310],[378354,538787],[529909,525014],[161733,576968],[758541,511109],[823425,508024],[149821,580667],[269258,553438],[481152,528891],[120871,591322],[972322,501901],[981350,501567],[676129,515483],[950860,502717],[119000,592114],[392252,537272],[191618,568919],[946699,502874],[289555,550247],[799322,509139],[703886,513942],[194812,568143],[261823,554685],[203052,566221],[217330,563093],[734748,512313],[391759,537328],[807052,508777],[564467,522510],[59186,629748],[113447,594545],[518063,525916],[905944,504492],[613922,519213],[439093,532607],[445946,531981],[230530,560399],[297887,549007],[459029,530797],[403692,536075],[855118,506616],[963127,502245],[841711,507208],[407411,535699],[924729,503735],[914823,504132],[333725,544101],[176345,572832],[912507,504225],[411273,535308],[259774,555036],[632853,518038],[119723,591801],[163902,576321],[22691,689944],[402427,536212],[175769,572988],[837260,507402],[603432,519893],[313679,546767],[538165,524394],[549026,523608],[61083,627945],[898345,504798],[992556,501153],[369999,539727],[32847,665404],[891292,505088],[152715,579732],[824104,507997],[234057,559711],[730507,512532],[960529,502340],[388395,537687],[958170,502437],[57105,631806],[186025,570311],[993043,501133],[576770,521664],[215319,563513],[927342,503628],[521353,525666],[39563,653705],[752516,511408],[110755,595770],[309749,547305],[374379,539224],[919184,503952],[990652,501226],[647780,517135],[187177,570017],[168938,574877],[649558,517023],[278126,552016],[162039,576868],[658512,516499],[498115,527486],[896583,504868],[561170,522740],[747772,511647],[775093,510294],[652081,516882],[724905,512824],[499707,527365],[47388,642755],[646668,517204],[571700,522007],[180430,571747],[710015,513617],[435522,532941],[98137,602041],[759176,511070],[486124,528467],[526942,525236],[878921,505604],[408313,535602],[926980,503640],[882353,505459],[566887,522345],[3326,853312],[911981,504248],[416309,534800],[392991,537199],[622829,518651],[148647,581055],[496483,527624],[666314,516044],[48562,641293],[672618,515684],[443676,532187],[274065,552661],[265386,554079],[347668,542358],[31816,667448],[181575,571446],[961289,502320],[365689,540214],[987950,501317],[932299,503440],[27388,677243],[746701,511701],[492258,527969],[147823,581323],[57918,630985],[838849,507333],[678038,515375],[27852,676130],[850241,506828],[818403,508253],[131717,587014],[850216,506834],[904848,504529],[189758,569380],[392845,537217],[470876,529761],[925353,503711],[285431,550877],[454098,531234],[823910,508003],[318493,546112],[766067,510730],[261277,554775],[421530,534289],[694130,514478],[120439,591498],[213308,563949],[854063,506662],[365255,540263],[165437,575872],[662240,516281],[289970,550181],[847977,506933],[546083,523816],[413252,535113],[975829,501767],[361540,540701],[235522,559435],[224643,561577],[736350,512229],[328303,544808],[35022,661330],[307838,547578],[474366,529458],[873755,505819],[73978,617220],[827387,507845],[670830,515791],[326511,545034],[309909,547285],[400970,536363],[884827,505352],[718307,513175],[28462,674699],[599384,520150],[253565,556111],[284009,551093],[343403,542876],[446557,531921],[992372,501160],[961601,502308],[696629,514342],[919537,503945],[894709,504944],[892201,505051],[358160,541097],[448503,531745],[832156,507636],[920045,503924],[926137,503675],[416754,534757],[254422,555966],[92498,605151],[826833,507873],[660716,516371],[689335,514746],[160045,577467],[814642,508425],[969939,501993],[242856,558047],[76302,615517],[472083,529653],[587101,520964],[99066,601543],[498005,527503],[709800,513624],[708000,513716],[20171,698134],[285020,550936],[266564,553891],[981563,501557],[846502,506991],[334,1190800],[209268,564829],[9844,752610],[996519,501007],[410059,535426],[432931,533188],[848012,506929],[966803,502110],[983434,501486],[160700,577267],[504374,526989],[832061,507640],[392825,537214],[443842,532165],[440352,532492],[745125,511776],[13718,726392],[661753,516312],[70500,619875],[436952,532814],[424724,533973],[21954,692224],[262490,554567],[716622,513264],[907584,504425],[60086,628882],[837123,507412],[971345,501940],[947162,502855],[139920,584021],[68330,621624],[666452,516038],[731446,512481],[953350,502619],[183157,571042],[845400,507045],[651548,516910],[20399,697344],[861779,506331],[629771,518229],[801706,509026],[189207,569512],[737501,512168],[719272,513115],[479285,529045],[136046,585401],[896746,504860],[891735,505067],[684771,514999],[865309,506184],[379066,538702],[503117,527090],[621780,518717],[209518,564775],[677135,515423],[987500,501340],[197049,567613],[329315,544673],[236756,559196],[357092,541226],[520440,525733],[213471,563911],[956852,502490],[702223,514032],[404943,535955],[178880,572152],[689477,514734],[691351,514630],[866669,506128],[370561,539656],[739805,512051],[71060,619441],[624861,518534],[261660,554714],[366137,540160],[166054,575698],[601878,519990],[153445,579501],[279899,551729],[379166,538691],[423209,534125],[675310,515526],[145641,582050],[691353,514627],[917468,504026],[284778,550976],[81040,612235],[161699,576978],[616394,519057],[767490,510661],[156896,578431],[427408,533714],[254849,555884],[737217,512182],[897133,504851],[203815,566051],[270822,553189],[135854,585475],[778805,510111],[784373,509847],[305426,547921],[733418,512375],[732087,512448],[540668,524215],[702898,513996],[628057,518328],[640280,517587],[422405,534204],[10604,746569],[746038,511733],[839808,507293],[457417,530938],[479030,529064],[341758,543090],[620223,518824],[251661,556451],[561790,522696],[497733,527521],[724201,512863],[489217,528217],[415623,534867],[624610,518548],[847541,506953],[432295,533249],[400391,536421],[961158,502319],[139173,584284],[421225,534315],[579083,521501],[74274,617000],[701142,514087],[374465,539219],[217814,562985],[358972,540995],[88629,607424],[288597,550389],[285819,550812],[538400,524385],[809930,508645],[738326,512126],[955461,502535],[163829,576343],[826475,507891],[376488,538987],[102234,599905],[114650,594002],[52815,636341],[434037,533082],[804744,508880],[98385,601905],[856620,506559],[220057,562517],[844734,507078],[150677,580387],[558697,522917],[621751,518719],[207067,565321],[135297,585677],[932968,503404],[604456,519822],[579728,521462],[244138,557813],[706487,513800],[711627,513523],[853833,506674],[497220,527562],[59428,629511],[564845,522486],[623621,518603],[242689,558077],[125091,589591],[363819,540432],[686453,514901],[656813,516594],[489901,528155],[386380,537905],[542819,524052],[243987,557841],[693412,514514],[488484,528271],[896331,504881],[336730,543721],[728298,512647],[604215,519840],[153729,579413],[595687,520398],[540360,524240],[245779,557511],[924873,503730],[509628,526577],[528523,525122],[3509,847707],[522756,525555],[895447,504922],[44840,646067],[45860,644715],[463487,530404],[398164,536654],[894483,504959],[619415,518874],[966306,502129],[990922,501212],[835756,507474],[548881,523618],[453578,531282],[474993,529410],[80085,612879],[737091,512193],[50789,638638],[979768,501620],[792018,509483],[665001,516122],[86552,608694],[462772,530469],[589233,520821],[891694,505072],[592605,520594],[209645,564741],[42531,649269],[554376,523226],[803814,508929],[334157,544042],[175836,572970],[868379,506051],[658166,516520],[278203,551995],[966198,502126],[627162,518387],[296774,549165],[311803,547027],[843797,507118],[702304,514032],[563875,522553],[33103,664910],[191932,568841],[543514,524006],[506835,526794],[868368,506052],[847025,506971],[678623,515342],[876139,505726],[571997,521984],[598632,520198],[213590,563892],[625404,518497],[726508,512738],[689426,514738],[332495,544264],[411366,535302],[242546,558110],[315209,546555],[797544,509219],[93889,604371],[858879,506454],[124906,589666],[449072,531693],[235960,559345],[642403,517454],[720567,513047],[705534,513858],[603692,519870],[488137,528302],[157370,578285],[63515,625730],[666326,516041],[619226,518883],[443613,532186],[597717,520257],[96225,603069],[86940,608450],[40725,651929],[460976,530625],[268875,553508],[270671,553214],[363254,540500],[384248,538137],[762889,510892],[377941,538833],[278878,551890],[176615,572755],[860008,506412],[944392,502967],[608395,519571],[225283,561450],[45095,645728],[333798,544090],[625733,518476],[995584,501037],[506135,526853],[238050,558952],[557943,522972],[530978,524938],[634244,517949],[177168,572616],[85200,609541],[953043,502630],[523661,525484],[999295,500902],[840803,507246],[961490,502312],[471747,529685],[380705,538523],[911180,504275],[334149,544046],[478992,529065],[325789,545133],[335884,543826],[426976,533760],[749007,511582],[667067,516000],[607586,519623],[674054,515599],[188534,569675],[565185,522464],[172090,573988],[87592,608052],[907432,504424],[8912,760841],[928318,503590],[757917,511138],[718693,513153],[315141,546566],[728326,512645],[353492,541647],[638429,517695],[628892,518280],[877286,505672],[620895,518778],[385878,537959],[423311,534113],[633501,517997],[884833,505360],[883402,505416],[999665,500894],[708395,513697],[548142,523667],[756491,511205],[987352,501340],[766520,510705],[591775,520647],[833758,507563],[843890,507108],[925551,503698],[74816,616598],[646942,517187],[354923,541481],[256291,555638],[634470,517942],[930904,503494],[134221,586071],[282663,551304],[986070,501394],[123636,590176],[123678,590164],[481717,528841],[423076,534137],[866246,506145],[93313,604697],[783632,509880],[317066,546304],[502977,527103],[141272,583545],[71708,618938],[617748,518975],[581190,521362],[193824,568382],[682368,515131],[352956,541712],[351375,541905],[505362,526909],[905165,504518],[128645,588188],[267143,553787],[158409,577965],[482776,528754],[628896,518282],[485233,528547],[563606,522574],[111001,595655],[115920,593445],[365510,540237],[959724,502374],[938763,503184],[930044,503520],[970959,501956],[913658,504176],[68117,621790],[989729,501253],[567697,522288],[820427,508163],[54236,634794],[291557,549938],[124961,589646],[403177,536130],[405421,535899],[410233,535417],[815111,508403],[213176,563974],[83099,610879],[998588,500934],[513640,526263],[129817,587733],[1820,921851],[287584,550539],[299160,548820],[860621,506386],[529258,525059],[586297,521017],[953406,502616],[441234,532410],[986217,501386],[781938,509957],[461247,530595],[735424,512277],[146623,581722],[839838,507288],[510667,526494],[935085,503327],[737523,512167],[303455,548204],[992779,501145],[60240,628739],[939095,503174],[794368,509370],[501825,527189],[459028,530798],[884641,505363],[512287,526364],[835165,507499],[307723,547590],[160587,577304],[735043,512300],[493289,527887],[110717,595785],[306480,547772],[318593,546089],[179810,571911],[200531,566799],[314999,546580],[197020,567622],[301465,548487],[237808,559000],[131944,586923],[882527,505449],[468117,530003],[711319,513541],[156240,578628],[965452,502162],[992756,501148],[437959,532715],[739938,512046],[614249,519196],[391496,537356],[62746,626418],[688215,514806],[75501,616091],[883573,505412],[558824,522910],[759371,511061],[173913,573489],[891351,505089],[727464,512693],[164833,576051],[812317,508529],[540320,524243],[698061,514257],[69149,620952],[471673,529694],[159092,577753],[428134,533653],[89997,606608],[711061,513557],[779403,510081],[203327,566155],[798176,509187],[667688,515963],[636120,517833],[137410,584913],[217615,563034],[556887,523038],[667229,515991],[672276,515708],[325361,545187],[172115,573985],[13846,725685]
+];
+```
+
+## --seed-contents--
+
+```js
+function largestExponential(baseExp) {
+
+ return true;
+}
+
+// Only change code above this line
+
+const testArray1 = [
+ [492798,527927],[30125,670983],[895603,504906],[450785,531539],[840237,507276],[380711,538522],[63577,625673],[76801,615157],[502694,527123]
+];
+
+largestExponential(testArray1);
+```
+
+# --solutions--
+
+```js
+function largestExponential(baseExp) {
+ let maximum = 0;
+ let indexOfMaximum = 0;
+ for (let i = 1; i < baseExp.length; i++) {
+ const curValue = Math.log(baseExp[i][0]) * baseExp[i][1];
+ if (curValue > maximum) {
+ maximum = curValue;
+ indexOfMaximum = i;
+ }
+ }
+
+ return baseExp[indexOfMaximum];
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-101-optimum-polynomial.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-101-optimum-polynomial.md
new file mode 100644
index 00000000000..803f95dc33e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-101-optimum-polynomial.md
@@ -0,0 +1,58 @@
+---
+id: 5900f3d21000cf542c50fee4
+title: 'Problem 101: Optimum polynomial'
+challengeType: 1
+forumTopicId: 301725
+dashedName: problem-101-optimum-polynomial
+---
+
+# --description--
+
+If we are presented with the first k terms of a sequence it is impossible to say with certainty the value of the next term, as there are infinitely many polynomial functions that can model the sequence.
+
+As an example, let us consider the sequence of cube numbers. This is defined by the generating function, $u_n = n^3: 1, 8, 27, 64, 125, 216, \ldots$
+
+Suppose we were only given the first two terms of this sequence. Working on the principle that "simple is best" we should assume a linear relationship and predict the next term to be 15 (common difference 7). Even if we were presented with the first three terms, by the same principle of simplicity, a quadratic relationship should be assumed.
+
+We shall define $OP(k, n)$ to be the $n^{th}$ term of the optimum polynomial generating function for the first k terms of a sequence. It should be clear that $OP(k, n)$ will accurately generate the terms of the sequence for $n ≤ k$, and potentially the first incorrect term (FIT) will be $OP(k, k+1)$; in which case we shall call it a bad OP (BOP).
+
+As a basis, if we were only given the first term of sequence, it would be most sensible to assume constancy; that is, for $n ≥ 2, OP(1, n) = u_1$.
+
+Hence we obtain the following OPs for the cubic sequence:
+
+$$\begin{array}{ll} OP(1, n) = 1 & 1, {\color{red}1}, 1, 1, \ldots \\\\
+ OP(2, n) = 7n−6 & 1, 8, {\color{red}{15}}, \ldots \\\\ OP(3, n) = 6n^2−11n+6 & 1, 8, 27, {\color{red}{58}}, \ldots \\\\
+ OP(4, n) = n^3 & 1, 8, 27, 64, 125, \ldots \end{array}$$
+
+Clearly no BOPs exist for k ≥ 4. By considering the sum of FITs generated by the BOPs (indicated in $\color{red}{red}$ above), we obtain 1 + 15 + 58 = 74. Consider the following tenth degree polynomial generating function:
+
+$$u_n = 1 − n + n^2 − n^3 + n^4 − n^5 + n^6 − n^7 + n^8 − n^9 + n^{10}$$
+
+Find the sum of FITs for the BOPs.
+
+# --hints--
+
+`optimumPolynomial()` should return `37076114526`.
+
+```js
+assert.strictEqual(optimumPolynomial(), 37076114526);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function optimumPolynomial() {
+
+ return true;
+}
+
+optimumPolynomial();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-102-triangle-containment.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-102-triangle-containment.md
new file mode 100644
index 00000000000..c90a827dda3
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-102-triangle-containment.md
@@ -0,0 +1,156 @@
+---
+id: 5900f3d21000cf542c50fee5
+title: 'Problem 102: Triangle containment'
+challengeType: 1
+forumTopicId: 301726
+dashedName: problem-102-triangle-containment
+---
+
+# --description--
+
+Three distinct points are plotted at random on a Cartesian plane, for which -1000 ≤ x, y ≤ 1000, such that a triangle is formed.
+
+Consider the following two triangles:
+
+```js
+const exampleTriangles = [
+ [[-340, 495], [-153, -910], [835, -947]],
+ [[-175, 41], [-421, -714], [574, -645]]
+];
+```
+
+It can be verified that first triangle contains the origin, whereas second triangle does not.
+
+Using the `triangles` array containing coordinates of triangles, find the number of triangles for which the interior contains the origin.
+
+# --hints--
+
+`triangleContainment(exampleTriangles)` should return a number.
+
+```js
+assert(typeof triangleContainment(_exampleTriangles) === 'number');
+```
+
+`triangleContainment(exampleTriangles)` should return `1`.
+
+```js
+assert.strictEqual(triangleContainment(_exampleTriangles), 1);
+```
+
+`triangleContainment(testTriangles1)` should return `19`.
+
+```js
+assert.strictEqual(triangleContainment(_testTriangles1), 19);
+```
+
+`triangleContainment(testTriangles2)` should return `228`.
+
+```js
+assert.strictEqual(triangleContainment(_testTriangles2), 228);
+```
+
+# --seed--
+
+## --after-user-code--
+
+```js
+const _exampleTriangles = [
+ [[-340, 495], [-153, -910], [835, -947]],
+ [[-175, 41], [-421, -714], [574, -645]]
+];
+const _testTriangles1 = [
+ [[-866,121],[-928,358],[459,-843]],[[-568,-631],[-352,-580],[-349,189]],[[-737,849],[-963,-486],[-662,970]],[[135,334],[-967,-71],[-365,-792]],[[789,21],[-227,51],[990,-275]],[[240,412],[-886,230],[591,256]],[[-609,472],[-853,-754],[959,661]],[[401,521],[521,314],[929,982]],[[-499,784],[-208,71],[-302,296]],[[-557,-948],[-553,-526],[-864,793]],[[270,-626],[828,44],[37,14]],[[-412,224],[617,-593],[502,699]],[[41,-908],[81,562],[-849,163]],[[165,917],[761,-197],[331,-341]],[[-687,314],[799,755],[-969,648]],[[-164,25],[578,439],[-334,-576]],[[213,535],[874,-177],[-551,24]],[[-689,291],[-795,-225],[-496,-125]],[[465,461],[558,-118],[-568,-909]],[[567,660],[-810,46],[-485,878]],[[-147,606],[685,-690],[-774,984]],[[568,-886],[-43,854],[-738,616]],[[-800,386],[-614,585],[764,-226]],[[-518,23],[-225,-732],[-79,440]],[[-173,-291],[-689,636],[642,-447]],[[-598,-16],[227,410],[496,211]],[[-474,-930],[-656,-321],[-420,36]],[[-435,165],[-819,555],[540,144]],[[-969,149],[828,568],[394,648]],[[65,-848],[257,720],[-625,-851]],[[981,899],[275,635],[465,-877]],[[80,290],[792,760],[-191,-321]],[[-605,-858],[594,33],[706,593]],[[585,-472],[318,-35],[354,-927]],[[-365,664],[803,581],[-965,-814]],[[-427,-238],[-480,146],[-55,-606]],[[879,-193],[250,-890],[336,117]],[[-226,-322],[-286,-765],[-836,-218]],[[-913,564],[-667,-698],[937,283]],[[872,-901],[810,-623],[-52,-709]],[[473,171],[717,38],[-429,-644]],[[225,824],[-219,-475],[-180,234]],[[-530,-797],[-948,238],[851,-623]],[[85,975],[-363,529],[598,28]],[[-799,166],[-804,210],[-769,851]],[[-687,-158],[885,736],[-381,-461]],[[447,592],[928,-514],[-515,-661]],[[-399,-777],[-493,80],[-544,-78]],[[-884,631],[171,-825],[-333,551]],[[191,268],[-577,676],[137,-33]],[[212,-853],[709,798],[583,-56]],[[-908,-172],[-540,-84],[-135,-56]],[[303,311],[406,-360],[-240,811]],[[798,-708],[824,59],[234,-57]],[[491,693],[-74,585],[-85,877]],[[509,-65],[-936,329],[-51,722]],[[-122,858],[-52,467],[-77,-609]],[[850,760],[547,-495],[-953,-952]],[[-460,-541],[890,910],[286,724]],[[-914,843],[-579,-983],[-387,-460]],[[989,-171],[-877,-326],[-899,458]],[[846,175],[-915,540],[-1000,-982]],[[-852,-920],[-306,496],[530,-18]],[[338,-991],[160,85],[-455,-661]],[[-186,-311],[-460,-563],[-231,-414]],[[-932,-302],[959,597],[793,748]],[[-366,-402],[-788,-279],[514,53]],[[-940,-956],[447,-956],[211,-285]],[[564,806],[-911,-914],[934,754]],[[575,-858],[-277,15],[409,-714]]
+];
+const _testTriangles2 = [
+ [[-340,495],[-153,-910],[835,-947]],[[-175,41],[-421,-714],[574,-645]],[[-547,712],[-352,579],[951,-786]],[[419,-864],[-83,650],[-399,171]],[[-429,-89],[-357,-930],[296,-29]],[[-734,-702],[823,-745],[-684,-62]],[[-971,762],[925,-776],[-663,-157]],[[162,570],[628,485],[-807,-896]],[[641,91],[-65,700],[887,759]],[[215,-496],[46,-931],[422,-30]],[[-119,359],[668,-609],[-358,-494]],[[440,929],[968,214],[760,-857]],[[-700,785],[838,29],[-216,411]],[[-770,-458],[-325,-53],[-505,633]],[[-752,-805],[349,776],[-799,687]],[[323,5],[561,-36],[919,-560]],[[-907,358],[264,320],[204,274]],[[-728,-466],[350,969],[292,-345]],[[940,836],[272,-533],[748,185]],[[411,998],[813,520],[316,-949]],[[-152,326],[658,-762],[148,-651]],[[330,507],[-9,-628],[101,174]],[[551,-496],[772,-541],[-702,-45]],[[-164,-489],[-90,322],[631,-59]],[[673,366],[-4,-143],[-606,-704]],[[428,-609],[801,-449],[740,-269]],[[453,-924],[-785,-346],[-853,111]],[[-738,555],[-181,467],[-426,-20]],[[958,-692],[784,-343],[505,-569]],[[620,27],[263,54],[-439,-726]],[[804,87],[998,859],[871,-78]],[[-119,-453],[-709,-292],[-115,-56]],[[-626,138],[-940,-476],[-177,-274]],[[-11,160],[142,588],[446,158]],[[538,727],[550,787],[330,810]],[[420,-689],[854,-546],[337,516]],[[872,-998],[-607,748],[473,-192]],[[653,440],[-516,-985],[808,-857]],[[374,-158],[331,-940],[-338,-641]],[[137,-925],[-179,771],[734,-715]],[[-314,198],[-115,29],[-641,-39]],[[759,-574],[-385,355],[590,-603]],[[-189,-63],[-168,204],[289,305]],[[-182,-524],[-715,-621],[911,-255]],[[331,-816],[-833,471],[168,126]],[[-514,581],[-855,-220],[-731,-507]],[[129,169],[576,651],[-87,-458]],[[783,-444],[-881,658],[-266,298]],[[603,-430],[-598,585],[368,899]],[[43,-724],[962,-376],[851,409]],[[-610,-646],[-883,-261],[-482,-881]],[[-117,-237],[978,641],[101,-747]],[[579,125],[-715,-712],[208,534]],[[672,-214],[-762,372],[874,533]],[[-564,965],[38,715],[367,242]],[[500,951],[-700,-981],[-61,-178]],[[-382,-224],[-959,903],[-282,-60]],[[-355,295],[426,-331],[-591,655]],[[892,128],[958,-271],[-993,274]],[[-454,-619],[302,138],[-790,-874]],[[-642,601],[-574,159],[-290,-318]],[[266,-109],[257,-686],[54,975]],[[162,628],[-478,840],[264,-266]],[[466,-280],[982,1],[904,-810]],[[721,839],[730,-807],[777,981]],[[-129,-430],[748,263],[943,96]],[[434,-94],[410,-990],[249,-704]],[[237,42],[122,-732],[44,-51]],[[909,-116],[-229,545],[292,717]],[[824,-768],[-807,-370],[-262,30]],[[675,58],[332,-890],[-651,791]],[[363,825],[-717,254],[684,240]],[[405,-715],[900,166],[-589,422]],[[-476,686],[-830,-319],[634,-807]],[[633,837],[-971,917],[-764,207]],[[-116,-44],[-193,-70],[908,809]],[[-26,-252],[998,408],[70,-713]],[[-601,645],[-462,842],[-644,-591]],[[-160,653],[274,113],[-138,687]],[[369,-273],[-181,925],[-167,-693]],[[-338,135],[480,-967],[-13,-840]],[[-90,-270],[-564,695],[161,907]],[[607,-430],[869,-713],[461,-469]],[[919,-165],[-776,522],[606,-708]],[[-203,465],[288,207],[-339,-458]],[[-453,-534],[-715,975],[838,-677]],[[-973,310],[-350,934],[546,-805]],[[-835,385],[708,-337],[-594,-772]],[[-14,914],[900,-495],[-627,594]],[[833,-713],[-213,578],[-296,699]],[[-27,-748],[484,455],[915,291]],[[270,889],[739,-57],[442,-516]],[[119,811],[-679,905],[184,130]],[[-678,-469],[925,553],[612,482]],[[101,-571],[-732,-842],[644,588]],[[-71,-737],[566,616],[957,-663]],[[-634,-356],[90,-207],[936,622]],[[598,443],[964,-895],[-58,529]],[[847,-467],[929,-742],[91,10]],[[-633,829],[-780,-408],[222,-30]],[[-818,57],[275,-38],[-746,198]],[[-722,-825],[-549,597],[-391,99]],[[-570,908],[430,873],[-103,-360]],[[342,-681],[512,434],[542,-528]],[[297,850],[479,609],[543,-357]],[[9,784],[212,548],[56,859]],[[-152,560],[-240,-969],[-18,713]],[[140,-133],[34,-635],[250,-163]],[[-272,-22],[-169,-662],[989,-604]],[[471,-765],[355,633],[-742,-118]],[[-118,146],[942,663],[547,-376]],[[583,16],[162,264],[715,-33]],[[-230,-446],[997,-838],[561,555]],[[372,397],[-729,-318],[-276,649]],[[92,982],[-970,-390],[-922,922]],[[-981,713],[-951,-337],[-669,670]],[[-999,846],[-831,-504],[7,-128]],[[455,-954],[-370,682],[-510,45]],[[822,-960],[-892,-385],[-662,314]],[[-668,-686],[-367,-246],[530,-341]],[[-723,-720],[-926,-836],[-142,757]],[[-509,-134],[384,-221],[-873,-639]],[[-803,-52],[-706,-669],[373,-339]],[[933,578],[631,-616],[770,555]],[[741,-564],[-33,-605],[-576,275]],[[-715,445],[-233,-730],[734,-704]],[[120,-10],[-266,-685],[-490,-17]],[[-232,-326],[-457,-946],[-457,-116]],[[811,52],[639,826],[-200,147]],[[-329,279],[293,612],[943,955]],[[-721,-894],[-393,-969],[-642,453]],[[-688,-826],[-352,-75],[371,79]],[[-809,-979],[407,497],[858,-248]],[[-485,-232],[-242,-582],[-81,849]],[[141,-106],[123,-152],[806,-596]],[[-428,57],[-992,811],[-192,478]],[[864,393],[122,858],[255,-876]],[[-284,-780],[240,457],[354,-107]],[[956,605],[-477,44],[26,-678]],[[86,710],[-533,-815],[439,327]],[[-906,-626],[-834,763],[426,-48]],[[201,-150],[-904,652],[475,412]],[[-247,149],[81,-199],[-531,-148]],[[923,-76],[-353,175],[-121,-223]],[[427,-674],[453,472],[-410,585]],[[931,776],[-33,85],[-962,-865]],[[-655,-908],[-902,208],[869,792]],[[-316,-102],[-45,-436],[-222,885]],[[-309,768],[-574,653],[745,-975]],[[896,27],[-226,993],[332,198]],[[323,655],[-89,260],[240,-902]],[[501,-763],[-424,793],[813,616]],[[993,375],[-938,-621],[672,-70]],[[-880,-466],[-283,770],[-824,143]],[[63,-283],[886,-142],[879,-116]],[[-964,-50],[-521,-42],[-306,-161]],[[724,-22],[866,-871],[933,-383]],[[-344,135],[282,966],[-80,917]],[[-281,-189],[420,810],[362,-582]],[[-515,455],[-588,814],[162,332]],[[555,-436],[-123,-210],[869,-943]],[[589,577],[232,286],[-554,876]],[[-773,127],[-58,-171],[-452,125]],[[-428,575],[906,-232],[-10,-224]],[[437,276],[-335,-348],[605,878]],[[-964,511],[-386,-407],[168,-220]],[[307,513],[912,-463],[-423,-416]],[[-445,539],[273,886],[-18,760]],[[-396,-585],[-670,414],[47,364]],[[143,-506],[754,906],[-971,-203]],[[-544,472],[-180,-541],[869,-465]],[[-779,-15],[-396,890],[972,-220]],[[-430,-564],[503,182],[-119,456]],[[89,-10],[-739,399],[506,499]],[[954,162],[-810,-973],[127,870]],[[890,952],[-225,158],[828,237]],[[-868,952],[349,465],[574,750]],[[-915,369],[-975,-596],[-395,-134]],[[-135,-601],[575,582],[-667,640]],[[413,890],[-560,-276],[-555,-562]],[[-633,-269],[561,-820],[-624,499]],[[371,-92],[-784,-593],[864,-717]],[[-971,655],[-439,367],[754,-951]],[[172,-347],[36,279],[-247,-402]],[[633,-301],[364,-349],[-683,-387]],[[-780,-211],[-713,-948],[-648,543]],[[72,58],[762,-465],[-66,462]],[[78,502],[781,-832],[713,836]],[[-431,-64],[-484,-392],[208,-343]],[[-64,101],[-29,-860],[-329,844]],[[398,391],[828,-858],[700,395]],[[578,-896],[-326,-604],[314,180]],[[97,-321],[-695,185],[-357,852]],[[854,839],[283,-375],[951,-209]],[[194,96],[-564,-847],[162,524]],[[-354,532],[494,621],[580,560]],[[419,-678],[-450,926],[-5,-924]],[[-661,905],[519,621],[-143,394]],[[-573,268],[296,-562],[-291,-319]],[[-211,266],[-196,158],[564,-183]],[[18,-585],[-398,777],[-581,864]],[[790,-894],[-745,-604],[-418,70]],[[848,-339],[150,773],[11,851]],[[-954,-809],[-53,-20],[-648,-304]],[[658,-336],[-658,-905],[853,407]],[[-365,-844],[350,-625],[852,-358]],[[986,-315],[-230,-159],[21,180]],[[-15,599],[45,-286],[-941,847]],[[-613,-68],[184,639],[-987,550]],[[334,675],[-56,-861],[923,340]],[[-848,-596],[960,231],[-28,-34]],[[707,-811],[-994,-356],[-167,-171]],[[-470,-764],[72,576],[-600,-204]],[[379,189],[-542,-576],[585,800]],[[440,540],[-445,-563],[379,-334]],[[-155,64],[514,-288],[853,106]],[[-304,751],[481,-520],[-708,-694]],[[-709,132],[594,126],[-844,63]],[[723,471],[421,-138],[-962,892]],[[-440,-263],[39,513],[-672,-954]],[[775,809],[-581,330],[752,-107]],[[-376,-158],[335,-708],[-514,578]],[[-343,-769],[456,-187],[25,413]],[[548,-877],[-172,300],[-500,928]],[[938,-102],[423,-488],[-378,-969]],[[-36,564],[-55,131],[958,-800]],[[-322,511],[-413,503],[700,-847]],[[-966,547],[-88,-17],[-359,-67]],[[637,-341],[-437,-181],[527,-153]],[[-74,449],[-28,3],[485,189]],[[-997,658],[-224,-948],[702,-807]],[[-224,736],[-896,127],[-945,-850]],[[-395,-106],[439,-553],[-128,124]],[[-841,-445],[-758,-572],[-489,212]],[[633,-327],[13,-512],[952,771]],[[-940,-171],[-6,-46],[-923,-425]],[[-142,-442],[-817,-998],[843,-695]],[[340,847],[-137,-920],[-988,-658]],[[-653,217],[-679,-257],[651,-719]],[[-294,365],[-41,342],[74,-892]],[[690,-236],[-541,494],[408,-516]],[[180,-807],[225,790],[494,59]],[[707,605],[-246,656],[284,271]],[[65,294],[152,824],[442,-442]],[[-321,781],[-540,341],[316,415]],[[420,371],[-2,545],[995,248]],[[56,-191],[-604,971],[615,449]],[[-981,-31],[510,592],[-390,-362]],[[-317,-968],[913,365],[97,508]],[[832,63],[-864,-510],[86,202]],[[-483,456],[-636,340],[-310,676]],[[981,-847],[751,-508],[-962,-31]],[[-157,99],[73,797],[63,-172]],[[220,858],[872,924],[866,-381]],[[996,-169],[805,321],[-164,971]],[[896,11],[-625,-973],[-782,76]],[[578,-280],[730,-729],[307,-905]],[[-580,-749],[719,-698],[967,603]],[[-821,874],[-103,-623],[662,-491]],[[-763,117],[661,-644],[672,-607]],[[592,787],[-798,-169],[-298,690]],[[296,644],[-526,-762],[-447,665]],[[534,-818],[852,-120],[57,-379]],[[-986,-549],[-329,294],[954,258]],[[-133,352],[-660,-77],[904,-356]],[[748,343],[215,500],[317,-277]],[[311,7],[910,-896],[-809,795]],[[763,-602],[-753,313],[-352,917]],[[668,619],[-474,-597],[-650,650]],[[-297,563],[-701,-987],[486,-902]],[[-461,-740],[-657,233],[-482,-328]],[[-446,-250],[-986,-458],[-629,520]],[[542,-49],[-327,-469],[257,-947]],[[121,-575],[-634,-143],[-184,521]],[[30,504],[455,-645],[-229,-945]],[[-12,-295],[377,764],[771,125]],[[-686,-133],[225,-25],[-376,-143]],[[-6,-46],[338,270],[-405,-872]],[[-623,-37],[582,467],[963,898]],[[-804,869],[-477,420],[-475,-303]],[[94,41],[-842,-193],[-768,720]],[[-656,-918],[415,645],[-357,460]],[[-47,-486],[-911,468],[-608,-686]],[[-158,251],[419,-394],[-655,-895]],[[272,-695],[979,508],[-358,959]],[[-776,650],[-918,-467],[-690,-534]],[[-85,-309],[-626,167],[-366,-429]],[[-880,-732],[-186,-924],[970,-875]],[[517,645],[-274,962],[-804,544]],[[721,402],[104,640],[478,-499]],[[198,684],[-134,-723],[-452,-905]],[[-245,745],[239,238],[-826,441]],[[-217,206],[-32,462],[-981,-895]],[[-51,989],[526,-173],[560,-676]],[[-480,-659],[-976,-580],[-727,466]],[[-996,-90],[-995,158],[-239,642]],[[302,288],[-194,-294],[17,924]],[[-943,969],[-326,114],[-500,103]],[[-619,163],[339,-880],[230,421]],[[-344,-601],[-795,557],[565,-779]],[[590,345],[-129,-202],[-125,-58]],[[-777,-195],[159,674],[775,411]],[[-939,312],[-665,810],[121,855]],[[-971,254],[712,815],[452,581]],[[442,-9],[327,-750],[61,757]],[[-342,869],[869,-160],[390,-772]],[[620,601],[565,-169],[-69,-183]],[[-25,924],[-817,964],[321,-970]],[[-64,-6],[-133,978],[825,-379]],[[601,436],[-24,98],[-115,940]],[[-97,502],[614,-574],[922,513]],[[-125,262],[-946,695],[99,-220]],[[429,-721],[719,-694],[197,-558]],[[326,689],[-70,-908],[-673,338]],[[-468,-856],[-902,-254],[-358,305]],[[-358,530],[542,355],[-253,-47]],[[-438,-74],[-362,963],[988,788]],[[137,717],[467,622],[319,-380]],[[-86,310],[-336,851],[918,-288]],[[721,395],[646,-53],[255,-425]],[[255,175],[912,84],[-209,878]],[[-632,-485],[-400,-357],[991,-608]],[[235,-559],[992,-297],[857,-591]],[[87,-71],[148,130],[647,578]],[[-290,-584],[-639,-788],[-21,592]],[[386,984],[625,-731],[-993,-336]],[[-538,634],[-209,-828],[-150,-774]],[[-754,-387],[607,-781],[976,-199]],[[412,-798],[-664,295],[709,-537]],[[-412,932],[-880,-232],[561,852]],[[-656,-358],[-198,-964],[-433,-848]],[[-762,-668],[-632,186],[-673,-11]],[[-876,237],[-282,-312],[-83,682]],[[403,73],[-57,-436],[-622,781]],[[-587,873],[798,976],[-39,329]],[[-369,-622],[553,-341],[817,794]],[[-108,-616],[920,-849],[-679,96]],[[290,-974],[234,239],[-284,-321]],[[-22,394],[-417,-419],[264,58]],[[-473,-551],[69,923],[591,-228]],[[-956,662],[-113,851],[-581,-794]],[[-258,-681],[413,-471],[-637,-817]],[[-866,926],[992,-653],[-7,794]],[[556,-350],[602,917],[831,-610]],[[188,245],[-906,361],[492,174]],[[-720,384],[-818,329],[638,-666]],[[-246,846],[890,-325],[-59,-850]],[[-118,-509],[620,-762],[-256,15]],[[-787,-536],[-452,-338],[-399,813]],[[458,560],[525,-311],[-608,-419]],[[494,-811],[-825,-127],[-812,894]],[[-801,890],[-629,-860],[574,925]],[[-709,-193],[-213,138],[-410,-403]],[[861,91],[708,-187],[5,-222]],[[789,646],[777,154],[90,-49]],[[-267,-830],[-114,531],[591,-698]],[[-126,-82],[881,-418],[82,652]],[[-894,130],[-726,-935],[393,-815]],[[-142,563],[654,638],[-712,-597]],[[-759,60],[-23,977],[100,-765]],[[-305,595],[-570,-809],[482,762]],[[-161,-267],[53,963],[998,-529]],[[-300,-57],[798,353],[703,486]],[[-990,696],[-764,699],[-565,719]],[[-232,-205],[566,571],[977,369]],[[740,865],[151,-817],[-204,-293]],[[94,445],[-768,229],[537,-406]],[[861,620],[37,-424],[-36,656]],[[390,-369],[952,733],[-464,569]],[[-482,-604],[959,554],[-705,-626]],[[-396,-615],[-991,108],[272,-723]],[[143,780],[535,142],[-917,-147]],[[138,-629],[-217,-908],[905,115]],[[915,103],[-852,64],[-468,-642]],[[570,734],[-785,-268],[-326,-759]],[[738,531],[-332,586],[-779,24]],[[870,440],[-217,473],[-383,415]],[[-296,-333],[-330,-142],[-924,950]],[[118,120],[-35,-245],[-211,-652]],[[61,634],[153,-243],[838,789]],[[726,-582],[210,105],[983,537]],[[-313,-323],[758,234],[29,848]],[[-847,-172],[-593,733],[-56,617]],[[54,255],[-512,156],[-575,675]],[[-873,-956],[-148,623],[95,200]],[[700,-370],[926,649],[-978,157]],[[-639,-202],[719,130],[747,222]],[[194,-33],[955,943],[505,114]],[[-226,-790],[28,-930],[827,783]],[[-392,-74],[-28,714],[218,-612]],[[209,626],[-888,-683],[-912,495]],[[487,751],[614,933],[631,445]],[[-348,-34],[-411,-106],[835,321]],[[-689,872],[-29,-800],[312,-542]],[[-52,566],[827,570],[-862,-77]],[[471,992],[309,-402],[389,912]],[[24,520],[-83,-51],[555,503]],[[-265,-317],[283,-970],[-472,690]],[[606,526],[137,71],[-651,150]],[[217,-518],[663,66],[-605,-331]],[[-562,232],[-76,-503],[205,-323]],[[842,-521],[546,285],[625,-186]],[[997,-927],[344,909],[-546,974]],[[-677,419],[81,121],[-705,771]],[[719,-379],[-944,-797],[784,-155]],[[-378,286],[-317,-797],[-111,964]],[[-288,-573],[784,80],[-532,-646]],[[-77,407],[-248,-797],[769,-816]],[[-24,-637],[287,-858],[-927,-333]],[[-902,37],[894,-823],[141,684]],[[125,467],[-177,-516],[686,399]],[[-321,-542],[641,-590],[527,-224]],[[-400,-712],[-876,-208],[632,-543]],[[-676,-429],[664,-242],[-269,922]],[[-608,-273],[-141,930],[687,380]],[[786,-12],[498,494],[310,326]],[[-739,-617],[606,-960],[804,188]],[[384,-368],[-243,-350],[-459,31]],[[-550,397],[320,-868],[328,-279]],[[969,-179],[853,864],[-110,514]],[[910,793],[302,-822],[-285,488]],[[-605,-128],[218,-283],[-17,-227]],[[16,324],[667,708],[750,3]],[[485,-813],[19,585],[71,930]],[[-218,816],[-687,-97],[-732,-360]],[[-497,-151],[376,-23],[3,315]],[[-412,-989],[-610,-813],[372,964]],[[-878,-280],[87,381],[-311,69]],[[-609,-90],[-731,-679],[150,585]],[[889,27],[-162,605],[75,-770]],[[448,617],[-988,0],[-103,-504]],[[-800,-537],[-69,627],[608,-668]],[[534,686],[-664,942],[830,920]],[[-238,775],[495,932],[-793,497]],[[-343,958],[-914,-514],[-691,651]],[[568,-136],[208,359],[728,28]],[[286,912],[-794,683],[556,-102]],[[-638,-629],[-484,445],[-64,-497]],[[58,505],[-801,-110],[872,632]],[[-390,777],[353,267],[976,369]],[[-993,515],[105,-133],[358,-572]],[[964,996],[355,-212],[-667,38]],[[-725,-614],[-35,365],[132,-196]],[[237,-536],[-416,-302],[312,477]],[[-664,574],[-210,224],[48,-925]],[[869,-261],[-256,-240],[-3,-698]],[[712,385],[32,-34],[916,-315]],[[895,-409],[-100,-346],[728,-624]],[[-806,327],[-450,889],[-781,-939]],[[-586,-403],[698,318],[-939,899]],[[557,-57],[-920,659],[333,-51]],[[-441,232],[-918,-205],[246,1]],[[783,167],[-797,-595],[245,-736]],[[-36,-531],[-486,-426],[-813,-160]],[[777,-843],[817,313],[-228,-572]],[[735,866],[-309,-564],[-81,190]],[[-413,645],[101,719],[-719,218]],[[-83,164],[767,796],[-430,-459]],[[122,779],[-15,-295],[-96,-892]],[[462,379],[70,548],[834,-312]],[[-630,-534],[124,187],[-737,114]],[[-299,-604],[318,-591],[936,826]],[[-879,218],[-642,-483],[-318,-866]],[[-691,62],[-658,761],[-895,-854]],[[-822,493],[687,569],[910,-202]],[[-223,784],[304,-5],[541,925]],[[-914,541],[737,-662],[-662,-195]],[[-622,615],[414,358],[881,-878]],[[339,745],[-268,-968],[-280,-227]],[[-364,855],[148,-709],[-827,472]],[[-890,-532],[-41,664],[-612,577]],[[-702,-859],[971,-722],[-660,-920]],[[-539,-605],[737,149],[973,-802]],[[800,42],[-448,-811],[152,511]],[[-933,377],[-110,-105],[-374,-937]],[[-766,152],[482,120],[-308,390]],[[-568,775],[-292,899],[732,890]],[[-177,-317],[-502,-259],[328,-511]],[[612,-696],[-574,-660],[132,31]],[[-119,563],[-805,-864],[179,-672]],[[425,-627],[183,-331],[839,318]],[[-711,-976],[-749,152],[-916,261]],[[181,-63],[497,211],[262,406]],[[-537,700],[-859,-765],[-928,77]],[[892,832],[231,-749],[-82,613]],[[816,216],[-642,-216],[-669,-912]],[[-6,624],[-937,-370],[-344,268]],[[737,-710],[-869,983],[-324,-274]],[[565,952],[-547,-158],[374,-444]],[[51,-683],[645,-845],[515,636]],[[-953,-631],[114,-377],[-764,-144]],[[-8,470],[-242,-399],[-675,-730]],[[-540,689],[-20,47],[-607,590]],[[-329,-710],[-779,942],[-388,979]],[[123,829],[674,122],[203,563]],[[46,782],[396,-33],[386,610]],[[872,-846],[-523,-122],[-55,-190]],[[388,-994],[-525,974],[127,596]],[[781,-680],[796,-34],[-959,-62]],[[-749,173],[200,-384],[-745,-446]],[[379,618],[136,-250],[-224,970]],[[-58,240],[-921,-760],[-901,-626]],[[366,-185],[565,-100],[515,688]],[[489,999],[-893,-263],[-637,816]],[[838,-496],[-316,-513],[419,479]],[[107,676],[-15,882],[98,-397]],[[-999,941],[-903,-424],[670,-325]],[[171,-979],[835,178],[169,-984]],[[-609,-607],[378,-681],[184,402]],[[-316,903],[-575,-800],[224,983]],[[591,-18],[-460,551],[-167,918]],[[-756,405],[-117,441],[163,-320]],[[456,24],[6,881],[-836,-539]],[[-489,-585],[915,651],[-892,-382]],[[-177,-122],[73,-711],[-386,591]],[[181,724],[530,686],[-131,241]],[[737,288],[886,216],[233,33]],[[-548,-386],[-749,-153],[-85,-982]],[[-835,227],[904,160],[-99,25]],[[-9,-42],[-162,728],[840,-963]],[[217,-763],[870,771],[47,-846]],[[-595,808],[-491,556],[337,-900]],[[-134,281],[-724,441],[-134,708]],[[-789,-508],[651,-962],[661,315]],[[-839,-923],[339,402],[41,-487]],[[300,-790],[48,703],[-398,-811]],[[955,-51],[462,-685],[960,-717]],[[910,-880],[592,-255],[-51,-776]],[[-885,169],[-793,368],[-565,458]],[[-905,940],[-492,-630],[-535,-988]],[[245,797],[763,869],[-82,550]],[[-310,38],[-933,-367],[-650,824]],[[-95,32],[-83,337],[226,990]],[[-218,-975],[-191,-208],[-785,-293]],[[-672,-953],[517,-901],[-247,465]],[[681,-148],[261,-857],[544,-923]],[[640,341],[446,-618],[195,769]],[[384,398],[-846,365],[671,815]],[[578,576],[-911,907],[762,-859]],[[548,-428],[144,-630],[-759,-146]],[[710,-73],[-700,983],[-97,-889]],[[-46,898],[-973,-362],[-817,-717]],[[151,-81],[-125,-900],[-478,-154]],[[483,615],[-537,-932],[181,-68]],[[786,-223],[518,25],[-306,-12]],[[-422,268],[-809,-683],[635,468]],[[983,-734],[-694,-608],[-110,4]],[[-786,-196],[749,-354],[137,-8]],[[-181,36],[668,-200],[691,-973]],[[-629,-838],[692,-736],[437,-871]],[[-208,-536],[-159,-596],[8,197]],[[-3,370],[-686,170],[913,-376]],[[44,-998],[-149,-993],[-200,512]],[[-519,136],[859,497],[536,434]],[[77,-985],[972,-340],[-705,-837]],[[-381,947],[250,360],[344,322]],[[-26,131],[699,750],[707,384]],[[-914,655],[299,193],[406,955]],[[-883,-921],[220,595],[-546,794]],[[-599,577],[-569,-404],[-704,489]],[[-594,-963],[-624,-460],[880,-760]],[[-603,88],[-99,681],[55,-328]],[[976,472],[139,-453],[-531,-860]],[[192,-290],[513,-89],[666,432]],[[417,487],[575,293],[567,-668]],[[655,711],[-162,449],[-980,972]],[[-505,664],[-685,-239],[603,-592]],[[-625,-802],[-67,996],[384,-636]],[[365,-593],[522,-666],[-200,-431]],[[-868,708],[560,-860],[-630,-355]],[[-702,785],[-637,-611],[-597,960]],[[-137,-696],[-93,-803],[408,406]],[[891,-123],[-26,-609],[-610,518]],[[133,-832],[-198,555],[708,-110]],[[791,617],[-69,487],[696,315]],[[-900,694],[-565,517],[-269,-416]],[[914,135],[-781,600],[-71,-600]],[[991,-915],[-422,-351],[-837,313]],[[-840,-398],[-302,21],[590,146]],[[62,-558],[-702,-384],[-625,831]],[[-363,-426],[-924,-496],[792,-908]],[[73,361],[-817,-466],[400,922]],[[-626,-164],[-626,860],[-524,286]],[[255,26],[-944,809],[-606,986]],[[-457,-256],[-103,50],[-867,-871]],[[-223,803],[196,480],[612,136]],[[-820,-928],[700,780],[-977,721]],[[717,332],[53,-933],[-128,793]],[[-602,-648],[562,593],[890,702]],[[-469,-875],[-527,911],[-475,-222]],[[110,-281],[-552,-536],[-816,596]],[[-981,654],[413,-981],[-75,-95]],[[-754,-742],[-515,894],[-220,-344]],[[795,-52],[156,408],[-603,76]],[[474,-157],[423,-499],[-807,-791]],[[260,688],[40,-52],[702,-122]],[[-584,-517],[-390,-881],[302,-504]],[[61,797],[665,708],[14,668]],[[366,166],[458,-614],[564,-983]],[[72,539],[-378,796],[381,-824]],[[-485,201],[-588,842],[736,379]],[[-149,-894],[-298,705],[-303,-406]],[[660,-935],[-580,521],[93,633]],[[-382,-282],[-375,-841],[-828,171]],[[-567,743],[-100,43],[144,122]],[[-281,-786],[-749,-551],[296,304]],[[11,-426],[-792,212],[857,-175]],[[594,143],[-699,289],[315,137]],[[341,596],[-390,107],[-631,-804]],[[-751,-636],[-424,-854],[193,651]],[[-145,384],[749,675],[-786,517]],[[224,-865],[-323,96],[-916,258]],[[-309,403],[-388,826],[35,-270]],[[-942,709],[222,158],[-699,-103]],[[-589,842],[-997,29],[-195,-210]],[[264,426],[566,145],[-217,623]],[[217,965],[507,-601],[-453,507]],[[-206,307],[-982,4],[64,-292]],[[676,-49],[-38,-701],[550,883]],[[5,-850],[-438,659],[745,-773]],[[933,238],[-574,-570],[91,-33]],[[-866,121],[-928,358],[459,-843]],[[-568,-631],[-352,-580],[-349,189]],[[-737,849],[-963,-486],[-662,970]],[[135,334],[-967,-71],[-365,-792]],[[789,21],[-227,51],[990,-275]],[[240,412],[-886,230],[591,256]],[[-609,472],[-853,-754],[959,661]],[[401,521],[521,314],[929,982]],[[-499,784],[-208,71],[-302,296]],[[-557,-948],[-553,-526],[-864,793]],[[270,-626],[828,44],[37,14]],[[-412,224],[617,-593],[502,699]],[[41,-908],[81,562],[-849,163]],[[165,917],[761,-197],[331,-341]],[[-687,314],[799,755],[-969,648]],[[-164,25],[578,439],[-334,-576]],[[213,535],[874,-177],[-551,24]],[[-689,291],[-795,-225],[-496,-125]],[[465,461],[558,-118],[-568,-909]],[[567,660],[-810,46],[-485,878]],[[-147,606],[685,-690],[-774,984]],[[568,-886],[-43,854],[-738,616]],[[-800,386],[-614,585],[764,-226]],[[-518,23],[-225,-732],[-79,440]],[[-173,-291],[-689,636],[642,-447]],[[-598,-16],[227,410],[496,211]],[[-474,-930],[-656,-321],[-420,36]],[[-435,165],[-819,555],[540,144]],[[-969,149],[828,568],[394,648]],[[65,-848],[257,720],[-625,-851]],[[981,899],[275,635],[465,-877]],[[80,290],[792,760],[-191,-321]],[[-605,-858],[594,33],[706,593]],[[585,-472],[318,-35],[354,-927]],[[-365,664],[803,581],[-965,-814]],[[-427,-238],[-480,146],[-55,-606]],[[879,-193],[250,-890],[336,117]],[[-226,-322],[-286,-765],[-836,-218]],[[-913,564],[-667,-698],[937,283]],[[872,-901],[810,-623],[-52,-709]],[[473,171],[717,38],[-429,-644]],[[225,824],[-219,-475],[-180,234]],[[-530,-797],[-948,238],[851,-623]],[[85,975],[-363,529],[598,28]],[[-799,166],[-804,210],[-769,851]],[[-687,-158],[885,736],[-381,-461]],[[447,592],[928,-514],[-515,-661]],[[-399,-777],[-493,80],[-544,-78]],[[-884,631],[171,-825],[-333,551]],[[191,268],[-577,676],[137,-33]],[[212,-853],[709,798],[583,-56]],[[-908,-172],[-540,-84],[-135,-56]],[[303,311],[406,-360],[-240,811]],[[798,-708],[824,59],[234,-57]],[[491,693],[-74,585],[-85,877]],[[509,-65],[-936,329],[-51,722]],[[-122,858],[-52,467],[-77,-609]],[[850,760],[547,-495],[-953,-952]],[[-460,-541],[890,910],[286,724]],[[-914,843],[-579,-983],[-387,-460]],[[989,-171],[-877,-326],[-899,458]],[[846,175],[-915,540],[-1000,-982]],[[-852,-920],[-306,496],[530,-18]],[[338,-991],[160,85],[-455,-661]],[[-186,-311],[-460,-563],[-231,-414]],[[-932,-302],[959,597],[793,748]],[[-366,-402],[-788,-279],[514,53]],[[-940,-956],[447,-956],[211,-285]],[[564,806],[-911,-914],[934,754]],[[575,-858],[-277,15],[409,-714]],[[848,462],[100,-381],[135,242]],[[330,718],[-24,-190],[860,-78]],[[479,458],[941,108],[-866,-653]],[[212,980],[962,-962],[115,841]],[[-827,-474],[-206,881],[323,765]],[[506,-45],[-30,-293],[524,-133]],[[832,-173],[547,-852],[-561,-842]],[[-397,-661],[-708,819],[-545,-228]],[[521,51],[-489,852],[36,-258]],[[227,-164],[189,465],[-987,-882]],[[-73,-997],[641,-995],[449,-615]],[[151,-995],[-638,415],[257,-400]],[[-663,-297],[-748,537],[-734,198]],[[-585,-401],[-81,-782],[-80,-105]],[[99,-21],[238,-365],[-704,-368]],[[45,416],[849,-211],[-371,-1]],[[-404,-443],[795,-406],[36,-933]],[[272,-363],[981,-491],[-380,77]],[[713,-342],[-366,-849],[643,911]],[[-748,671],[-537,813],[961,-200]],[[-194,-909],[703,-662],[-601,188]],[[281,500],[724,286],[267,197]],[[-832,847],[-595,820],[-316,637]],[[520,521],[-54,261],[923,-10]],[[4,-808],[-682,-258],[441,-695]],[[-793,-107],[-969,905],[798,446]],[[-108,-739],[-590,69],[-855,-365]],[[380,-623],[-930,817],[468,713]],[[759,-849],[-236,433],[-723,-931]],[[95,-320],[-686,124],[-69,-329]],[[-655,518],[-210,-523],[284,-866]],[[144,303],[639,70],[-171,269]],[[173,-333],[947,-304],[55,40]],[[274,878],[-482,-888],[-835,375]],[[-982,-854],[-36,-218],[-114,-230]],[[905,-979],[488,-485],[-479,114]],[[877,-157],[553,-530],[-47,-321]],[[350,664],[-881,442],[-220,-284]],[[434,-423],[-365,878],[-726,584]],[[535,909],[-517,-447],[-660,-141]],[[-966,191],[50,353],[182,-642]],[[-785,-634],[123,-907],[-162,511]],[[146,-850],[-214,814],[-704,25]],[[692,1],[521,492],[-637,274]],[[-662,-372],[-313,597],[983,-647]],[[-962,-526],[68,-549],[-819,231]],[[740,-890],[-318,797],[-666,948]],[[-190,-12],[-468,-455],[948,284]],[[16,478],[-506,-888],[628,-154]],[[272,630],[-976,308],[433,3]],[[-169,-391],[-132,189],[302,-388]],[[109,-784],[474,-167],[-265,-31]],[[-177,-532],[283,464],[421,-73]],[[650,635],[592,-138],[1,-387]],[[-932,703],[-827,-492],[-355,686]],[[586,-311],[340,-618],[645,-434]],[[-951,736],[647,-127],[-303,590]],[[188,444],[903,718],[-931,500]],[[-872,-642],[-296,-571],[337,241]],[[23,65],[152,125],[880,470]],[[512,823],[-42,217],[823,-263]],[[180,-831],[-380,886],[607,762]],[[722,443],[-149,-216],[-115,759]],[[-19,660],[-36,901],[923,231]],[[562,-322],[-626,-968],[194,-825]],[[204,-920],[938,784],[362,150]],[[-410,-266],[-715,559],[-672,124]],[[-198,446],[-140,454],[-461,-447]],[[83,-346],[830,-493],[-759,-382]],[[-881,601],[581,234],[-134,-925]],[[-494,914],[-42,899],[235,629]],[[-390,50],[956,437],[774,-700]],[[-514,514],[44,-512],[-576,-313]],[[63,-688],[808,-534],[-570,-399]],[[-726,572],[-896,102],[-294,-28]],[[-688,757],[401,406],[955,-511]],[[-283,423],[-485,480],[-767,908]],[[-541,952],[-594,116],[-854,451]],[[-273,-796],[236,625],[-626,257]],[[-407,-493],[373,826],[-309,297]],[[-750,955],[-476,641],[-809,713]],[[8,415],[695,226],[-111,2]],[[733,209],[152,-920],[401,995]],[[921,-103],[-919,66],[871,-947]],[[-907,89],[-869,-214],[851,-559]],[[-307,748],[524,-755],[314,-711]],[[188,897],[-72,-763],[482,103]],[[545,-821],[-232,-596],[-334,-754]],[[-217,-788],[-820,388],[-200,-662]],[[779,160],[-723,-975],[-142,-998]],[[-978,-519],[-78,-981],[842,904]],[[-504,-736],[-295,21],[-472,-482]],[[391,115],[-705,574],[652,-446]],[[813,-988],[865,830],[-263,487]],[[194,80],[774,-493],[-761,-872]],[[-415,-284],[-803,7],[-810,670]],[[-484,-4],[881,-872],[55,-852]],[[-379,822],[-266,324],[-48,748]],[[-304,-278],[406,-60],[959,-89]],[[404,756],[577,-643],[-332,658]],[[291,460],[125,491],[-312,83]],[[311,-734],[-141,582],[282,-557]],[[-450,-661],[-981,710],[-177,794]],[[328,264],[-787,971],[-743,-407]],[[-622,518],[993,-241],[-738,229]],[[273,-826],[-254,-917],[-710,-111]],[[809,770],[96,368],[-818,725]],[[-488,773],[502,-342],[534,745]],[[-28,-414],[236,-315],[-484,363]],[[179,-466],[-566,713],[-683,56]],[[560,-240],[-597,619],[916,-940]],[[893,473],[872,-868],[-642,-461]],[[799,489],[383,-321],[-776,-833]],[[980,490],[-508,764],[-512,-426]],[[917,961],[-16,-675],[440,559]],[[-812,212],[784,-987],[-132,554]],[[-886,454],[747,806],[190,231]],[[910,341],[21,-66],[708,725]],[[29,929],[-831,-494],[-303,389]],[[-103,492],[-271,-174],[-515,529]],[[-292,119],[419,788],[247,-951]],[[483,543],[-347,-673],[664,-549]],[[-926,-871],[-437,337],[162,-877]],[[299,472],[-771,5],[-88,-643]],[[-103,525],[-725,-998],[264,22]],[[-505,708],[550,-545],[823,347]],[[-738,931],[59,147],[-156,-259]],[[456,968],[-162,889],[132,-911]],[[535,120],[968,-517],[-864,-541]],[[24,-395],[-593,-766],[-565,-332]],[[834,611],[825,-576],[280,629]],[[211,-548],[140,-278],[-592,929]],[[-999,-240],[-63,-78],[793,573]],[[-573,160],[450,987],[529,322]],[[63,353],[315,-187],[-461,577]],[[189,-950],[-247,656],[289,241]],[[209,-297],[397,664],[-805,484]],[[-655,452],[435,-556],[917,874]],[[253,-756],[262,-888],[-778,-214]],[[793,-451],[323,-251],[-401,-458]],[[-396,619],[-651,-287],[-668,-781]],[[698,720],[-349,742],[-807,546]],[[738,280],[680,279],[-540,858]],[[-789,387],[530,-36],[-551,-491]],[[162,579],[-427,-272],[228,710]],[[689,356],[917,-580],[729,217]],[[-115,-638],[866,424],[-82,-194]],[[411,-338],[-917,172],[227,-29]],[[-612,63],[630,-976],[-64,-204]],[[-200,911],[583,-571],[682,-579]],[[91,298],[396,-183],[788,-955]],[[141,-873],[-277,149],[-396,916]],[[321,958],[-136,573],[541,-777]],[[797,-909],[-469,-877],[988,-653]],[[784,-198],[129,883],[-203,399]],[[-68,-810],[223,-423],[-467,-512]],[[531,-445],[-603,-997],[-841,641]],[[-274,-242],[174,261],[-636,-158]],[[-574,494],[-796,-798],[-798,99]],[[95,-82],[-613,-954],[-753,986]],[[-883,-448],[-864,-401],[938,-392]],[[913,930],[-542,-988],[310,410]],[[506,-99],[43,512],[790,-222]],[[724,31],[49,-950],[260,-134]],[[-287,-947],[-234,-700],[56,588]],[[-33,782],[-144,948],[105,-791]],[[548,-546],[-652,-293],[881,-520]],[[691,-91],[76,991],[-631,742]],[[-520,-429],[-244,-296],[724,-48]],[[778,646],[377,50],[-188,56]],[[-895,-507],[-898,-165],[-674,652]],[[654,584],[-634,177],[-349,-620]],[[114,-980],[355,62],[182,975]],[[516,9],[-442,-298],[274,-579]],[[-238,262],[-431,-896],[506,-850]],[[47,748],[846,821],[-537,-293]],[[839,726],[593,285],[-297,840]],[[634,-486],[468,-304],[-887,-567]],[[-864,914],[296,-124],[335,233]],[[88,-253],[-523,-956],[-554,803]],[[-587,417],[281,-62],[-409,-363]],[[-136,-39],[-292,-768],[-264,876]],[[-127,506],[-891,-331],[-744,-430]],[[778,584],[-750,-129],[-479,-94]],[[-876,-771],[-987,-757],[180,-641]],[[-777,-694],[411,-87],[329,190]],[[-347,-999],[-882,158],[-754,232]],[[-105,918],[188,237],[-110,-591]],[[-209,703],[-838,77],[838,909]],[[-995,-339],[-762,750],[860,472]],[[185,271],[-289,173],[811,-300]],[[2,65],[-656,-22],[36,-139]],[[765,-210],[883,974],[961,-905]],[[-212,295],[-615,-840],[77,474]],[[211,-910],[-440,703],[-11,859]],[[-559,-4],[-196,841],[-277,969]],[[-73,-159],[-887,126],[978,-371]],[[-569,633],[-423,-33],[512,-393]],[[503,143],[-383,-109],[-649,-998]],[[-663,339],[-317,-523],[-2,596]],[[690,-380],[570,378],[-652,132]],[[72,-744],[-930,399],[-525,935]],[[865,-983],[115,37],[995,826]],[[594,-621],[-872,443],[188,-241]],[[-1000,291],[754,234],[-435,-869]],[[-868,901],[654,-907],[59,181]],[[-868,-793],[-431,596],[-446,-564]],[[900,-944],[-680,-796],[902,-366]],[[331,430],[943,853],[-851,-942]],[[315,-538],[-354,-909],[139,721]],[[170,-884],[-225,-818],[-808,-657]],[[-279,-34],[-533,-871],[-972,552]],[[691,-986],[-800,-950],[654,-747]],[[603,988],[899,841],[-630,591]],[[876,-949],[809,562],[602,-536]],[[-693,363],[-189,495],[738,-1000]],[[-383,431],[-633,297],[665,959]],[[-740,686],[-207,-803],[188,-520]],[[-820,226],[31,-339],[10,121]],[[-312,-844],[624,-516],[483,621]],[[-822,-529],[69,-278],[800,328]],[[834,-82],[-759,420],[811,-264]],[[-960,-240],[-921,561],[173,46]],[[-324,909],[-790,-814],[-2,-785]],[[976,334],[-290,-891],[704,-581]],[[150,-798],[689,-823],[237,-639]],[[-551,-320],[876,-502],[-622,-628]],[[-136,845],[904,595],[-702,-261]],[[-857,-377],[-522,-101],[-943,-805]],[[-682,-787],[-888,-459],[-752,-985]],[[-571,-81],[623,-133],[447,643]],[[-375,-158],[72,-387],[-324,-696]],[[-660,-650],[340,188],[569,526]],[[727,-218],[16,-7],[-595,-988]],[[-966,-684],[802,-783],[-272,-194]],[[115,-566],[-888,47],[712,180]],[[-237,-69],[45,-272],[981,-812]],[[48,897],[439,417],[50,325]],[[348,616],[180,254],[104,-784]],[[-730,811],[-548,612],[-736,790]],[[138,-810],[123,930],[65,865]],[[-768,-299],[-49,-895],[-692,-418]],[[487,-531],[802,-159],[-12,634]],[[808,-179],[552,-73],[470,717]],[[720,-644],[886,-141],[625,144]],[[-485,-505],[-347,-244],[-916,66]],[[600,-565],[995,-5],[324,227]],[[-771,-35],[904,-482],[753,-303]],[[-701,65],[426,-763],[-504,-479]],[[409,733],[-823,475],[64,718]],[[865,975],[368,893],[-413,-433]],[[812,-597],[-970,819],[813,624]],[[193,-642],[-381,-560],[545,398]],[[711,28],[-316,771],[717,-865]],[[-509,462],[809,-136],[786,635]],[[618,-49],[484,169],[635,547]],[[-747,685],[-882,-496],[-332,82]],[[-501,-851],[870,563],[290,570]],[[-279,-829],[-509,397],[457,816]],[[-508,80],[850,-188],[483,-326]],[[860,-100],[360,119],[-205,787]],[[-870,21],[-39,-827],[-185,932]],[[826,284],[-136,-866],[-330,-97]],[[-944,-82],[745,899],[-97,365]],[[929,262],[564,632],[-115,632]],[[244,-276],[713,330],[-897,-214]],[[-890,-109],[664,876],[-974,-907]],[[716,249],[816,489],[723,141]],[[-96,-560],[-272,45],[-70,645]],[[762,-503],[414,-828],[-254,-646]],[[909,-13],[903,-422],[-344,-10]],[[658,-486],[743,545],[50,674]],[[-241,507],[-367,18],[-48,-241]],[[886,-268],[884,-762],[120,-486]],[[-412,-528],[879,-647],[223,-393]],[[851,810],[234,937],[-726,797]],[[-999,942],[839,-134],[-996,-189]],[[100,979],[-527,-521],[378,800]],[[544,-844],[-832,-530],[-77,-641]],[[43,889],[31,442],[-934,-503]],[[-330,-370],[-309,-439],[173,547]],[[169,945],[62,-753],[-542,-597]],[[208,751],[-372,-647],[-520,70]],[[765,-840],[907,-257],[379,918]],[[334,-135],[-689,730],[-427,618]],[[137,-508],[66,-695],[78,169]],[[-962,-123],[400,-417],[151,969]],[[328,689],[666,427],[-555,-642]],[[-907,343],[605,-341],[-647,582]],[[-667,-363],[-571,818],[-265,-399]],[[525,-938],[904,898],[725,692]],[[-176,-802],[-858,-9],[780,275]],[[580,170],[-740,287],[691,-97]],[[365,557],[-375,361],[-288,859]],[[193,737],[842,-808],[520,282]],[[-871,65],[-799,836],[179,-720]],[[958,-144],[744,-789],[797,-48]],[[122,582],[662,912],[68,757]],[[595,241],[-801,513],[388,186]],[[-103,-677],[-259,-731],[-281,-857]],[[921,319],[-696,683],[-88,-997]],[[775,200],[78,858],[648,768]],[[316,821],[-763,68],[-290,-741]],[[564,664],[691,504],[760,787]],[[694,-119],[973,-385],[309,-760]],[[777,-947],[-57,990],[74,19]],[[971,626],[-496,-781],[-602,-239]],[[-651,433],[11,-339],[939,294]],[[-965,-728],[560,569],[-708,-247]]
+];
+```
+
+## --seed-contents--
+
+```js
+function triangleContainment(triangles) {
+
+ return true;
+}
+
+const testTriangles1 = [
+ [[-866,121],[-928,358],[459,-843]],[[-568,-631],[-352,-580],[-349,189]],[[-737,849],[-963,-486],[-662,970]],[[135,334],[-967,-71],[-365,-792]],[[789,21],[-227,51],[990,-275]],[[240,412],[-886,230],[591,256]],[[-609,472],[-853,-754],[959,661]],[[401,521],[521,314],[929,982]],[[-499,784],[-208,71],[-302,296]],[[-557,-948],[-553,-526],[-864,793]],[[270,-626],[828,44],[37,14]],[[-412,224],[617,-593],[502,699]],[[41,-908],[81,562],[-849,163]],[[165,917],[761,-197],[331,-341]],[[-687,314],[799,755],[-969,648]],[[-164,25],[578,439],[-334,-576]],[[213,535],[874,-177],[-551,24]],[[-689,291],[-795,-225],[-496,-125]],[[465,461],[558,-118],[-568,-909]],[[567,660],[-810,46],[-485,878]],[[-147,606],[685,-690],[-774,984]],[[568,-886],[-43,854],[-738,616]],[[-800,386],[-614,585],[764,-226]],[[-518,23],[-225,-732],[-79,440]],[[-173,-291],[-689,636],[642,-447]],[[-598,-16],[227,410],[496,211]],[[-474,-930],[-656,-321],[-420,36]],[[-435,165],[-819,555],[540,144]],[[-969,149],[828,568],[394,648]],[[65,-848],[257,720],[-625,-851]],[[981,899],[275,635],[465,-877]],[[80,290],[792,760],[-191,-321]],[[-605,-858],[594,33],[706,593]],[[585,-472],[318,-35],[354,-927]],[[-365,664],[803,581],[-965,-814]],[[-427,-238],[-480,146],[-55,-606]],[[879,-193],[250,-890],[336,117]],[[-226,-322],[-286,-765],[-836,-218]],[[-913,564],[-667,-698],[937,283]],[[872,-901],[810,-623],[-52,-709]],[[473,171],[717,38],[-429,-644]],[[225,824],[-219,-475],[-180,234]],[[-530,-797],[-948,238],[851,-623]],[[85,975],[-363,529],[598,28]],[[-799,166],[-804,210],[-769,851]],[[-687,-158],[885,736],[-381,-461]],[[447,592],[928,-514],[-515,-661]],[[-399,-777],[-493,80],[-544,-78]],[[-884,631],[171,-825],[-333,551]],[[191,268],[-577,676],[137,-33]],[[212,-853],[709,798],[583,-56]],[[-908,-172],[-540,-84],[-135,-56]],[[303,311],[406,-360],[-240,811]],[[798,-708],[824,59],[234,-57]],[[491,693],[-74,585],[-85,877]],[[509,-65],[-936,329],[-51,722]],[[-122,858],[-52,467],[-77,-609]],[[850,760],[547,-495],[-953,-952]],[[-460,-541],[890,910],[286,724]],[[-914,843],[-579,-983],[-387,-460]],[[989,-171],[-877,-326],[-899,458]],[[846,175],[-915,540],[-1000,-982]],[[-852,-920],[-306,496],[530,-18]],[[338,-991],[160,85],[-455,-661]],[[-186,-311],[-460,-563],[-231,-414]],[[-932,-302],[959,597],[793,748]],[[-366,-402],[-788,-279],[514,53]],[[-940,-956],[447,-956],[211,-285]],[[564,806],[-911,-914],[934,754]],[[575,-858],[-277,15],[409,-714]]
+];
+
+triangleContainment(testTriangles1);
+```
+
+# --solutions--
+
+```js
+function triangleContainment(triangles) {
+ function isInTriangle(triangle, point) {
+ // Based on https://stackoverflow.com/a/14382692
+ const area = triangleArea(triangle);
+ const s = getS(area, point, triangle);
+ const t = getT(area, point, triangle);
+
+ if (s > 0 && t > 0 && 1 - s - t > 0) {
+ return true;
+ }
+ return false;
+ }
+
+ function getS(area, point, triangle) {
+ return (
+ (1 / (2 * area)) *
+ (triangle.A.y * triangle.C.x -
+ triangle.A.x * triangle.C.y +
+ point.x * (triangle.C.y - triangle.A.y) +
+ point.y * (triangle.A.x - triangle.C.x))
+ );
+ }
+
+ function getT(area, point, triangle) {
+ return (
+ (1 / (2 * area)) *
+ (triangle.A.x * triangle.B.y -
+ triangle.A.y * triangle.B.x +
+ point.x * (triangle.A.y - triangle.B.y) +
+ point.y * (triangle.B.x - triangle.A.x))
+ );
+ }
+
+ function triangleArea(triangle) {
+ return (
+ 0.5 *
+ (-triangle.B.y * triangle.C.x +
+ triangle.A.y * (-triangle.B.x + triangle.C.x) +
+ triangle.A.x * (triangle.B.y - triangle.C.y) +
+ triangle.B.x * triangle.C.y)
+ );
+ }
+
+ function parseTriangle(triangle) {
+ const points = [];
+ for (let i = 0; i < triangle.length; i++) {
+ const [coordinateX, coordinateY] = triangle[i];
+ points.push({ x: coordinateX, y: coordinateY });
+ }
+ const [pointA, pointB, pointC] = points;
+ return {
+ A: pointA,
+ B: pointB,
+ C: pointC
+ };
+ }
+
+ const origin = { x: 0, y: 0 };
+
+ let trianglesInside = 0;
+ for (let i = 0; i < triangles.length; i++) {
+ const triangle = parseTriangle(triangles[i]);
+
+ if (isInTriangle(triangle, origin)) {
+ trianglesInside++;
+ }
+ }
+ return trianglesInside;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-103-special-subset-sums-optimum.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-103-special-subset-sums-optimum.md
new file mode 100644
index 00000000000..bf85eef1f76
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-103-special-subset-sums-optimum.md
@@ -0,0 +1,56 @@
+---
+id: 5900f3d61000cf542c50fee7
+title: 'Problem 103: Special subset sums: optimum'
+challengeType: 1
+forumTopicId: 301727
+dashedName: problem-103-special-subset-sums-optimum
+---
+
+# --description--
+
+Let $S(A)$ represent the sum of elements in set A of size n. We shall call it a special sum set if for any two non-empty disjoint subsets, B and C, the following properties are true:
+
+1. $S(B) ≠ S(C)$; that is, sums of subsets cannot be equal.
+2. If B contains more elements than C then $S(B) > S(C)$.
+
+If $S(A)$ is minimised for a given n, we shall call it an optimum special sum set. The first five optimum special sum sets are given below.
+
+$$\begin{align} & n = 1: \\{1\\} \\\\
+ & n = 2: \\{1, 2\\} \\\\ & n = 3: \\{2, 3, 4\\} \\\\
+ & n = 4: \\{3, 5, 6, 7\\} \\\\ & n = 5: \\{6, 9, 11, 12, 13\\} \\\\
+\end{align}$$
+
+It seems that for a given optimum set, $A = \\{a_1, a_2, \ldots, a_n\\}$, the next optimum set is of the form $B = \\{b, a_1 + b, a_2 + b, \ldots, a_n + b\\}$, where b is the "middle" element on the previous row.
+
+By applying this "rule" we would expect the optimum set for $n = 6$ to be $A = \\{11, 17, 20, 22, 23, 24\\}$, with $S(A) = 117$. However, this is not the optimum set, as we have merely applied an algorithm to provide a near optimum set. The optimum set for $n = 6$ is $A = \\{11, 18, 19, 20, 22, 25\\}$, with $S(A) = 115$ and corresponding set string: `111819202225`.
+
+Given that A is an optimum special sum set for $n = 7$, find its set string.
+
+**Note:** This problem is related to Problem 105 and Problem 106.
+
+# --hints--
+
+`optimumSpecialSumSet()` should return the string `20313839404245`.
+
+```js
+assert.strictEqual(optimumSpecialSumSet(), '20313839404245');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function optimumSpecialSumSet() {
+
+ return true;
+}
+
+optimumSpecialSumSet();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-104-pandigital-fibonacci-ends.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-104-pandigital-fibonacci-ends.md
new file mode 100644
index 00000000000..baa7dcbfdbd
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-104-pandigital-fibonacci-ends.md
@@ -0,0 +1,44 @@
+---
+id: 5900f3d51000cf542c50fee6
+title: 'Problem 104: Pandigital Fibonacci ends'
+challengeType: 1
+forumTopicId: 301728
+dashedName: problem-104-pandigital-fibonacci-ends
+---
+
+# --description--
+
+The Fibonacci sequence is defined by the recurrence relation:
+
+$F_n = F_{n − 1} + F_{n − 2}$, where $F_1 = 1$ and $F_2 = 1$
+
+It turns out that $F_{541}$, which contains 113 digits, is the first Fibonacci number for which the last nine digits are 1 - 9 pandigital (contain all the digits 1 to 9, but not necessarily in order). And $F_{2749}$, which contains 575 digits, is the first Fibonacci number for which the first nine digits are 1 - 9 pandigital.
+
+Given that $F_k$ is the first Fibonacci number for which the first nine digits AND the last nine digits are 1 - 9 pandigital, find `k`.
+
+# --hints--
+
+`pandigitalFibonacciEnds()` should return `329468`.
+
+```js
+assert.strictEqual(pandigitalFibonacciEnds(), 329468);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pandigitalFibonacciEnds() {
+
+ return true;
+}
+
+pandigitalFibonacciEnds();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-105-special-subset-sums-testing.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-105-special-subset-sums-testing.md
new file mode 100644
index 00000000000..1636463728d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-105-special-subset-sums-testing.md
@@ -0,0 +1,59 @@
+---
+id: 5900f3d61000cf542c50fee8
+title: 'Problem 105: Special subset sums: testing'
+challengeType: 1
+forumTopicId: 301729
+dashedName: problem-105-special-subset-sums-testing
+---
+
+# --description--
+
+Let $S(A)$ represent the sum of elements in set A of size n. We shall call it a special sum set if for any two non-empty disjoint subsets, B and C, the following properties are true:
+
+1. $S(B) ≠ S(C)$; that is, sums of subsets cannot be equal.
+2. If B contains more elements than C then $S(B) > S(C)$.
+
+For example, {81, 88, 75, 42, 87, 84, 86, 65} is not a special sum set because 65 + 87 + 88 = 75 + 81 + 84, whereas {157, 150, 164, 119, 79, 159, 161, 139, 158} satisfies both rules for all possible subset pair combinations and $S(A) = 1286$.
+
+Using `sets`, an array with one-hundred sets, containing seven to twelve elements (the two examples given above are the first two sets), identify all the special sum sets, $A_1, A_2, \ldots, A_k$, and find the value of $(A_1) + S(A_2) + \cdots + S(A_k)$.
+
+**Note:** This problem is related to Problem 103 and Problem 106.
+
+# --hints--
+
+`testingSpecialSubsetSums(testSets)` should return `73702`.
+
+```js
+assert.strictEqual(testingSpecialSubsetSums(_testSets), 73702);
+```
+
+# --seed--
+
+## --after-user-code--
+
+```js
+const _testSets = [
+ [81,88,75,42,87,84,86,65],[157,150,164,119,79,159,161,139,158],[673,465,569,603,629,592,584,300,601,599,600],[90,85,83,84,65,87,76,46],[165,168,169,190,162,85,176,167,127],[224,275,278,249,277,279,289,295,139],[354,370,362,384,359,324,360,180,350,270],[599,595,557,298,448,596,577,667,597,588,602],[175,199,137,88,187,173,168,171,174],[93,187,196,144,185,178,186,202,182],[157,155,81,158,119,176,152,167,159],[184,165,159,166,163,167,174,124,83],[1211,1212,1287,605,1208,1189,1060,1216,1243,1200,908,1210],[339,299,153,305,282,304,313,306,302,228],[94,104,63,112,80,84,93,96],[41,88,82,85,61,74,83,81],[90,67,84,83,82,97,86,41],[299,303,151,301,291,302,307,377,333,280],[55,40,48,44,25,42,41],[1038,1188,1255,1184,594,890,1173,1151,1186,1203,1187,1195],[76,132,133,144,135,99,128,154],[77,46,108,81,85,84,93,83],[624,596,391,605,529,610,607,568,604,603,453],[83,167,166,189,163,174,160,165,133],[308,281,389,292,346,303,302,304,300,173],[593,1151,1187,1184,890,1040,1173,1186,1195,1255,1188,1203],[68,46,64,33,60,58,65],[65,43,88,87,86,99,93,90],[83,78,107,48,84,87,96,85],[1188,1173,1256,1038,1187,1151,890,1186,1184,1203,594,1195],[302,324,280,296,294,160,367,298,264,299],[521,760,682,687,646,664,342,698,692,686,672],[56,95,86,97,96,89,108,120],[344,356,262,343,340,382,337,175,361,330],[47,44,42,27,41,40,37],[139,155,161,158,118,166,154,156,78],[118,157,164,158,161,79,139,150,159],[299,292,371,150,300,301,281,303,306,262],[85,77,86,84,44,88,91,67],[88,85,84,44,65,91,76,86],[138,141,127,96,136,154,135,76],[292,308,302,346,300,324,304,305,238,166],[354,342,341,257,348,343,345,321,170,301],[84,178,168,167,131,170,193,166,162],[686,701,706,673,694,687,652,343,683,606,518],[295,293,301,367,296,279,297,263,323,159],[1038,1184,593,890,1188,1173,1187,1186,1195,1150,1203,1255],[343,364,388,402,191,383,382,385,288,374],[1187,1036,1183,591,1184,1175,888,1197,1182,1219,1115,1167],[151,291,307,303,345,238,299,323,301,302],[140,151,143,138,99,69,131,137],[29,44,42,59,41,36,40],[348,329,343,344,338,315,169,359,375,271],[48,39,34,37,50,40,41],[593,445,595,558,662,602,591,297,610,580,594],[686,651,681,342,541,687,691,707,604,675,699],[180,99,189,166,194,188,144,187,199],[321,349,335,343,377,176,265,356,344,332],[1151,1255,1195,1173,1184,1186,1188,1187,1203,593,1038,891],[90,88,100,83,62,113,80,89],[308,303,238,300,151,304,324,293,346,302],[59,38,50,41,42,35,40],[352,366,174,355,344,265,343,310,338,331],[91,89,93,90,117,85,60,106],[146,186,166,175,202,92,184,183,189],[82,67,96,44,80,79,88,76],[54,50,58,66,31,61,64],[343,266,344,172,308,336,364,350,359,333],[88,49,87,82,90,98,86,115],[20,47,49,51,54,48,40],[159,79,177,158,157,152,155,167,118],[1219,1183,1182,1115,1035,1186,591,1197,1167,887,1184,1175],[611,518,693,343,704,667,686,682,677,687,725],[607,599,634,305,677,604,603,580,452,605,591],[682,686,635,675,692,730,687,342,517,658,695],[662,296,573,598,592,584,553,593,595,443,591],[180,185,186,199,187,210,93,177,149],[197,136,179,185,156,182,180,178,99],[271,298,218,279,285,282,280,238,140],[1187,1151,890,593,1194,1188,1184,1173,1038,1186,1255,1203],[169,161,177,192,130,165,84,167,168],[50,42,43,41,66,39,36],[590,669,604,579,448,599,560,299,601,597,598],[174,191,206,179,184,142,177,180,90],[298,299,297,306,164,285,374,269,329,295],[181,172,162,138,170,195,86,169,168],[1184,1197,591,1182,1186,889,1167,1219,1183,1033,1115,1175],[644,695,691,679,667,687,340,681,770,686,517],[606,524,592,576,628,593,591,584,296,444,595],[94,127,154,138,135,74,136,141],[179,168,172,178,177,89,198,186,137],[302,299,291,300,298,149,260,305,280,370],[678,517,670,686,682,768,687,648,342,692,702],[302,290,304,376,333,303,306,298,279,153],[95,102,109,54,96,75,85,97],[150,154,146,78,152,151,162,173,119],[150,143,157,152,184,112,154,151,132],[36,41,54,40,25,44,42],[37,48,34,59,39,41,40],[681,603,638,611,584,303,454,607,606,605,596]
+];
+```
+
+## --seed-contents--
+
+```js
+function testingSpecialSubsetSums(sets) {
+
+ return true;
+}
+
+const testSets = [
+ [81,88,75,42,87,84,86,65],[157,150,164,119,79,159,161,139,158],[673,465,569,603,629,592,584,300,601,599,600],[90,85,83,84,65,87,76,46],[165,168,169,190,162,85,176,167,127],[224,275,278,249,277,279,289,295,139],[354,370,362,384,359,324,360,180,350,270],[599,595,557,298,448,596,577,667,597,588,602],[175,199,137,88,187,173,168,171,174],[93,187,196,144,185,178,186,202,182],[157,155,81,158,119,176,152,167,159],[184,165,159,166,163,167,174,124,83],[1211,1212,1287,605,1208,1189,1060,1216,1243,1200,908,1210],[339,299,153,305,282,304,313,306,302,228],[94,104,63,112,80,84,93,96],[41,88,82,85,61,74,83,81],[90,67,84,83,82,97,86,41],[299,303,151,301,291,302,307,377,333,280],[55,40,48,44,25,42,41],[1038,1188,1255,1184,594,890,1173,1151,1186,1203,1187,1195],[76,132,133,144,135,99,128,154],[77,46,108,81,85,84,93,83],[624,596,391,605,529,610,607,568,604,603,453],[83,167,166,189,163,174,160,165,133],[308,281,389,292,346,303,302,304,300,173],[593,1151,1187,1184,890,1040,1173,1186,1195,1255,1188,1203],[68,46,64,33,60,58,65],[65,43,88,87,86,99,93,90],[83,78,107,48,84,87,96,85],[1188,1173,1256,1038,1187,1151,890,1186,1184,1203,594,1195],[302,324,280,296,294,160,367,298,264,299],[521,760,682,687,646,664,342,698,692,686,672],[56,95,86,97,96,89,108,120],[344,356,262,343,340,382,337,175,361,330],[47,44,42,27,41,40,37],[139,155,161,158,118,166,154,156,78],[118,157,164,158,161,79,139,150,159],[299,292,371,150,300,301,281,303,306,262],[85,77,86,84,44,88,91,67],[88,85,84,44,65,91,76,86],[138,141,127,96,136,154,135,76],[292,308,302,346,300,324,304,305,238,166],[354,342,341,257,348,343,345,321,170,301],[84,178,168,167,131,170,193,166,162],[686,701,706,673,694,687,652,343,683,606,518],[295,293,301,367,296,279,297,263,323,159],[1038,1184,593,890,1188,1173,1187,1186,1195,1150,1203,1255],[343,364,388,402,191,383,382,385,288,374],[1187,1036,1183,591,1184,1175,888,1197,1182,1219,1115,1167],[151,291,307,303,345,238,299,323,301,302],[140,151,143,138,99,69,131,137],[29,44,42,59,41,36,40],[348,329,343,344,338,315,169,359,375,271],[48,39,34,37,50,40,41],[593,445,595,558,662,602,591,297,610,580,594],[686,651,681,342,541,687,691,707,604,675,699],[180,99,189,166,194,188,144,187,199],[321,349,335,343,377,176,265,356,344,332],[1151,1255,1195,1173,1184,1186,1188,1187,1203,593,1038,891],[90,88,100,83,62,113,80,89],[308,303,238,300,151,304,324,293,346,302],[59,38,50,41,42,35,40],[352,366,174,355,344,265,343,310,338,331],[91,89,93,90,117,85,60,106],[146,186,166,175,202,92,184,183,189],[82,67,96,44,80,79,88,76],[54,50,58,66,31,61,64],[343,266,344,172,308,336,364,350,359,333],[88,49,87,82,90,98,86,115],[20,47,49,51,54,48,40],[159,79,177,158,157,152,155,167,118],[1219,1183,1182,1115,1035,1186,591,1197,1167,887,1184,1175],[611,518,693,343,704,667,686,682,677,687,725],[607,599,634,305,677,604,603,580,452,605,591],[682,686,635,675,692,730,687,342,517,658,695],[662,296,573,598,592,584,553,593,595,443,591],[180,185,186,199,187,210,93,177,149],[197,136,179,185,156,182,180,178,99],[271,298,218,279,285,282,280,238,140],[1187,1151,890,593,1194,1188,1184,1173,1038,1186,1255,1203],[169,161,177,192,130,165,84,167,168],[50,42,43,41,66,39,36],[590,669,604,579,448,599,560,299,601,597,598],[174,191,206,179,184,142,177,180,90],[298,299,297,306,164,285,374,269,329,295],[181,172,162,138,170,195,86,169,168],[1184,1197,591,1182,1186,889,1167,1219,1183,1033,1115,1175],[644,695,691,679,667,687,340,681,770,686,517],[606,524,592,576,628,593,591,584,296,444,595],[94,127,154,138,135,74,136,141],[179,168,172,178,177,89,198,186,137],[302,299,291,300,298,149,260,305,280,370],[678,517,670,686,682,768,687,648,342,692,702],[302,290,304,376,333,303,306,298,279,153],[95,102,109,54,96,75,85,97],[150,154,146,78,152,151,162,173,119],[150,143,157,152,184,112,154,151,132],[36,41,54,40,25,44,42],[37,48,34,59,39,41,40],[681,603,638,611,584,303,454,607,606,605,596]
+];
+
+testingSpecialSubsetSums(testSets);
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-106-special-subset-sums-meta-testing.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-106-special-subset-sums-meta-testing.md
new file mode 100644
index 00000000000..67638b56e90
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-106-special-subset-sums-meta-testing.md
@@ -0,0 +1,49 @@
+---
+id: 5900f3d71000cf542c50fee9
+title: 'Problem 106: Special subset sums: meta-testing'
+challengeType: 1
+forumTopicId: 301730
+dashedName: problem-106-special-subset-sums-meta-testing
+---
+
+# --description--
+
+Let $S(A)$ represent the sum of elements in set A of size n. We shall call it a special sum set if for any two non-empty disjoint subsets, B and C, the following properties are true:
+
+1. $S(B) ≠ S(C)$; that is, sums of subsets cannot be equal.
+2. If B contains more elements than C then $S(B) > S(C)$.
+
+For this problem we shall assume that a given set contains n strictly increasing elements and it already satisfies the second rule.
+
+Surprisingly, out of the 25 possible subset pairs that can be obtained from a set for which n = 4, only 1 of these pairs need to be tested for equality (first rule). Similarly, when n = 7, only 70 out of the 966 subset pairs need to be tested.
+
+For n = 12, how many of the 261625 subset pairs that can be obtained need to be tested for equality?
+
+**Note:** This problem is related to Problem 103 and Problem 105.
+
+# --hints--
+
+`subsetSumsMetaTesting()` should return `21384`.
+
+```js
+assert.strictEqual(subsetSumsMetaTesting(), 21384);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function subsetSumsMetaTesting() {
+
+ return true;
+}
+
+subsetSumsMetaTesting();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-107-minimal-network.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-107-minimal-network.md
new file mode 100644
index 00000000000..3b69363096d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-107-minimal-network.md
@@ -0,0 +1,71 @@
+---
+id: 5900f3d91000cf542c50feea
+title: 'Problem 107: Minimal network'
+challengeType: 1
+forumTopicId: 301731
+dashedName: problem-107-minimal-network
+---
+
+# --description--
+
+The following undirected network consists of seven vertices and twelve edges with a total weight of 243.
+
+
+
|
+
+  + |
+
+
|
+
+
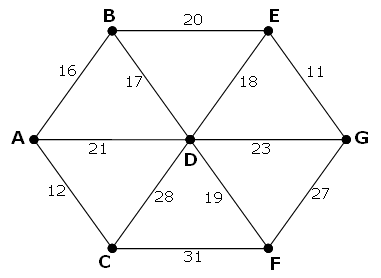+The same network can be represented by the matrix below.
+
+| | A | B | C | D | E | F | G |
+| - | -- | -- | -- | -- | -- | -- | -- |
+| A | - | 16 | 12 | 21 | - | - | - |
+| B | 16 | - | - | 17 | 20 | - | - |
+| C | 12 | - | - | 28 | - | 31 | - |
+| D | 21 | 17 | 28 | - | 18 | 19 | 23 |
+| E | - | 20 | - | 18 | - | - | 11 |
+| F | - | - | 31 | 19 | - | - | 27 |
+| G | - | - | - | 23 | 11 | 27 | - |
+
+
+However, it is possible to optimise the network by removing some edges and still ensure that all points on the network remain connected. The network which achieves the maximum saving is shown below. It has a weight of 93, representing a saving of 243 − 93 = 150 from the original network.
+
+
+
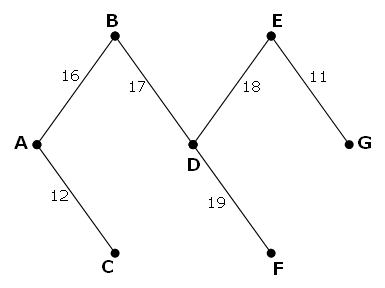+Using `network`, an 2D array representing network in matrix form, find the maximum saving which can be achieved by removing redundant edges whilst ensuring that the network remains connected. Vertices not having connection will be represented with `-1`.
+
+# --hints--
+
+`minimalNetwork(testNetwork)` should return `259679`.
+
+```js
+assert.strictEqual(minimalNetwork(_testNetwork), 259679);
+```
+
+# --seed--
+
+## --after-user-code--
+
+```js
+const _testNetwork = [
+ [-1,-1,-1,427,668,495,377,678,-1,177,-1,-1,870,-1,869,624,300,609,131,-1,251,-1,-1,-1,856,221,514,-1,591,762,182,56,-1,884,412,273,636,-1,-1,774],[-1,-1,262,-1,-1,508,472,799,-1,956,578,363,940,143,-1,162,122,910,-1,729,802,941,922,573,531,539,667,607,-1,920,-1,-1,315,649,937,-1,185,102,636,289],[-1,262,-1,-1,926,-1,958,158,647,47,621,264,81,-1,402,813,649,386,252,391,264,637,349,-1,-1,-1,108,-1,727,225,578,699,-1,898,294,-1,575,168,432,833],[427,-1,-1,-1,366,-1,-1,635,-1,32,962,468,893,854,718,427,448,916,258,-1,760,909,529,311,404,-1,-1,588,680,875,-1,615,-1,409,758,221,-1,-1,76,257],[668,-1,926,366,-1,-1,-1,250,268,-1,503,944,-1,677,-1,727,793,457,981,191,-1,-1,-1,351,969,925,987,328,282,589,-1,873,477,-1,-1,19,450,-1,-1,-1],[495,508,-1,-1,-1,-1,-1,765,711,819,305,302,926,-1,-1,582,-1,861,-1,683,293,-1,-1,66,-1,27,-1,-1,290,-1,786,-1,554,817,33,-1,54,506,386,381],[377,472,958,-1,-1,-1,-1,-1,-1,120,42,-1,134,219,457,639,538,374,-1,-1,-1,966,-1,-1,-1,-1,-1,449,120,797,358,232,550,-1,305,997,662,744,686,239],[678,799,158,635,250,765,-1,-1,-1,35,-1,106,385,652,160,-1,890,812,605,953,-1,-1,-1,79,-1,712,613,312,452,-1,978,900,-1,901,-1,-1,225,533,770,722],[-1,-1,647,-1,268,711,-1,-1,-1,283,-1,172,-1,663,236,36,403,286,986,-1,-1,810,761,574,53,793,-1,-1,777,330,936,883,286,-1,174,-1,-1,-1,828,711],[177,956,47,32,-1,819,120,35,283,-1,50,-1,565,36,767,684,344,489,565,-1,-1,103,810,463,733,665,494,644,863,25,385,-1,342,470,-1,-1,-1,730,582,468],[-1,578,621,962,503,305,42,-1,-1,50,-1,155,519,-1,-1,256,990,801,154,53,474,650,402,-1,-1,-1,966,-1,-1,406,989,772,932,7,-1,823,391,-1,-1,933],[-1,363,264,468,944,302,-1,106,172,-1,155,-1,-1,-1,380,438,-1,41,266,-1,-1,104,867,609,-1,270,861,-1,-1,165,-1,675,250,686,995,366,191,-1,433,-1],[870,940,81,893,-1,926,134,385,-1,565,519,-1,-1,313,851,-1,-1,-1,248,220,-1,826,359,829,-1,234,198,145,409,68,359,-1,814,218,186,-1,-1,929,203,-1],[-1,143,-1,854,677,-1,219,652,663,36,-1,-1,313,-1,132,-1,433,598,-1,-1,168,870,-1,-1,-1,128,437,-1,383,364,966,227,-1,-1,807,993,-1,-1,526,17],[869,-1,402,718,-1,-1,457,160,236,767,-1,380,851,132,-1,-1,596,903,613,730,-1,261,-1,142,379,885,89,-1,848,258,112,-1,900,-1,-1,818,639,268,600,-1],[624,162,813,427,727,582,639,-1,36,684,256,438,-1,-1,-1,-1,539,379,664,561,542,-1,999,585,-1,-1,321,398,-1,-1,950,68,193,-1,697,-1,390,588,848,-1],[300,122,649,448,793,-1,538,890,403,344,990,-1,-1,433,596,539,-1,-1,73,-1,318,-1,-1,500,-1,968,-1,291,-1,-1,765,196,504,757,-1,542,-1,395,227,148],[609,910,386,916,457,861,374,812,286,489,801,41,-1,598,903,379,-1,-1,-1,946,136,399,-1,941,707,156,757,258,251,-1,807,-1,-1,-1,461,501,-1,-1,616,-1],[131,-1,252,258,981,-1,-1,605,986,565,154,266,248,-1,613,664,73,-1,-1,686,-1,-1,575,627,817,282,-1,698,398,222,-1,649,-1,-1,-1,-1,-1,654,-1,-1],[-1,729,391,-1,191,683,-1,953,-1,-1,53,-1,220,-1,730,561,-1,946,686,-1,-1,389,729,553,304,703,455,857,260,-1,991,182,351,477,867,-1,-1,889,217,853],[251,802,264,760,-1,293,-1,-1,-1,-1,474,-1,-1,168,-1,542,318,136,-1,-1,-1,-1,392,-1,-1,-1,267,407,27,651,80,927,-1,974,977,-1,-1,457,117,-1],[-1,941,637,909,-1,-1,966,-1,810,103,650,104,826,870,261,-1,-1,399,-1,389,-1,-1,-1,202,-1,-1,-1,-1,867,140,403,962,785,-1,511,-1,1,-1,707,-1],[-1,922,349,529,-1,-1,-1,-1,761,810,402,867,359,-1,-1,999,-1,-1,575,729,392,-1,-1,388,939,-1,959,-1,83,463,361,-1,-1,512,931,-1,224,690,369,-1],[-1,573,-1,311,351,66,-1,79,574,463,-1,609,829,-1,142,585,500,941,627,553,-1,202,388,-1,164,829,-1,620,523,639,936,-1,-1,490,-1,695,-1,505,109,-1],[856,531,-1,404,969,-1,-1,-1,53,733,-1,-1,-1,-1,379,-1,-1,707,817,304,-1,-1,939,164,-1,-1,616,716,728,-1,889,349,-1,963,150,447,-1,292,586,264],[221,539,-1,-1,925,27,-1,712,793,665,-1,270,234,128,885,-1,968,156,282,703,-1,-1,-1,829,-1,-1,-1,822,-1,-1,-1,736,576,-1,697,946,443,-1,205,194],[514,667,108,-1,987,-1,-1,613,-1,494,966,861,198,437,89,321,-1,757,-1,455,267,-1,959,-1,616,-1,-1,-1,349,156,339,-1,102,790,359,-1,439,938,809,260],[-1,607,-1,588,328,-1,449,312,-1,644,-1,-1,145,-1,-1,398,291,258,698,857,407,-1,-1,620,716,822,-1,-1,293,486,943,-1,779,-1,6,880,116,775,-1,947],[591,-1,727,680,282,290,120,452,777,863,-1,-1,409,383,848,-1,-1,251,398,260,27,867,83,523,728,-1,349,293,-1,212,684,505,341,384,9,992,507,48,-1,-1],[762,920,225,875,589,-1,797,-1,330,25,406,165,68,364,258,-1,-1,-1,222,-1,651,140,463,639,-1,-1,156,486,212,-1,-1,349,723,-1,-1,186,-1,36,240,752],[182,-1,578,-1,-1,786,358,978,936,385,989,-1,359,966,112,950,765,807,-1,991,80,403,361,936,889,-1,339,943,684,-1,-1,965,302,676,725,-1,327,134,-1,147],[56,-1,699,615,873,-1,232,900,883,-1,772,675,-1,227,-1,68,196,-1,649,182,927,962,-1,-1,349,736,-1,-1,505,349,965,-1,474,178,833,-1,-1,555,853,-1],[-1,315,-1,-1,477,554,550,-1,286,342,932,250,814,-1,900,193,504,-1,-1,351,-1,785,-1,-1,-1,576,102,779,341,723,302,474,-1,689,-1,-1,-1,451,-1,-1],[884,649,898,409,-1,817,-1,901,-1,470,7,686,218,-1,-1,-1,757,-1,-1,477,974,-1,512,490,963,-1,790,-1,384,-1,676,178,689,-1,245,596,445,-1,-1,343],[412,937,294,758,-1,33,305,-1,174,-1,-1,995,186,807,-1,697,-1,461,-1,867,977,511,931,-1,150,697,359,6,9,-1,725,833,-1,245,-1,949,-1,270,-1,112],[273,-1,-1,221,19,-1,997,-1,-1,-1,823,366,-1,993,818,-1,542,501,-1,-1,-1,-1,-1,695,447,946,-1,880,992,186,-1,-1,-1,596,949,-1,91,-1,768,273],[636,185,575,-1,450,54,662,225,-1,-1,391,191,-1,-1,639,390,-1,-1,-1,-1,-1,1,224,-1,-1,443,439,116,507,-1,327,-1,-1,445,-1,91,-1,248,-1,344],[-1,102,168,-1,-1,506,744,533,-1,730,-1,-1,929,-1,268,588,395,-1,654,889,457,-1,690,505,292,-1,938,775,48,36,134,555,451,-1,270,-1,248,-1,371,680],[-1,636,432,76,-1,386,686,770,828,582,-1,433,203,526,600,848,227,616,-1,217,117,707,369,109,586,205,809,-1,-1,240,-1,853,-1,-1,-1,768,-1,371,-1,540],[774,289,833,257,-1,381,239,722,711,468,933,-1,-1,17,-1,-1,148,-1,-1,853,-1,-1,-1,-1,264,194,260,947,-1,752,147,-1,-1,343,112,273,344,680,540,-1]
+];
+```
+
+## --seed-contents--
+
+```js
+function minimalNetwork(network) {
+
+ return true;
+}
+
+const testNetwork = [
+ [-1,-1,-1,427,668,495,377,678,-1,177,-1,-1,870,-1,869,624,300,609,131,-1,251,-1,-1,-1,856,221,514,-1,591,762,182,56,-1,884,412,273,636,-1,-1,774],[-1,-1,262,-1,-1,508,472,799,-1,956,578,363,940,143,-1,162,122,910,-1,729,802,941,922,573,531,539,667,607,-1,920,-1,-1,315,649,937,-1,185,102,636,289],[-1,262,-1,-1,926,-1,958,158,647,47,621,264,81,-1,402,813,649,386,252,391,264,637,349,-1,-1,-1,108,-1,727,225,578,699,-1,898,294,-1,575,168,432,833],[427,-1,-1,-1,366,-1,-1,635,-1,32,962,468,893,854,718,427,448,916,258,-1,760,909,529,311,404,-1,-1,588,680,875,-1,615,-1,409,758,221,-1,-1,76,257],[668,-1,926,366,-1,-1,-1,250,268,-1,503,944,-1,677,-1,727,793,457,981,191,-1,-1,-1,351,969,925,987,328,282,589,-1,873,477,-1,-1,19,450,-1,-1,-1],[495,508,-1,-1,-1,-1,-1,765,711,819,305,302,926,-1,-1,582,-1,861,-1,683,293,-1,-1,66,-1,27,-1,-1,290,-1,786,-1,554,817,33,-1,54,506,386,381],[377,472,958,-1,-1,-1,-1,-1,-1,120,42,-1,134,219,457,639,538,374,-1,-1,-1,966,-1,-1,-1,-1,-1,449,120,797,358,232,550,-1,305,997,662,744,686,239],[678,799,158,635,250,765,-1,-1,-1,35,-1,106,385,652,160,-1,890,812,605,953,-1,-1,-1,79,-1,712,613,312,452,-1,978,900,-1,901,-1,-1,225,533,770,722],[-1,-1,647,-1,268,711,-1,-1,-1,283,-1,172,-1,663,236,36,403,286,986,-1,-1,810,761,574,53,793,-1,-1,777,330,936,883,286,-1,174,-1,-1,-1,828,711],[177,956,47,32,-1,819,120,35,283,-1,50,-1,565,36,767,684,344,489,565,-1,-1,103,810,463,733,665,494,644,863,25,385,-1,342,470,-1,-1,-1,730,582,468],[-1,578,621,962,503,305,42,-1,-1,50,-1,155,519,-1,-1,256,990,801,154,53,474,650,402,-1,-1,-1,966,-1,-1,406,989,772,932,7,-1,823,391,-1,-1,933],[-1,363,264,468,944,302,-1,106,172,-1,155,-1,-1,-1,380,438,-1,41,266,-1,-1,104,867,609,-1,270,861,-1,-1,165,-1,675,250,686,995,366,191,-1,433,-1],[870,940,81,893,-1,926,134,385,-1,565,519,-1,-1,313,851,-1,-1,-1,248,220,-1,826,359,829,-1,234,198,145,409,68,359,-1,814,218,186,-1,-1,929,203,-1],[-1,143,-1,854,677,-1,219,652,663,36,-1,-1,313,-1,132,-1,433,598,-1,-1,168,870,-1,-1,-1,128,437,-1,383,364,966,227,-1,-1,807,993,-1,-1,526,17],[869,-1,402,718,-1,-1,457,160,236,767,-1,380,851,132,-1,-1,596,903,613,730,-1,261,-1,142,379,885,89,-1,848,258,112,-1,900,-1,-1,818,639,268,600,-1],[624,162,813,427,727,582,639,-1,36,684,256,438,-1,-1,-1,-1,539,379,664,561,542,-1,999,585,-1,-1,321,398,-1,-1,950,68,193,-1,697,-1,390,588,848,-1],[300,122,649,448,793,-1,538,890,403,344,990,-1,-1,433,596,539,-1,-1,73,-1,318,-1,-1,500,-1,968,-1,291,-1,-1,765,196,504,757,-1,542,-1,395,227,148],[609,910,386,916,457,861,374,812,286,489,801,41,-1,598,903,379,-1,-1,-1,946,136,399,-1,941,707,156,757,258,251,-1,807,-1,-1,-1,461,501,-1,-1,616,-1],[131,-1,252,258,981,-1,-1,605,986,565,154,266,248,-1,613,664,73,-1,-1,686,-1,-1,575,627,817,282,-1,698,398,222,-1,649,-1,-1,-1,-1,-1,654,-1,-1],[-1,729,391,-1,191,683,-1,953,-1,-1,53,-1,220,-1,730,561,-1,946,686,-1,-1,389,729,553,304,703,455,857,260,-1,991,182,351,477,867,-1,-1,889,217,853],[251,802,264,760,-1,293,-1,-1,-1,-1,474,-1,-1,168,-1,542,318,136,-1,-1,-1,-1,392,-1,-1,-1,267,407,27,651,80,927,-1,974,977,-1,-1,457,117,-1],[-1,941,637,909,-1,-1,966,-1,810,103,650,104,826,870,261,-1,-1,399,-1,389,-1,-1,-1,202,-1,-1,-1,-1,867,140,403,962,785,-1,511,-1,1,-1,707,-1],[-1,922,349,529,-1,-1,-1,-1,761,810,402,867,359,-1,-1,999,-1,-1,575,729,392,-1,-1,388,939,-1,959,-1,83,463,361,-1,-1,512,931,-1,224,690,369,-1],[-1,573,-1,311,351,66,-1,79,574,463,-1,609,829,-1,142,585,500,941,627,553,-1,202,388,-1,164,829,-1,620,523,639,936,-1,-1,490,-1,695,-1,505,109,-1],[856,531,-1,404,969,-1,-1,-1,53,733,-1,-1,-1,-1,379,-1,-1,707,817,304,-1,-1,939,164,-1,-1,616,716,728,-1,889,349,-1,963,150,447,-1,292,586,264],[221,539,-1,-1,925,27,-1,712,793,665,-1,270,234,128,885,-1,968,156,282,703,-1,-1,-1,829,-1,-1,-1,822,-1,-1,-1,736,576,-1,697,946,443,-1,205,194],[514,667,108,-1,987,-1,-1,613,-1,494,966,861,198,437,89,321,-1,757,-1,455,267,-1,959,-1,616,-1,-1,-1,349,156,339,-1,102,790,359,-1,439,938,809,260],[-1,607,-1,588,328,-1,449,312,-1,644,-1,-1,145,-1,-1,398,291,258,698,857,407,-1,-1,620,716,822,-1,-1,293,486,943,-1,779,-1,6,880,116,775,-1,947],[591,-1,727,680,282,290,120,452,777,863,-1,-1,409,383,848,-1,-1,251,398,260,27,867,83,523,728,-1,349,293,-1,212,684,505,341,384,9,992,507,48,-1,-1],[762,920,225,875,589,-1,797,-1,330,25,406,165,68,364,258,-1,-1,-1,222,-1,651,140,463,639,-1,-1,156,486,212,-1,-1,349,723,-1,-1,186,-1,36,240,752],[182,-1,578,-1,-1,786,358,978,936,385,989,-1,359,966,112,950,765,807,-1,991,80,403,361,936,889,-1,339,943,684,-1,-1,965,302,676,725,-1,327,134,-1,147],[56,-1,699,615,873,-1,232,900,883,-1,772,675,-1,227,-1,68,196,-1,649,182,927,962,-1,-1,349,736,-1,-1,505,349,965,-1,474,178,833,-1,-1,555,853,-1],[-1,315,-1,-1,477,554,550,-1,286,342,932,250,814,-1,900,193,504,-1,-1,351,-1,785,-1,-1,-1,576,102,779,341,723,302,474,-1,689,-1,-1,-1,451,-1,-1],[884,649,898,409,-1,817,-1,901,-1,470,7,686,218,-1,-1,-1,757,-1,-1,477,974,-1,512,490,963,-1,790,-1,384,-1,676,178,689,-1,245,596,445,-1,-1,343],[412,937,294,758,-1,33,305,-1,174,-1,-1,995,186,807,-1,697,-1,461,-1,867,977,511,931,-1,150,697,359,6,9,-1,725,833,-1,245,-1,949,-1,270,-1,112],[273,-1,-1,221,19,-1,997,-1,-1,-1,823,366,-1,993,818,-1,542,501,-1,-1,-1,-1,-1,695,447,946,-1,880,992,186,-1,-1,-1,596,949,-1,91,-1,768,273],[636,185,575,-1,450,54,662,225,-1,-1,391,191,-1,-1,639,390,-1,-1,-1,-1,-1,1,224,-1,-1,443,439,116,507,-1,327,-1,-1,445,-1,91,-1,248,-1,344],[-1,102,168,-1,-1,506,744,533,-1,730,-1,-1,929,-1,268,588,395,-1,654,889,457,-1,690,505,292,-1,938,775,48,36,134,555,451,-1,270,-1,248,-1,371,680],[-1,636,432,76,-1,386,686,770,828,582,-1,433,203,526,600,848,227,616,-1,217,117,707,369,109,586,205,809,-1,-1,240,-1,853,-1,-1,-1,768,-1,371,-1,540],[774,289,833,257,-1,381,239,722,711,468,933,-1,-1,17,-1,-1,148,-1,-1,853,-1,-1,-1,-1,264,194,260,947,-1,752,147,-1,-1,343,112,273,344,680,540,-1]
+];
+
+minimalNetwork(testNetwork);
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-108-diophantine-reciprocals-i.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-108-diophantine-reciprocals-i.md
new file mode 100644
index 00000000000..56fbe532238
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-108-diophantine-reciprocals-i.md
@@ -0,0 +1,48 @@
+---
+id: 5900f3d91000cf542c50feeb
+title: 'Problem 108: Diophantine Reciprocals I'
+challengeType: 1
+forumTopicId: 301732
+dashedName: problem-108-diophantine-reciprocals-i
+---
+
+# --description--
+
+In the following equation x, y, and n are positive integers.
+
+$$\frac{1}{x} + \frac{1}{y} = \frac{1}{n}$$
+
+For `n` = 4 there are exactly three distinct solutions:
+
+$$\begin{align} & \frac{1}{5} + \frac{1}{20} = \frac{1}{4}\\\\
+ \\\\ & \frac{1}{6} + \frac{1}{12} = \frac{1}{4}\\\\
+ \\\\ & \frac{1}{8} + \frac{1}{8} = \frac{1}{4} \end{align}$$
+
+What is the least value of `n` for which the number of distinct solutions exceeds one-thousand?
+
+# --hints--
+
+`diophantineOne()` should return `180180`.
+
+```js
+assert.strictEqual(diophantineOne(), 180180);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function diophantineOne() {
+
+ return true;
+}
+
+diophantineOne();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-109-darts.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-109-darts.md
new file mode 100644
index 00000000000..5064f7e146c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-109-darts.md
@@ -0,0 +1,57 @@
+---
+id: 5900f3db1000cf542c50feec
+title: 'Problem 109: Darts'
+challengeType: 1
+forumTopicId: 301733
+dashedName: problem-109-darts
+---
+
+# --description--
+
+In the game of darts a player throws three darts at a target board which is split into twenty equal sized sections numbered one to twenty.
+
+
+
+The score of a dart is determined by the number of the region that the dart lands in. A dart landing outside the red/green outer ring scores zero. The black and cream regions inside this ring represent single scores. However, the red/green outer ring and middle ring score double and treble scores respectively.
+
+At the center of the board are two concentric circles called the bull region, or bulls-eye. The outer bull is worth 25 points and the inner bull is a double, worth 50 points.
+
+There are many variations of rules but in the most popular game the players will begin with a score of 301 or 501 and the first player to reduce their running total to zero is a winner. However, it is normal to play a "doubles out" system, which means that the player must land a double (including the double bulls-eye at the center of the board) on their final dart to win; any other dart that would reduce their running total to one or lower means the score for that set of three darts is "bust".
+
+When a player is able to finish on their current score it is called a "checkout" and the highest checkout is 170: T20 T20 D25 (two treble 20s and double bull). There are exactly eleven distinct ways to checkout on a score of 6:
+
+$$\begin{array} \text{D3} & & \\\\
+ D1 & D2 & \\\\ S2 & D2 & \\\\
+ D2 & D1 & \\\\ S4 & D1 & \\\\
+ S1 & S1 & D2 \\\\ S1 & T1 & D1 \\\\
+ S1 & S3 & D1 \\\\ D1 & D1 & D1 \\\\
+ D1 & S2 & D1 \\\\ S2 & S2 & D1 \end{array}$$
+
+Note that D1 D2 is considered different from D2 D1 as they finish on different doubles. However, the combination S1 T1 D1 is considered the same as T1 S1 D1. In addition, we shall not include misses in considering combinations; for example, D3 is the same as 0 D3 and 0 0 D3. Incredibly there are 42336 distinct ways of checking out in total. How many distinct ways can a player checkout with a score less than 100?
+
+# --hints--
+
+`darts()` should return `38182`.
+
+```js
+assert.strictEqual(darts(), 38182);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function darts() {
+
+ return true;
+}
+
+darts();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-110-diophantine-reciprocals-ii.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-110-diophantine-reciprocals-ii.md
new file mode 100644
index 00000000000..9bbeb3dd075
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-110-diophantine-reciprocals-ii.md
@@ -0,0 +1,46 @@
+---
+id: 5900f3db1000cf542c50feed
+title: 'Problem 110: Diophantine Reciprocals II'
+challengeType: 1
+forumTopicId: 301735
+dashedName: problem-110-diophantine-reciprocals-ii
+---
+
+# --description--
+
+In the following equation x, y, and n are positive integers.
+
+$$\frac{1}{x} + \frac{1}{y} = \frac{1}{n}$$
+
+It can be verified that when `n` = 1260 there are 113 distinct solutions and this is the least value of `n` for which the total number of distinct solutions exceeds one hundred.
+
+What is the least value of `n` for which the number of distinct solutions exceeds four million?
+
+**Note:** This problem is a much more difficult version of Problem 108 and as it is well beyond the limitations of a brute force approach it requires a clever implementation.
+
+# --hints--
+
+`diophantineTwo()` should return `9350130049860600`.
+
+```js
+assert.strictEqual(diophantineTwo(), 9350130049860600);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function diophantineTwo() {
+
+ return true;
+}
+
+diophantineTwo();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-111-primes-with-runs.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-111-primes-with-runs.md
new file mode 100644
index 00000000000..7f22fbffb6c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-111-primes-with-runs.md
@@ -0,0 +1,61 @@
+---
+id: 5900f3db1000cf542c50feee
+title: 'Problem 111: Primes with runs'
+challengeType: 1
+forumTopicId: 301736
+dashedName: problem-111-primes-with-runs
+---
+
+# --description--
+
+Considering 4-digit primes containing repeated digits it is clear that they cannot all be the same: 1111 is divisible by 11, 2222 is divisible by 22, and so on. But there are nine 4-digit primes containing three ones:
+
+$$1117, 1151, 1171, 1181, 1511, 1811, 2111, 4111, 8111$$
+
+We shall say that $M(n, d)$ represents the maximum number of repeated digits for an n-digit prime where d is the repeated digit, $N(n, d)$ represents the number of such primes, and $S(n, d)$ represents the sum of these primes.
+
+So $M(4, 1) = 3$ is the maximum number of repeated digits for a 4-digit prime where one is the repeated digit, there are $N(4, 1) = 9$ such primes, and the sum of these primes is $S(4, 1) = 22275$. It turns out that for d = 0, it is only possible to have $M(4, 0) = 2$ repeated digits, but there are $N(4, 0) = 13$ such cases.
+
+In the same way we obtain the following results for 4-digit primes.
+
+| Digit, d | $M(4, d)$ | $N(4, d)$ | $S(4, d)$ |
+| -------- | --------- | --------- | --------- |
+| 0 | 2 | 13 | 67061 |
+| 1 | 3 | 9 | 22275 |
+| 2 | 3 | 1 | 2221 |
+| 3 | 3 | 12 | 46214 |
+| 4 | 3 | 2 | 8888 |
+| 5 | 3 | 1 | 5557 |
+| 6 | 3 | 1 | 6661 |
+| 7 | 3 | 9 | 57863 |
+| 8 | 3 | 1 | 8887 |
+| 9 | 3 | 7 | 48073 |
+
+For d = 0 to 9, the sum of all $S(4, d)$ is 273700. Find the sum of all $S(10, d)$.
+
+# --hints--
+
+`primesWithRuns()` should return `612407567715`.
+
+```js
+assert.strictEqual(primesWithRuns(), 612407567715);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primesWithRuns() {
+
+ return true;
+}
+
+primesWithRuns();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-112-bouncy-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-112-bouncy-numbers.md
new file mode 100644
index 00000000000..7599de29978
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-112-bouncy-numbers.md
@@ -0,0 +1,48 @@
+---
+id: 5900f3dd1000cf542c50feef
+title: 'Problem 112: Bouncy numbers'
+challengeType: 1
+forumTopicId: 301738
+dashedName: problem-112-bouncy-numbers
+---
+
+# --description--
+
+Working from left-to-right if no digit is exceeded by the digit to its left it is called an increasing number; for example, 134468.
+
+Similarly if no digit is exceeded by the digit to its right it is called a decreasing number; for example, 66420.
+
+We shall call a positive integer that is neither increasing nor decreasing a "bouncy" number; for example, 155349.
+
+Clearly there cannot be any bouncy numbers below one-hundred, but just over half of the numbers below one-thousand (525) are bouncy. In fact, the least number for which the proportion of bouncy numbers first reaches 50% is 538.
+
+Surprisingly, bouncy numbers become more and more common and by the time we reach 21780 the proportion of bouncy numbers is equal to 90%.
+
+Find the least number for which the proportion of bouncy numbers is exactly 99%.
+
+# --hints--
+
+`bouncyNumbers()` should return `1587000`.
+
+```js
+assert.strictEqual(bouncyNumbers(), 1587000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function bouncyNumbers() {
+
+ return true;
+}
+
+bouncyNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-113-non-bouncy-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-113-non-bouncy-numbers.md
new file mode 100644
index 00000000000..868909ef6b2
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-113-non-bouncy-numbers.md
@@ -0,0 +1,46 @@
+---
+id: 5900f3dd1000cf542c50fef0
+title: 'Problem 113: Non-bouncy numbers'
+challengeType: 1
+forumTopicId: 301739
+dashedName: problem-113-non-bouncy-numbers
+---
+
+# --description--
+
+Working from left-to-right if no digit is exceeded by the digit to its left it is called an increasing number; for example, 134468.
+
+Similarly if no digit is exceeded by the digit to its right it is called a decreasing number; for example, 66420.
+
+We shall call a positive integer that is neither increasing nor decreasing a "bouncy" number; for example, 155349.
+
+As n increases, the proportion of bouncy numbers below n increases such that there are only 12951 numbers below one-million that are not bouncy and only 277032 non-bouncy numbers below ${10}^{10}$.
+
+How many numbers below a googol (${10}^{100}$) are not bouncy?
+
+# --hints--
+
+`nonBouncyNumbers()` should return `51161058134250`.
+
+```js
+assert.strictEqual(nonBouncyNumbers(), 51161058134250);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function nonBouncyNumbers() {
+
+ return true;
+}
+
+nonBouncyNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-114-counting-block-combinations-i.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-114-counting-block-combinations-i.md
new file mode 100644
index 00000000000..3e1b2f85927
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-114-counting-block-combinations-i.md
@@ -0,0 +1,44 @@
+---
+id: 5900f3e01000cf542c50fef2
+title: 'Problem 114: Counting block combinations I'
+challengeType: 1
+forumTopicId: 301740
+dashedName: problem-114-counting-block-combinations-i
+---
+
+# --description--
+
+A row measuring seven units in length has red blocks with a minimum length of three units placed on it, such that any two red blocks (which are allowed to be different lengths) are separated by at least one black square. There are exactly seventeen ways of doing this.
+
+
+
+How many ways can a row measuring fifty units in length be filled?
+
+**Note:** Although the example above does not lend itself to the possibility, in general it is permitted to mix block sizes. For example, on a row measuring eight units in length you could use red (3), black (1), and red (4).
+
+# --hints--
+
+`countingBlockOne()` should return `16475640049`.
+
+```js
+assert.strictEqual(countingBlockOne(), 16475640049);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function countingBlockOne() {
+
+ return true;
+}
+
+countingBlockOne();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-115-counting-block-combinations-ii.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-115-counting-block-combinations-ii.md
new file mode 100644
index 00000000000..a659ea34ad1
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-115-counting-block-combinations-ii.md
@@ -0,0 +1,50 @@
+---
+id: 5900f3df1000cf542c50fef1
+title: 'Problem 115: Counting block combinations II'
+challengeType: 1
+forumTopicId: 301741
+dashedName: problem-115-counting-block-combinations-ii
+---
+
+# --description--
+
+A row measuring `n` units in length has red blocks with a minimum length of `m` units placed on it, such that any two red blocks (which are allowed to be different lengths) are separated by at least one black square.
+
+Let the fill-count function, $F(m, n)$, represent the number of ways that a row can be filled.
+
+For example, $F(3, 29) = 673135$ and $F(3, 30) = 1089155$.
+
+That is, for m = 3, it can be seen that n = 30 is the smallest value for which the fill-count function first exceeds one million.
+
+In the same way, for m = 10, it can be verified that $F(10, 56) = 880711$ and $F(10, 57) = 1148904$, so n = 57 is the least value for which the fill-count function first exceeds one million.
+
+For m = 50, find the least value of `n` for which the fill-count function first exceeds one million.
+
+**Note:** This is a more difficult version of Problem 114.
+
+# --hints--
+
+`countingBlockTwo()` should return `168`.
+
+```js
+assert.strictEqual(countingBlockTwo(), 168);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function countingBlockTwo() {
+
+ return true;
+}
+
+countingBlockTwo();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-116-red-green-or-blue-tiles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-116-red-green-or-blue-tiles.md
new file mode 100644
index 00000000000..b0b1969a3df
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-116-red-green-or-blue-tiles.md
@@ -0,0 +1,54 @@
+---
+id: 5900f3e01000cf542c50fef3
+title: 'Problem 116: Red, green or blue tiles'
+challengeType: 1
+forumTopicId: 301742
+dashedName: problem-116-red-green-or-blue-tiles
+---
+
+# --description--
+
+A row of five black square tiles is to have a number of its tiles replaced with coloured oblong tiles chosen from red (length two), green (length three), or blue (length four).
+
+If red tiles are chosen there are exactly seven ways this can be done.
+
+
+
+If green tiles are chosen there are three ways.
+
+
+
+And if blue tiles are chosen there are two ways.
+
+
+
+Assuming that colors cannot be mixed there are 7 + 3 + 2 = 12 ways of replacing the black tiles in a row measuring five units in length. How many different ways can the black tiles in a row measuring fifty units in length be replaced if colors cannot be mixed and at least one colored tile must be used?
+
+**Note:** This is related to Problem 117.
+
+# --hints--
+
+`redGreenBlueOne()` should return `20492570929`.
+
+```js
+assert.strictEqual(redGreenBlueOne(), 20492570929);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function redGreenBlueOne() {
+
+ return true;
+}
+
+redGreenBlueOne();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-117-red-green-and-blue-tiles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-117-red-green-and-blue-tiles.md
new file mode 100644
index 00000000000..4a4873aac95
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-117-red-green-and-blue-tiles.md
@@ -0,0 +1,44 @@
+---
+id: 5900f3e21000cf542c50fef4
+title: 'Problem 117: Red, green, and blue tiles'
+challengeType: 1
+forumTopicId: 301743
+dashedName: problem-117-red-green-and-blue-tiles
+---
+
+# --description--
+
+Using a combination of black square tiles and oblong tiles chosen from: red tiles measuring two units, green tiles measuring three units, and blue tiles measuring four units, it is possible to tile a row measuring five units in length in exactly fifteen different ways.
+
+
+
+How many ways can a row measuring fifty units in length be tiled?
+
+**Note**: This is related to Problem 116.
+
+# --hints--
+
+`redGreenBlueTilesTwo()` should return `100808458960497`.
+
+```js
+assert.strictEqual(redGreenBlueTilesTwo(), 100808458960497);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function redGreenBlueTilesTwo() {
+
+ return true;
+}
+
+redGreenBlueTilesTwo();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-118-pandigital-prime-sets.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-118-pandigital-prime-sets.md
new file mode 100644
index 00000000000..195d39136ed
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-118-pandigital-prime-sets.md
@@ -0,0 +1,40 @@
+---
+id: 5900f3e21000cf542c50fef5
+title: 'Problem 118: Pandigital prime sets'
+challengeType: 1
+forumTopicId: 301744
+dashedName: problem-118-pandigital-prime-sets
+---
+
+# --description--
+
+Using all of the digits 1 through 9 and concatenating them freely to form decimal integers, different sets can be formed. Interestingly with the set $\\{2, 5, 47, 89, 631\\}$, all of the elements belonging to it are prime.
+
+How many distinct sets containing each of the digits one through nine exactly once contain only prime elements?
+
+# --hints--
+
+`pandigitalPrimeSets()` should return `44680`.
+
+```js
+assert.strictEqual(pandigitalPrimeSets(), 44680);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pandigitalPrimeSets() {
+
+ return true;
+}
+
+pandigitalPrimeSets();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-119-digit-power-sum.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-119-digit-power-sum.md
new file mode 100644
index 00000000000..87bf836b33a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-119-digit-power-sum.md
@@ -0,0 +1,44 @@
+---
+id: 5900f3e41000cf542c50fef6
+title: 'Problem 119: Digit power sum'
+challengeType: 1
+forumTopicId: 301745
+dashedName: problem-119-digit-power-sum
+---
+
+# --description--
+
+The number 512 is interesting because it is equal to the sum of its digits raised to some power: $5 + 1 + 2 = 8$, and $8^3 = 512$. Another example of a number with this property is $614656 = 28^4$.
+
+We shall define $a_n$ to be the $n-th$ term of this sequence and insist that a number must contain at least two digits to have a sum.
+
+You are given that $a_2 = 512$ and $a_{10} = 614656$.
+
+Find $a_{30}$.
+
+# --hints--
+
+`digitPowerSum()` should return `248155780267521`.
+
+```js
+assert.strictEqual(digitPowerSum(), 248155780267521);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function digitPowerSum() {
+
+ return true;
+}
+
+digitPowerSum();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-120-square-remainders.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-120-square-remainders.md
new file mode 100644
index 00000000000..d42c224e3db
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-120-square-remainders.md
@@ -0,0 +1,42 @@
+---
+id: 5900f3e41000cf542c50fef7
+title: 'Problem 120: Square remainders'
+challengeType: 1
+forumTopicId: 301747
+dashedName: problem-120-square-remainders
+---
+
+# --description--
+
+Let `r` be the remainder when ${(a − 1)}^n + {(a + 1)}^n$ is divided by $a^2$.
+
+For example, if $a = 7$ and $n = 3$, then $r = 42: 6^3 + 8^3 = 728 ≡ 42 \\ \text{mod}\\ 49$. And as `n` varies, so too will `r`, but for $a = 7$ it turns out that $r_{max} = 42$.
+
+For $3 ≤ a ≤ 1000$, find $\sum{r}_{max}$.
+
+# --hints--
+
+`squareRemainders()` should return `333082500`.
+
+```js
+assert.strictEqual(squareRemainders(), 333082500);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function squareRemainders() {
+
+ return true;
+}
+
+squareRemainders();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-121-disc-game-prize-fund.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-121-disc-game-prize-fund.md
new file mode 100644
index 00000000000..0f23b7fdd50
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-121-disc-game-prize-fund.md
@@ -0,0 +1,44 @@
+---
+id: 5900f3e51000cf542c50fef8
+title: 'Problem 121: Disc game prize fund'
+challengeType: 1
+forumTopicId: 301748
+dashedName: problem-121-disc-game-prize-fund
+---
+
+# --description--
+
+A bag contains one red disc and one blue disc. In a game of chance a player takes a disc at random and its colour is noted. After each turn the disc is returned to the bag, an extra red disc is added, and another disc is taken at random.
+
+The player pays £1 to play and wins if they have taken more blue discs than red discs at the end of the game.
+
+If the game is played for four turns, the probability of a player winning is exactly 11/120, and so the maximum prize fund the banker should allocate for winning in this game would be £10 before they would expect to incur a loss. Note that any payout will be a whole number of pounds and also includes the original £1 paid to play the game, so in the example given the player actually wins £9.
+
+Find the maximum prize fund that should be allocated to a single game in which fifteen turns are played.
+
+# --hints--
+
+`discGamePrize()` should return `2269`.
+
+```js
+assert.strictEqual(discGamePrize(), 2269);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function discGamePrize() {
+
+ return true;
+}
+
+discGamePrize();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-122-efficient-exponentiation.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-122-efficient-exponentiation.md
new file mode 100644
index 00000000000..78c29aa7952
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-122-efficient-exponentiation.md
@@ -0,0 +1,57 @@
+---
+id: 5900f3e61000cf542c50fef9
+title: 'Problem 122: Efficient exponentiation'
+challengeType: 1
+forumTopicId: 301749
+dashedName: problem-122-efficient-exponentiation
+---
+
+# --description--
+
+The most naive way of computing $n^{15}$ requires fourteen multiplications:
+
+$$n × n × \ldots × n = n^{15}$$
+
+But using a "binary" method you can compute it in six multiplications:
+
+$$\begin{align} & n × n = n^2\\\\
+ & n^2 × n^2 = n^4\\\\ & n^4 × n^4 = n^8\\\\
+ & n^8 × n^4 = n^{12}\\\\ & n^{12} × n^2 = n^{14}\\\\
+ & n^{14} × n = n^{15} \end{align}$$
+
+However it is yet possible to compute it in only five multiplications:
+
+$$\begin{align} & n × n = n^2\\\\
+ & n^2 × n = n^3\\\\ & n^3 × n^3 = n^6\\\\
+ & n^6 × n^6 = n^{12}\\\\ & n^{12} × n^3 = n^{15} \end{align}$$
+
+We shall define $m(k)$ to be the minimum number of multiplications to compute $n^k$; for example $m(15) = 5$.
+
+For $1 ≤ k ≤ 200$, find $\sum{m(k)}$.
+
+# --hints--
+
+`efficientExponentation()` should return `1582`.
+
+```js
+assert.strictEqual(efficientExponentation(), 1582);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function efficientExponentation() {
+
+ return true;
+}
+
+efficientExponentation();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-123-prime-square-remainders.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-123-prime-square-remainders.md
new file mode 100644
index 00000000000..743089b64e3
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-123-prime-square-remainders.md
@@ -0,0 +1,44 @@
+---
+id: 5900f3e71000cf542c50fefa
+title: 'Problem 123: Prime square remainders'
+challengeType: 1
+forumTopicId: 301750
+dashedName: problem-123-prime-square-remainders
+---
+
+# --description--
+
+Let $p_n$ be the $n$th prime: 2, 3, 5, 7, 11, ..., and let $r$ be the remainder when ${(p_n−1)}^n + {(p_n+1)}^n$ is divided by ${p_n}^2$.
+
+For example, when $n = 3, p_3 = 5$, and $4^3 + 6^3 = 280 ≡ 5\\ mod\\ 25$.
+
+The least value of $n$ for which the remainder first exceeds $10^9$ is 7037.
+
+Find the least value of $n$ for which the remainder first exceeds $10^{10}$.
+
+# --hints--
+
+`primeSquareRemainders()` should return `21035`.
+
+```js
+assert.strictEqual(primeSquareRemainders(), 21035);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeSquareRemainders() {
+
+ return true;
+}
+
+primeSquareRemainders();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-124-ordered-radicals.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-124-ordered-radicals.md
new file mode 100644
index 00000000000..899171a9731
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-124-ordered-radicals.md
@@ -0,0 +1,142 @@
+---
+id: 5900f3e81000cf542c50fefb
+title: 'Problem 124: Ordered radicals'
+challengeType: 1
+forumTopicId: 301751
+dashedName: problem-124-ordered-radicals
+---
+
+# --description--
+
+The radical of $n$, $rad(n)$, is the product of the distinct prime factors of $n$. For example, $504 = 2^3 × 3^2 × 7$, so $rad(504) = 2 × 3 × 7 = 42$.
+
+If we calculate $rad(n)$ for $1 ≤ n ≤ 10$, then sort them on $rad(n)$, and sorting on $n$ if the radical values are equal, we get:
+
+
+
+
+
+
| $Unsorted$ | ++ | $Sorted$ | +|||
| $n$ | +$rad(n)$ | ++ | $n$ | +$rad(n)$ | +$k$ | +
| 1 | +1 | ++ | 1 | +1 | +1 | +
| 2 | +2 | ++ | 2 | +2 | +2 | +
| 3 | +3 | ++ | 4 | +2 | +3 | +
| 4 | +2 | ++ | 8 | +2 | +4 | +
| 5 | +5 | ++ | 3 | +3 | +5 | +
| 6 | +6 | ++ | 9 | +3 | +6 | +
| 7 | +7 | ++ | 5 | +5 | +7 | +
| 8 | +2 | ++ | 6 | +6 | +8 | +
| 9 | +3 | ++ | 7 | +7 | +9 | +
| 10 | +10 | ++ | 10 | +10 | +10 | +
+ +Let $E(k)$ be the $k$th element in the sorted $n$ column; for example, $E(4) = 8$ and $E(6) = 9$. If $rad(n)$ is sorted for $1 ≤ n ≤ 100000$, find $E(10000)$. + +# --hints-- + +`orderedRadicals()` should return `21417`. + +```js +assert.strictEqual(orderedRadicals(), 21417); +``` + +# --seed-- + +## --seed-contents-- + +```js +function orderedRadicals() { + + return true; +} + +orderedRadicals(); +``` + +# --solutions-- + +```js +// solution required +``` diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-125-palindromic-sums.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-125-palindromic-sums.md new file mode 100644 index 00000000000..eb499c13931 --- /dev/null +++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-125-palindromic-sums.md @@ -0,0 +1,79 @@ +--- +id: 5900f3e91000cf542c50fefc +title: 'Problem 125: Palindromic sums' +challengeType: 1 +forumTopicId: 301752 +dashedName: problem-125-palindromic-sums +--- + +# --description-- + +The palindromic number 595 is interesting because it can be written as the sum of consecutive squares: $6^2 + 7^2 + 8^2 + 9^2 + 10^2 + 11^2 + 12^2$. + +There are exactly eleven palindromes below one-thousand that can be written as consecutive square sums, and the sum of these palindromes is 4164. Note that $1 = 0^2 + 1^2$ has not been included as this problem is concerned with the squares of positive integers. + +Find the sum of all the numbers less than the `limit` that are both palindromic and can be written as the sum of consecutive squares. + +# --hints-- +`palindromicSums(100000000)` should return `2906969179`. + +```js + +assert.strictEqual(palindromicSums(100000000), 2906969179); + +``` + +`palindromicSums(100)` should return `137`. + +```js +assert.strictEqual(palindromicSums(100), 137); +``` + +`palindromicSums(1000)` should return `4164`. + +```js +assert.strictEqual(palindromicSums(1000),4164); +``` + +# --seed-- + +## --seed-contents-- + +```js +function palindromicSums(limit) { + + return true; +} + +palindromicSums(100); +``` + +# --solutions-- + +```js +function isPalindrome(num) { + return num + .toString() + .split('') + .every((digit, i, arr) => digit === arr[arr.length - 1 - i]); +} + +function palindromicSums(limit) { + let sumOfPalindromes = 0; + const sqrtLimit = Math.sqrt(limit); + const list = new Set(); + + for (let i = 1; i <= sqrtLimit; i++) { + let sumOfSquares = i * i; + for (let j = i + 1; j <= sqrtLimit; j++) { + sumOfSquares += j * j; + if (sumOfSquares > limit) break; + if (isPalindrome(sumOfSquares) && !list.has(sumOfSquares)) { + sumOfPalindromes += sumOfSquares; + list.add(sumOfSquares); + } + } + } + return sumOfPalindromes; +} +``` diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-126-cuboid-layers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-126-cuboid-layers.md new file mode 100644 index 00000000000..d089c18aff0 --- /dev/null +++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-126-cuboid-layers.md @@ -0,0 +1,50 @@ +--- +id: 5900f3ea1000cf542c50fefd +title: 'Problem 126: Cuboid layers' +challengeType: 1 +forumTopicId: 301753 +dashedName: problem-126-cuboid-layers +--- + +# --description-- + +The minimum number of cubes to cover every visible face on a cuboid measuring 3 x 2 x 1 is twenty-two. + +
+
+If we add a second layer to this solid it would require forty-six cubes to cover every visible face, the third layer would require seventy-eight cubes, and the fourth layer would require one-hundred and eighteen cubes to cover every visible face.
+
+However, the first layer on a cuboid measuring 5 x 1 x 1 also requires twenty-two cubes; similarly, the first layer on cuboids measuring 5 x 3 x 1, 7 x 2 x 1, and 11 x 1 x 1 all contain forty-six cubes.
+
+We shall define $C(n)$ to represent the number of cuboids that contain $n$ cubes in one of its layers. So $C(22) = 2$, $C(46) = 4$, $C(78) = 5$, and $C(118) = 8$.
+
+It turns out that 154 is the least value of $n$ for which $C(n) = 10$.
+
+Find the least value of $n$ for which $C(n) = 1000$.
+
+# --hints--
+
+`cuboidLayers()` should return `18522`.
+
+```js
+assert.strictEqual(cuboidLayers(), 18522);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function cuboidLayers() {
+
+ return true;
+}
+
+cuboidLayers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-127-abc-hits.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-127-abc-hits.md
new file mode 100644
index 00000000000..2f7f927858e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-127-abc-hits.md
@@ -0,0 +1,56 @@
+---
+id: 5900f3ec1000cf542c50fefe
+title: 'Problem 127: abc-hits'
+challengeType: 1
+forumTopicId: 301754
+dashedName: problem-127-abc-hits
+---
+
+# --description--
+
+The radical of $n$, $rad(n)$, is the product of distinct prime factors of $n$. For example, $504 = 2^3 × 3^2 × 7$, so $rad(504) = 2 × 3 × 7 = 42$.
+
+We shall define the triplet of positive integers (a, b, c) to be an abc-hit if:
+
+1. $GCD(a, b) = GCD(a, c) = GCD(b, c) = 1$
+2. $a < b$
+3. $a + b = c$
+4. $rad(abc) < c$
+
+For example, (5, 27, 32) is an abc-hit, because:
+
+1. $GCD(5, 27) = GCD(5, 32) = GCD(27, 32) = 1$
+2. $5 < 27$
+3. $5 + 27 = 32$
+4. $rad(4320) = 30 < 32$
+
+It turns out that abc-hits are quite rare and there are only thirty-one abc-hits for $c < 1000$, with $\sum{c} = 12523$.
+
+Find $\sum{c}$ for $c < 120000$.
+
+# --hints--
+
+`abcHits()` should return `18407904`.
+
+```js
+assert.strictEqual(abcHits(), 18407904);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function abcHits() {
+
+ return true;
+}
+
+abcHits();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-128-hexagonal-tile-differences.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-128-hexagonal-tile-differences.md
new file mode 100644
index 00000000000..49d59948762
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-128-hexagonal-tile-differences.md
@@ -0,0 +1,117 @@
+---
+id: 5900f3ec1000cf542c50feff
+title: 'Problem 128: Hexagonal tile differences'
+challengeType: 1
+forumTopicId: 301755
+dashedName: problem-128-hexagonal-tile-differences
+---
+
+# --description--
+
+A hexagonal tile with number 1 is surrounded by a ring of six hexagonal tiles, starting at "12 o'clock" and numbering the tiles 2 to 7 in an anti-clockwise direction.
+
+New rings are added in the same fashion, with the next rings being numbered 8 to 19, 20 to 37, 38 to 61, and so on. The diagram below shows the first three rings.
+
+
+
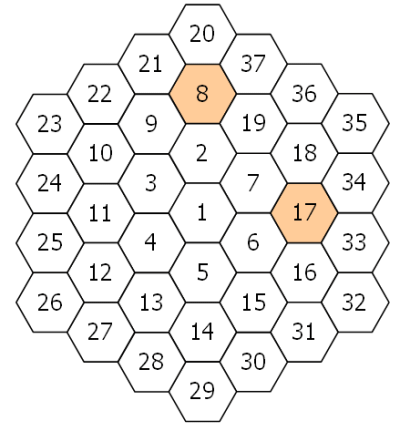+By finding the difference between tile $n$ and each of its six neighbours we shall define $PD(n)$ to be the number of those differences which are prime.
+
+For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So $PD(8) = 3$.
+
+In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence $PD(17) = 2$.
+
+It can be shown that the maximum value of $PD(n)$ is $3$.
+
+If all of the tiles for which $PD(n) = 3$ are listed in ascending order to form a sequence, the 10th tile would be 271.
+
+Find the 2000th tile in this sequence.
+
+# --hints--
+
+`hexagonalTile(10)` should return `271`.
+
+```js
+assert.strictEqual(hexagonalTile(10), 271);
+```
+
+`hexagonalTile(2000)` should return `14516824220`.
+
+```js
+assert.strictEqual(hexagonalTile(2000), 14516824220);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function hexagonalTile(tileIndex) {
+
+ return true;
+}
+
+hexagonalTile(10);
+```
+
+# --solutions--
+
+```js
+class PrimeSeive {
+ constructor(num) {
+ const seive = Array(Math.floor((num - 1) / 2)).fill(true);
+ const upper = Math.floor((num - 1) / 2);
+ const sqrtUpper = Math.floor((Math.sqrt(num) - 1) / 2);
+
+ for (let i = 0; i <= sqrtUpper; i++) {
+ if (seive[i]) {
+ // Mark value in seive array
+ const prime = 2 * i + 3;
+ // Mark all multiples of this number as false (not prime)
+ const primeSqaredIndex = 2 * i ** 2 + 6 * i + 3;
+ for (let j = primeSqaredIndex; j < upper; j += prime) {
+ seive[j] = false;
+ }
+ }
+ }
+
+ this._seive = seive;
+ }
+
+ isPrime(num) {
+ return num === 2
+ ? true
+ : num % 2 === 0
+ ? false
+ : this.isOddPrime(num);
+ }
+
+ isOddPrime(num) {
+ return this._seive[(num - 3) / 2];
+ }
+};
+
+function hexagonalTile(tileIndex) {
+ const primeSeive = new PrimeSeive(tileIndex * 420);
+ let count = 1;
+ let n = 1;
+ let number = 0;
+
+ while (count < tileIndex) {
+ if (primeSeive.isPrime(6*n - 1) &&
+ primeSeive.isPrime(6*n + 1) &&
+ primeSeive.isPrime(12*n + 5)) {
+ number = 3*n*n - 3*n + 2;
+ count++;
+ if (count >= tileIndex) break;
+ }
+ if (primeSeive.isPrime(6*n + 5) &&
+ primeSeive.isPrime(6*n - 1) &&
+ primeSeive.isPrime(12*n - 7) && n != 1) {
+ number = 3*n*n + 3*n + 1;
+ count++;
+ }
+ n++;
+ }
+ return number;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-129-repunit-divisibility.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-129-repunit-divisibility.md
new file mode 100644
index 00000000000..e7f423f96d5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-129-repunit-divisibility.md
@@ -0,0 +1,44 @@
+---
+id: 5900f3ef1000cf542c50ff01
+title: 'Problem 129: Repunit divisibility'
+challengeType: 1
+forumTopicId: 301756
+dashedName: problem-129-repunit-divisibility
+---
+
+# --description--
+
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
+
+Given that $n$ is a positive integer and $GCD(n, 10) = 1$, it can be shown that there always exists a value, $k$, for which $R(k)$ is divisible by $n$, and let $A(n)$ be the least such value of $k$; for example, $A(7) = 6$ and $A(41) = 5$.
+
+The least value of $n$ for which $A(n)$ first exceeds ten is 17.
+
+Find the least value of $n$ for which $A(n)$ first exceeds one-million.
+
+# --hints--
+
+`repunitDivisibility()` should return `1000023`.
+
+```js
+assert.strictEqual(repunitDivisibility(), 1000023);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function repunitDivisibility() {
+
+ return true;
+}
+
+repunitDivisibility();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-130-composites-with-prime-repunit-property.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-130-composites-with-prime-repunit-property.md
new file mode 100644
index 00000000000..48f7149e5a6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-130-composites-with-prime-repunit-property.md
@@ -0,0 +1,46 @@
+---
+id: 5900f3ee1000cf542c50ff00
+title: 'Problem 130: Composites with prime repunit property'
+challengeType: 1
+forumTopicId: 301758
+dashedName: problem-130-composites-with-prime-repunit-property
+---
+
+# --description--
+
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
+
+Given that $n$ is a positive integer and $GCD(n, 10) = 1$, it can be shown that there always exists a value, $k$, for which $R(k)$ is divisible by $n$, and let $A(n)$ be the least such value of $k$; for example, $A(7) = 6$ and $A(41) = 5$.
+
+You are given that for all primes, $p > 5$, that $p − 1$ is divisible by $A(p)$. For example, when $p = 41, A(41) = 5$, and 40 is divisible by 5.
+
+However, there are rare composite values for which this is also true; the first five examples being 91, 259, 451, 481, and 703.
+
+Find the sum of the first twenty-five composite values of $n$ for which $GCD(n, 10) = 1$ and $n − 1$ is divisible by $A(n)$.
+
+# --hints--
+
+`compositeRepunit()` should return `149253`.
+
+```js
+assert.strictEqual(compositeRepunit(), 149253);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function compositeRepunit() {
+
+ return true;
+}
+
+compositeRepunit();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-131-prime-cube-partnership.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-131-prime-cube-partnership.md
new file mode 100644
index 00000000000..73e7e8e7490
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-131-prime-cube-partnership.md
@@ -0,0 +1,44 @@
+---
+id: 5900f3ef1000cf542c50ff02
+title: 'Problem 131: Prime cube partnership'
+challengeType: 1
+forumTopicId: 301759
+dashedName: problem-131-prime-cube-partnership
+---
+
+# --description--
+
+There are some prime values, $p$, for which there exists a positive integer, $n$, such that the expression $n^3 + n^{2}p$ is a perfect cube.
+
+For example, when $p = 19,\\ 8^3 + 8^2 × 19 = {12}^3$.
+
+What is perhaps most surprising is that the value of $n$ is unique for each prime with this property, and there are only four such primes below one hundred.
+
+How many primes below one million have this remarkable property?
+
+# --hints--
+
+`primeCubePartnership()` should return `173`.
+
+```js
+assert.strictEqual(primeCubePartnership(), 173);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeCubePartnership() {
+
+ return true;
+}
+
+primeCubePartnership();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-132-large-repunit-factors.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-132-large-repunit-factors.md
new file mode 100644
index 00000000000..5ca7c0760fd
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-132-large-repunit-factors.md
@@ -0,0 +1,42 @@
+---
+id: 5900f3f11000cf542c50ff03
+title: 'Problem 132: Large repunit factors'
+challengeType: 1
+forumTopicId: 301760
+dashedName: problem-132-large-repunit-factors
+---
+
+# --description--
+
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$.
+
+For example, $R(10) = 1111111111 = 11 × 41 × 271 × 9091$, and the sum of these prime factors is 9414.
+
+Find the sum of the first forty prime factors of $R({10}^9)$.
+
+# --hints--
+
+`largeRepunitFactors()` should return `843296`.
+
+```js
+assert.strictEqual(largeRepunitFactors(), 843296);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function largeRepunitFactors() {
+
+ return true;
+}
+
+largeRepunitFactors();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-133-repunit-nonfactors.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-133-repunit-nonfactors.md
new file mode 100644
index 00000000000..ee861a14420
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-133-repunit-nonfactors.md
@@ -0,0 +1,44 @@
+---
+id: 5900f3f21000cf542c50ff04
+title: 'Problem 133: Repunit nonfactors'
+challengeType: 1
+forumTopicId: 301761
+dashedName: problem-133-repunit-nonfactors
+---
+
+# --description--
+
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
+
+Let us consider repunits of the form $R({10}^n)$.
+
+Although $R(10)$, $R(100)$, or $R(1000)$ are not divisible by 17, $R(10000)$ is divisible by 17. Yet there is no value of n for which $R({10}^n)$ will divide by 19. Remarkably, 11, 17, 41, and 73 are the only four primes below one-hundred that can be a factor of $R({10}^n)$.
+
+Find the sum of all the primes below one-hundred thousand that will never be a factor of $R({10}^n)$.
+
+# --hints--
+
+`repunitNonfactors()` should return `453647705`.
+
+```js
+assert.strictEqual(repunitNonfactors(), 453647705);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function repunitNonfactors() {
+
+ return true;
+}
+
+repunitNonfactors();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-134-prime-pair-connection.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-134-prime-pair-connection.md
new file mode 100644
index 00000000000..d6629ef1579
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-134-prime-pair-connection.md
@@ -0,0 +1,42 @@
+---
+id: 5900f3f21000cf542c50ff05
+title: 'Problem 134: Prime pair connection'
+challengeType: 1
+forumTopicId: 301762
+dashedName: problem-134-prime-pair-connection
+---
+
+# --description--
+
+Consider the consecutive primes $p_1 = 19$ and $p_2 = 23$. It can be verified that 1219 is the smallest number such that the last digits are formed by $p_1$ whilst also being divisible by $p_2$.
+
+In fact, with the exception of $p_1 = 3$ and $p_2 = 5$, for every pair of consecutive primes, $p_2 > p_1$, there exist values of $n$ for which the last digits are formed by $p_1$ and $n$ is divisible by $p_2$. Let $S$ be the smallest of these values of $n$.
+
+Find $\sum{S}$ for every pair of consecutive primes with $5 ≤ p_1 ≤ 1000000$.
+
+# --hints--
+
+`primePairConnection()` should return `18613426663617120`.
+
+```js
+assert.strictEqual(primePairConnection(), 18613426663617120);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primePairConnection() {
+
+ return true;
+}
+
+primePairConnection();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-135-same-differences.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-135-same-differences.md
new file mode 100644
index 00000000000..3045467d61e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-135-same-differences.md
@@ -0,0 +1,44 @@
+---
+id: 5900f3f31000cf542c50ff06
+title: 'Problem 135: Same differences'
+challengeType: 1
+forumTopicId: 301763
+dashedName: problem-135-same-differences
+---
+
+# --description--
+
+Given the positive integers, $x$, $y$, and $z$, are consecutive terms of an arithmetic progression, the least value of the positive integer, $n$, for which the equation, $x^2 − y^2 − z^2 = n$, has exactly two solutions is $n = 27$:
+
+$$34^2 − 27^2 − 20^2 = 12^2 − 9^2 − 6^2 = 27$$
+
+It turns out that $n = 1155$ is the least value which has exactly ten solutions.
+
+How many values of $n$ less than one million have exactly ten distinct solutions?
+
+# --hints--
+
+`sameDifferences()` should return `4989`.
+
+```js
+assert.strictEqual(sameDifferences(), 4989);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sameDifferences() {
+
+ return true;
+}
+
+sameDifferences();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-136-singleton-difference.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-136-singleton-difference.md
new file mode 100644
index 00000000000..d73ff59f63b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-136-singleton-difference.md
@@ -0,0 +1,44 @@
+---
+id: 5900f3f51000cf542c50ff07
+title: 'Problem 136: Singleton difference'
+challengeType: 1
+forumTopicId: 301764
+dashedName: problem-136-singleton-difference
+---
+
+# --description--
+
+The positive integers, $x$, $y$, and $z$, are consecutive terms of an arithmetic progression. Given that $n$ is a positive integer, the equation, $x^2 − y^2 − z^2 = n$, has exactly one solution when $n = 20$:
+
+$$13^2 − 10^2 − 7^2 = 20$$
+
+In fact, there are twenty-five values of $n$ below one hundred for which the equation has a unique solution.
+
+How many values of $n$ less than fifty million have exactly one solution?
+
+# --hints--
+
+`singletonDifference()` should return `2544559`.
+
+```js
+assert.strictEqual(singletonDifference(), 2544559);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function singletonDifference() {
+
+ return true;
+}
+
+singletonDifference();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-137-fibonacci-golden-nuggets.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-137-fibonacci-golden-nuggets.md
new file mode 100644
index 00000000000..b700dba62d0
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-137-fibonacci-golden-nuggets.md
@@ -0,0 +1,59 @@
+---
+id: 5900f3f51000cf542c50ff08
+title: 'Problem 137: Fibonacci golden nuggets'
+challengeType: 1
+forumTopicId: 301765
+dashedName: problem-137-fibonacci-golden-nuggets
+---
+
+# --description--
+
+Consider the infinite polynomial series $A_{F}(x) = xF_1 + x^2F_2 + x^3F_3 + \ldots$, where $F_k$ is the $k$th term in the Fibonacci sequence: $1, 1, 2, 3, 5, 8, \ldots$; that is, $F_k = F_{k − 1} + F_{k − 2}, F_1 = 1$ and $F_2 = 1$.
+
+For this problem we shall be interested in values of $x$ for which $A_{F}(x)$ is a positive integer.
+
+Surprisingly
+
+$$\begin{align} A_F(\frac{1}{2}) & = (\frac{1}{2}) × 1 + {(\frac{1}{2})}^2 × 1 + {(\frac{1}{2})}^3 × 2 + {(\frac{1}{2})}^4 × 3 + {(\frac{1}{2})}^5 × 5 + \cdots \\\\
+ & = \frac{1}{2} + \frac{1}{4} + \frac{2}{8} + \frac{3}{16} + \frac{5}{32} + \cdots \\\\ & = 2 \end{align}$$
+
+The corresponding values of $x$ for the first five natural numbers are shown below.
+
+| $x$ | $A_F(x)$ |
+| --------------------------- | -------- |
+| $\sqrt{2} − 1$ | $1$ |
+| $\frac{1}{2}$ | $2$ |
+| $\frac{\sqrt{13} − 2}{3}$ | $3$ |
+| $\frac{\sqrt{89} − 5}{8}$ | $4$ |
+| $\frac{\sqrt{34} − 3}{5}$ | $5$ |
+
+We shall call $A_F(x)$ a golden nugget if $x$ is rational, because they become increasingly rarer; for example, the 10th golden nugget is 74049690.
+
+Find the 15th golden nugget.
+
+# --hints--
+
+`goldenNugget()` should return `1120149658760`.
+
+```js
+assert.strictEqual(goldenNugget(), 1120149658760);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function goldenNugget() {
+
+ return true;
+}
+
+goldenNugget();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-138-special-isosceles-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-138-special-isosceles-triangles.md
new file mode 100644
index 00000000000..6391b7523c4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-138-special-isosceles-triangles.md
@@ -0,0 +1,46 @@
+---
+id: 5900f3f61000cf542c50ff09
+title: 'Problem 138: Special isosceles triangles'
+challengeType: 1
+forumTopicId: 301766
+dashedName: problem-138-special-isosceles-triangles
+---
+
+# --description--
+
+Consider the isosceles triangle with base length, $b = 16$, and legs, $L = 17$.
+
+
+
+By using the Pythagorean theorem, it can be seen that the height of the triangle, $h = \sqrt{{17}^2 − 8^2} = 15$, which is one less than the base length.
+
+With $b = 272$ and $L = 305$, we get $h = 273$, which is one more than the base length, and this is the second smallest isosceles triangle with the property that $h = b ± 1$.
+
+Find $\sum{L}$ for the twelve smallest isosceles triangles for which $h = b ± 1$ and $b$, $L$ are positive integers.
+
+# --hints--
+
+`isoscelesTriangles()` should return `1118049290473932`.
+
+```js
+assert.strictEqual(isoscelesTriangles(), 1118049290473932);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function isoscelesTriangles() {
+
+ return true;
+}
+
+isoscelesTriangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-139-pythagorean-tiles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-139-pythagorean-tiles.md
new file mode 100644
index 00000000000..19f12579cb2
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-139-pythagorean-tiles.md
@@ -0,0 +1,46 @@
+---
+id: 5900f3f71000cf542c50ff0a
+title: 'Problem 139: Pythagorean tiles'
+challengeType: 1
+forumTopicId: 301767
+dashedName: problem-139-pythagorean-tiles
+---
+
+# --description--
+
+Let (a, b, c) represent the three sides of a right angle triangle with integral length sides. It is possible to place four such triangles together to form a square with length c.
+
+For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.
+
+
+
+However, if (5, 12, 13) triangles were used, the hole would measure 7 by 7. These 7 by 7 squares could not be used to tile the 13 by 13 square.
+
+Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to occur?
+
+# --hints--
+
+`pythagoreanTiles()` should return `10057761`.
+
+```js
+assert.strictEqual(pythagoreanTiles(), 10057761);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pythagoreanTiles() {
+
+ return true;
+}
+
+pythagoreanTiles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-140-modified-fibonacci-golden-nuggets.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-140-modified-fibonacci-golden-nuggets.md
new file mode 100644
index 00000000000..bdd6612a63c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-140-modified-fibonacci-golden-nuggets.md
@@ -0,0 +1,52 @@
+---
+id: 5900f3fa1000cf542c50ff0c
+title: 'Problem 140: Modified Fibonacci golden nuggets'
+challengeType: 1
+forumTopicId: 301769
+dashedName: problem-140-modified-fibonacci-golden-nuggets
+---
+
+# --description--
+
+Consider the infinite polynomial series $A_G(x) = xG_1 + x^2G_2 + x^3G_3 + \cdots$, where $G_k$ is the $k$th term of the second order recurrence relation $G_k = G_{k − 1} + G_{k − 2}, G_1 = 1$ and $G_2 = 4$; that is, $1, 4, 5, 9, 14, 23, \ldots$.
+
+For this problem we shall be concerned with values of $x$ for which $A_G(x)$ is a positive integer.
+
+The corresponding values of $x$ for the first five natural numbers are shown below.
+
+| $x$ | $A_G(x)$ |
+| ----------------------------- | -------- |
+| $\frac{\sqrt{5} − 1}{4}$ | $1$ |
+| $\frac{2}{5}$ | $2$ |
+| $\frac{\sqrt{22} − 2}{6}$ | $3$ |
+| $\frac{\sqrt{137} − 5}{14}$ | $4$ |
+| $\frac{1}{2}$ | $5$ |
+
+We shall call $A_G(x)$ a golden nugget if $x$ is rational because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
+
+# --hints--
+
+`modifiedGoldenNuggets()` should return `5673835352990`
+
+```js
+assert.strictEqual(modifiedGoldenNuggets(), 5673835352990);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function modifiedGoldenNuggets() {
+
+ return true;
+}
+
+modifiedGoldenNuggets();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-141-investigating-progressive-numbers-n-which-are-also-square.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-141-investigating-progressive-numbers-n-which-are-also-square.md
new file mode 100644
index 00000000000..9f1e9d3bb45
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-141-investigating-progressive-numbers-n-which-are-also-square.md
@@ -0,0 +1,46 @@
+---
+id: 5900f3f91000cf542c50ff0b
+title: 'Problem 141: Investigating progressive numbers, n, which are also square'
+challengeType: 1
+forumTopicId: 301770
+dashedName: problem-141-investigating-progressive-numbers-n-which-are-also-square
+---
+
+# --description--
+
+A positive integer, $n$, is divided by $d$ and the quotient and remainder are $q$ and $r$ respectively. In addition $d$, $q$, and $r$ are consecutive positive integer terms in a geometric sequence, but not necessarily in that order.
+
+For example, 58 divided by 6 has a quotient of 9 and a remainder of 4. It can also be seen that 4, 6, 9 are consecutive terms in a geometric sequence (common ratio $\frac{3}{2}$).
+
+We will call such numbers, $n$, progressive.
+
+Some progressive numbers, such as 9 and 10404 = ${102}^2$, also happen to be perfect squares. The sum of all progressive perfect squares below one hundred thousand is 124657.
+
+Find the sum of all progressive perfect squares below one trillion (${10}^{12}$).
+
+# --hints--
+
+`progressivePerfectSquares()` should return `878454337159`.
+
+```js
+assert.strictEqual(progressivePerfectSquares(), 878454337159);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function progressivePerfectSquares() {
+
+ return true;
+}
+
+progressivePerfectSquares();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-142-perfect-square-collection.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-142-perfect-square-collection.md
new file mode 100644
index 00000000000..17a07958833
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-142-perfect-square-collection.md
@@ -0,0 +1,38 @@
+---
+id: 5900f3fa1000cf542c50ff0d
+title: 'Problem 142: Perfect Square Collection'
+challengeType: 1
+forumTopicId: 301771
+dashedName: problem-142-perfect-square-collection
+---
+
+# --description--
+
+Find the smallest $x + y + z$ with integers $x > y > z > 0$ such that $x + y$, $x − y$, $x + z$, $x − z$, $y + z$, $y − z$ are all perfect squares.
+
+# --hints--
+
+`perfectSquareCollection()` should return `1006193`.
+
+```js
+assert.strictEqual(perfectSquareCollection(), 1006193);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function perfectSquareCollection() {
+
+ return true;
+}
+
+perfectSquareCollection();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-143-investigating-the-torricelli-point-of-a-triangle.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-143-investigating-the-torricelli-point-of-a-triangle.md
new file mode 100644
index 00000000000..8051dd4317d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-143-investigating-the-torricelli-point-of-a-triangle.md
@@ -0,0 +1,46 @@
+---
+id: 5900f3fc1000cf542c50ff0e
+title: 'Problem 143: Investigating the Torricelli point of a triangle'
+challengeType: 1
+forumTopicId: 301772
+dashedName: problem-143-investigating-the-torricelli-point-of-a-triangle
+---
+
+# --description--
+
+Let ABC be a triangle with all interior angles being less than 120 degrees. Let X be any point inside the triangle and let $XA = p$, $XC = q$, and $XB = r$.
+
+Fermat challenged Torricelli to find the position of X such that p + q + r was minimised.
+
+Torricelli was able to prove that if equilateral triangles AOB, BNC and AMC are constructed on each side of triangle ABC, the circumscribed circles of AOB, BNC, and AMC will intersect at a single point, T, inside the triangle. Moreover he proved that T, called the Torricelli/Fermat point, minimises $p + q + r$. Even more remarkable, it can be shown that when the sum is minimised, $AN = BM = CO = p + q + r$ and that AN, BM and CO also intersect at T.
+
+
+
+If the sum is minimised and a, b, c, p, q and r are all positive integers we shall call triangle ABC a Torricelli triangle. For example, $a = 399$, $b = 455$, $c = 511$ is an example of a Torricelli triangle, with $p + q + r = 784$. Find the sum of all distinct values of $p + q + r ≤ 120000$ for Torricelli triangles.
+
+# --hints--
+
+`sumTorricelliTriangles()` should return `30758397`.
+
+```js
+assert.strictEqual(sumTorricelliTriangles(), 30758397);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumTorricelliTriangles() {
+
+ return true;
+}
+
+sumTorricelliTriangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-144-investigating-multiple-reflections-of-a-laser-beam.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-144-investigating-multiple-reflections-of-a-laser-beam.md
new file mode 100644
index 00000000000..935df9d895d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-144-investigating-multiple-reflections-of-a-laser-beam.md
@@ -0,0 +1,61 @@
+---
+id: 5900f3fc1000cf542c50ff0f
+title: 'Problem 144: Investigating multiple reflections of a laser beam'
+challengeType: 1
+forumTopicId: 301773
+dashedName: problem-144-investigating-multiple-reflections-of-a-laser-beam
+---
+
+# --description--
+
+In laser physics, a "white cell" is a mirror system that acts as a delay line for the laser beam. The beam enters the cell, bounces around on the mirrors, and eventually works its way back out.
+
+The specific white cell we will be considering is an ellipse with the equation $4{x}^2 + y^2 = 100$
+
+The section corresponding to $−0.01 ≤ x ≤ +0.01$ at the top is missing, allowing the light to enter and exit through the hole.
+
+
+ 
+ 
+
+
++ +The light beam in this problem starts at the point (0.0, 10.1) just outside the white cell, and the beam first impacts the mirror at (1.4, -9.6). + +Each time the laser beam hits the surface of the ellipse, it follows the usual law of reflection "angle of incidence equals angle of reflection." That is, both the incident and reflected beams make the same angle with the normal line at the point of incidence. + +In the figure on the left, the red line shows the first two points of contact between the laser beam and the wall of the white cell; the blue line shows the line tangent to the ellipse at the point of incidence of the first bounce. + +The slope m of the tangent line at any point (x, y) of the given ellipse is: $m = −4 × \frac{x}{y}$ + +The normal line is perpendicular to this tangent line at the point of incidence. + +The animation on the right shows the first 10 reflections of the beam. + +How many times does the beam hit the internal surface of the white cell before exiting? + +# --hints-- + +`laserBeamReflections()` should return `354`. + +```js +assert.strictEqual(laserBeamReflections(), 354); +``` + +# --seed-- + +## --seed-contents-- + +```js +function laserBeamReflections() { + + return true; +} + +laserBeamReflections(); +``` + +# --solutions-- + +```js +// solution required +``` diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-145-how-many-reversible-numbers-are-there-below-one-billion.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-145-how-many-reversible-numbers-are-there-below-one-billion.md new file mode 100644 index 00000000000..f30799446b2 --- /dev/null +++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-145-how-many-reversible-numbers-are-there-below-one-billion.md @@ -0,0 +1,42 @@ +--- +id: 5900f3fd1000cf542c50ff10 +title: 'Problem 145: How many reversible numbers are there below one-billion?' +challengeType: 1 +forumTopicId: 301774 +dashedName: problem-145-how-many-reversible-numbers-are-there-below-one-billion +--- + +# --description-- + +Some positive integers $n$ have the property that the sum [ $n + reverse(n)$ ] consists entirely of odd (decimal) digits. For instance, $36 + 63 = 99$ and $409 + 904 = 1313$. We will call such numbers reversible; so 36, 63, 409, and 904 are reversible. Leading zeroes are not allowed in either $n$ or $reverse(n)$. + +There are 120 reversible numbers below one-thousand. + +How many reversible numbers are there below one-billion (${10}^9$)? + +# --hints-- + +`reversibleNumbers()` should return `608720`. + +```js +assert.strictEqual(reversibleNumbers(), 608720); +``` + +# --seed-- + +## --seed-contents-- + +```js +function reversibleNumbers() { + + return true; +} + +reversibleNumbers(); +``` + +# --solutions-- + +```js +// solution required +``` diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-146-investigating-a-prime-pattern.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-146-investigating-a-prime-pattern.md new file mode 100644 index 00000000000..6407520a81a --- /dev/null +++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-146-investigating-a-prime-pattern.md @@ -0,0 +1,40 @@ +--- +id: 5900f3fe1000cf542c50ff11 +title: 'Problem 146: Investigating a Prime Pattern' +challengeType: 1 +forumTopicId: 301775 +dashedName: problem-146-investigating-a-prime-pattern +--- + +# --description-- + +The smallest positive integer $n$ for which the numbers $n^2 + 1$, $n^2 + 3$, $n^2 + 7$, $n^2 + 9$, $n^2 + 13$, and $n^2 + 27$ are consecutive primes is 10. The sum of all such integers $n$ below one-million is 1242490. + +What is the sum of all such integers $n$ below 150 million? + +# --hints-- + +`primePattern()` should return `676333270`. + +```js +assert.strictEqual(primePattern(), 676333270); +``` + +# --seed-- + +## --seed-contents-- + +```js +function primePattern() { + + return true; +} + +primePattern(); +``` + +# --solutions-- + +```js +// solution required +``` diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-147-rectangles-in-cross-hatched-grids.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-147-rectangles-in-cross-hatched-grids.md new file mode 100644 index 00000000000..dfade844910 --- /dev/null +++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-147-rectangles-in-cross-hatched-grids.md @@ -0,0 +1,48 @@ +--- +id: 5900f3ff1000cf542c50ff12 +title: 'Problem 147: Rectangles in cross-hatched grids' +challengeType: 1 +forumTopicId: 301776 +dashedName: problem-147-rectangles-in-cross-hatched-grids +--- + +# --description-- + +In a 3x2 cross-hatched grid, a total of 37 different rectangles could be situated within that grid as indicated in the sketch. + +
+
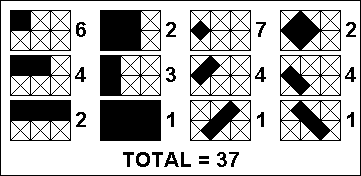+There are 5 grids smaller than 3x2, vertical and horizontal dimensions being important, i.e. 1x1, 2x1, 3x1, 1x2 and 2x2. If each of them is cross-hatched, the following number of different rectangles could be situated within those smaller grids:
+
+$$\begin{array}{|c|c|} \hline 1 \times 1 & 1 \\\\ \hline 2 \times 1 & 4 \\\\ \hline 3 \times 1 & 8 \\\\ \hline 1 \times 2 & 4 \\\\ \hline 2 \times 2 & 18 \\\\ \hline \end{array}$$
+
+Adding those to the 37 of the 3x2 grid, a total of 72 different rectangles could be situated within 3x2 and smaller grids.
+
+How many different rectangles could be situated within 47x43 and smaller grids?
+
+# --hints--
+
+`crossHatchedRectangles()` should return `846910284`.
+
+```js
+assert.strictEqual(crossHatchedRectangles(), 846910284);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function crossHatchedRectangles() {
+
+ return true;
+}
+
+crossHatchedRectangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-148-exploring-pascals-triangle.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-148-exploring-pascals-triangle.md
new file mode 100644
index 00000000000..d30e62b5442
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-148-exploring-pascals-triangle.md
@@ -0,0 +1,54 @@
+---
+id: 5900f4021000cf542c50ff14
+title: 'Problem 148: Exploring Pascal''s triangle'
+challengeType: 1
+forumTopicId: 301777
+dashedName: problem-148-exploring-pascals-triangle
+---
+
+# --description--
+
+We can easily verify that none of the entries in the first seven rows of Pascal's triangle are divisible by 7:
+
+```markup
+ 1
+ 1 1
+ 1 2 1
+ 1 3 3 1
+ 1 4 6 4 1
+ 1 5 10 10 5 1
+1 6 15 20 15 6 1
+```
+
+However, if we check the first one hundred rows, we will find that only 2361 of the 5050 entries are not divisible by 7.
+
+# --instructions--
+
+Find the number of entries which are not divisible by 7 in the first one billion (${10}^9$) rows of Pascal's triangle.
+
+# --hints--
+
+`entriesOfPascalsTriangle()` should return `2129970655314432`.
+
+```js
+assert.strictEqual(entriesOfPascalsTriangle(), 2129970655314432);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function entriesOfPascalsTriangle() {
+
+ return true;
+}
+
+entriesOfPascalsTriangle();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-149-searching-for-a-maximum-sum-subsequence.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-149-searching-for-a-maximum-sum-subsequence.md
new file mode 100644
index 00000000000..c1fbd34962d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-149-searching-for-a-maximum-sum-subsequence.md
@@ -0,0 +1,54 @@
+---
+id: 5900f4021000cf542c50ff13
+title: 'Problem 149: Searching for a maximum-sum subsequence'
+challengeType: 1
+forumTopicId: 301778
+dashedName: problem-149-searching-for-a-maximum-sum-subsequence
+---
+
+# --description--
+
+Looking at the table below, it is easy to verify that the maximum possible sum of adjacent numbers in any direction (horizontal, vertical, diagonal or anti-diagonal) is $16 (= 8 + 7 + 1)$.
+
+$$\begin{array}{|r|r|r|r|} \hline −2 & 5 & 3 & 2 \\\\ \hline 9 & −6 & 5 & 1 \\\\ \hline 3 & 2 & 7 & 3 \\\\ \hline −1 & 8 & −4 & 8 \\\\ \hline \end{array}$$
+
+Now, let us repeat the search, but on a much larger scale:
+
+First, generate four million pseudo-random numbers using a specific form of what is known as a "Lagged Fibonacci Generator":
+
+For $1 ≤ k ≤ 55$, $s_k = (100003 − 200003k + 300007{k}^3) \\ (modulo\\ 1000000) − 500000$.
+
+For $56 ≤ k ≤ 4000000$, $s_k = (s_{k − 24} + s_{k − 55} + 1000000) \\ (modulo\\ 1000000) − 500000$.
+
+Thus, $s_{10} = −393027$ and $s_{100} = 86613$.
+
+The terms of $s$ are then arranged in a 2000×2000 table, using the first 2000 numbers to fill the first row (sequentially), the next 2000 numbers to fill the second row, and so on.
+
+Finally, find the greatest sum of (any number of) adjacent entries in any direction (horizontal, vertical, diagonal or anti-diagonal).
+
+# --hints--
+
+`maximumSubSequence()` should return `52852124`.
+
+```js
+assert.strictEqual(maximumSubSequence(), 52852124);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function maximumSubSequence() {
+
+ return true;
+}
+
+maximumSubSequence();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-150-searching-a-triangular-array-for-a-sub-triangle-having-minimum-sum.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-150-searching-a-triangular-array-for-a-sub-triangle-having-minimum-sum.md
new file mode 100644
index 00000000000..366d5dd9bd0
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-150-searching-a-triangular-array-for-a-sub-triangle-having-minimum-sum.md
@@ -0,0 +1,63 @@
+---
+id: 5900f4031000cf542c50ff15
+title: >-
+ Problem 150: Searching a triangular array for a sub-triangle having minimum-sum
+challengeType: 1
+forumTopicId: 301781
+dashedName: problem-150-searching-a-triangular-array-for-a-sub-triangle-having-minimum-sum
+---
+
+# --description--
+
+In a triangular array of positive and negative integers, we wish to find a sub-triangle such that the sum of the numbers it contains is the smallest possible.
+
+In the example below, it can be easily verified that the marked triangle satisfies this condition having a sum of −42.
+
+
+
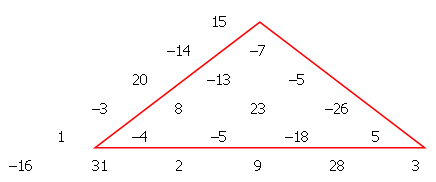+We wish to make such a triangular array with one thousand rows, so we generate 500500 pseudo-random numbers $s_k$ in the range $±2^{19}$, using a type of random number generator (known as a Linear Congruential Generator) as follows:
+
+$$\begin{align} t := & \\ 0\\\\
+ \text{for}\\ & k = 1\\ \text{up to}\\ k = 500500:\\\\ & t := (615949 × t + 797807)\\ \text{modulo}\\ 2^{20}\\\\
+ & s_k := t − 219\\\\ \end{align}$$
+
+Thus: $s_1 = 273519$, $s_2 = −153582$, $s_3 = 450905$ etc.
+
+Our triangular array is then formed using the pseudo-random numbers thus:
+
+$$ s_1 \\\\
+s_2\\;s_3 \\\\ s_4\\; s_5\\; s_6 \\\\
+s_7\\; s_8\\; s_9\\; s_{10} \\\\ \ldots $$
+
+Sub-triangles can start at any element of the array and extend down as far as we like (taking-in the two elements directly below it from the next row, the three elements directly below from the row after that, and so on).
+
+The "sum of a sub-triangle" is defined as the sum of all the elements it contains.
+
+Find the smallest possible sub-triangle sum.
+
+# --hints--
+
+`smallestSubTriangleSum()` should return `-271248680`.
+
+```js
+assert.strictEqual(smallestSubTriangleSum(), -271248680);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function smallestSubTriangleSum() {
+
+ return true;
+}
+
+smallestSubTriangleSum();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-151-paper-sheets-of-standard-sizes-an-expected-value-problem.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-151-paper-sheets-of-standard-sizes-an-expected-value-problem.md
new file mode 100644
index 00000000000..47f785ed97b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-151-paper-sheets-of-standard-sizes-an-expected-value-problem.md
@@ -0,0 +1,52 @@
+---
+id: 5900f4031000cf542c50ff16
+title: 'Problem 151: Paper sheets of standard sizes: an expected-value problem'
+challengeType: 1
+forumTopicId: 301782
+dashedName: problem-151-paper-sheets-of-standard-sizes-an-expected-value-problem
+---
+
+# --description--
+
+A printing shop runs 16 batches (jobs) every week and each batch requires a sheet of special colour-proofing paper of size A5.
+
+Every Monday morning, the foreman opens a new envelope, containing a large sheet of the special paper with size A1.
+
+He proceeds to cut it in half, thus getting two sheets of size A2. Then he cuts one of them in half to get two sheets of size A3 and so on until he obtains the A5-size sheet needed for the first batch of the week.
+
+All the unused sheets are placed back in the envelope.
+
+
+
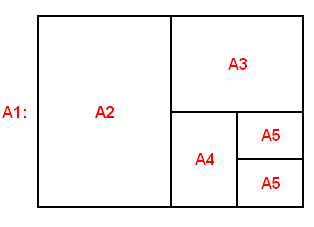+At the beginning of each subsequent batch, he takes one sheet of paper from the envelope at random. If it is of size A5, he uses it. If it is larger, he repeats the 'cut-in-half' procedure until he has what he needs, and any remaining sheets are always placed back in the envelope.
+
+Excluding the first and last batch of the week, find the expected number of times (during each week) that the foreman finds a single sheet of paper in the envelope.
+
+Give your answer rounded to six decimal places using the format `x.xxxxxx`.
+
+# --hints--
+
+`expectedValueProblem()` should return `0.464399`.
+
+```js
+assert.strictEqual(expectedValueProblem(), 0.464399);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function expectedValueProblem() {
+
+ return true;
+}
+
+expectedValueProblem();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-152-writing-one-half-as-a-sum-of-inverse-squares.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-152-writing-one-half-as-a-sum-of-inverse-squares.md
new file mode 100644
index 00000000000..c03197b781f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-152-writing-one-half-as-a-sum-of-inverse-squares.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4041000cf542c50ff17
+title: 'Problem 152: Writing one half as a sum of inverse squares'
+challengeType: 1
+forumTopicId: 301783
+dashedName: problem-152-writing-one-half-as-a-sum-of-inverse-squares
+---
+
+# --description--
+
+There are several ways to write the number $\frac{1}{2}$ as a sum of inverse squares using distinct integers.
+
+For instance, the numbers {2,3,4,5,7,12,15,20,28,35} can be used:
+
+$$\frac{1}{2} = \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \frac{1}{7^2} + \frac{1}{{12}^2} + \frac{1}{{15}^2} + \frac{1}{{20}^2} + \frac{1}{{28}^2} + \frac{1}{{35}^2}$$
+
+In fact, only using integers between 2 and 45 inclusive, there are exactly three ways to do it, the remaining two being: {2,3,4,6,7,9,10,20,28,35,36,45} and {2,3,4,6,7,9,12,15,28,30,35,36,45}.
+
+How many ways are there to write the number $\frac{1}{2}$ as a sum of inverse squares using distinct integers between 2 and 80 inclusive?
+
+# --hints--
+
+`sumInverseSquares()` should return `301`.
+
+```js
+assert.strictEqual(sumInverseSquares(), 301);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumInverseSquares() {
+
+ return true;
+}
+
+sumInverseSquares();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-153-investigating-gaussian-integers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-153-investigating-gaussian-integers.md
new file mode 100644
index 00000000000..a66c05c4f97
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-153-investigating-gaussian-integers.md
@@ -0,0 +1,84 @@
+---
+id: 5900f4051000cf542c50ff18
+title: 'Problem 153: Investigating Gaussian Integers'
+challengeType: 1
+forumTopicId: 301784
+dashedName: problem-153-investigating-gaussian-integers
+---
+
+# --description--
+
+As we all know the equation $x^2 = -1$ has no solutions for real $x$.
+
+If we however introduce the imaginary number $i$ this equation has two solutions: $x = i$ and $x = -i$.
+
+If we go a step further the equation ${(x - 3)}^2 = -4$ has two complex solutions: $x = 3 + 2i$ and $x = 3 - 2i$, which are called each others' complex conjugate.
+
+Numbers of the form $a + bi$ are called complex numbers.
+
+In general $a + bi$ and $a − bi$ are each other's complex conjugate. A Gaussian Integer is a complex number $a + bi$ such that both $a$ and $b$ are integers.
+
+The regular integers are also Gaussian integers (with $b = 0$).
+
+To distinguish them from Gaussian integers with $b ≠ 0$ we call such integers "rational integers."
+
+A Gaussian integer is called a divisor of a rational integer $n$ if the result is also a Gaussian integer.
+
+If for example we divide 5 by $1 + 2i$ we can simplify in the following manner:
+
+Multiply numerator and denominator by the complex conjugate of $1 + 2i$: $1 − 2i$.
+
+The result is:
+
+$$\frac{5}{1 + 2i} = \frac{5}{1 + 2i} \frac{1 - 2i}{1 - 2i} = \frac{5(1 - 2i)}{1 - {(2i)}^2} = \frac{5(1 - 2i)}{1 - (-4)} = \frac{5(1 - 2i)}{5} = 1 - 2i$$
+
+So $1 + 2i$ is a divisor of 5.
+
+Note that $1 + i$ is not a divisor of 5 because:
+
+$$\frac{5}{1 + i} = \frac{5}{2} - \frac{5}{2}i$$
+
+Note also that if the Gaussian Integer ($a + bi$) is a divisor of a rational integer $n$, then its complex conjugate ($a − bi$) is also a divisor of $n$. In fact, 5 has six divisors such that the real part is positive: {1, 1 + 2i, 1 − 2i, 2 + i, 2 − i, 5}.
+
+The following is a table of all of the divisors for the first five positive rational integers:
+
+| n | Gaussian integer divisors with positive real part | Sum s(n) of these divisors |
+| - | ------------------------------------------------- | -------------------------- |
+| 1 | 1 | 1 |
+| 2 | 1, 1 + i, 1 - i, 2 | 5 |
+| 3 | 1, 3 | 4 |
+| 4 | 1, 1 + i, 1 - i, 2, 2 + 2i, 2 - 2i, 4 | 13 |
+| 5 | 1, 1 + 2i, 1 - 2i, 2 + i, 2 - i, 5 | 12 |
+
+For divisors with positive real parts, then, we have: $\displaystyle\sum_{n=1}^5 s(n) = 35$.
+
+For $1 ≤ n ≤ {10}^5$, $\displaystyle\sum_{n = 1}^{{10}^5} s(n) = 17924657155$.
+
+What is $\displaystyle\sum_{n=1}^{{10}^8} s(n)$?
+
+# --hints--
+
+`sumGaussianIntegers()` should return `17971254122360636`.
+
+```js
+assert.strictEqual(sumGaussianIntegers(), 17971254122360636);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumGaussianIntegers() {
+
+ return true;
+}
+
+sumGaussianIntegers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-154-exploring-pascals-pyramid.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-154-exploring-pascals-pyramid.md
new file mode 100644
index 00000000000..40533ba38f8
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-154-exploring-pascals-pyramid.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4071000cf542c50ff19
+title: 'Problem 154: Exploring Pascal''s pyramid'
+challengeType: 1
+forumTopicId: 301785
+dashedName: problem-154-exploring-pascals-pyramid
+---
+
+# --description--
+
+A triangular pyramid is constructed using spherical balls so that each ball rests on exactly three balls of the next lower level.
+
+
+
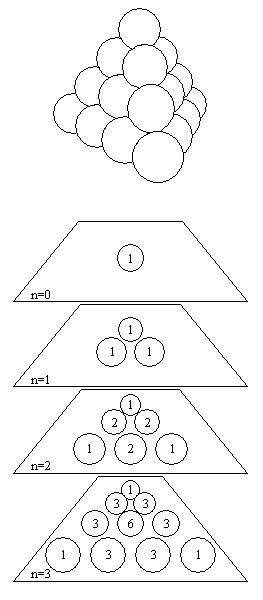+Then, we calculate the number of paths leading from the apex to each position: A path starts at the apex and progresses downwards to any of the three spheres directly below the current position. Consequently, the number of paths to reach a certain position is the sum of the numbers immediately above it (depending on the position, there are up to three numbers above it).
+
+The result is Pascal's pyramid and the numbers at each level n are the coefficients of the trinomial expansion ${(x + y + z)}^n$.
+
+How many coefficients in the expansion of ${(x + y + z)}^{200000}$ are multiples of ${10}^{12}$?
+
+# --hints--
+
+`pascalsPyramid()` should return `479742450`.
+
+```js
+assert.strictEqual(pascalsPyramid(), 479742450);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pascalsPyramid() {
+
+ return true;
+}
+
+pascalsPyramid();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-155-counting-capacitor-circuits.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-155-counting-capacitor-circuits.md
new file mode 100644
index 00000000000..ee1b1f97d9b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-155-counting-capacitor-circuits.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4081000cf542c50ff1a
+title: 'Problem 155: Counting Capacitor Circuits'
+challengeType: 1
+forumTopicId: 301786
+dashedName: problem-155-counting-capacitor-circuits
+---
+
+# --description--
+
+An electric circuit uses exclusively identical capacitors of the same value C.
+
+The capacitors can be connected in series or in parallel to form sub-units, which can then be connected in series or in parallel with other capacitors or other sub-units to form larger sub-units, and so on up to a final circuit.
+
+Using this simple procedure and up to n identical capacitors, we can make circuits having a range of different total capacitances. For example, using up to $n = 3$ capacitors of $60 μF$ each, we can obtain the following 7 distinct total capacitance values:
+
+
+
+If we denote by $D(n)$ the number of distinct total capacitance values we can obtain when using up to $n$ equal-valued capacitors and the simple procedure described above, we have: $D(1) = 1, D(2) = 3, D(3)=7, \ldots$
+
+Find $D(18)$.
+
+Reminder: When connecting capacitors $C_1$, $C_2$ etc in parallel, the total capacitance is $C_T = C_1 + C_2 + \cdots$, whereas when connecting them in series, the overall capacitance is given by: $\frac{1}{C_T} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots$.
+
+# --hints--
+
+`capacitanceValues()` should return `3857447`.
+
+```js
+assert.strictEqual(capacitanceValues(), 3857447);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function capacitanceValues() {
+
+ return true;
+}
+
+capacitanceValues();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-156-counting-digits.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-156-counting-digits.md
new file mode 100644
index 00000000000..fb820e64aa0
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-156-counting-digits.md
@@ -0,0 +1,68 @@
+---
+id: 5900f4091000cf542c50ff1b
+title: 'Problem 156: Counting Digits'
+challengeType: 1
+forumTopicId: 301787
+dashedName: problem-156-counting-digits
+---
+
+# --description--
+
+Starting from zero the natural numbers are written down in base 10 like this:
+
+0 1 2 3 4 5 6 7 8 9 10 11 12....
+
+Consider the digit $d = 1$. After we write down each number n, we will update the number of ones that have occurred and call this number $f(n, 1)$. The first values for $f(n, 1)$, then, are as follows:
+
+| $n$ | $f(n, 1)$ |
+| --- | --------- |
+| 0 | 0 |
+| 1 | 1 |
+| 2 | 1 |
+| 3 | 1 |
+| 4 | 1 |
+| 5 | 1 |
+| 6 | 1 |
+| 7 | 1 |
+| 8 | 1 |
+| 9 | 1 |
+| 10 | 2 |
+| 11 | 4 |
+| 12 | 5 |
+
+Note that $f(n, 1)$ never equals 3.
+
+So the first two solutions of the equation $f(n, 1) = n$ are $n = 0$ and $n = 1$. The next solution is $n = 199981$. In the same manner the function $f(n, d)$ gives the total number of digits d that have been written down after the number $n$ has been written.
+
+In fact, for every digit $d ≠ 0$, 0 is the first solution of the equation $f(n, d) = n$. Let $s(d)$ be the sum of all the solutions for which $f(n, d) = n$.
+
+You are given that $s(1) = 22786974071$. Find $\sum{s(d)}$ for $1 ≤ d ≤ 9$.
+
+Note: if, for some $n$, $f(n, d) = n$ for more than one value of $d$ this value of $n$ is counted again for every value of $d$ for which $f(n, d) = n$.
+
+# --hints--
+
+`countingDigits()` should return `21295121502550`.
+
+```js
+assert.strictEqual(countingDigits(), 21295121502550);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function countingDigits() {
+
+ return true;
+}
+
+countingDigits();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-157-solving-the-diophantine-equation.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-157-solving-the-diophantine-equation.md
new file mode 100644
index 00000000000..aa5e8185547
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-157-solving-the-diophantine-equation.md
@@ -0,0 +1,47 @@
+---
+id: 5900f4091000cf542c50ff1c
+title: 'Problem 157: Solving the diophantine equation'
+challengeType: 1
+forumTopicId: 301788
+dashedName: problem-157-solving-the-diophantine-equation
+---
+
+# --description--
+
+Consider the diophantine equation $\frac{1}{a} + \frac{1}{b} = \frac{p}{{10}^n}$ with $a$, $b$, $p$, $n$ positive integers and $a ≤ b$.
+
+For $n = 1$ this equation has 20 solutions that are listed below:
+
+$$\begin{array}{lllll} \frac{1}{1} + \frac{1}{1} = \frac{20}{10} & \frac{1}{1} + \frac{1}{2} = \frac{15}{10} & \frac{1}{1} + \frac{1}{5} = \frac{12}{10} & \frac{1}{1} + \frac{1}{10} = \frac{11}{10} & \frac{1}{2} + \frac{1}{2} = \frac{10}{10} \\\\
+ \frac{1}{2} + \frac{1}{5} = \frac{7}{10} & \frac{1}{2} + \frac{1}{10} = \frac{6}{10} & \frac{1}{3} + \frac{1}{6} = \frac{5}{10} & \frac{1}{3} + \frac{1}{15} = \frac{4}{10} & \frac{1}{4} + \frac{1}{4} = \frac{5}{10} \\\\
+ \frac{1}{4} + \frac{1}{4} = \frac{5}{10} & \frac{1}{5} + \frac{1}{5} = \frac{4}{10} & \frac{1}{5} + \frac{1}{10} = \frac{3}{10} & \frac{1}{6} + \frac{1}{30} = \frac{2}{10} & \frac{1}{10} + \frac{1}{10} = \frac{2}{10} \\\\
+ \frac{1}{11} + \frac{1}{110} = \frac{1}{10} & \frac{1}{12} + \frac{1}{60} = \frac{1}{10} & \frac{1}{14} + \frac{1}{35} = \frac{1}{10} & \frac{1}{15} + \frac{1}{30} = \frac{1}{10} & \frac{1}{20} + \frac{1}{20} = \frac{1}{10} \end{array}$$
+
+How many solutions has this equation for $1 ≤ n ≤ 9$?
+
+# --hints--
+
+`diophantineEquation()` should return `53490`.
+
+```js
+assert.strictEqual(diophantineEquation(), 53490);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function diophantineEquation() {
+
+ return true;
+}
+
+diophantineEquation();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-158-exploring-strings-for-which-only-one-character-comes-lexicographically-after-its-neighbour-to-the-left.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-158-exploring-strings-for-which-only-one-character-comes-lexicographically-after-its-neighbour-to-the-left.md
new file mode 100644
index 00000000000..845e2be3303
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-158-exploring-strings-for-which-only-one-character-comes-lexicographically-after-its-neighbour-to-the-left.md
@@ -0,0 +1,54 @@
+---
+id: 5900f40a1000cf542c50ff1d
+title: >-
+ Problem 158: Exploring strings for which only one character comes lexicographically after its neighbour to the left
+challengeType: 1
+forumTopicId: 301789
+dashedName: >-
+ problem-158-exploring-strings-for-which-only-one-character-comes-lexicographically-after-its-neighbour-to-the-left
+---
+
+# --description--
+
+Taking three different letters from the 26 letters of the alphabet, character strings of length three can be formed.
+
+Examples are 'abc', 'hat' and 'zyx'.
+
+When we study these three examples we see that for 'abc' two characters come lexicographically after its neighbour to the left.
+
+For 'hat' there is exactly one character that comes lexicographically after its neighbour to the left. For 'zyx' there are zero characters that come lexicographically after its neighbour to the left.
+
+In all there are 10400 strings of length 3 for which exactly one character comes lexicographically after its neighbour to the left.
+
+We now consider strings of $n ≤ 26$ different characters from the alphabet.
+
+For every $n$, $p(n)$ is the number of strings of length $n$ for which exactly one character comes lexicographically after its neighbour to the left.
+
+What is the maximum value of $p(n)$?
+
+# --hints--
+
+`lexicographicNeighbours()` should return `409511334375`.
+
+```js
+assert.strictEqual(lexicographicNeighbours(), 409511334375);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function lexicographicNeighbours() {
+
+ return true;
+}
+
+lexicographicNeighbours();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-159-digital-root-sums-of-factorisations.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-159-digital-root-sums-of-factorisations.md
new file mode 100644
index 00000000000..07a2e4945a4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-159-digital-root-sums-of-factorisations.md
@@ -0,0 +1,63 @@
+---
+id: 5900f40c1000cf542c50ff1e
+title: 'Problem 159: Digital root sums of factorisations'
+challengeType: 1
+forumTopicId: 301790
+dashedName: problem-159-digital-root-sums-of-factorisations
+---
+
+# --description--
+
+A composite number can be factored many different ways.
+
+For instance, not including multiplication by one, 24 can be factored in 7 distinct ways:
+
+$$\begin{align} & 24 = 2 \times 2 \times 2 \times 3\\\\
+ & 24 = 2 \times 3 \times 4 \\\\ & 24 = 2 \times 2 \times 6 \\\\
+ & 24 = 4 \times 6 \\\\ & 24 = 3 \times 8 \\\\
+ & 24 = 2 \times 12 \\\\ & 24 = 24 \end{align}$$
+
+Recall that the digital root of a number, in base 10, is found by adding together the digits of that number, and repeating that process until a number arrives at less than 10. Thus the digital root of 467 is 8.
+
+We shall call a Digital Root Sum (DRS) the sum of the digital roots of the individual factors of our number. The chart below demonstrates all of the DRS values for 24.
+
+| Factorisation | Digital Root Sum |
+| ------------- | ---------------- |
+| 2x2x2x3 | 9 |
+| 2x3x4 | 9 |
+| 2x2x6 | 10 |
+| 4x6 | 10 |
+| 3x8 | 11 |
+| 2x12 | 5 |
+| 24 | 6 |
+
+The maximum Digital Root Sum of 24 is 11. The function $mdrs(n)$ gives the maximum Digital Root Sum of $n$. So $mdrs(24) = 11$.
+
+Find $\sum{mdrs(n)}$ for $1 < n < 1,000,000$.
+
+# --hints--
+
+`euler159()` should return `14489159`.
+
+```js
+assert.strictEqual(euler159(), 14489159);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function euler159() {
+
+ return true;
+}
+
+euler159();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-160-factorial-trailing-digits.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-160-factorial-trailing-digits.md
new file mode 100644
index 00000000000..ceec9db70d3
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-160-factorial-trailing-digits.md
@@ -0,0 +1,45 @@
+---
+id: 5900f40d1000cf542c50ff1f
+title: 'Problem 160: Factorial trailing digits'
+challengeType: 1
+forumTopicId: 301794
+dashedName: problem-160-factorial-trailing-digits
+---
+
+# --description--
+
+For any $N$, let $f(N)$ be the last five digits before the trailing zeroes in $N!$.
+
+For example,
+
+$$\begin{align} & 9! = 362880 \\; \text{so} \\; f(9) = 36288 \\\\
+ & 10! = 3628800 \\; \text{so} \\; f(10) = 36288 \\\\ & 20! = 2432902008176640000 \\; \text{so} \\; f(20) = 17664 \end{align}$$
+
+Find $f(1,000,000,000,000)$
+
+# --hints--
+
+`factorialTrailingDigits()` should return `16576`.
+
+```js
+assert.strictEqual(factorialTrailingDigits(), 16576);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function factorialTrailingDigits() {
+
+ return true;
+}
+
+factorialTrailingDigits();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-161-triominoes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-161-triominoes.md
new file mode 100644
index 00000000000..8e0a070c788
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-161-triominoes.md
@@ -0,0 +1,52 @@
+---
+id: 5900f40d1000cf542c50ff20
+title: 'Problem 161: Triominoes'
+challengeType: 1
+forumTopicId: 301795
+dashedName: problem-161-triominoes
+---
+
+# --description--
+
+A triomino is a shape consisting of three squares joined via the edges.
+
+There are two basic forms:
+
+
+
+If all possible orientations are taken into account there are six:
+
+
+
+Any n by m grid for which nxm is divisible by 3 can be tiled with triominoes. If we consider tilings that can be obtained by reflection or rotation from another tiling as different there are 41 ways a 2 by 9 grid can be tiled with triominoes:
+
+
+
+In how many ways can a 9 by 12 grid be tiled in this way by triominoes?
+
+# --hints--
+
+`triominoes()` should return `20574308184277972`.
+
+```js
+assert.strictEqual(triominoes(), 20574308184277972);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function triominoes() {
+
+ return true;
+}
+
+triominoes();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-162-hexadecimal-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-162-hexadecimal-numbers.md
new file mode 100644
index 00000000000..9ad940349fe
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-162-hexadecimal-numbers.md
@@ -0,0 +1,58 @@
+---
+id: 5900f40e1000cf542c50ff21
+title: 'Problem 162: Hexadecimal numbers'
+challengeType: 1
+forumTopicId: 301796
+dashedName: problem-162-hexadecimal-numbers
+---
+
+# --description--
+
+In the hexadecimal number system numbers are represented using 16 different digits:
+
+$$0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F$$
+
+The hexadecimal number AF when written in the decimal number system equals $10 \times 16 + 15 = 175$.
+
+In the 3-digit hexadecimal numbers 10A, 1A0, A10, and A01 the digits 0,1 and A are all present.
+
+Like numbers written in base ten we write hexadecimal numbers without leading zeroes.
+
+How many hexadecimal numbers containing at most sixteen hexadecimal digits exist with all of the digits 0,1, and A present at least once?
+
+Give your answer with hexadecimal number as a string.
+
+**Note:** (A,B,C,D,E and F in upper case, without any leading or trailing code that marks the number as hexadecimal and without leading zeroes , e.g. 1A3F and not: 1a3f and not 0x1a3f and not $1A3F and not #1A3F and not 0000001A3F)
+
+# --hints--
+
+`hexadecimalNumbers()` should return a string.
+
+```js
+assert(typeof hexadecimalNumbers() === 'string');
+```
+
+`hexadecimalNumbers()` should return the string `3D58725572C62302`.
+
+```js
+assert.strictEqual(hexadecimalNumbers(), '3D58725572C62302');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function hexadecimalNumbers() {
+
+ return true;
+}
+
+hexadecimalNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-163-cross-hatched-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-163-cross-hatched-triangles.md
new file mode 100644
index 00000000000..e5fa50fb8e9
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-163-cross-hatched-triangles.md
@@ -0,0 +1,51 @@
+---
+id: 5900f40f1000cf542c50ff22
+title: 'Problem 163: Cross-hatched triangles'
+challengeType: 1
+forumTopicId: 301797
+dashedName: problem-163-cross-hatched-triangles
+---
+
+# --description--
+
+Consider an equilateral triangle in which straight lines are drawn from each vertex to the middle of the opposite side, such as in the size 1 triangle in the sketch below.
+
+
+
+Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle.
+
+It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size $n$ triangle would thus contain $n^2$ size 1 triangle building blocks.
+
+If we denote $T(n)$ as the number of triangles present in a triangle of size $n$, then
+
+$$\begin{align} & T(1) = 16 \\\\
+ & T(2) = 104 \end{align}$$
+
+Find $T(36)$.
+
+# --hints--
+
+`crossHatchedTriangles()` should return `343047`.
+
+```js
+assert.strictEqual(crossHatchedTriangles(), 343047);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function crossHatchedTriangles() {
+
+ return true;
+}
+
+crossHatchedTriangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
new file mode 100644
index 00000000000..83215f99ba4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
@@ -0,0 +1,40 @@
+---
+id: 5900f4111000cf542c50ff23
+title: >-
+ Problem 164: Numbers for which no three consecutive digits have a sum greater than a given value
+challengeType: 1
+forumTopicId: 301798
+dashedName: >-
+ problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value
+---
+
+# --description--
+
+How many 20 digit numbers $n$ (without any leading zero) exist such that no three consecutive digits of $n$ have a sum greater than 9?
+
+# --hints--
+
+`consecutiveDigitsSum()` should return `378158756814587`.
+
+```js
+assert.strictEqual(consecutiveDigitsSum(), 378158756814587);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function consecutiveDigitsSum() {
+
+ return true;
+}
+
+consecutiveDigitsSum();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-165-intersections.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-165-intersections.md
new file mode 100644
index 00000000000..04fef3d3e53
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-165-intersections.md
@@ -0,0 +1,64 @@
+---
+id: 5900f4111000cf542c50ff24
+title: 'Problem 165: Intersections'
+challengeType: 1
+forumTopicId: 301799
+dashedName: problem-165-intersections
+---
+
+# --description--
+
+A segment is uniquely defined by its two endpoints. By considering two line segments in plane geometry there are three possibilities: the segments have zero points, one point, or infinitely many points in common.
+
+Moreover when two segments have exactly one point in common it might be the case that that common point is an endpoint of either one of the segments or of both. If a common point of two segments is not an endpoint of either of the segments it is an interior point of both segments.
+
+We will call a common point $T$ of two segments $L_1$ and $L_2$ a true intersection point of $L_1$ and $L_2$ if $T$ is the only common point of $L_1$ and $L_2$ and $T$ is an interior point of both segments.
+
+Consider the three segments $L_1$, $L_2$, and $L_3$:
+
+$$\begin{align} & L_1: (27, 44) \\;\text{to}\\; (12, 32) \\\\
+ & L_2: (46, 53) \\;\text{to}\\; (17, 62) \\\\ & L_3: (46, 70) \\;\text{to}\\; (22, 40) \\\\
+\end{align}$$
+
+It can be verified that line segments $L_2$ and $L_3$ have a true intersection point. We note that as the one of the end points of $L_3$: (22, 40) lies on $L_1$ this is not considered to be a true point of intersection. $L_1$ and $L_2$ have no common point. So among the three line segments, we find one true intersection point.
+
+Now let us do the same for 5000 line segments. To this end, we generate 20000 numbers using the so-called "Blum Blum Shub" pseudo-random number generator.
+
+$$\begin{align} & s_0 = 290797 \\\\
+ & s_{n + 1} = s_n × s_n (\text{modulo}\\; 50515093) \\\\ & t_n = s_n (\text{modulo}\\; 500) \\\\
+\end{align}$$
+
+To create each line segment, we use four consecutive numbers $t_n$. That is, the first line segment is given by:
+
+($_t$1, $t_2$) to ($t_3$, $t_4$)
+
+The first four numbers computed according to the above generator should be: 27, 144, 12 and 232. The first segment would thus be (27, 144) to (12, 232).
+
+How many distinct true intersection points are found among the 5000 line segments?
+
+# --hints--
+
+`distinctIntersections()` should return `2868868`.
+
+```js
+assert.strictEqual(distinctIntersections(), 2868868);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function distinctIntersections() {
+
+ return true;
+}
+
+distinctIntersections();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-166-criss-cross.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-166-criss-cross.md
new file mode 100644
index 00000000000..f413a225835
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-166-criss-cross.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4131000cf542c50ff25
+title: 'Problem 166: Criss Cross'
+challengeType: 1
+forumTopicId: 301800
+dashedName: problem-166-criss-cross
+---
+
+# --description--
+
+A 4x4 grid is filled with digits $d$, $0 ≤ d ≤ 9$.
+
+It can be seen that in the grid
+
+$$\begin{array}{} 6 & 3 & 3 & 0 \\\\
+ 5 & 0 & 4 & 3 \\\\ 0 & 7 & 1 & 4 \\\\
+ 1 & 2 & 4 & 5 \end{array}$$
+
+the sum of each row and each column has the value 12. Moreover the sum of each diagonal is also 12.
+
+In how many ways can you fill a 4x4 grid with the digits $d$, $0 ≤ d ≤ 9$ so that each row, each column, and both diagonals have the same sum?
+
+# --hints--
+
+`crissCross()` should return `7130034`.
+
+```js
+assert.strictEqual(crissCross(), 7130034);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function crissCross() {
+
+ return true;
+}
+
+crissCross();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-167-investigating-ulam-sequences.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-167-investigating-ulam-sequences.md
new file mode 100644
index 00000000000..37f3fd53c28
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-167-investigating-ulam-sequences.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4141000cf542c50ff26
+title: 'Problem 167: Investigating Ulam sequences'
+challengeType: 1
+forumTopicId: 301801
+dashedName: problem-167-investigating-ulam-sequences
+---
+
+# --description--
+
+For two positive integers $a$ and $b$, the Ulam sequence $U(a,b)$ is defined by ${U{(a,b)}\_1} = a$, ${U{(a,b)}\_2} = b$ and for $k > 2$, ${U{(a,b)}\_k}$ is the smallest integer greater than ${U{(a,b)}\_{(k-1)}}$ which can be written in exactly one way as the sum of two distinct previous members of $U(a,b)$.
+
+For example, the sequence $U(1,2)$ begins with
+
+$$1, 2, 3 = 1 + 2, 4 = 1 + 3, 6 = 2 + 4, 8 = 2 + 6, 11 = 3 + 8$$
+
+5 does not belong to it because $5 = 1 + 4 = 2 + 3$ has two representations as the sum of two previous members, likewise $7 = 1 + 6 = 3 + 4$.
+
+Find $\sum {U(2, 2n + 1)_k}$ for $2 ≤ n ≤ 10$, where $k = {10}^{11}$.
+
+# --hints--
+
+`ulamSequences()` should return `3916160068885`.
+
+```js
+assert.strictEqual(ulamSequences(), 3916160068885);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function ulamSequences() {
+
+ return true;
+}
+
+ulamSequences();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-168-number-rotations.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-168-number-rotations.md
new file mode 100644
index 00000000000..50802415375
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-168-number-rotations.md
@@ -0,0 +1,82 @@
+---
+id: 5900f4151000cf542c50ff27
+title: 'Problem 168: Number Rotations'
+challengeType: 1
+forumTopicId: 301802
+dashedName: problem-168-number-rotations
+---
+
+# --description--
+
+Consider the number 142857. We can right-rotate this number by moving the last digit (7) to the front of it, giving us 714285.
+
+It can be verified that $714285 = 5 × 142857$.
+
+This demonstrates an unusual property of 142857: it is a divisor of its right-rotation.
+
+For integer number of digits $a$ and $b$, find the last 5 digits of the sum of all integers $n$, $10^a < n < 10^b$, that have this property.
+
+# --hints--
+
+`numberRotations(2, 10)` should return `98311`.
+
+```js
+assert.strictEqual(numberRotations(2, 10), 98311);
+```
+
+`numberRotations(2, 100)` should return `59206`.
+
+```js
+assert.strictEqual(numberRotations(2, 100), 59206);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function numberRotations(a, b) {
+
+ return 0;
+}
+
+numberRotations();
+```
+
+# --solutions--
+
+```js
+function numberRotations(minDigits, maxDigits) {
+ const DIGITS_TO_KEEP = 100000n;
+ const powersOfTen = Array(maxDigits).fill(0);
+ powersOfTen[0] = 1n;
+ for (let i = 1; i < maxDigits; i++) {
+ powersOfTen[i] = powersOfTen[i - 1] * 10n;
+ }
+
+ // We want numbers of the form xd * m = dx
+ // Or more precisely:
+ // (x * 10 + d) * m = d*10^(n-1) + x
+ // Solving for x:
+ // x = d (10^(n-1) - m) / (10 * m - 1)
+ let total = 0n;
+ for (let numDigits = minDigits; numDigits <= maxDigits; numDigits++) {
+ // Check all multiplier - digit pairs to see if a candidate can be built
+ // with the correct number of digits
+ for (let multiplier = 1n; multiplier < 10n; multiplier++) {
+ for (let lastDigit = 1n; lastDigit < 10n; lastDigit++) {
+ const numerator = lastDigit * (powersOfTen[numDigits - 1] - multiplier);
+ const denominator = (powersOfTen[1] * multiplier - 1n);
+ if (numerator % denominator === 0n) {
+ const candidate = (numerator / denominator) * 10n + lastDigit;
+ if (candidate.toString().length === numDigits) {
+ total = (total + candidate) % DIGITS_TO_KEEP;
+ }
+ }
+ }
+ }
+ }
+
+ return parseInt(total);
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
new file mode 100644
index 00000000000..52005157a98
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4151000cf542c50ff28
+title: >-
+ Problem 169: Exploring the number of different ways a number can be expressed as a sum of powers of 2
+challengeType: 1
+forumTopicId: 301803
+dashedName: >-
+ problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2
+---
+
+# --description--
+
+Define $f(0)=1$ and $f(n)$ to be the number of different ways $n$ can be expressed as a sum of integer powers of 2 using each power no more than twice.
+
+For example, $f(10)=5$ since there are five different ways to express 10:
+
+$$\begin{align} & 1 + 1 + 8 \\\\
+ & 1 + 1 + 4 + 4 \\\\ & 1 + 1 + 2 + 2 + 4 \\\\
+ & 2 + 4 + 4 \\\\ & 2 + 8 \end{align}$$
+
+What is $f({10}^{25})$?
+
+# --hints--
+
+`numberOfWaysToExpress()` should return `178653872807`.
+
+```js
+assert.strictEqual(numberOfWaysToExpress(), 178653872807);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function numberOfWaysToExpress() {
+
+ return true;
+}
+
+numberOfWaysToExpress();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
new file mode 100644
index 00000000000..b6886e18764
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
@@ -0,0 +1,49 @@
+---
+id: 5900f4161000cf542c50ff29
+title: >-
+ Problem 170: Find the largest 0 to 9 pandigital that can be formed by concatenating products
+challengeType: 1
+forumTopicId: 301805
+dashedName: >-
+ problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products
+---
+
+# --description--
+
+Take the number 6 and multiply it by each of 1273 and 9854:
+
+$$\begin{align} & 6 × 1273 = 7638 \\\\
+ & 6 × 9854 = 59124 \\\\ \end{align}$$
+
+By concatenating these products we get the 1 to 9 pandigital 763859124. We will call 763859124 the "concatenated product of 6 and (1273, 9854)". Notice too, that the concatenation of the input numbers, 612739854, is also 1 to 9 pandigital.
+
+The same can be done for 0 to 9 pandigital numbers.
+
+What is the largest 0 to 9 pandigital 10-digit concatenated product of an integer with two or more other integers, such that the concatenation of the input numbers is also a 0 to 9 pandigital 10-digit number?
+
+# --hints--
+
+`largestPandigital()` should return `9857164023`.
+
+```js
+assert.strictEqual(largestPandigital(), 9857164023);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function largestPandigital() {
+
+ return true;
+}
+
+largestPandigital();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
new file mode 100644
index 00000000000..60133bf2e51
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4181000cf542c50ff2a
+title: >-
+ Problem 171: Finding numbers for which the sum of the squares of the digits is a square
+challengeType: 1
+forumTopicId: 301806
+dashedName: >-
+ problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square
+---
+
+# --description--
+
+For a positive integer $n$, let $f(n)$ be the sum of the squares of the digits (in base 10) of $n$, e.g.
+
+$$\begin{align} & f(3) = 3^2 = 9 \\\\
+ & f(25) = 2^2 + 5^2 = 4 + 25 = 29 \\\\ & f(442) = 4^2 + 4^2 + 2^2 = 16 + 16 + 4 = 36 \\\\
+\end{align}$$
+
+Find the last nine digits of the sum of all $n$, $0 < n < {10}^{20}$, such that $f(n)$ is a perfect square.
+
+# --hints--
+
+`lastDigitsSumOfPerfectSquare()` should return `142989277`.
+
+```js
+assert.strictEqual(lastDigitsSumOfPerfectSquare(), 142989277);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function lastDigitsSumOfPerfectSquare() {
+
+ return true;
+}
+
+lastDigitsSumOfPerfectSquare();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-172-investigating-numbers-with-few-repeated-digits.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-172-investigating-numbers-with-few-repeated-digits.md
new file mode 100644
index 00000000000..cfc75b9ff19
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-172-investigating-numbers-with-few-repeated-digits.md
@@ -0,0 +1,38 @@
+---
+id: 5900f4181000cf542c50ff2b
+title: 'Problem 172: Investigating numbers with few repeated digits'
+challengeType: 1
+forumTopicId: 301807
+dashedName: problem-172-investigating-numbers-with-few-repeated-digits
+---
+
+# --description--
+
+How many 18-digit numbers $n$ (without leading zeros) are there such that no digit occurs more than three times in $n$?
+
+# --hints--
+
+`numbersWithRepeatedDigits()` should return `227485267000992000`.
+
+```js
+assert.strictEqual(numbersWithRepeatedDigits(), 227485267000992000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function numbersWithRepeatedDigits() {
+
+ return true;
+}
+
+numbersWithRepeatedDigits();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
new file mode 100644
index 00000000000..0488d662943
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
@@ -0,0 +1,44 @@
+---
+id: 5900f41a1000cf542c50ff2c
+title: >-
+ Problem 173: Using up to one million tiles how many different "hollow" square laminae can be formed?
+challengeType: 1
+forumTopicId: 301808
+dashedName: >-
+ problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed
+---
+
+# --description--
+
+We shall define a square lamina to be a square outline with a square "hole" so that the shape possesses vertical and horizontal symmetry. For example, using exactly thirty-two square tiles we can form two different square laminae:
+
+
+
+With one-hundred tiles, and not necessarily using all of the tiles at one time, it is possible to form forty-one different square laminae. Using up to one million tiles how many different square laminae can be formed?
+
+# --hints--
+
+`differentHollowSquareLaminae()` should return `1572729`.
+
+```js
+assert.strictEqual(differentHollowSquareLaminae(), 1572729);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function differentHollowSquareLaminae() {
+
+ return true;
+}
+
+differentHollowSquareLaminae();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
new file mode 100644
index 00000000000..48843b6b0a9
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
@@ -0,0 +1,50 @@
+---
+id: 5900f41a1000cf542c50ff2d
+title: >-
+ Problem 174: Counting the number of "hollow" square laminae that can form one, two, three, ... distinct arrangements
+challengeType: 1
+forumTopicId: 301809
+dashedName: >-
+ problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-----distinct-arrangements
+---
+
+# --description--
+
+We shall define a square lamina to be a square outline with a square "hole" so that the shape possesses vertical and horizontal symmetry.
+
+Given eight tiles it is possible to form a lamina in only one way: 3x3 square with a 1x1 hole in the middle. However, using thirty-two tiles it is possible to form two distinct laminae.
+
+
+
+If $t$ represents the number of tiles used, we shall say that $t = 8$ is type $L(1)$ and $t = 32$ is type $L(2)$.
+
+Let $N(n)$ be the number of $t ≤ 1000000$ such that $t$ is type $L(n)$; for example, $N(15) = 832$.
+
+What is $\sum N(n)$ for $1 ≤ n ≤ 10$?
+
+# --hints--
+
+`hollowSquareLaminaeDistinctArrangements()` should return `209566`.
+
+```js
+assert.strictEqual(hollowSquareLaminaeDistinctArrangements(), 209566);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function hollowSquareLaminaeDistinctArrangements() {
+
+ return true;
+}
+
+hollowSquareLaminaeDistinctArrangements();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
new file mode 100644
index 00000000000..b3419c34823
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
@@ -0,0 +1,62 @@
+---
+id: 5900f41c1000cf542c50ff2e
+title: >-
+ Problem 175: Fractions involving the number of different ways a number can be expressed as a sum of powers of 2
+challengeType: 1
+forumTopicId: 301810
+dashedName: >-
+ problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2
+---
+
+# --description--
+
+Define $f(0) = 1$ and $f(n)$ to be the number of ways to write $n$ as a sum of powers of 2 where no power occurs more than twice.
+
+For example, $f(10) = 5$ since there are five different ways to express 10:
+
+$$10 = 8 + 2 = 8 + 1 + 1 = 4 + 4 + 2 = 4 + 2 + 2 + 1 + 1 = 4 + 4 + 1 + 1$$
+
+It can be shown that for every fraction $\frac{p}{q}\\; (p>0, q>0)$ there exists at least one integer $n$ such that $\frac{f(n)}{f(n - 1)} = \frac{p}{q}$.
+
+For instance, the smallest $n$ for which $\frac{f(n)}{f(n - 1)} = \frac{13}{17}$ is 241. The binary expansion of 241 is 11110001.
+
+Reading this binary number from the most significant bit to the least significant bit there are 4 one's, 3 zeroes and 1 one. We shall call the string 4,3,1 the Shortened Binary Expansion of 241.
+
+Find the Shortened Binary Expansion of the smallest $n$ for which
+
+$$\frac{f(n)}{f(n - 1)} = \frac{123456789}{987654321}$$
+
+Give your answer as a string with comma separated integers, without any whitespaces.
+
+# --hints--
+
+`shortenedBinaryExpansionOfNumber()` should return a string.
+
+```js
+assert(typeof shortenedBinaryExpansionOfNumber() === 'string');
+```
+
+`shortenedBinaryExpansionOfNumber()` should return the string `1,13717420,8`.
+
+```js
+assert.strictEqual(shortenedBinaryExpansionOfNumber(), '1,13717420,8');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function shortenedBinaryExpansionOfNumber() {
+
+ return true;
+}
+
+shortenedBinaryExpansionOfNumber();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-176-right-angled-triangles-that-share-a-cathetus.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-176-right-angled-triangles-that-share-a-cathetus.md
new file mode 100644
index 00000000000..01056496296
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-176-right-angled-triangles-that-share-a-cathetus.md
@@ -0,0 +1,40 @@
+---
+id: 5900f41c1000cf542c50ff2f
+title: 'Problem 176: Right-angled triangles that share a cathetus'
+challengeType: 1
+forumTopicId: 301811
+dashedName: problem-176-right-angled-triangles-that-share-a-cathetus
+---
+
+# --description--
+
+The four right-angled triangles with sides (9,12,15), (12,16,20), (5,12,13) and (12,35,37) all have one of the shorter sides (catheti) equal to 12. It can be shown that no other integer sided right-angled triangle exists with one of the catheti equal to 12.
+
+Find the smallest integer that can be the length of a cathetus of exactly 47547 different integer sided right-angled triangles.
+
+# --hints--
+
+`trianglesSharingCathetus()` should return `96818198400000`.
+
+```js
+assert.strictEqual(trianglesSharingCathetus(), 96818198400000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function trianglesSharingCathetus() {
+
+ return true;
+}
+
+trianglesSharingCathetus();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-177-integer-angled-quadrilaterals.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-177-integer-angled-quadrilaterals.md
new file mode 100644
index 00000000000..c6f7b8ee5c4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-177-integer-angled-quadrilaterals.md
@@ -0,0 +1,48 @@
+---
+id: 5900f41e1000cf542c50ff30
+title: 'Problem 177: Integer angled Quadrilaterals'
+challengeType: 1
+forumTopicId: 301812
+dashedName: problem-177-integer-angled-quadrilaterals
+---
+
+# --description--
+
+Let ABCD be a convex quadrilateral, with diagonals AC and BD. At each vertex the diagonal makes an angle with each of the two sides, creating eight corner angles.
+
+
+
+For example, at vertex A, the two angles are CAD, CAB.
+
+We call such a quadrilateral for which all eight corner angles have integer values when measured in degrees an "integer angled quadrilateral". An example of an integer angled quadrilateral is a square, where all eight corner angles are 45°. Another example is given by DAC = 20°, BAC = 60°, ABD = 50°, CBD = 30°, BCA = 40°, DCA = 30°, CDB = 80°, ADB = 50°.
+
+What is the total number of non-similar integer angled quadrilaterals?
+
+**Note:** In your calculations you may assume that a calculated angle is integral if it is within a tolerance of ${10}^{-9}$ of an integer value.
+
+# --hints--
+
+`integerAngledQuadrilaterals()` should return `129325`.
+
+```js
+assert.strictEqual(integerAngledQuadrilaterals(), 129325);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function integerAngledQuadrilaterals() {
+
+ return true;
+}
+
+integerAngledQuadrilaterals();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-178-step-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-178-step-numbers.md
new file mode 100644
index 00000000000..22f44139de6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-178-step-numbers.md
@@ -0,0 +1,46 @@
+---
+id: 5900f41e1000cf542c50ff31
+title: 'Problem 178: Step Numbers'
+challengeType: 1
+forumTopicId: 301813
+dashedName: problem-178-step-numbers
+---
+
+# --description--
+
+Consider the number 45656.
+
+It can be seen that each pair of consecutive digits of 45656 has a difference of one.
+
+A number for which every pair of consecutive digits has a difference of one is called a step number.
+
+A pandigital number contains every decimal digit from 0 to 9 at least once.
+
+How many pandigital step numbers less than ${10}^{40}$ are there?
+
+# --hints--
+
+`stepNumbers()` should return `126461847755`.
+
+```js
+assert.strictEqual(stepNumbers(), 126461847755);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function stepNumbers() {
+
+ return true;
+}
+
+stepNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-179-consecutive-positive-divisors.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-179-consecutive-positive-divisors.md
new file mode 100644
index 00000000000..a159a7af8f6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-179-consecutive-positive-divisors.md
@@ -0,0 +1,38 @@
+---
+id: 5900f41f1000cf542c50ff32
+title: 'Problem 179: Consecutive positive divisors'
+challengeType: 1
+forumTopicId: 301814
+dashedName: problem-179-consecutive-positive-divisors
+---
+
+# --description--
+
+Find the number of integers $1 < n < {10}^7$, for which $n$ and $n + 1$ have the same number of positive divisors. For example, 14 has the positive divisors 1, 2, 7, 14 while 15 has 1, 3, 5, 15.
+
+# --hints--
+
+`consecutivePositiveDivisors()` should return `986262`.
+
+```js
+assert.strictEqual(consecutivePositiveDivisors(), 986262);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function consecutivePositiveDivisors() {
+
+ return true;
+}
+
+consecutivePositiveDivisors();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-180-rational-zeros-of-a-function-of-three-variables.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-180-rational-zeros-of-a-function-of-three-variables.md
new file mode 100644
index 00000000000..9eed96d38b2
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-180-rational-zeros-of-a-function-of-three-variables.md
@@ -0,0 +1,53 @@
+---
+id: 5900f4201000cf542c50ff33
+title: 'Problem 180: Rational zeros of a function of three variables'
+challengeType: 1
+forumTopicId: 301816
+dashedName: problem-180-rational-zeros-of-a-function-of-three-variables
+---
+
+# --description--
+
+For any integer $n$, consider the three functions
+
+$$\begin{align} & f_{1,n}(x,y,z) = x^{n + 1} + y^{n + 1} − z^{n + 1}\\\\
+ & f_{2,n}(x,y,z) = (xy + yz + zx) \times (x^{n - 1} + y^{n - 1} − z^{n - 1})\\\\ & f_{3,n}(x,y,z) = xyz \times (x^{n - 2} + y^{n - 2} − z^{n - 2}) \end{align}$$
+
+and their combination
+
+$$\begin{align} & f_n(x,y,z) = f_{1,n}(x,y,z) + f_{2,n}(x,y,z) − f_{3,n}(x,y,z) \end{align}$$
+
+We call $(x,y,z)$ a golden triple of order $k$ if $x$, $y$, and $z$ are all rational numbers of the form $\frac{a}{b}$ with $0 < a < b ≤ k$ and there is (at least) one integer $n$, so that $f_n(x,y,z) = 0$.
+
+Let $s(x,y,z) = x + y + z$.
+
+Let $t = \frac{u}{v}$ be the sum of all distinct $s(x,y,z)$ for all golden triples $(x,y,z)$ of order 35. All the $s(x,y,z)$ and $t$ must be in reduced form.
+
+Find $u + v$.
+
+# --hints--
+
+`rationalZeros()` should return `285196020571078980`.
+
+```js
+assert.strictEqual(rationalZeros(), 285196020571078980);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function rationalZeros() {
+
+ return true;
+}
+
+rationalZeros();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-181-investigating-in-how-many-ways-objects-of-two-different-colours-can-be-grouped.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-181-investigating-in-how-many-ways-objects-of-two-different-colours-can-be-grouped.md
new file mode 100644
index 00000000000..f98d3a71b9e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-181-investigating-in-how-many-ways-objects-of-two-different-colours-can-be-grouped.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4231000cf542c50ff34
+title: >-
+ Problem 181: Investigating in how many ways objects of two different colours can be grouped
+challengeType: 1
+forumTopicId: 301817
+dashedName: >-
+ problem-181-investigating-in-how-many-ways-objects-of-two-different-colours-can-be-grouped
+---
+
+# --description--
+
+Having three black objects $B$ and one white object $W$ they can be grouped in 7 ways like this:
+
+$$(BBBW)\\;(B,BBW)\\;(B,B,BW)\\;(B,B,B,W)\\;(B,BB,W)\\;(BBB,W)\\;(BB,BW)$$
+
+In how many ways can sixty black objects $B$ and forty white objects $W$ be thus grouped?
+
+# --hints--
+
+`colorsGrouping()` should return `83735848679360670`.
+
+```js
+assert.strictEqual(colorsGrouping(), 83735848679360670);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function colorsGrouping() {
+
+ return true;
+}
+
+colorsGrouping();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-182-rsa-encryption.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-182-rsa-encryption.md
new file mode 100644
index 00000000000..e971434b3e7
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-182-rsa-encryption.md
@@ -0,0 +1,102 @@
+---
+id: 5900f4231000cf542c50ff35
+title: 'Problem 182: RSA encryption'
+challengeType: 1
+forumTopicId: 301818
+dashedName: problem-182-rsa-encryption
+---
+
+# --description--
+
+The RSA encryption is based on the following procedure:
+
+Generate two distinct primes `p` and `q`. Compute `n=p*q` and `φ=(p-1)(q-1)`. Find an integer `e`, `1 < e < φ`, such that `gcd(e,φ) = 1`
+
+A message in this system is a number in the interval `[0,n-1]`. A text to be encrypted is then somehow converted to messages (numbers in the interval `[0,n-1]`). To encrypt the text, for each message, `m`, c=me mod n is calculated.
+
+To decrypt the text, the following procedure is needed: calculate `d` such that `ed=1 mod φ`, then for each encrypted message, `c`, calculate m=cd mod n.
+
+There exist values of `e` and `m` such that me mod n = m. We call messages `m` for which me mod n=m unconcealed messages.
+
+An issue when choosing `e` is that there should not be too many unconcealed messages. For instance, let `p=19` and `q=37`. Then `n=19*37=703` and `φ=18*36=648`. If we choose `e=181`, then, although `gcd(181,648)=1` it turns out that all possible messages m `(0≤m≤n-1)` are unconcealed when calculating me mod n. For any valid choice of `e` there exist some unconcealed messages. It's important that the number of unconcealed messages is at a minimum.
+
+For any given `p` and `q`, find the sum of all values of `e`, `1 < e < φ(p,q)` and `gcd(e,φ)=1`, so that the number of unconcealed messages for this value of `e` is at a minimum.
+
+# --hints--
+
+`RSAEncryption` should be a function.
+
+```js
+assert(typeof RSAEncryption === 'function')
+```
+
+`RSAEncryption` should return a number.
+
+```js
+assert.strictEqual(typeof RSAEncryption(19, 37), 'number');
+```
+
+`RSAEncryption(19, 37)` should return `17766`.
+
+```js
+assert.strictEqual(RSAEncryption(19, 37), 17766);
+```
+
+`RSAEncryption(283, 409)` should return `466196580`.
+
+```js
+assert.strictEqual(RSAEncryption(283, 409), 466196580);
+```
+
+`RSAEncryption(1009, 3643)` should return `399788195976`.
+
+```js
+assert.strictEqual(RSAEncryption(19, 37), 17766);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function RSAEncryption(p, q) {
+
+ return true;
+}
+
+RSAEncryption(19, 37);
+```
+
+# --solutions--
+
+```js
+function gcd(a, b) {
+ if (b)
+ return gcd(b, a % b);
+ else
+ return a;
+}
+
+function RSAEncryption(p, q) {
+ let phi = (p - 1) * (q - 1);
+
+ let best = Number.MAX_SAFE_INTEGER;
+ let sum = 0;
+
+ for (let e = 0; e < phi; ++e) {
+ if (!(gcd(e, phi) == 1))
+ continue;
+
+ let msg = (gcd(p - 1, e - 1) + 1) * (gcd(q - 1, e - 1) + 1);
+
+ if (best == msg) {
+ sum += e;
+ } else if (best > msg) {
+ best = msg;
+ sum = e;
+ }
+ }
+
+ return sum;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-183-maximum-product-of-parts.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-183-maximum-product-of-parts.md
new file mode 100644
index 00000000000..7586be421e3
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-183-maximum-product-of-parts.md
@@ -0,0 +1,54 @@
+---
+id: 5900f4231000cf542c50ff36
+title: 'Problem 183: Maximum product of parts'
+challengeType: 1
+forumTopicId: 301819
+dashedName: problem-183-maximum-product-of-parts
+---
+
+# --description--
+
+Let $N$ be a positive integer and let $N$ be split into $k$ equal parts, $r = \frac{N}{k}$, so that $N = r + r + \cdots + r$.
+
+Let $P$ be the product of these parts, $P = r × r × \cdots × r = r^k$.
+
+For example, if 11 is split into five equal parts, 11 = 2.2 + 2.2 + 2.2 + 2.2 + 2.2, then $P = {2.2}^5 = 51.53632$.
+
+Let $M(N) = P_{max}$ for a given value of $N$.
+
+It turns out that the maximum for $N = 11$ is found by splitting eleven into four equal parts which leads to $P_{max} = {(\frac{11}{4})}^4$; that is, $M(11) = \frac{14641}{256} = 57.19140625$, which is a terminating decimal.
+
+However, for $N = 8$ the maximum is achieved by splitting it into three equal parts, so $M(8) = \frac{512}{27}$, which is a non-terminating decimal.
+
+Let $D(N) = N$ if $M(N)$ is a non-terminating decimal and $D(N) = -N$ if $M(N)$ is a terminating decimal.
+
+For example, $\sum D(N)$ for $5 ≤ N ≤ 100$ is 2438.
+
+Find $\sum D(N)$ for $5 ≤ N ≤ 10000$.
+
+# --hints--
+
+`maximumProductOfParts()` should return `48861552`.
+
+```js
+assert.strictEqual(maximumProductOfParts(), 48861552);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function maximumProductOfParts() {
+
+ return true;
+}
+
+maximumProductOfParts();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-184-triangles-containing-the-origin.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-184-triangles-containing-the-origin.md
new file mode 100644
index 00000000000..8d3eb0bfc9d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-184-triangles-containing-the-origin.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4241000cf542c50ff37
+title: 'Problem 184: Triangles containing the origin'
+challengeType: 1
+forumTopicId: 301820
+dashedName: problem-184-triangles-containing-the-origin
+---
+
+# --description--
+
+Consider the set $I_r$ of points $(x,y)$ with integer coordinates in the interior of the circle with radius $r$, centered at the origin, i.e. $x^2 + y^2 < r^2$.
+
+For a radius of 2, $I_2$ contains the nine points (0,0), (1,0), (1,1), (0,1), (-1,1), (-1,0), (-1,-1), (0,-1) and (1,-1). There are eight triangles having all three vertices in $I_2$ which contain the origin in the interior. Two of them are shown below, the others are obtained from these by rotation.
+
+
+
+For a radius of 3, there are 360 triangles containing the origin in the interior and having all vertices in $I_3$ and for $I_5$ the number is 10600.
+
+How many triangles are there containing the origin in the interior and having all three vertices in $I_{105}$?
+
+# --hints--
+
+`trianglesContainingOrigin()` should return `1725323624056`.
+
+```js
+assert.strictEqual(trianglesContainingOrigin(), 1725323624056);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function trianglesContainingOrigin() {
+
+ return true;
+}
+
+trianglesContainingOrigin();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-185-number-mind.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-185-number-mind.md
new file mode 100644
index 00000000000..820f0832166
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-185-number-mind.md
@@ -0,0 +1,66 @@
+---
+id: 5900f4251000cf542c50ff38
+title: 'Problem 185: Number Mind'
+challengeType: 1
+forumTopicId: 301821
+dashedName: problem-185-number-mind
+---
+
+# --description--
+
+The game Number Mind is a variant of the well known game Master Mind.
+
+Instead of coloured pegs, you have to guess a secret sequence of digits. After each guess you're only told in how many places you've guessed the correct digit. So, if the sequence was 1234 and you guessed 2036, you'd be told that you have one correct digit; however, you would NOT be told that you also have another digit in the wrong place.
+
+For instance, given the following guesses for a 5-digit secret sequence,
+
+$$\begin{align} & 90342 ;2\\;\text{correct}\\\\
+ & 70794 ;0\\;\text{correct}\\\\ & 39458 ;2\\;\text{correct}\\\\
+ & 34109 ;1\\;\text{correct}\\\\ & 51545 ;2\\;\text{correct}\\\\
+ & 12531 ;1\\;\text{correct} \end{align}$$
+
+The correct sequence 39542 is unique.
+
+Based on the following guesses,
+
+$$\begin{align} & 5616185650518293 ;2\\;\text{correct}\\\\
+ & 3847439647293047 ;1\\;\text{correct}\\\\ & 5855462940810587 ;3\\;\text{correct}\\\\
+ & 9742855507068353 ;3\\;\text{correct}\\\\ & 4296849643607543 ;3\\;\text{correct}\\\\
+ & 3174248439465858 ;1\\;\text{correct}\\\\ & 4513559094146117 ;2\\;\text{correct}\\\\
+ & 7890971548908067 ;3\\;\text{correct}\\\\ & 8157356344118483 ;1\\;\text{correct}\\\\
+ & 2615250744386899 ;2\\;\text{correct}\\\\ & 8690095851526254 ;3\\;\text{correct}\\\\
+ & 6375711915077050 ;1\\;\text{correct}\\\\ & 6913859173121360 ;1\\;\text{correct}\\\\
+ & 6442889055042768 ;2\\;\text{correct}\\\\ & 2321386104303845 ;0\\;\text{correct}\\\\
+ & 2326509471271448 ;2\\;\text{correct}\\\\ & 5251583379644322 ;2\\;\text{correct}\\\\
+ & 1748270476758276 ;3\\;\text{correct}\\\\ & 4895722652190306 ;1\\;\text{correct}\\\\
+ & 3041631117224635 ;3\\;\text{correct}\\\\ & 1841236454324589 ;3\\;\text{correct}\\\\
+ & 2659862637316867 ;2\\;\text{correct} \end{align}$$
+
+Find the unique 16-digit secret sequence.
+
+# --hints--
+
+`numberMind()` should return `4640261571849533`.
+
+```js
+assert.strictEqual(numberMind(), 4640261571849533);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function numberMind() {
+
+ return true;
+}
+
+numberMind();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-186-connectedness-of-a-network.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-186-connectedness-of-a-network.md
new file mode 100644
index 00000000000..8d1fed78cdf
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-186-connectedness-of-a-network.md
@@ -0,0 +1,57 @@
+---
+id: 5900f4281000cf542c50ff39
+title: 'Problem 186: Connectedness of a network'
+challengeType: 1
+forumTopicId: 301822
+dashedName: problem-186-connectedness-of-a-network
+---
+
+# --description--
+
+Here are the records from a busy telephone system with one million users:
+
+| RecNr | Caller | Called |
+| ----- | ------ | ------ |
+| 1 | 200007 | 100053 |
+| 2 | 600183 | 500439 |
+| 3 | 600863 | 701497 |
+| ... | ... | ... |
+
+The telephone number of the caller and the called number in record $n$ are $Caller(n) = S_{2n - 1}$ and $Called(n) = S_{2n}$ where ${S}_{1,2,3,\ldots}$ come from the "Lagged Fibonacci Generator":
+
+For $1 ≤ k ≤ 55$, $S_k = [100003 - 200003k + 300007{k}^3]\\;(\text{modulo}\\;1000000)$
+
+For $56 ≤ k$, $S_k = [S_{k - 24} + S_{k - 55}]\\;(\text{modulo}\\;1000000)$
+
+If $Caller(n) = Called(n)$ then the user is assumed to have misdialled and the call fails; otherwise the call is successful.
+
+From the start of the records, we say that any pair of users $X$ and $Y$ are friends if $X$ calls $Y$ or vice-versa. Similarly, $X$ is a friend of a friend of $Z$ if $X$ is a friend of $Y$ and $Y$ is a friend of $Z$; and so on for longer chains.
+
+The Prime Minister's phone number is 524287. After how many successful calls, not counting misdials, will 99% of the users (including the PM) be a friend, or a friend of a friend etc., of the Prime Minister?
+
+# --hints--
+
+`connectednessOfANetwork()` should return `2325629`.
+
+```js
+assert.strictEqual(connectednessOfANetwork(), 2325629);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function connectednessOfANetwork() {
+
+ return true;
+}
+
+connectednessOfANetwork();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-187-semiprimes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-187-semiprimes.md
new file mode 100644
index 00000000000..bcd6f324753
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-187-semiprimes.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4291000cf542c50ff3a
+title: 'Problem 187: Semiprimes'
+challengeType: 1
+forumTopicId: 301823
+dashedName: problem-187-semiprimes
+---
+
+# --description--
+
+A composite is a number containing at least two prime factors. For example, $15 = 3 × 5; 9 = 3 × 3; 12 = 2 × 2 × 3$.
+
+There are ten composites below thirty containing precisely two, not necessarily distinct, prime factors: 4, 6, 9, 10, 14, 15, 21, 22, 25, 26.
+
+How many composite integers, $n < {10}^8$, have precisely two, not necessarily distinct, prime factors?
+
+# --hints--
+
+`semiPrimes()` should return `17427258`.
+
+```js
+assert.strictEqual(euler187(), 17427258);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function semiPrimes() {
+
+ return true;
+}
+
+semiPrimes();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-188-the-hyperexponentiation-of-a-number.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-188-the-hyperexponentiation-of-a-number.md
new file mode 100644
index 00000000000..1e0ae1dc9fa
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-188-the-hyperexponentiation-of-a-number.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4291000cf542c50ff3b
+title: 'Problem 188: The hyperexponentiation of a number'
+challengeType: 1
+forumTopicId: 301824
+dashedName: problem-188-the-hyperexponentiation-of-a-number
+---
+
+# --description--
+
+The hyperexponentiation or tetration of a number $a$ by a positive integer $b$, denoted by $a↑↑b$ or ${}^ba$, is recursively defined by:
+
+$a↑↑1 = a$,
+
+$a↑↑(k+1) = a^{(a↑↑k)}$.
+
+Thus we have e.g. $3↑↑2 = 3^3 = 27$, hence $3↑↑3 = 3^{27} = 7625597484987$ and $3↑↑4$ is roughly ${10}^{3.6383346400240996 \times {10}^{12}}$. Find the last 8 digits of $1777↑↑1855$.
+
+# --hints--
+
+`hyperexponentation()` should return `95962097`.
+
+```js
+assert.strictEqual(hyperexponentation(), 95962097);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function hyperexponentation() {
+
+ return true;
+}
+
+hyperexponentation();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-189-tri-colouring-a-triangular-grid.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-189-tri-colouring-a-triangular-grid.md
new file mode 100644
index 00000000000..6ac8cedcec5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-189-tri-colouring-a-triangular-grid.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4291000cf542c50ff3c
+title: 'Problem 189: Tri-colouring a triangular grid'
+challengeType: 1
+forumTopicId: 301825
+dashedName: problem-189-tri-colouring-a-triangular-grid
+---
+
+# --description--
+
+Consider the following configuration of 64 triangles:
+
+
+
+We wish to colour the interior of each triangle with one of three colours: red, green or blue, so that no two neighbouring triangles have the same colour. Such a colouring shall be called valid. Here, two triangles are said to be neighbouring if they share an edge. Note: if they only share a vertex, then they are not neighbours.
+
+For example, here is a valid colouring of the above grid:
+
+
+
+A colouring C' which is obtained from a colouring C by rotation or reflection is considered distinct from C unless the two are identical.
+
+How many distinct valid colourings are there for the above configuration?
+
+# --hints--
+
+`triangularGridColoring()` should return `10834893628237824`.
+
+```js
+assert.strictEqual(triangularGridColoring(), 10834893628237824);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function triangularGridColoring() {
+
+ return true;
+}
+
+triangularGridColoring();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-190-maximising-a-weighted-product.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-190-maximising-a-weighted-product.md
new file mode 100644
index 00000000000..806332925e0
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-190-maximising-a-weighted-product.md
@@ -0,0 +1,42 @@
+---
+id: 5900f42b1000cf542c50ff3d
+title: 'Problem 190: Maximising a weighted product'
+challengeType: 1
+forumTopicId: 301828
+dashedName: problem-190-maximising-a-weighted-product
+---
+
+# --description--
+
+Let $S_m = (x_1, x_2, \ldots, x_m)$ be the $m$-tuple of positive real numbers with $x_1 + x_2 + \cdots + x_m = m$ for which $P_m = x_1 \times {x_2}^2 \times \cdots \times {x_m}^m$ is maximised.
+
+For example, it can be verified that $[P_{10}] = 4112$ ([ ] is the integer part function).
+
+Find $\sum {[P_m]}$ for $2 ≤ m ≤ 15$.
+
+# --hints--
+
+`maximisingWeightedProduct()` should return `371048281`.
+
+```js
+assert.strictEqual(maximisingWeightedProduct(), 371048281);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function maximisingWeightedProduct() {
+
+ return true;
+}
+
+maximisingWeightedProduct();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-191-prize-strings.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-191-prize-strings.md
new file mode 100644
index 00000000000..8e4e35e5736
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-191-prize-strings.md
@@ -0,0 +1,52 @@
+---
+id: 5900f42b1000cf542c50ff3e
+title: 'Problem 191: Prize Strings'
+challengeType: 1
+forumTopicId: 301829
+dashedName: problem-191-prize-strings
+---
+
+# --description--
+
+A particular school offers cash rewards to children with good attendance and punctuality. If they are absent for three consecutive days or late on more than one occasion then they forfeit their prize.
+
+During an n-day period a trinary string is formed for each child consisting of L's (late), O's (on time), and A's (absent).
+
+Although there are eighty-one trinary strings for a 4-day period that can be formed, exactly forty-three strings would lead to a prize:
+
+```markup
+OOOO OOOA OOOL OOAO OOAA OOAL OOLO OOLA OAOO OAOA
+OAOL OAAO OAAL OALO OALA OLOO OLOA OLAO OLAA AOOO
+AOOA AOOL AOAO AOAA AOAL AOLO AOLA AAOO AAOA AAOL
+AALO AALA ALOO ALOA ALAO ALAA LOOO LOOA LOAO LOAA
+LAOO LAOA LAAO
+```
+
+How many "prize" strings exist over a 30-day period?
+
+# --hints--
+
+`prizeStrings()` should return `1918080160`.
+
+```js
+assert.strictEqual(prizeStrings(), 1918080160);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function prizeStrings() {
+
+ return true;
+}
+
+prizeStrings();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-192-best-approximations.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-192-best-approximations.md
new file mode 100644
index 00000000000..61889d4d47b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-192-best-approximations.md
@@ -0,0 +1,46 @@
+---
+id: 5900f42c1000cf542c50ff3f
+title: 'Problem 192: Best Approximations'
+challengeType: 1
+forumTopicId: 301830
+dashedName: problem-192-best-approximations
+---
+
+# --description--
+
+Let $x$ be a real number.
+
+A best approximation to $x$ for the denominator bound $d$ is a rational number $\frac{r}{s}$ in reduced form, with $s ≤ d$, such that any rational number which is closer to $x$ than $\frac{r}{s}$ has a denominator larger than $d$:
+
+$$|\frac{p}{q} - x| < |\frac{r}{s} - x| ⇒ q > d$$
+
+For example, the best approximation to $\sqrt{13}$ for the denominator bound $20$ is $\frac{18}{5}$ and the best approximation to $\sqrt{13}$ for the denominator bound $30$ is $\frac{101}{28}$.
+
+Find the sum of all denominators of the best approximations to $\sqrt{n}$ for the denominator bound ${10}^{12}$, where $n$ is not a perfect square and $1 < n ≤ 100000$.
+
+# --hints--
+
+`bestApproximations()` should return `57060635927998344`.
+
+```js
+assert.strictEqual(bestApproximations(), 57060635927998344);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function bestApproximations() {
+
+ return true;
+}
+
+bestApproximations();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-193-squarefree-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-193-squarefree-numbers.md
new file mode 100644
index 00000000000..7e17fd27c15
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-193-squarefree-numbers.md
@@ -0,0 +1,40 @@
+---
+id: 5900f42f1000cf542c50ff41
+title: 'Problem 193: Squarefree Numbers'
+challengeType: 1
+forumTopicId: 301831
+dashedName: problem-193-squarefree-numbers
+---
+
+# --description--
+
+A positive integer $n$ is called squarefree, if no square of a prime divides $n$, thus 1, 2, 3, 5, 6, 7, 10, 11 are squarefree, but not 4, 8, 9, 12.
+
+How many squarefree numbers are there below $2^{50}$?
+
+# --hints--
+
+`squarefreeNumbers()` should return `684465067343069`.
+
+```js
+assert.strictEqual(squarefreeNumbers(), 684465067343069);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function squarefreeNumbers() {
+
+ return true;
+}
+
+squarefreeNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-194-coloured-configurations.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-194-coloured-configurations.md
new file mode 100644
index 00000000000..4d5b05af3d9
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-194-coloured-configurations.md
@@ -0,0 +1,46 @@
+---
+id: 5900f42f1000cf542c50ff40
+title: 'Problem 194: Coloured Configurations'
+challengeType: 1
+forumTopicId: 301832
+dashedName: problem-194-coloured-configurations
+---
+
+# --description--
+
+Consider graphs built with the units A:
+
+ and B: 
, where the units are glued along the vertical edges as in the graph 
.
+
+A configuration of type $(a,b,c)$ is a graph thus built of $a$ units A and $b$ units B, where the graph's vertices are coloured using up to $c$ colours, so that no two adjacent vertices have the same colour. The compound graph above is an example of a configuration of type $(2,2,6)$, in fact of type $(2,2,c)$ for all $c ≥ 4$
+
+Let $N(a,b,c)$ be the number of configurations of type $(a,b,c)$. For example, $N(1,0,3) = 24$, $N(0,2,4) = 92928$ and $N(2,2,3) = 20736$.
+
+Find the last 8 digits of $N(25,75,1984)$.
+
+# --hints--
+
+`coloredConfigurations()` should return `61190912`.
+
+```js
+assert.strictEqual(coloredConfigurations(), 61190912);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function coloredConfigurations() {
+
+ return true;
+}
+
+coloredConfigurations();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-195-inscribed-circles-of-triangles-with-one-angle-of-60-degrees.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-195-inscribed-circles-of-triangles-with-one-angle-of-60-degrees.md
new file mode 100644
index 00000000000..18c2acd7592
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-195-inscribed-circles-of-triangles-with-one-angle-of-60-degrees.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4311000cf542c50ff43
+title: 'Problem 195: Inscribed circles of triangles with one angle of 60 degrees'
+challengeType: 1
+forumTopicId: 301833
+dashedName: problem-195-inscribed-circles-of-triangles-with-one-angle-of-60-degrees
+---
+
+# --description--
+
+Let's call an integer sided triangle with exactly one angle of 60° a 60° triangle.
+
+Let $r$ be the radius of the inscribed circle of such a 60° triangle.
+
+There are 1234 60° triangles for which $r ≤ 100$.
+
+Let $T(n)$ be the number of 60° triangles for which $r ≤ n$, so $T(100) = 1234$, $T(1000) = 22767$, and $T(10000) = 359912$.
+
+Find $T(1053779)$.
+
+# --hints--
+
+`inscribedCirclesOfTriangles()` should return `75085391`.
+
+```js
+assert.strictEqual(inscribedCirclesOfTriangles(), 75085391);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function inscribedCirclesOfTriangles() {
+
+ return true;
+}
+
+inscribedCirclesOfTriangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-196-prime-triplets.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-196-prime-triplets.md
new file mode 100644
index 00000000000..d072c7689a1
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-196-prime-triplets.md
@@ -0,0 +1,60 @@
+---
+id: 5900f4301000cf542c50ff42
+title: 'Problem 196: Prime triplets'
+challengeType: 1
+forumTopicId: 301834
+dashedName: problem-196-prime-triplets
+---
+
+# --description--
+
+Build a triangle from all positive integers in the following way:
+
+$$\begin{array}{rrr} & 1 \\\\
+ & \color{red}{2} & \color{red}{3} \\\\ & 4 & \color{red}{5} & 6 \\\\
+ & \color{red}{7} & 8 & 9 & 10 \\\\ & \color{red}{11} & 12 & \color{red}{13} & 14 & 15 \\\\
+ & 16 & \color{red}{17} & 18 & \color{red}{19} & 20 & 21 \\\\ & 22 & \color{red}{23} & 24 & 25 & 26 & 27 & 28 \\\\
+ & \color{red}{29} & 30 & \color{red}{31} & 32 & 33 & 34 & 35 & 36 \\\\ & \color{red}{37} & 38 & 39 & 40 & \color{red}{41} & 42 & \color{red}{43} & 44 & 45 \\\\
+ & 46 & \color{red}{47} & 48 & 49 & 50 & 51 & 52 & \color{red}{53} & 54 & 55 \\\\ & 56 & 57 & 58 & \color{red}{59} & 60 & \color{red}{61} & 62 & 63 & 64 & 65 & 66 \\\\
+ & \cdots \end{array}$$
+
+Each positive integer has up to eight neighbours in the triangle.
+
+A set of three primes is called a prime triplet if one of the three primes has the other two as neighbours in the triangle.
+
+For example, in the second row, the prime numbers 2 and 3 are elements of some prime triplet.
+
+If row 8 is considered, it contains two primes which are elements of some prime triplet, i.e. 29 and 31. If row 9 is considered, it contains only one prime which is an element of some prime triplet: 37.
+
+Define $S(n)$ as the sum of the primes in row $n$ which are elements of any prime triplet. Then $S(8) = 60$ and $S(9) = 37$.
+
+You are given that $S(10000) = 950007619$.
+
+Find $S(5678027) + S(7208785)$.
+
+# --hints--
+
+`primeTriplets()` should return `322303240771079940`.
+
+```js
+assert.strictEqual(primeTriplets(), 322303240771079940);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeTriplets() {
+
+ return true;
+}
+
+primeTriplets();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-197-investigating-the-behaviour-of-a-recursively-defined-sequence.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-197-investigating-the-behaviour-of-a-recursively-defined-sequence.md
new file mode 100644
index 00000000000..608f288e3e9
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-197-investigating-the-behaviour-of-a-recursively-defined-sequence.md
@@ -0,0 +1,40 @@
+---
+id: 5900f4311000cf542c50ff44
+title: 'Problem 197: Investigating the behaviour of a recursively defined sequence'
+challengeType: 1
+forumTopicId: 301835
+dashedName: problem-197-investigating-the-behaviour-of-a-recursively-defined-sequence
+---
+
+# --description--
+
+Given is the function $f(x) = ⌊{2}^{30.403243784 - x^2}⌋ × {10}^{-9}$ ( ⌊ ⌋ is the floor-function), the sequence $u_n$ is defined by $u_0 = -1$ and $u_{n + 1} = f(u_n)$.
+
+Find $u_n + u_{n + 1}$ for $n = {10}^{12}$. Give your answer with 9 digits after the decimal point.
+
+# --hints--
+
+`recursivelyDefinedSequence()` should return `1.710637717`.
+
+```js
+assert.strictEqual(recursivelyDefinedSequence(), 1.710637717);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function recursivelyDefinedSequence() {
+
+ return true;
+}
+
+recursivelyDefinedSequence();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-198-ambiguous-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-198-ambiguous-numbers.md
new file mode 100644
index 00000000000..69c2ba856dc
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-198-ambiguous-numbers.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4331000cf542c50ff45
+title: 'Problem 198: Ambiguous Numbers'
+challengeType: 1
+forumTopicId: 301836
+dashedName: problem-198-ambiguous-numbers
+---
+
+# --description--
+
+A best approximation to a real number $x$ for the denominator bound $d$ is a rational number $\frac{r}{s}$ (in reduced form) with $s ≤ d$, so that any rational number $\frac{p}{q}$ which is closer to $x$ than $\frac{r}{s}$ has $q > d$.
+
+Usually the best approximation to a real number is uniquely determined for all denominator bounds. However, there are some exceptions, e.g. $\frac{9}{40}$ has the two best approximations $\frac{1}{4}$ and $\frac{1}{5}$ for the denominator bound $6$. We shall call a real number $x$ ambiguous, if there is at least one denominator bound for which $x$ possesses two best approximations. Clearly, an ambiguous number is necessarily rational.
+
+How many ambiguous numbers $x = \frac{p}{q}$, $0 < x < \frac{1}{100}$, are there whose denominator $q$ does not exceed ${10}^8$?
+
+# --hints--
+
+`ambiguousNumbers()` should return `52374425`.
+
+```js
+assert.strictEqual(ambiguousNumbers(), 52374425);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function ambiguousNumbers() {
+
+ return true;
+}
+
+ambiguousNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-199-iterative-circle-packing.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-199-iterative-circle-packing.md
new file mode 100644
index 00000000000..5c699d70320
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-199-iterative-circle-packing.md
@@ -0,0 +1,75 @@
+---
+id: 5900f4341000cf542c50ff46
+title: 'Problem 199: Iterative Circle Packing'
+challengeType: 1
+forumTopicId: 301837
+dashedName: problem-199-iterative-circle-packing
+---
+
+# --description--
+
+Three circles of equal radius are placed inside a larger circle such that each pair of circles is tangent to one another and the inner circles do not overlap. There are four uncovered "gaps" which are to be filled iteratively with more tangent circles.
+
+
+
+At each iteration, a maximally sized circle is placed in each gap, which creates more gaps for the next iteration. After 3 iterations (pictured), there are 108 gaps and the fraction of the area which is not covered by circles is 0.06790342, rounded to eight decimal places.
+
+What fraction of the area is not covered by circles after `n` iterations? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
+
+# --hints--
+
+`iterativeCirclePacking(10)` should return a number.
+
+```js
+assert(typeof iterativeCirclePacking(10) === 'number');
+```
+
+`iterativeCirclePacking(10)` should return `0.00396087`.
+
+```js
+assert.strictEqual(iterativeCirclePacking(10), 0.00396087);
+```
+
+`iterativeCirclePacking(3)` should return `0.06790342`.
+
+```js
+assert.strictEqual(iterativeCirclePacking(3), 0.06790342);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function iterativeCirclePacking(n) {
+
+ return true;
+}
+
+iterativeCirclePacking(10);
+```
+
+# --solutions--
+
+```js
+function iterativeCirclePacking(n) {
+ let k1 = 1;
+ let k0 = k1 * (3 - 2 * Math.sqrt(3));
+ let a0 = 1 / (k0 * k0);
+ let a1 = 3 / (k1 * k1);
+ a1 += 3 * getArea(k0, k1, k1, n);
+ a1 += getArea(k1, k1, k1, n);
+ let final = ((a0 - a1) / a0).toFixed(8);
+
+ return parseFloat(final);
+ function getArea(k1, k2, k3, depth) {
+ if (depth == 0) return 0.0;
+ let k4 = k1 + k2 + k3 + 2 * Math.sqrt(k1 * k2 + k2 * k3 + k3 * k1);
+ let a = 1 / (k4 * k4);
+ a += getArea(k1, k2, k4, depth - 1);
+ a += getArea(k2, k3, k4, depth - 1);
+ a += getArea(k3, k1, k4, depth - 1);
+ return a;
+ }
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-200-find-the-200th-prime-proof-sqube-containing-the-contiguous-sub-string-200.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-200-find-the-200th-prime-proof-sqube-containing-the-contiguous-sub-string-200.md
new file mode 100644
index 00000000000..e35cfa0a550
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-101-to-200/problem-200-find-the-200th-prime-proof-sqube-containing-the-contiguous-sub-string-200.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4351000cf542c50ff47
+title: >-
+ Problem 200: Find the 200th prime-proof sqube containing the contiguous sub-string "200"
+challengeType: 1
+forumTopicId: 301840
+dashedName: >-
+ problem-200-find-the-200th-prime-proof-sqube-containing-the-contiguous-sub-string-200
+---
+
+# --description--
+
+We shall define a sqube to be a number of the form, ${p^2}{q^3}$, where $p$ and $q$ are distinct primes.
+
+For example, $200 = {5^2}{2^3}$ or $120072949 = {{23}^2}{{61}^3}$.
+
+The first five squbes are 72, 108, 200, 392, and 500.
+
+Interestingly, 200 is also the first number for which you cannot change any single digit to make a prime; we shall call such numbers, prime-proof. The next prime-proof sqube which contains the contiguous sub-string `200` is 1992008.
+
+Find the 200th prime-proof sqube containing the contiguous sub-string `200`.
+
+# --hints--
+
+`primeProofSqubeWithSubString()` should return `229161792008`.
+
+```js
+assert.strictEqual(primeProofSqubeWithSubString(), 229161792008);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeProofSqubeWithSubString() {
+
+ return true;
+}
+
+primeProofSqubeWithSubString();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-201-subsets-with-a-unique-sum.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-201-subsets-with-a-unique-sum.md
new file mode 100644
index 00000000000..e0513d008ec
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-201-subsets-with-a-unique-sum.md
@@ -0,0 +1,58 @@
+---
+id: 5900f4361000cf542c50ff48
+title: 'Problem 201: Subsets with a unique sum'
+challengeType: 1
+forumTopicId: 301841
+dashedName: problem-201-subsets-with-a-unique-sum
+---
+
+# --description--
+
+For any set $A$ of numbers, let $sum(A)$ be the sum of the elements of $A$.
+
+Consider the set $B = \\{1,3,6,8,10,11\\}$. There are 20 subsets of $B$ containing three elements, and their sums are:
+
+$$\begin{align} & sum(\\{1,3,6\\}) = 10 \\\\
+ & sum(\\{1,3,8\\}) = 12 \\\\ & sum(\\{1,3,10\\}) = 14 \\\\
+ & sum(\\{1,3,11\\}) = 15 \\\\ & sum(\\{1,6,8\\}) = 15 \\\\
+ & sum(\\{1,6,10\\}) = 17 \\\\ & sum(\\{1,6,11\\}) = 18 \\\\
+ & sum(\\{1,8,10\\}) = 19 \\\\ & sum(\\{1,8,11\\}) = 20 \\\\
+ & sum(\\{1,10,11\\}) = 22 \\\\ & sum(\\{3,6,8\\}) = 17 \\\\
+ & sum(\\{3,6,10\\}) = 19 \\\\ & sum(\\{3,6,11\\}) = 20 \\\\
+ & sum(\\{3,8,10\\}) = 21 \\\\ & sum(\\{3,8,11\\}) = 22 \\\\
+ & sum(\\{3,10,11\\}) = 24 \\\\ & sum(\\{6,8,10\\}) = 24 \\\\
+ & sum(\\{6,8,11\\}) = 25 \\\\ & sum(\\{6,10,11\\}) = 27 \\\\
+ & sum(\\{8,10,11\\}) = 29 \\end{align}$$
+
+Some of these sums occur more than once, others are unique. For a set $A$, let $U(A,k)$ be the set of unique sums of $k$-element subsets of $A$, in our example we find $U(B,3) = \\{10,12,14,18,21,25,27,29\\}$ and $sum(U(B,3)) = 156$.
+
+Now consider the $100$-element set $S = \\{1^2, 2^2, \ldots , {100}^2\\}$. $S$ has $100\\,891\\,344\\,545\\,564\\,193\\,334\\,812\\,497\\,256\\;$ $50$-element subsets.
+
+Determine the sum of all integers which are the sum of exactly one of the $50$-element subsets of $S$, i.e. find $sum(U(S,50))$.
+
+# --hints--
+
+`uniqueSubsetsSum()` should return `115039000`.
+
+```js
+assert.strictEqual(uniqueSubsetsSum(), 115039000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function uniqueSubsetsSum() {
+
+ return true;
+}
+
+uniqueSubsetsSum();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-202-laserbeam.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-202-laserbeam.md
new file mode 100644
index 00000000000..2090a152b22
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-202-laserbeam.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4371000cf542c50ff49
+title: 'Problem 202: Laserbeam'
+challengeType: 1
+forumTopicId: 301843
+dashedName: problem-202-laserbeam
+---
+
+# --description--
+
+Three mirrors are arranged in the shape of an equilateral triangle, with their reflective surfaces pointing inwards. There is an infinitesimal gap at each vertex of the triangle through which a laser beam may pass.
+
+Label the vertices $A$, $B$ and $C$. There are 2 ways in which a laser beam may enter vertex $C$, bounce off 11 surfaces, then exit through the same vertex: one way is shown below; the other is the reverse of that.
+
+
+
+There are 80840 ways in which a laser beam may enter vertex $C$, bounce off 1000001 surfaces, then exit through the same vertex.
+
+In how many ways can a laser beam enter at vertex $C$, bounce off 12017639147 surfaces, then exit through the same vertex?
+
+# --hints--
+
+`laserbeam()` should return `1209002624`.
+
+```js
+assert.strictEqual(laserbeam(), 1209002624);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function laserbeam() {
+
+ return true;
+}
+
+laserbeam();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-203-squarefree-binomial-coefficients.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-203-squarefree-binomial-coefficients.md
new file mode 100644
index 00000000000..4e418715771
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-203-squarefree-binomial-coefficients.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4381000cf542c50ff4a
+title: 'Problem 203: Squarefree Binomial Coefficients'
+challengeType: 1
+forumTopicId: 301844
+dashedName: problem-203-squarefree-binomial-coefficients
+---
+
+# --description--
+
+The binomial coefficients $\displaystyle\binom{n}{k}$ can be arranged in triangular form, Pascal's triangle, like this:
+
+$$\begin{array}{ccccccccccccccc} & & & & & & & 1 & & & & & & & \\\\
+ & & & & & & 1 & & 1 & & & & & & \\\\ & & & & & 1 & & 2 & & 1 & & & & & \\\\
+ & & & & 1 & & 3 & & 3 & & 1 & & & & \\\\ & & & 1 & & 4 & & 6 & & 4 & & 1 & & & \\\\
+ & & 1 & & 5 & & 10 & & 10 & & 5 & & 1 & & \\\\ & 1 & & 6 & & 15 & & 20 & & 15 & & 6 & & 1 & \\\\
+ 1 & & 7 & & 21 & & 35 & & 35 & & 21 & & 7 & & 1 \\\\ & & & & & & & \ldots \end{array}$$
+
+It can be seen that the first eight rows of Pascal's triangle contain twelve distinct numbers: 1, 2, 3, 4, 5, 6, 7, 10, 15, 20, 21 and 35.
+
+A positive integer n is called squarefree if no square of a prime divides n. Of the twelve distinct numbers in the first eight rows of Pascal's triangle, all except 4 and 20 are squarefree. The sum of the distinct squarefree numbers in the first eight rows is 105.
+
+Find the sum of the distinct squarefree numbers in the first 51 rows of Pascal's triangle.
+
+# --hints--
+
+`squarefreeBinomialCoefficients()` should return `34029210557338`.
+
+```js
+assert.strictEqual(squarefreeBinomialCoefficients(), 34029210557338);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function squarefreeBinomialCoefficients() {
+
+ return true;
+}
+
+squarefreeBinomialCoefficients();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-204-generalised-hamming-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-204-generalised-hamming-numbers.md
new file mode 100644
index 00000000000..584cf57c132
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-204-generalised-hamming-numbers.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4381000cf542c50ff4b
+title: 'Problem 204: Generalised Hamming Numbers'
+challengeType: 1
+forumTopicId: 301845
+dashedName: problem-204-generalised-hamming-numbers
+---
+
+# --description--
+
+A Hamming number is a positive number which has no prime factor larger than 5.
+
+So the first few Hamming numbers are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15.
+
+There are 1105 Hamming numbers not exceeding ${10}^8$.
+
+We will call a positive number a generalised Hamming number of type $n$, if it has no prime factor larger than $n$. Hence the Hamming numbers are the generalised Hamming numbers of type 5.
+
+How many generalised Hamming numbers of type 100 are there which don't exceed ${10}^9$?
+
+# --hints--
+
+`generalisedHammingNumbers()` should return `2944730`.
+
+```js
+assert.strictEqual(generalisedHammingNumbers(), 2944730);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function generalisedHammingNumbers() {
+
+ return true;
+}
+
+generalisedHammingNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-205-dice-game.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-205-dice-game.md
new file mode 100644
index 00000000000..17614dbf03b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-205-dice-game.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4391000cf542c50ff4c
+title: 'Problem 205: Dice Game'
+challengeType: 1
+forumTopicId: 301846
+dashedName: problem-205-dice-game
+---
+
+# --description--
+
+Peter has nine four-sided (pyramidal) dice, each with faces numbered 1, 2, 3, 4.
+
+Colin has six six-sided (cubic) dice, each with faces numbered 1, 2, 3, 4, 5, 6.
+
+Peter and Colin roll their dice and compare totals: the highest total wins. The result is a draw if the totals are equal.
+
+What is the probability that Pyramidal Pete beats Cubic Colin? Give your answer rounded to seven decimal places in the form 0.abcdefg
+
+# --hints--
+
+`diceGame()` should return `0.5731441`.
+
+```js
+assert.strictEqual(diceGame(), 0.5731441);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function diceGame() {
+
+ return true;
+}
+
+diceGame();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-206-concealed-square.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-206-concealed-square.md
new file mode 100644
index 00000000000..596f703da28
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-206-concealed-square.md
@@ -0,0 +1,63 @@
+---
+id: 5900f43a1000cf542c50ff4d
+title: 'Problem 206: Concealed Square'
+challengeType: 1
+forumTopicId: 301847
+dashedName: problem-206-concealed-square
+---
+
+# --description--
+
+Find the unique positive integer whose square has the form 1_2_3_4_5_6_7_8_9_0, where each "_" is a single digit.
+
+# --hints--
+
+`concealedSquare()` should return `1389019170`.
+
+```js
+assert.strictEqual(concealedSquare(), 1389019170);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function concealedSquare() {
+
+ return true;
+}
+
+concealedSquare();
+```
+
+# --solutions--
+
+```js
+// Check if n**2 matches the pattern
+function squareMatchs(n) {
+ // Need BigInt due to size of values
+ let nSquared = (BigInt(n) * BigInt(n)).toString();
+
+ // Check if digits match pattern
+ for (let i = 1; i <= 9; i++) {
+ if (nSquared[2 * (i - 1)] != i) return false;
+ }
+ return true;
+}
+
+// Find integer whose square matches the pattern
+function concealedSquare() {
+ // Set bounds based upon max and min candidates
+ const minSquareRoot = Math.floor(Math.sqrt(10203040506070809) / 10) * 10;
+ const maxSquareRoot = Math.ceil(Math.sqrt(19293949596979899) / 10) * 10;
+
+ for (let x = maxSquareRoot; x >= minSquareRoot; x -= 10) {
+ // Note: 3*3 = 9 and 7*7 = 49 are only trailing digits
+ // that can produce 9 as trailing digit in square
+ if (squareMatchs(x + 3)) return (x + 3)*10;
+ if (squareMatchs(x + 7)) return (x + 7)*10;
+ }
+ return -1;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-207-integer-partition-equations.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-207-integer-partition-equations.md
new file mode 100644
index 00000000000..29efa6bc5f6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-207-integer-partition-equations.md
@@ -0,0 +1,56 @@
+---
+id: 5900f43c1000cf542c50ff4e
+title: 'Problem 207: Integer partition equations'
+challengeType: 1
+forumTopicId: 301848
+dashedName: problem-207-integer-partition-equations
+---
+
+# --description--
+
+For some positive integers $k$, there exists an integer partition of the form $4^t = 2^t + k$,
+
+where $4^t$, $2^t$, and $k$ are all positive integers and $t$ is a real number.
+
+The first two such partitions are $4^1 = 2^1 + 2$ and $4^{1.584\\,962\\,5\ldots} = 2^{1.584\\,962\\,5\ldots} + 6$.
+
+Partitions where $t$ is also an integer are called perfect. For any $m ≥ 1$ let $P(m)$ be the proportion of such partitions that are perfect with $k ≤ m$.
+
+Thus $P(6) = \frac{1}{2}$.
+
+In the following table are listed some values of $P(m)$
+
+$$\begin{align} & P(5) = \frac{1}{1} \\\\
+ & P(10) = \frac{1}{2} \\\\ & P(15) = \frac{2}{3} \\\\
+ & P(20) = \frac{1}{2} \\\\ & P(25) = \frac{1}{2} \\\\
+ & P(30) = \frac{2}{5} \\\\ & \ldots \\\\
+ & P(180) = \frac{1}{4} \\\\ & P(185) = \frac{3}{13} \end{align}$$
+
+Find the smallest $m$ for which $P(m) < \frac{1}{12\\,345}$
+
+# --hints--
+
+`integerPartitionEquations()` should return `44043947822`.
+
+```js
+assert.strictEqual(integerPartitionEquations(), 44043947822);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function integerPartitionEquations() {
+
+ return true;
+}
+
+integerPartitionEquations();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-208-robot-walks.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-208-robot-walks.md
new file mode 100644
index 00000000000..63c4e63cf53
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-208-robot-walks.md
@@ -0,0 +1,46 @@
+---
+id: 5900f43f1000cf542c50ff51
+title: 'Problem 208: Robot Walks'
+challengeType: 1
+forumTopicId: 301849
+dashedName: problem-208-robot-walks
+---
+
+# --description--
+
+A robot moves in a series of one-fifth circular arcs (72°), with a free choice of a clockwise or an anticlockwise arc for each step, but no turning on the spot.
+
+One of 70932 possible closed paths of 25 arcs starting northward is
+
+
+
+Given that the robot starts facing North, how many journeys of 70 arcs in length can it take that return it, after the final arc, to its starting position?
+
+**Note:** Any arc may be traversed multiple times.
+
+# --hints--
+
+`robotWalks()` should return `331951449665644800`.
+
+```js
+assert.strictEqual(robotWalks(), 331951449665644800);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function robotWalks() {
+
+ return true;
+}
+
+robotWalks();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-209-circular-logic.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-209-circular-logic.md
new file mode 100644
index 00000000000..97190a72f20
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-209-circular-logic.md
@@ -0,0 +1,58 @@
+---
+id: 5900f43e1000cf542c50ff4f
+title: 'Problem 209: Circular Logic'
+challengeType: 1
+forumTopicId: 301850
+dashedName: problem-209-circular-logic
+---
+
+# --description--
+
+A $k$-input binary truth table is a map from $k$ input bits (binary digits, 0 [false] or 1 [true]) to 1 output bit. For example, the $2$-input binary truth tables for the logical $AND$ and $XOR$ functions are:
+
+| x | y | x AND y |
+| - | - | ------- |
+| 0 | 0 | 0 |
+| 0 | 1 | 0 |
+| 1 | 0 | 0 |
+| 1 | 1 | 1 |
+
+| x | y | x XOR y |
+| - | - | ------- |
+| 0 | 0 | 0 |
+| 0 | 1 | 1 |
+| 1 | 0 | 1 |
+| 1 | 1 | 0 |
+
+How many $6$-input binary truth tables, $τ$, satisfy the formula
+
+$$τ(a, b, c, d, e, f) \\; AND \\; τ(b, c, d, e, f, a \\; XOR \\; (b \\; AND \\; c)) = 0$$
+
+for all $6$-bit inputs ($a$, $b$, $c$, $d$, $e$, $f$)?
+
+# --hints--
+
+`circularLogic()` should return `15964587728784`.
+
+```js
+assert.strictEqual(circularLogic(), 15964587728784);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function circularLogic() {
+
+ return true;
+}
+
+circularLogic();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-210-obtuse-angled-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-210-obtuse-angled-triangles.md
new file mode 100644
index 00000000000..0dbbed2f9b0
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-210-obtuse-angled-triangles.md
@@ -0,0 +1,46 @@
+---
+id: 5900f43e1000cf542c50ff50
+title: 'Problem 210: Obtuse Angled Triangles'
+challengeType: 1
+forumTopicId: 301852
+dashedName: problem-210-obtuse-angled-triangles
+---
+
+# --description--
+
+Consider the set $S(r)$ of points ($x$,$y$) with integer coordinates satisfying $|x| + |y| ≤ r$.
+
+Let $O$ be the point (0,0) and $C$ the point ($\frac{r}{4}$,$\frac{r}{4}$).
+
+Let $N(r)$ be the number of points $B$ in $S(r)$, so that the triangle $OBC$ has an obtuse angle, i.e. the largest angle $α$ satisfies $90°<α<180°$.
+
+So, for example, $N(4)=24$ and $N(8)=100$.
+
+What is $N(1\\,000\\,000\\,000)$?
+
+# --hints--
+
+`obtuseAngledTriangles()` should return `1598174770174689500`.
+
+```js
+assert.strictEqual(obtuseAngledTriangles(), 1598174770174689500);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function obtuseAngledTriangles() {
+
+ return true;
+}
+
+obtuseAngledTriangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-211-divisor-square-sum.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-211-divisor-square-sum.md
new file mode 100644
index 00000000000..3dddacaadbb
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-211-divisor-square-sum.md
@@ -0,0 +1,42 @@
+---
+id: 5900f43f1000cf542c50ff52
+title: 'Problem 211: Divisor Square Sum'
+challengeType: 1
+forumTopicId: 301853
+dashedName: problem-211-divisor-square-sum
+---
+
+# --description--
+
+For a positive integer $n$, let $σ_2(n)$ be the sum of the squares of its divisors. For example,
+
+$$σ_2(10) = 1 + 4 + 25 + 100 = 130$$
+
+Find the sum of all $n$, $0 < n < 64\\,000\\,000$ such that $σ_2(n)$ is a perfect square.
+
+# --hints--
+
+`divisorSquareSum()` should return `1922364685`.
+
+```js
+assert.strictEqual(divisorSquareSum(), 1922364685);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function divisorSquareSum() {
+
+ return true;
+}
+
+divisorSquareSum();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-212-combined-volume-of-cuboids.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-212-combined-volume-of-cuboids.md
new file mode 100644
index 00000000000..6fd271c483e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-212-combined-volume-of-cuboids.md
@@ -0,0 +1,57 @@
+---
+id: 5900f4411000cf542c50ff53
+title: 'Problem 212: Combined Volume of Cuboids'
+challengeType: 1
+forumTopicId: 301854
+dashedName: problem-212-combined-volume-of-cuboids
+---
+
+# --description--
+
+An axis-aligned cuboid, specified by parameters $\{ (x_0,y_0,z_0), (dx,dy,dz) \}$, consists of all points ($X$,$Y$,$Z$) such that $x_0 ≤ X ≤ x_0 + dx$, $y_0 ≤ Y ≤ y_0 + dy$ and $z_0 ≤ Z ≤ z_0 + dz$. The volume of the cuboid is the product, $dx × dy × dz$. The combined volume of a collection of cuboids is the volume of their union and will be less than the sum of the individual volumes if any cuboids overlap.
+
+Let $C_1, \ldots, C_{50000}$ be a collection of 50000 axis-aligned cuboids such that $C_n$ has parameters
+
+$$\begin{align} & x_0 = S_{6n - 5} \\; \text{modulo} \\; 10000 \\\\
+ & y_0 = S_{6n - 4} \\; \text{modulo} \\; 10000 \\\\ & z_0 = S_{6n - 3} \\; \text{modulo} \\; 10000 \\\\
+ & dx = 1 + (S_{6n - 2} \\; \text{modulo} \\; 399) \\\\ & dy = 1 + (S_{6n - 1} \\; \text{modulo} \\; 399) \\\\
+ & dz = 1 + (S_{6n} \\; \text{modulo} \\; 399) \\\\ \end{align}$$
+
+where $S_1, \ldots, S_{300000}$ come from the "Lagged Fibonacci Generator":
+
+For $1 ≤ k ≤ 55$, $S_k = [100003 - 200003k + 300007k^3] \\; (modulo \\; 1000000)$
+
+For $56 ≤ k$, $S_k = [S_{k - 24} + S_{k - 55}] \\; (modulo \\; 1000000)$
+
+Thus, $C_1$ has parameters $\{(7,53,183), (94,369,56)\}$, $C_2$ has parameters $\{(2383,3563,5079), (42,212,344)\}$, and so on.
+
+The combined volume of the first 100 cuboids, $C_1, \ldots, C_{100}$, is 723581599.
+
+What is the combined volume of all 50000 cuboids, $C_1, \ldots, C_{50000}$?
+
+# --hints--
+
+`combinedValueOfCuboids()` should return `328968937309`.
+
+```js
+assert.strictEqual(combinedValueOfCuboids(), 328968937309);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function combinedValueOfCuboids() {
+
+ return true;
+}
+
+combinedValueOfCuboids();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-213-flea-circus.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-213-flea-circus.md
new file mode 100644
index 00000000000..a18eb635255
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-213-flea-circus.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4411000cf542c50ff54
+title: 'Problem 213: Flea Circus'
+challengeType: 1
+forumTopicId: 301855
+dashedName: problem-213-flea-circus
+---
+
+# --description--
+
+A 30×30 grid of squares contains 900 fleas, initially one flea per square.
+
+When a bell is rung, each flea jumps to an adjacent square at random (usually 4 possibilities, except for fleas on the edge of the grid or at the corners).
+
+What is the expected number of unoccupied squares after 50 rings of the bell? Give your answer rounded to six decimal places.
+
+# --hints--
+
+`fleaCircus()` should return `330.721154`.
+
+```js
+assert.strictEqual(fleaCircus(), 330.721154);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function fleaCircus() {
+
+ return true;
+}
+
+fleaCircus();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-214-totient-chains.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-214-totient-chains.md
new file mode 100644
index 00000000000..497d541bc82
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-214-totient-chains.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4421000cf542c50ff55
+title: 'Problem 214: Totient Chains'
+challengeType: 1
+forumTopicId: 301856
+dashedName: problem-214-totient-chains
+---
+
+# --description--
+
+Let $φ$ be Euler's totient function, i.e. for a natural number $n$, $φ(n)$ is the number of $k$, $1 ≤ k ≤ n$, for which $gcd(k,n) = 1$.
+
+By iterating $φ$, each positive integer generates a decreasing chain of numbers ending in 1. E.g. if we start with 5 the sequence 5,4,2,1 is generated. Here is a listing of all chains with length 4:
+
+$$\begin{align} 5,4,2,1 & \\\\
+ 7,6,2,1 & \\\\ 8,4,2,1 & \\\\
+ 9,6,2,1 & \\\\ 10,4,2,1 & \\\\
+ 12,4,2,1 & \\\\ 14,6,2,1 & \\\\
+ 18,6,2,1 & \end{align}$$
+
+Only two of these chains start with a prime, their sum is 12.
+
+What is the sum of all primes less than $40\\,000\\,000$ which generate a chain of length 25?
+
+# --hints--
+
+`totientChains()` should return `1677366278943`.
+
+```js
+assert.strictEqual(totientChains(), 1677366278943);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function totientChains() {
+
+ return true;
+}
+
+totientChains();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-215-crack-free-walls.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-215-crack-free-walls.md
new file mode 100644
index 00000000000..4e0f214b938
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-215-crack-free-walls.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4431000cf542c50ff56
+title: 'Problem 215: Crack-free Walls'
+challengeType: 1
+forumTopicId: 301857
+dashedName: problem-215-crack-free-walls
+---
+
+# --description--
+
+Consider the problem of building a wall out of 2×1 and 3×1 bricks (horizontal×vertical dimensions) such that, for extra strength, the gaps between horizontally-adjacent bricks never line up in consecutive layers, i.e. never form a "running crack".
+
+For example, the following 9×3 wall is not acceptable due to the running crack shown in red:
+
+
+
+There are eight ways of forming a crack-free 9×3 wall, written $W(9,3) = 8$.
+
+Calculate $W(32,10)$.
+
+# --hints--
+
+`crackFreeWalls()` should return `806844323190414`.
+
+```js
+assert.strictEqual(crackFreeWalls(), 806844323190414);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function crackFreeWalls() {
+
+ return true;
+}
+
+crackFreeWalls();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
new file mode 100644
index 00000000000..a528915ab9a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4451000cf542c50ff57
+title: 'Problem 216: Investigating the primality of numbers of the form 2n2-1'
+challengeType: 1
+forumTopicId: 301858
+dashedName: problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1
+---
+
+# --description--
+
+Consider numbers $t(n)$ of the form $t(n) = 2n^2 - 1$ with $n > 1$.
+
+The first such numbers are 7, 17, 31, 49, 71, 97, 127 and 161.
+
+It turns out that only $49 = 7 \times 7$ and $161 = 7 \times 23$ are not prime.
+
+For $n ≤ 10000$ there are 2202 numbers $t(n)$ that are prime.
+
+How many numbers $t(n)$ are prime for $n ≤ 50\\,000\\,000$?
+
+# --hints--
+
+`primalityOfNumbers()` should return `5437849`.
+
+```js
+assert.strictEqual(primalityOfNumbers(), 5437849);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primalityOfNumbers() {
+
+ return true;
+}
+
+primalityOfNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-217-balanced-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-217-balanced-numbers.md
new file mode 100644
index 00000000000..f685410fcd3
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-217-balanced-numbers.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4461000cf542c50ff58
+title: 'Problem 217: Balanced Numbers'
+challengeType: 1
+forumTopicId: 301859
+dashedName: problem-217-balanced-numbers
+---
+
+# --description--
+
+A positive integer with $k$ (decimal) digits is called balanced if its first $⌈\frac{k}{2}⌉$ digits sum to the same value as its last $⌈\frac{k}{2}⌉$ digits, where $⌈x⌉$, pronounced ceiling of $x$, is the smallest integer $≥ x$, thus $⌈π⌉ = 4$ and $⌈5⌉ = 5$.
+
+So, for example, all palindromes are balanced, as is 13722.
+
+Let $T(n)$ be the sum of all balanced numbers less than $10^n$.
+
+Thus: $T(1) = 45$, $T(2) = 540$ and $T(5) = 334\\,795\\,890$.
+
+Find $T(47)\\,mod\\,3^{15}$
+
+# --hints--
+
+`balancedNumbers()` should return `6273134`.
+
+```js
+assert.strictEqual(balancedNumbers(), 6273134);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function balancedNumbers() {
+
+ return true;
+}
+
+balancedNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-218-perfect-right-angled-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-218-perfect-right-angled-triangles.md
new file mode 100644
index 00000000000..1d29c005426
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-218-perfect-right-angled-triangles.md
@@ -0,0 +1,56 @@
+---
+id: 5900f4461000cf542c50ff59
+title: 'Problem 218: Perfect right-angled triangles'
+challengeType: 1
+forumTopicId: 301860
+dashedName: problem-218-perfect-right-angled-triangles
+---
+
+# --description--
+
+Consider the right-angled triangle with sides $a=7$, $b=24$ and $c=25$.
+
+The area of this triangle is 84, which is divisible by the perfect numbers 6 and 28.
+
+Moreover it is a primitive right-angled triangle as $gcd(a,b) = 1$ and $gcd(b,c) = 1$.
+
+Also $c$ is a perfect square.
+
+We will call a right-angled triangle perfect if:
+
+- it is a primitive right-angled triangle
+- its hypotenuse is a perfect square
+
+We will call a right-angled triangle super-perfect if:
+
+- it is a perfect right-angled triangle
+- its area is a multiple of the perfect numbers 6 and 28.
+
+How many perfect right-angled triangles with $c ≤ {10}^{16}$ exist that are not super-perfect?
+
+# --hints--
+
+`perfectRightAngledTriangles()` should return `0`.
+
+```js
+assert.strictEqual(perfectRightAngledTriangles(), 0);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function perfectRightAngledTriangles() {
+
+ return true;
+}
+
+perfectRightAngledTriangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-219-skew-cost-coding.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-219-skew-cost-coding.md
new file mode 100644
index 00000000000..f2d2b0f8721
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-219-skew-cost-coding.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4481000cf542c50ff5a
+title: 'Problem 219: Skew-cost coding'
+challengeType: 1
+forumTopicId: 301861
+dashedName: problem-219-skew-cost-coding
+---
+
+# --description--
+
+Let $A$ and $B$ be bit strings (sequences of 0's and 1's).
+
+If $A$ is equal to the leftmost length($A$) bits of $B$, then $A$ is said to be a prefix of $B$.
+
+For example, 00110 is a prefix of 001101001, but not of 00111 or 100110.
+
+A prefix-free code of size $n$ is a collection of $n$ distinct bit strings such that no string is a prefix of any other. For example, this is a prefix-free code of size 6:
+
+$$0000, 0001, 001, 01, 10, 11$$
+
+Now suppose that it costs one penny to transmit a '0' bit, but four pence to transmit a '1'. Then the total cost of the prefix-free code shown above is 35 pence, which happens to be the cheapest possible for the skewed pricing scheme in question. In short, we write $Cost(6) = 35$.
+
+What is $Cost(10^9)$?
+
+# --hints--
+
+`skewCostCoding()` should return `64564225042`.
+
+```js
+assert.strictEqual(skewCostCoding(), 64564225042);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function skewCostCoding() {
+
+ return true;
+}
+
+skewCostCoding();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-220-heighway-dragon.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-220-heighway-dragon.md
new file mode 100644
index 00000000000..e58e3c3f3ec
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-220-heighway-dragon.md
@@ -0,0 +1,57 @@
+---
+id: 5900f4481000cf542c50ff5b
+title: 'Problem 220: Heighway Dragon'
+challengeType: 1
+forumTopicId: 301863
+dashedName: problem-220-heighway-dragon
+---
+
+# --description--
+
+Let $D_0$ be the two-letter string "Fa". For $n ≥ 1$, derive $D_n$ from $D_{n - 1}$ by the string-rewriting rules:
+
+- "a" → "aRbFR"
+- "b" → "LFaLb"
+
+Thus, $D_0$ = "Fa", $D_1$ = "FaRbFR", $D_2$ = "FaRbFRRLFaLbFR", and so on.
+
+These strings can be interpreted as instructions to a computer graphics program, with "F" meaning "draw forward one unit", "L" meaning "turn left 90 degrees", "R" meaning "turn right 90 degrees", and "a" and "b" being ignored. The initial position of the computer cursor is (0,0), pointing up towards (0,1).
+
+Then $D_n$ is an exotic drawing known as the Heighway Dragon of order $n$. For example, $D_{10}$ is shown below; counting each "F" as one step, the highlighted spot at (18,16) is the position reached after 500 steps.
+
+
+
+What is the position of the cursor after ${10}^{12}$ steps in $D_{50}$? Give your answer as a string in the form `x,y` with no spaces.
+
+# --hints--
+
+`heighwayDragon()` should return a string.
+
+```js
+assert(typeof heighwayDragon() === 'string');
+```
+
+`heighwayDragon()` should return the string `139776,963904`.
+
+```js
+assert.strictEqual(heighwayDragon(), '139776,963904');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function heighwayDragon() {
+
+ return true;
+}
+
+heighwayDragon();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-221-alexandrian-integers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-221-alexandrian-integers.md
new file mode 100644
index 00000000000..e7fedf26f75
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-221-alexandrian-integers.md
@@ -0,0 +1,49 @@
+---
+id: 5900f4491000cf542c50ff5c
+title: 'Problem 221: Alexandrian Integers'
+challengeType: 1
+forumTopicId: 301864
+dashedName: problem-221-alexandrian-integers
+---
+
+# --description--
+
+We shall call a positive integer $A$ an "Alexandrian integer", if there exist integers $p$, $q$, $r$ such that:
+
+$$A = p \times q \times r$$
+
+and
+
+$$\frac{1}{A} = \frac{1}{p} + \frac{1}{q} + \frac{1}{r}$$
+
+
+For example, 630 is an Alexandrian integer ($p = 5$, $q = −7$, $r = −18$). In fact, 630 is the 6th Alexandrian integer, the first 6 Alexandrian integers being: 6, 42, 120, 156, 420 and 630.
+
+Find the 150000th Alexandrian integer.
+
+# --hints--
+
+`alexandrianIntegers()` should return `1884161251122450`.
+
+```js
+assert.strictEqual(alexandrianIntegers(), 1884161251122450);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function alexandrianIntegers() {
+
+ return true;
+}
+
+alexandrianIntegers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-222-sphere-packing.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-222-sphere-packing.md
new file mode 100644
index 00000000000..cdb6a9c3977
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-222-sphere-packing.md
@@ -0,0 +1,40 @@
+---
+id: 5900f44b1000cf542c50ff5d
+title: 'Problem 222: Sphere Packing'
+challengeType: 1
+forumTopicId: 301865
+dashedName: problem-222-sphere-packing
+---
+
+# --description--
+
+What is the length of the shortest pipe, of internal radius 50mm, that can fully contain 21 balls of radii 30mm, 31mm, ..., 50mm?
+
+Give your answer in micrometres (${10}^{-6}$ m) rounded to the nearest integer.
+
+# --hints--
+
+`spherePacking()` should return `1590933`.
+
+```js
+assert.strictEqual(spherePacking(), 1590933);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function spherePacking() {
+
+ return true;
+}
+
+spherePacking();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-223-almost-right-angled-triangles-i.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-223-almost-right-angled-triangles-i.md
new file mode 100644
index 00000000000..7fdbc36cbc6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-223-almost-right-angled-triangles-i.md
@@ -0,0 +1,40 @@
+---
+id: 5900f44b1000cf542c50ff5e
+title: 'Problem 223: Almost right-angled triangles I'
+challengeType: 1
+forumTopicId: 301866
+dashedName: problem-223-almost-right-angled-triangles-i
+---
+
+# --description--
+
+Let us call an integer sided triangle with sides $a ≤ b ≤ c$ barely acute if the sides satisfy $a^2 + b^2 = c^2 + 1$.
+
+How many barely acute triangles are there with perimeter $≤ 25\\,000\\,000$?
+
+# --hints--
+
+`almostRightAngledTrianglesOne()` should return `61614848`.
+
+```js
+assert.strictEqual(almostRightAngledTrianglesOne(), 61614848);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function almostRightAngledTrianglesOne() {
+
+ return true;
+}
+
+almostRightAngledTrianglesOne();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-224-almost-right-angled-triangles-ii.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-224-almost-right-angled-triangles-ii.md
new file mode 100644
index 00000000000..c9f9b44cb3f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-224-almost-right-angled-triangles-ii.md
@@ -0,0 +1,40 @@
+---
+id: 5900f44e1000cf542c50ff5f
+title: 'Problem 224: Almost right-angled triangles II'
+challengeType: 1
+forumTopicId: 301867
+dashedName: problem-224-almost-right-angled-triangles-ii
+---
+
+# --description--
+
+Let us call an integer sided triangle with sides $a ≤ b ≤ c$ barely obtuse if the sides satisfy $a^2 + b^2 = c^2 - 1$.
+
+How many barely obtuse triangles are there with perimeter $≤ 75\\,000\\,000$?
+
+# --hints--
+
+`almostRightAngledTrianglesTwo()` should return `4137330`.
+
+```js
+assert.strictEqual(almostRightAngledTrianglesTwo(), 4137330);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function almostRightAngledTrianglesTwo() {
+
+ return true;
+}
+
+almostRightAngledTrianglesTwo();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-225-tribonacci-non-divisors.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-225-tribonacci-non-divisors.md
new file mode 100644
index 00000000000..2221b445314
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-225-tribonacci-non-divisors.md
@@ -0,0 +1,44 @@
+---
+id: 5900f44e1000cf542c50ff60
+title: 'Problem 225: Tribonacci non-divisors'
+challengeType: 1
+forumTopicId: 301868
+dashedName: problem-225-tribonacci-non-divisors
+---
+
+# --description--
+
+The sequence 1, 1, 1, 3, 5, 9, 17, 31, 57, 105, 193, 355, 653, 1201 ...
+
+is defined by $T_1 = T_2 = T_3 = 1$ and $T_n = T_{n - 1} + T_{n - 2} + T_{n - 3}$.
+
+It can be shown that 27 does not divide any terms of this sequence. In fact, 27 is the first odd number with this property.
+
+Find the ${124}^{\text{th}}$ odd number that does not divide any terms of the above sequence.
+
+# --hints--
+
+`tribonacciNonDivisors()` should return `2009`.
+
+```js
+assert.strictEqual(tribonacciNonDivisors(), 2009);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function tribonacciNonDivisors() {
+
+ return true;
+}
+
+tribonacciNonDivisors();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-226-a-scoop-of-blancmange.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-226-a-scoop-of-blancmange.md
new file mode 100644
index 00000000000..fd8031f2594
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-226-a-scoop-of-blancmange.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4511000cf542c50ff62
+title: 'Problem 226: A Scoop of Blancmange'
+challengeType: 1
+forumTopicId: 301869
+dashedName: problem-226-a-scoop-of-blancmange
+---
+
+# --description--
+
+The blancmange curve is the set of points ($x$,$y$) such that $0 ≤ x ≤ 1$ and $\displaystyle y = \sum_{n = 0}^{\infty} \frac{s(2^nx)}{2^n}$, where $s(x)$ is the distance from $x$ to the nearest integer.
+
+The area under the blancmange curve is equal to $\frac{1}{2}$, shown in pink in the diagram below.
+
+
+
+Let $C$ be the circle with centre ($\frac{1}{4}$,$\frac{1}{2}$) and radius $\frac{1}{4}$, shown in black in the diagram.
+
+What area under the blancmange curve is enclosed by $C$? Give your answer rounded to eight decimal places in the form 0.abcdefgh
+
+# --hints--
+
+`scoopOfBlancmange()` should return `0.11316017`.
+
+```js
+assert.strictEqual(scoopOfBlancmange(), 0.11316017);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function scoopOfBlancmange() {
+
+ return true;
+}
+
+scoopOfBlancmange();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-227-the-chase.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-227-the-chase.md
new file mode 100644
index 00000000000..3121c6ac8d8
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-227-the-chase.md
@@ -0,0 +1,50 @@
+---
+id: 5900f44f1000cf542c50ff61
+title: 'Problem 227: The Chase'
+challengeType: 1
+forumTopicId: 301870
+dashedName: problem-227-the-chase
+---
+
+# --description--
+
+"The Chase" is a game played with two dice and an even number of players.
+
+The players sit around a table; the game begins with two opposite players having one die each. On each turn, the two players with a die roll it.
+
+If the player rolls a 1, he passes the die to his neighbour on the left.
+
+If the player rolls a 6, he passes the die to his neighbour on the right.
+
+Otherwise, he keeps the die for the next turn.
+
+The game ends when one player has both dice after they have been rolled and passed; that player has then lost.
+
+In a game with 100 players, what is the expected number of turns the game lasts? Give your answer rounded to ten significant digits.
+
+# --hints--
+
+`theChase()` should return `3780.618622`.
+
+```js
+assert.strictEqual(theChase(), 3780.618622);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function theChase() {
+
+ return true;
+}
+
+theChase();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-228-minkowski-sums.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-228-minkowski-sums.md
new file mode 100644
index 00000000000..3bccd240ed2
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-228-minkowski-sums.md
@@ -0,0 +1,51 @@
+---
+id: 5900f4511000cf542c50ff63
+title: 'Problem 228: Minkowski Sums'
+challengeType: 1
+forumTopicId: 301871
+dashedName: problem-228-minkowski-sums
+---
+
+# --description--
+
+Let $S_n$ be the regular $n$-sided polygon – or shape – whose vertices $v_k (k = 1, 2, \ldots, n)$ have coordinates:
+
+$$\begin{align} & x_k = cos(\frac{2k - 1}{n} × 180°) \\\\
+ & y_k = sin(\frac{2k - 1}{n} × 180°) \end{align}$$
+
+Each $S_n$ is to be interpreted as a filled shape consisting of all points on the perimeter and in the interior.
+
+The Minkowski sum, $S + T$, of two shapes $S$ and $T$ is the result of adding every point in $S$ to every point in $T$, where point addition is performed coordinate-wise: $(u, v) + (x, y) = (u + x, v + y)$.
+
+For example, the sum of $S_3$ and $S_4$ is the six-sided shape shown in pink below:
+
+
+
+How many sides does $S_{1864} + S_{1865} + \ldots + S_{1909}$ have?
+
+# --hints--
+
+`minkowskiSums()` should return `86226`.
+
+```js
+assert.strictEqual(minkowskiSums(), 86226);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function minkowskiSums() {
+
+ return true;
+}
+
+minkowskiSums();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-229-four-representations-using-squares.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-229-four-representations-using-squares.md
new file mode 100644
index 00000000000..3903d30320f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-229-four-representations-using-squares.md
@@ -0,0 +1,56 @@
+---
+id: 5900f4521000cf542c50ff64
+title: 'Problem 229: Four Representations using Squares'
+challengeType: 1
+forumTopicId: 301872
+dashedName: problem-229-four-representations-using-squares
+---
+
+# --description--
+
+Consider the number 3600. It is very special, because
+
+$$\begin{align} & 3600 = {48}^2 + {36}^2 \\\\
+ & 3600 = {20}^2 + {2×40}^2 \\\\ & 3600 = {30}^2 + {3×30}^2 \\\\
+ & 3600 = {45}^2 + {7×15}^2 \\\\ \end{align}$$
+
+Similarly, we find that $88201 = {99}^2 + {280}^2 = {287}^2 + 2 × {54}^2 = {283}^2 + 3 × {52}^2 = {197}^2 + 7 × {84}^2$.
+
+In 1747, Euler proved which numbers are representable as a sum of two squares. We are interested in the numbers $n$ which admit representations of all of the following four types:
+
+$$\begin{align} & n = {a_1}^2 + {b_1}^2 \\\\
+ & n = {a_2}^2 + 2{b_2}^2 \\\\ & n = {a_3}^2 + 3{b_3}^2 \\\\
+ & n = {a_7}^2 + 7{b_7}^2 \\\\ \end{align}$$
+
+where the $a_k$ and $b_k$ are positive integers.
+
+There are 75373 such numbers that do not exceed ${10}^7$.
+
+How many such numbers are there that do not exceed $2 × {10}^9$?
+
+# --hints--
+
+`representationsUsingSquares()` should return `11325263`.
+
+```js
+assert.strictEqual(representationsUsingSquares(), 11325263);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function representationsUsingSquares() {
+
+ return true;
+}
+
+representationsUsingSquares();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-230-fibonacci-words.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-230-fibonacci-words.md
new file mode 100644
index 00000000000..bc6cd70f1cc
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-230-fibonacci-words.md
@@ -0,0 +1,64 @@
+---
+id: 5900f4531000cf542c50ff65
+title: 'Problem 230: Fibonacci Words'
+challengeType: 1
+forumTopicId: 301874
+dashedName: problem-230-fibonacci-words
+---
+
+# --description--
+
+For any two strings of digits, $A$ and $B$, we define $F_{A,B}$ to be the sequence ($A, B, AB, BAB, ABBAB, \ldots$) in which each term is the concatenation of the previous two.
+
+Further, we define $D_{A,B}(n)$ to be the $n^{\text{th}}$ digit in the first term of $F_{A,B}$ that contains at least $n$ digits.
+
+Example:
+
+Let $A = 1\\,415\\,926\\,535$, $B = 8\\,979\\,323\\,846$. We wish to find $D_{A,B}(35)$, say.
+
+The first few terms of $F_{A,B}$ are:
+
+$$\begin{align} & 1\\,415\\,926\\,535 \\\\
+ & 8\\,979\\,323\\,846 \\\\ & 14\\,159\\,265\\,358\\,979\\,323\\,846 \\\\
+ & 897\\,932\\,384\\,614\\,159\\,265\\,358\\,979\\,323\\,846 \\\\ & 14\\,159\\,265\\,358\\,979\\,323\\,846\\,897\\,932\\,384\\,614\\,15\color{red}{9}\\,265\\,358\\,979\\,323\\,846 \end{align}$$
+
+Then $D_{A,B}(35)$ is the ${35}^{\text{th}}$ digit in the fifth term, which is 9.
+
+Now we use for $A$ the first 100 digits of $π$ behind the decimal point:
+
+$$\begin{align} & 14\\,159\\,265\\,358\\,979\\,323\\,846\\,264\\,338\\,327\\,950\\,288\\,419\\,716\\,939\\,937\\,510 \\\\
+ & 58\\,209\\,749\\,445\\,923\\,078\\,164\\,062\\,862\\,089\\,986\\,280\\,348\\,253\\,421\\,170\\,679 \end{align}$$
+
+and for $B$ the next hundred digits:
+
+$$\begin{align} & 82\\,148\\,086\\,513\\,282\\,306\\,647\\,093\\,844\\,609\\,550\\,582\\,231\\,725\\,359\\,408\\,128 \\\\
+ & 48\\,111\\,745\\,028\\,410\\,270\\,193\\,852\\,110\\,555\\,964\\,462\\,294\\,895\\,493\\,038\\,196 \end{align}$$
+
+Find $\sum_{n = 0, 1, \ldots, 17} {10}^n × D_{A,B}((127 + 19n) × 7^n)$.
+
+# --hints--
+
+`fibonacciWords()` should return `850481152593119200`.
+
+```js
+assert.strictEqual(fibonacciWords(), 850481152593119200);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function fibonacciWords() {
+
+ return true;
+}
+
+fibonacciWords();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-231-the-prime-factorisation-of-binomial-coefficients.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-231-the-prime-factorisation-of-binomial-coefficients.md
new file mode 100644
index 00000000000..498810cf48c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-231-the-prime-factorisation-of-binomial-coefficients.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4531000cf542c50ff66
+title: 'Problem 231: The prime factorisation of binomial coefficients'
+challengeType: 1
+forumTopicId: 301875
+dashedName: problem-231-the-prime-factorisation-of-binomial-coefficients
+---
+
+# --description--
+
+The binomial coefficient $\displaystyle\binom{10}{3} = 120$.
+
+$120 = 2^3 × 3 × 5 = 2 × 2 × 2 × 3 × 5$, and $2 + 2 + 2 + 3 + 5 = 14$.
+
+So the sum of the terms in the prime factorisation of $\displaystyle\binom{10}{3}$ is $14$.
+
+Find the sum of the terms in the prime factorisation of $\binom{20\\,000\\,000}{15\\,000\\,000}$.
+
+# --hints--
+
+`primeFactorisation()` should return `7526965179680`.
+
+```js
+assert.strictEqual(primeFactorisation(), 7526965179680);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeFactorisation() {
+
+ return true;
+}
+
+primeFactorisation();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-232-the-race.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-232-the-race.md
new file mode 100644
index 00000000000..c03c0d687b3
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-232-the-race.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4551000cf542c50ff67
+title: 'Problem 232: The Race'
+challengeType: 1
+forumTopicId: 301876
+dashedName: problem-232-the-race
+---
+
+# --description--
+
+Two players share an unbiased coin and take it in turns to play "The Race".
+
+On Player 1's turn, he tosses the coin once: if it comes up Heads, he scores one point; if it comes up Tails, he scores nothing.
+
+On Player 2's turn, she chooses a positive integer $T$ and tosses the coin $T$ times: if it comes up all Heads, she scores $2^{T - 1}$ points; otherwise, she scores nothing.
+
+Player 1 goes first. The winner is the first to 100 or more points.
+
+On each turn Player 2 selects the number, $T$, of coin tosses that maximises the probability of her winning.
+
+What is the probability that Player 2 wins?
+
+Give your answer rounded to eight decimal places in the form 0.abcdefgh .
+
+# --hints--
+
+`theRace()` should return `0.83648556`.
+
+```js
+assert.strictEqual(theRace(), 0.83648556);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function theRace() {
+
+ return true;
+}
+
+theRace();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-233-lattice-points-on-a-circle.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-233-lattice-points-on-a-circle.md
new file mode 100644
index 00000000000..db650947233
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-233-lattice-points-on-a-circle.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4551000cf542c50ff68
+title: 'Problem 233: Lattice points on a circle'
+challengeType: 1
+forumTopicId: 301877
+dashedName: problem-233-lattice-points-on-a-circle
+---
+
+# --description--
+
+Let $f(N)$ be the number of points with integer coordinates that are on a circle passing through $(0,0)$, $(N,0)$,$(0,N)$, and $(N,N)$.
+
+It can be shown that $f(10000) = 36$.
+
+What is the sum of all positive integers $N ≤ {10}^{11}$ such that $f(N) = 420$?
+
+# --hints--
+
+`latticePointsOnACircle()` should return `271204031455541300`.
+
+```js
+assert.strictEqual(latticePointsOnACircle(), 271204031455541300);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function latticePointsOnACircle() {
+
+ return true;
+}
+
+latticePointsOnACircle();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-234-semidivisible-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-234-semidivisible-numbers.md
new file mode 100644
index 00000000000..ec01ca36a28
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-234-semidivisible-numbers.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4571000cf542c50ff69
+title: 'Problem 234: Semidivisible numbers'
+challengeType: 1
+forumTopicId: 301878
+dashedName: problem-234-semidivisible-numbers
+---
+
+# --description--
+
+For an integer $n ≥ 4$, we define the lower prime square root of $n$, denoted by $lps(n)$, as the $\text{largest prime} ≤ \sqrt{n}$ and the upper prime square root of $n$, $ups(n)$, as the $\text{smallest prime} ≥ \sqrt{n}$.
+
+So, for example, $lps(4) = 2 = ups(4)$, $lps(1000) = 31$, $ups(1000) = 37$.
+
+Let us call an integer $n ≥ 4$ semidivisible, if one of $lps(n)$ and $ups(n)$ divides $n$, but not both.
+
+The sum of the semidivisible numbers not exceeding 15 is 30, the numbers are 8, 10 and 12. 15 is not semidivisible because it is a multiple of both $lps(15) = 3$ and $ups(15) = 5$. As a further example, the sum of the 92 semidivisible numbers up to 1000 is 34825.
+
+What is the sum of all semidivisible numbers not exceeding 999966663333?
+
+# --hints--
+
+`semidivisibleNumbers()` should return `1259187438574927000`.
+
+```js
+assert.strictEqual(semidivisibleNumbers(), 1259187438574927000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function semidivisibleNumbers() {
+
+ return true;
+}
+
+semidivisibleNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-235-an-arithmetic-geometric-sequence.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-235-an-arithmetic-geometric-sequence.md
new file mode 100644
index 00000000000..893687367a5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-235-an-arithmetic-geometric-sequence.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4571000cf542c50ff6a
+title: 'Problem 235: An Arithmetic Geometric sequence'
+challengeType: 1
+forumTopicId: 301879
+dashedName: problem-235-an-arithmetic-geometric-sequence
+---
+
+# --description--
+
+Given is the arithmetic-geometric sequence $u(k) = (900 - 3k)r^{k - 1}$.
+
+Let $s(n) = \sum_{k=1 \ldots n} u(k)$.
+
+Find the value of $r$ for which $s(5000) = -600\\,000\\,000\\,000$.
+
+Give your answer rounded to 12 places behind the decimal point.
+
+# --hints--
+
+`arithmeticGeometricSequence()` should return `1.002322108633`.
+
+```js
+assert.strictEqual(arithmeticGeometricSequence(), 1.002322108633);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function arithmeticGeometricSequence() {
+
+ return true;
+}
+
+arithmeticGeometricSequence();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-236-luxury-hampers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-236-luxury-hampers.md
new file mode 100644
index 00000000000..2ae12a0ab04
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-236-luxury-hampers.md
@@ -0,0 +1,65 @@
+---
+id: 5900f4591000cf542c50ff6b
+title: 'Problem 236: Luxury Hampers'
+challengeType: 1
+forumTopicId: 301881
+dashedName: problem-236-luxury-hampers
+---
+
+# --description--
+
+Suppliers 'A' and 'B' provided the following numbers of products for the luxury hamper market:
+
+| Product | 'A' | 'B' |
+| ------------------ | ---- | ---- |
+| Beluga Caviar | 5248 | 640 |
+| Christmas Cake | 1312 | 1888 |
+| Gammon Joint | 2624 | 3776 |
+| Vintage Port | 5760 | 3776 |
+| Champagne Truffles | 3936 | 5664 |
+
+Although the suppliers try very hard to ship their goods in perfect condition, there is inevitably some spoilage - i.e. products gone bad.
+
+The suppliers compare their performance using two types of statistic:
+
+- The five per-product spoilage rates for each supplier are equal to the number of products gone bad divided by the number of products supplied, for each of the five products in turn.
+- The overall spoilage rate for each supplier is equal to the total number of products gone bad divided by the total number of products provided by that supplier.
+
+To their surprise, the suppliers found that each of the five per-product spoilage rates was worse (higher) for 'B' than for 'A' by the same factor (ratio of spoilage rates), $m > 1$; and yet, paradoxically, the overall spoilage rate was worse for 'A' than for 'B', also by a factor of $m$.
+
+There are thirty-five $m > 1$ for which this surprising result could have occurred, the smallest of which is $\frac{1476}{1475}$.
+
+What's the largest possible value of $m$? Give your answer as a string with fraction reduced to its lowest terms, in the form `u/v`.
+
+# --hints--
+
+`luxuryHampers()` should return a string.
+
+```js
+assert(typeof luxuryHampers() === 'string');
+```
+
+`luxuryHampers()` should return the string `123/59`.
+
+```js
+assert.strictEqual(luxuryHampers(), '123/59');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function luxuryHampers() {
+
+ return true;
+}
+
+luxuryHampers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-237-tours-on-a-4-x-n-playing-board.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-237-tours-on-a-4-x-n-playing-board.md
new file mode 100644
index 00000000000..ef7c2a30c04
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-237-tours-on-a-4-x-n-playing-board.md
@@ -0,0 +1,49 @@
+---
+id: 5900f4591000cf542c50ff6c
+title: 'Problem 237: Tours on a 4 x n playing board'
+challengeType: 1
+forumTopicId: 301882
+dashedName: problem-237-tours-on-a-4-x-n-playing-board
+---
+
+# --description--
+
+Let $T(n)$ be the number of tours over a 4 × $n$ playing board such that:
+
+- The tour starts in the top left corner.
+- The tour consists of moves that are up, down, left, or right one square.
+- The tour visits each square exactly once.
+- The tour ends in the bottom left corner.
+
+The diagram shows one tour over a 4 × 10 board:
+
+
+
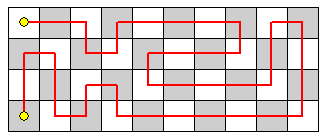+$T(10)$ is 2329. What is $T({10}^{12})$ modulo ${10}^8$?
+
+# --hints--
+
+`toursOnPlayingBoard()` should return `15836928`.
+
+```js
+assert.strictEqual(toursOnPlayingBoard(), 15836928);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function toursOnPlayingBoard() {
+
+ return true;
+}
+
+toursOnPlayingBoard();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-238-infinite-string-tour.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-238-infinite-string-tour.md
new file mode 100644
index 00000000000..6f49452d838
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-238-infinite-string-tour.md
@@ -0,0 +1,59 @@
+---
+id: 5900f45b1000cf542c50ff6d
+title: 'Problem 238: Infinite string tour'
+challengeType: 1
+forumTopicId: 301883
+dashedName: problem-238-infinite-string-tour
+---
+
+# --description--
+
+Create a sequence of numbers using the "Blum Blum Shub" pseudo-random number generator:
+
+$$ s_0 = 14025256 \\\\
+s_{n + 1} = {s_n}^2 \\; mod \\; 20\\,300\\,713 $$
+
+Concatenate these numbers $s_0s_1s_2\ldots$ to create a string $w$ of infinite length. Then, $w = 14025256741014958470038053646\ldots$
+
+For a positive integer $k$, if no substring of $w$ exists with a sum of digits equal to $k$, $p(k)$ is defined to be zero. If at least one substring of $w$ exists with a sum of digits equal to $k$, we define $p(k) = z$, where $z$ is the starting position of the earliest such substring.
+
+For instance:
+
+The substrings 1, 14, 1402, … with respective sums of digits equal to 1, 5, 7, … start at position 1, hence $p(1) = p(5) = p(7) = \ldots = 1$.
+
+The substrings 4, 402, 4025, … with respective sums of digits equal to 4, 6, 11, … start at position 2, hence $p(4) = p(6) = p(11) = \ldots = 2$.
+
+The substrings 02, 0252, … with respective sums of digits equal to 2, 9, … start at position 3, hence $p(2) = p(9) = \ldots = 3$.
+
+Note that substring 025 starting at position 3, has a sum of digits equal to 7, but there was an earlier substring (starting at position 1) with a sum of digits equal to 7, so $p(7) = 1$, not 3.
+
+We can verify that, for $0 < k ≤ {10}^3$, $\sum p(k) = 4742$.
+
+Find $\sum p(k)$, for $0 < k ≤ 2 \times {10}^{15}$.
+
+# --hints--
+
+`infiniteStringTour()` should return `9922545104535660`.
+
+```js
+assert.strictEqual(infiniteStringTour(), 9922545104535660);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function infiniteStringTour() {
+
+ return true;
+}
+
+infiniteStringTour();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-239-twenty-two-foolish-primes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-239-twenty-two-foolish-primes.md
new file mode 100644
index 00000000000..9fff8274ba8
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-239-twenty-two-foolish-primes.md
@@ -0,0 +1,42 @@
+---
+id: 5900f45c1000cf542c50ff6e
+title: 'Problem 239: Twenty-two Foolish Primes'
+challengeType: 1
+forumTopicId: 301884
+dashedName: problem-239-twenty-two-foolish-primes
+---
+
+# --description--
+
+A set of disks numbered 1 through 100 are placed in a line in random order.
+
+What is the probability that we have a partial derangement such that exactly 22 prime number discs are found away from their natural positions? (Any number of non-prime disks may also be found in or out of their natural positions.)
+
+Give your answer rounded to 12 places behind the decimal point in the form 0.abcdefghijkl.
+
+# --hints--
+
+`twentyTwoFoolishPrimes()` should return `0.001887854841`.
+
+```js
+assert.strictEqual(twentyTwoFoolishPrimes(), 0.001887854841);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function twentyTwoFoolishPrimes() {
+
+ return true;
+}
+
+twentyTwoFoolishPrimes();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-240-top-dice.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-240-top-dice.md
new file mode 100644
index 00000000000..97f89f17305
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-240-top-dice.md
@@ -0,0 +1,44 @@
+---
+id: 5900f45d1000cf542c50ff6f
+title: 'Problem 240: Top Dice'
+challengeType: 1
+forumTopicId: 301887
+dashedName: problem-240-top-dice
+---
+
+# --description--
+
+There are 1111 ways in which five 6-sided dice (sides numbered 1 to 6) can be rolled so that the top three sum to 15. Some examples are:
+
+$$\begin{align} & D_1,D_2,D_3,D_4,D_5 = 4,3,6,3,5 \\\\
+ & D_1,D_2,D_3,D_4,D_5 = 4,3,3,5,6 \\\\ & D_1,D_2,D_3,D_4,D_5 = 3,3,3,6,6 \\\\
+ & D_1,D_2,D_3,D_4,D_5 = 6,6,3,3,3 \end{align}$$
+
+In how many ways can twenty 12-sided dice (sides numbered 1 to 12) be rolled so that the top ten sum to 70?
+
+# --hints--
+
+`topDice()` should return `7448717393364182000`.
+
+```js
+assert.strictEqual(topDice(), 7448717393364182000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function topDice() {
+
+ return true;
+}
+
+topDice();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-241-perfection-quotients.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-241-perfection-quotients.md
new file mode 100644
index 00000000000..492d3f61f8e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-241-perfection-quotients.md
@@ -0,0 +1,44 @@
+---
+id: 5900f45d1000cf542c50ff70
+title: 'Problem 241: Perfection Quotients'
+challengeType: 1
+forumTopicId: 301888
+dashedName: problem-241-perfection-quotients
+---
+
+# --description--
+
+For a positive integer $n$, let $σ(n)$ be the sum of all divisors of $n$, so e.g. $σ(6) = 1 + 2 + 3 + 6 = 12$.
+
+A perfect number, as you probably know, is a number with $σ(n) = 2n$.
+
+Let us define the perfection quotient of a positive integer as $p(n) = \frac{σ(n)}{n}$.
+
+Find the sum of all positive integers $n ≤ {10}^{18}$ for which $p(n)$ has the form $k + \frac{1}{2}$, where $k$ is an integer.
+
+# --hints--
+
+`perfectionQuotients()` should return `482316491800641150`.
+
+```js
+assert.strictEqual(perfectionQuotients(), 482316491800641150);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function perfectionQuotients() {
+
+ return true;
+}
+
+perfectionQuotients();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-242-odd-triplets.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-242-odd-triplets.md
new file mode 100644
index 00000000000..abbcfca2a6a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-242-odd-triplets.md
@@ -0,0 +1,44 @@
+---
+id: 5900f45f1000cf542c50ff71
+title: 'Problem 242: Odd Triplets'
+challengeType: 1
+forumTopicId: 301889
+dashedName: problem-242-odd-triplets
+---
+
+# --description--
+
+Given the set {1,2,..., $n$}, we define $f(n, k)$ as the number of its $k$-element subsets with an odd sum of elements. For example, $f(5,3) = 4$, since the set {1,2,3,4,5} has four 3-element subsets having an odd sum of elements, i.e.: {1,2,4}, {1,3,5}, {2,3,4} and {2,4,5}.
+
+When all three values $n$, $k$ and $f(n, k)$ are odd, we say that they make an odd-triplet $[n, k, f(n, k)]$.
+
+There are exactly five odd-triplets with $n ≤ 10$, namely: $[1, 1, f(1, 1) = 1]$, $[5, 1, f(5, 1) = 3]$, $[5, 5, f(5, 5) = 1]$, $[9, 1, f(9, 1) = 5]$ and $[9, 9, f(9, 9) = 1]$.
+
+How many odd-triplets are there with $n ≤ {10}^{12}$?
+
+# --hints--
+
+`oddTriplets()` should return `997104142249036700`.
+
+```js
+assert.strictEqual(oddTriplets(), 997104142249036700);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function oddTriplets() {
+
+ return true;
+}
+
+oddTriplets();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-243-resilience.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-243-resilience.md
new file mode 100644
index 00000000000..67287eac731
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-243-resilience.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4601000cf542c50ff73
+title: 'Problem 243: Resilience'
+challengeType: 1
+forumTopicId: 301890
+dashedName: problem-243-resilience
+---
+
+# --description--
+
+A positive fraction whose numerator is less than its denominator is called a proper fraction.
+
+For any denominator, $d$, there will be $d−1$ proper fractions; for example, with $d = 12$:
+
+$$\frac{1}{12}, \frac{2}{12}, \frac{3}{12}, \frac{4}{12}, \frac{5}{12}, \frac{6}{12}, \frac{7}{12}, \frac{8}{12}, \frac{9}{12}, \frac{10}{12}, \frac{11}{12}$$
+
+We shall call a fraction that cannot be cancelled down a resilient fraction.
+
+Furthermore we shall define the resilience of a denominator, $R(d)$, to be the ratio of its proper fractions that are resilient; for example, $R(12) = \frac{4}{11}$.
+
+In fact, $d = 12$ is the smallest denominator having a resilience $R(d) < \frac{4}{10}$.
+
+Find the smallest denominator $d$, having a resilience $R(d) < \frac{15\\,499}{94\\,744}$.
+
+# --hints--
+
+`resilience()` should return `892371480`.
+
+```js
+assert.strictEqual(resilience(), 892371480);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function resilience() {
+
+ return true;
+}
+
+resilience();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-244-sliders.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-244-sliders.md
new file mode 100644
index 00000000000..ebe4a76b838
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-244-sliders.md
@@ -0,0 +1,58 @@
+---
+id: 5900f4601000cf542c50ff72
+title: 'Problem 244: Sliders'
+challengeType: 1
+forumTopicId: 301891
+dashedName: problem-244-sliders
+---
+
+# --description--
+
+You probably know the game Fifteen Puzzle. Here, instead of numbered tiles, we have seven red tiles and eight blue tiles.
+
+A move is denoted by the uppercase initial of the direction (Left, Right, Up, Down) in which the tile is slid, e.g. starting from configuration ($S$), by the sequence $LULUR$ we reach the configuration ($E$):
+
+($S$) 
, ($E$) 
+
+For each path, its checksum is calculated by (pseudocode):
+
+$$\begin{align} & \text{checksum} = 0 \\\\
+ & \text{checksum} = (\text{checksum} × 243 + m_1) \\; \text{mod} \\; 100\\,000\\,007 \\\\ & \text{checksum} = (\text{checksum} × 243 + m_2) \\; \text{mod} \\; 100\\,000\\,007 \\\\
+ & \ldots \\\\ & \text{checksum} = (\text{checksum} × 243 + m_n) \\; \text{mod} \\; 100\\,000\\,007 \end{align}$$
+
+where $m_k$ is the ASCII value of the $k^{\text{th}}$ letter in the move sequence and the ASCII values for the moves are:
+
+$$\begin{array}{|c|c|} \hline L & 76 \\\\ \hline R & 82 \\\\ \hline U & 85 \\\\ \hline D & 68 \\\\ \hline \end{array}$$
+
+For the sequence $LULUR$ given above, the checksum would be 19761398. Now, starting from configuration ($S$), find all shortest ways to reach configuration ($T$).
+
+($S$) 
, ($T$) 
+
+What is the sum of all checksums for the paths having the minimal length?
+
+# --hints--
+
+`sliders()` should return `96356848`.
+
+```js
+assert.strictEqual(sliders(), 96356848);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sliders() {
+
+ return true;
+}
+
+sliders();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-245-coresilience.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-245-coresilience.md
new file mode 100644
index 00000000000..c3e090d0edb
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-245-coresilience.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4621000cf542c50ff74
+title: 'Problem 245: Coresilience'
+challengeType: 1
+forumTopicId: 301892
+dashedName: problem-245-coresilience
+---
+
+# --description--
+
+We shall call a fraction that cannot be cancelled down a resilient fraction.
+
+Furthermore we shall define the resilience of a denominator, $R(d)$, to be the ratio of its proper fractions that are resilient; for example, $R(12) = \frac{4}{11}$.
+
+The resilience of a number $d > 1$ is then $\frac{φ(d)}{d − 1}$ , where $φ$ is Euler's totient function.
+
+We further define the coresilience of a number $n > 1$ as $C(n) = \frac{n − φ(n)}{n − 1}$.
+
+The coresilience of a prime $p$ is $C(p) = \frac{1}{p − 1}$.
+
+Find the sum of all composite integers $1 < n ≤ 2 × {10}^{11}$, for which $C(n)$ is a unit fraction.
+
+# --hints--
+
+`coresilience()` should return `288084712410001`.
+
+```js
+assert.strictEqual(coresilience(), 288084712410001);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function coresilience() {
+
+ return true;
+}
+
+coresilience();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-246-tangents-to-an-ellipse.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-246-tangents-to-an-ellipse.md
new file mode 100644
index 00000000000..16c5d89e23b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-246-tangents-to-an-ellipse.md
@@ -0,0 +1,58 @@
+---
+id: 5900f4621000cf542c50ff75
+title: 'Problem 246: Tangents to an ellipse'
+challengeType: 1
+forumTopicId: 301893
+dashedName: problem-246-tangents-to-an-ellipse
+---
+
+# --description--
+
+A definition for an ellipse is:
+
+Given a circle $c$ with centre $M$ and radius $r$ and a point $G$ such that $d(G, M) < r$, the locus of the points that are equidistant from $c$ and $G$ form an ellipse.
+
+The construction of the points of the ellipse is shown below.
+
+
+
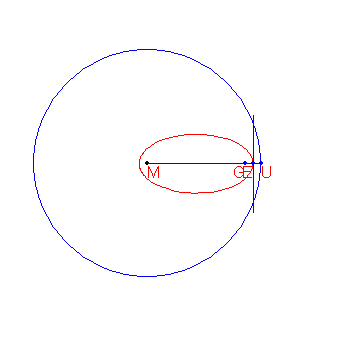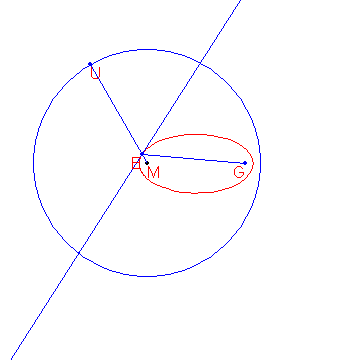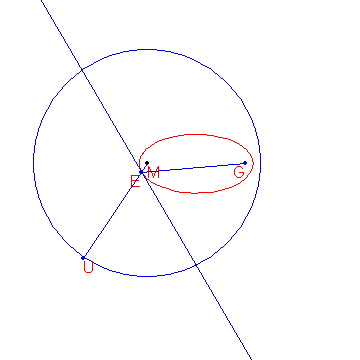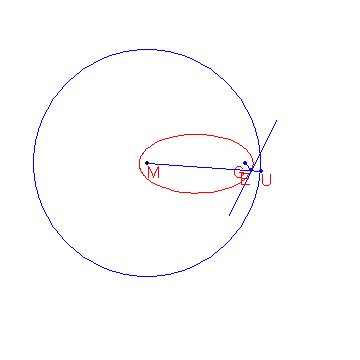+Given are the points $M(-2000, 1500)$ and $G(8000, 1500)$.
+
+Given is also the circle $c$ with centre $M$ and radius $15\\,000$.
+
+The locus of the points that are equidistant from $G$ and $c$ form an ellipse $e$.
+
+From a point $P$ outside $e$ the two tangents $t_1$ and $t_2$ to the ellipse are drawn.
+
+Let the points where $t_1$ and $t_2$ touch the ellipse be $R$ and $S$.
+
+
+
+For how many lattice points $P$ is angle $RPS$ greater than 45°?
+
+# --hints--
+
+`tangentsToAnEllipse()` should return `810834388`.
+
+```js
+assert.strictEqual(tangentsToAnEllipse(), 810834388);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function tangentsToAnEllipse() {
+
+ return true;
+}
+
+tangentsToAnEllipse();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-247-squares-under-a-hyperbola.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-247-squares-under-a-hyperbola.md
new file mode 100644
index 00000000000..d84036f8701
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-247-squares-under-a-hyperbola.md
@@ -0,0 +1,56 @@
+---
+id: 5900f4641000cf542c50ff76
+title: 'Problem 247: Squares under a hyperbola'
+challengeType: 1
+forumTopicId: 301894
+dashedName: problem-247-squares-under-a-hyperbola
+---
+
+# --description--
+
+Consider the region constrained by $1 ≤ x$ and $0 ≤ y ≤ \frac{1}{x}$.
+
+Let $S_1$ be the largest square that can fit under the curve.
+
+Let $S_2$ be the largest square that fits in the remaining area, and so on.
+
+Let the index of $S_n$ be the pair (left, below) indicating the number of squares to the left of $S_n$ and the number of squares below $S_n$.
+
+
+
+The diagram shows some such squares labelled by number.
+
+$S_2$ has one square to its left and none below, so the index of $S_2$ is (1, 0).
+
+It can be seen that the index of $S_{32}$ is (1,1) as is the index of $S_{50}$.
+
+50 is the largest $n$ for which the index of $S_n$ is (1, 1).
+
+What is the largest $n$ for which the index of $S_n$ is (3, 3)?
+
+# --hints--
+
+`squaresUnderAHyperbola()` should return `782252`.
+
+```js
+assert.strictEqual(squaresUnderAHyperbola(), 782252);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function squaresUnderAHyperbola() {
+
+ return true;
+}
+
+squaresUnderAHyperbola();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-248-numbers-for-which-eulers-totient-function-equals-13.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-248-numbers-for-which-eulers-totient-function-equals-13.md
new file mode 100644
index 00000000000..0df6dd5226a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-248-numbers-for-which-eulers-totient-function-equals-13.md
@@ -0,0 +1,40 @@
+---
+id: 5900f4651000cf542c50ff77
+title: 'Problem 248: Numbers for which Euler’s totient function equals 13!'
+challengeType: 1
+forumTopicId: 301895
+dashedName: problem-248-numbers-for-which-eulers-totient-function-equals-13
+---
+
+# --description--
+
+The first number $n$ for which $φ(n) = 13!$ is $6\\,227\\,180\\,929$.
+
+Find the ${150\\,000}^{\text{th}}$ such number.
+
+# --hints--
+
+`eulersTotientFunctionEquals()` should return `23507044290`.
+
+```js
+assert.strictEqual(eulersTotientFunctionEquals(), 23507044290);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function eulersTotientFunctionEquals() {
+
+ return true;
+}
+
+eulersTotientFunctionEquals();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-249-prime-subset-sums.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-249-prime-subset-sums.md
new file mode 100644
index 00000000000..09232c7c178
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-249-prime-subset-sums.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4671000cf542c50ff79
+title: 'Problem 249: Prime Subset Sums'
+challengeType: 1
+forumTopicId: 301896
+dashedName: problem-249-prime-subset-sums
+---
+
+# --description--
+
+Let $S = \\{2, 3, 5, \ldots, 4999\\}$ be the set of prime numbers less than 5000.
+
+Find the number of subsets of $S$, the sum of whose elements is a prime number.
+
+Enter the rightmost 16 digits as your answer.
+
+# --hints--
+
+`primeSubsetSums()` should return `9275262564250418`.
+
+```js
+assert.strictEqual(primeSubsetSums(), 9275262564250418);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeSubsetSums() {
+
+ return true;
+}
+
+primeSubsetSums();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-250-250250.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-250-250250.md
new file mode 100644
index 00000000000..c526154b6e7
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-250-250250.md
@@ -0,0 +1,38 @@
+---
+id: 5900f4661000cf542c50ff78
+title: 'Problem 250: 250250'
+challengeType: 1
+forumTopicId: 301898
+dashedName: problem-250-250250
+---
+
+# --description--
+
+Find the number of non-empty subsets of $\\{{1}^{1}, {2}^{2}, {3}^{3}, \ldots, {250250}^{250250}\\}$, the sum of whose elements is divisible by 250. Enter the rightmost 16 digits as your answer.
+
+# --hints--
+
+`twoHundredFifty()` should return `1425480602091519`.
+
+```js
+assert.strictEqual(twoHundredFifty(), 1425480602091519);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function twoHundredFifty() {
+
+ return true;
+}
+
+twoHundredFifty();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-251-cardano-triplets.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-251-cardano-triplets.md
new file mode 100644
index 00000000000..8f4013595f3
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-251-cardano-triplets.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4671000cf542c50ff7a
+title: 'Problem 251: Cardano Triplets'
+challengeType: 1
+forumTopicId: 301899
+dashedName: problem-251-cardano-triplets
+---
+
+# --description--
+
+A triplet of positive integers ($a$,$b$,$c$) is called a Cardano Triplet if it satisfies the condition:
+
+$$\sqrt[3]{a + b \sqrt{c}} + \sqrt[3]{a - b \sqrt{c}} = 1$$
+
+For example, (2,1,5) is a Cardano Triplet.
+
+There exist 149 Cardano Triplets for which $a + b + c ≤ 1000$.
+
+Find how many Cardano Triplets exist such that $a + b + c ≤ 110\\,000\\,000$.
+
+# --hints--
+
+`cardanoTriplets()` should return `18946051`.
+
+```js
+assert.strictEqual(cardanoTriplets(), 18946051);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function cardanoTriplets() {
+
+ return true;
+}
+
+cardanoTriplets();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-252-convex-holes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-252-convex-holes.md
new file mode 100644
index 00000000000..ec671c067aa
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-252-convex-holes.md
@@ -0,0 +1,51 @@
+---
+id: 5900f4691000cf542c50ff7b
+title: 'Problem 252: Convex Holes'
+challengeType: 1
+forumTopicId: 301900
+dashedName: problem-252-convex-holes
+---
+
+# --description--
+
+Given a set of points on a plane, we define a convex hole to be a convex polygon having as vertices any of the given points and not containing any of the given points in its interior (in addition to the vertices, other given points may lie on the perimeter of the polygon).
+
+As an example, the image below shows a set of twenty points and a few such convex holes. The convex hole shown as a red heptagon has an area equal to 1049694.5 square units, which is the highest possible area for a convex hole on the given set of points.
+
+
+
+For our example, we used the first 20 points ($T_{2k − 1}$, $T_{2k}$), for $k = 1, 2, \ldots, 20$, produced with the pseudo-random number generator:
+
+$$\begin{align} S_0 & = 290\\,797 \\\\
+ S_{n+1} & = {S_n}^2 \\; \text{mod} \\; 50\\,515\\,093 \\\\ T_n & = (S_n \\; \text{mod} \\; 2000) − 1000 \end{align}$$
+
+i.e. (527, 144), (−488, 732), (−454, −947), …
+
+What is the maximum area for a convex hole on the set containing the first 500 points in the pseudo-random sequence? Specify your answer including one digit after the decimal point.
+
+# --hints--
+
+`convexHoles()` should return `104924`.
+
+```js
+assert.strictEqual(convexHoles(), 104924);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function convexHoles() {
+
+ return true;
+}
+
+convexHoles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-253-tidying-up.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-253-tidying-up.md
new file mode 100644
index 00000000000..3dbeca51b38
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-253-tidying-up.md
@@ -0,0 +1,69 @@
+---
+id: 5900f4691000cf542c50ff7c
+title: 'Problem 253: Tidying up'
+challengeType: 1
+forumTopicId: 301901
+dashedName: problem-253-tidying-up
+---
+
+# --description--
+
+A small child has a "number caterpillar" consisting of forty jigsaw pieces, each with one number on it, which, when connected together in a line, reveal the numbers 1 to 40 in order.
+
+Every night, the child's father has to pick up the pieces of the caterpillar that have been scattered across the play room. He picks up the pieces at random and places them in the correct order.
+
+As the caterpillar is built up in this way, it forms distinct segments that gradually merge together. The number of segments starts at zero (no pieces placed), generally increases up to about eleven or twelve, then tends to drop again before finishing at a single segment (all pieces placed).
+
+For example:
+
+| Piece Placed | Segments So Far |
+| ------------ | --------------- |
+| 12 | 1 |
+| 4 | 2 |
+| 29 | 3 |
+| 6 | 4 |
+| 34 | 5 |
+| 5 | 4 |
+| 35 | 4 |
+| … | … |
+
+Let $M$ be the maximum number of segments encountered during a random tidy-up of the caterpillar. For a caterpillar of ten pieces, the number of possibilities for each $M$ is
+
+| M | Possibilities |
+| - | ------------- |
+| 1 | 512 |
+| 2 | 250912 |
+| 3 | 1815264 |
+| 4 | 1418112 |
+| 5 | 144000 |
+
+so the most likely value of $M$ is 3 and the average value is $\frac{385\\,643}{113\\,400} = 3.400732$, rounded to six decimal places.
+
+The most likely value of $M$ for a forty-piece caterpillar is 11; but what is the average value of $M$? Give your answer rounded to six decimal places.
+
+# --hints--
+
+`tidyingUp()` should return `11.492847`.
+
+```js
+assert.strictEqual(tidyingUp(), 11.492847);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function tidyingUp() {
+
+ return true;
+}
+
+tidyingUp();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-254-sums-of-digit-factorials.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-254-sums-of-digit-factorials.md
new file mode 100644
index 00000000000..3d91777d0a4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-254-sums-of-digit-factorials.md
@@ -0,0 +1,48 @@
+---
+id: 5900f46b1000cf542c50ff7d
+title: 'Problem 254: Sums of Digit Factorials'
+challengeType: 1
+forumTopicId: 301902
+dashedName: problem-254-sums-of-digit-factorials
+---
+
+# --description--
+
+Define $f(n)$ as the sum of the factorials of the digits of $n$. For example, $f(342) = 3! + 4! + 2! = 32$.
+
+Define $sf(n)$ as the sum of the digits of $f(n)$. So $sf(342) = 3 + 2 = 5$.
+
+Define $g(i)$ to be the smallest positive integer $n$ such that $sf(n) = i$. Though $sf(342)$ is 5, $sf(25)$ is also 5, and it can be verified that $g(5)$ is 25.
+
+Define $sg(i)$ as the sum of the digits of $g(i)$. So $sg(5) = 2 + 5 = 7$.
+
+Further, it can be verified that $g(20)$ is 267 and $\sum sg(i)$ for $1 ≤ i ≤ 20$ is 156.
+
+What is $\sum sg(i)$ for $1 ≤ i ≤ 150$?
+
+# --hints--
+
+`sumsOfDigitFactorials()` should return `8184523820510`.
+
+```js
+assert.strictEqual(sumsOfDigitFactorials(), 8184523820510);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumsOfDigitFactorials() {
+
+ return true;
+}
+
+sumsOfDigitFactorials();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-255-rounded-square-roots.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-255-rounded-square-roots.md
new file mode 100644
index 00000000000..abfbcfe2047
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-255-rounded-square-roots.md
@@ -0,0 +1,67 @@
+---
+id: 5900f46d1000cf542c50ff7f
+title: 'Problem 255: Rounded Square Roots'
+challengeType: 1
+forumTopicId: 301903
+dashedName: problem-255-rounded-square-roots
+---
+
+# --description--
+
+We define the rounded-square-root of a positive integer $n$ as the square root of $n$ rounded to the nearest integer.
+
+The following procedure (essentially Heron's method adapted to integer arithmetic) finds the rounded-square-root of $n$:
+
+Let $d$ be the number of digits of the number $n$.
+
+If $d$ is odd, set $x_0 = 2 × {10}^{\frac{d - 1}{2}}$.
+
+If $d$ is even, set $x_0 = 7 × {10}^{\frac{d - 2}{2}}$.
+
+Repeat:
+
+$$x_{k + 1} = \left\lfloor\frac{x_k + \left\lceil\frac{n}{x_k}\right\rceil}{2}\right\rfloor$$
+
+until $x_{k + 1} = x_k$.
+
+As an example, let us find the rounded-square-root of $n = 4321$.
+
+$n$ has 4 digits, so $x_0 = 7 × {10}^{\frac{4-2}{2}} = 70$.
+
+$$x_1 = \left\lfloor\frac{70 + \left\lceil\frac{4321}{70}\right\rceil}{2}\right\rfloor = 66 \\\\
+x_2 = \left\lfloor\frac{66 + \left\lceil\frac{4321}{66}\right\rceil}{2}\right\rfloor = 66$$
+
+Since $x_2 = x_1$, we stop here. So, after just two iterations, we have found that the rounded-square-root of 4321 is 66 (the actual square root is 65.7343137…).
+
+The number of iterations required when using this method is surprisingly low. For example, we can find the rounded-square-root of a 5-digit integer ($10\\,000 ≤ n ≤ 99\\,999$) with an average of 3.2102888889 iterations (the average value was rounded to 10 decimal places).
+
+Using the procedure described above, what is the average number of iterations required to find the rounded-square-root of a 14-digit number (${10}^{13} ≤ n < {10}^{14}$)? Give your answer rounded to 10 decimal places.
+
+**Note:** The symbols $⌊x⌋$ and $⌈x⌉$ represent the floor function and ceiling function respectively.
+
+# --hints--
+
+`roundedSquareRoots()` should return `4.447401118`.
+
+```js
+assert.strictEqual(roundedSquareRoots(), 4.447401118);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function roundedSquareRoots() {
+
+ return true;
+}
+
+roundedSquareRoots();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-256-tatami-free-rooms.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-256-tatami-free-rooms.md
new file mode 100644
index 00000000000..170443188b8
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-256-tatami-free-rooms.md
@@ -0,0 +1,56 @@
+---
+id: 5900f46c1000cf542c50ff7e
+title: 'Problem 256: Tatami-Free Rooms'
+challengeType: 1
+forumTopicId: 301904
+dashedName: problem-256-tatami-free-rooms
+---
+
+# --description--
+
+Tatami are rectangular mats, used to completely cover the floor of a room, without overlap.
+
+Assuming that the only type of available tatami has dimensions 1×2, there are obviously some limitations for the shape and size of the rooms that can be covered.
+
+For this problem, we consider only rectangular rooms with integer dimensions $a$, $b$ and even size $s = a \times b$. We use the term 'size' to denote the floor surface area of the room, and — without loss of generality — we add the condition $a ≤ b$.
+
+There is one rule to follow when laying out tatami: there must be no points where corners of four different mats meet. For example, consider the two arrangements below for a 4×4 room:
+
+
+
+The arrangement on the left is acceptable, whereas the one on the right is not: a red "X" in the middle, marks the point where four tatami meet.
+
+Because of this rule, certain even-sized rooms cannot be covered with tatami: we call them tatami-free rooms. Further, we define $T(s)$ as the number of tatami-free rooms of size $s$.
+
+The smallest tatami-free room has size $s = 70$ and dimensions 7×10. All the other rooms of size $s = 70$ can be covered with tatami; they are: 1×70, 2×35 and 5×14. Hence, $T(70) = 1$.
+
+Similarly, we can verify that $T(1320) = 5$ because there are exactly 5 tatami-free rooms of size $s = 1320$: 20×66, 22×60, 24×55, 30×44 and 33×40. In fact, $s = 1320$ is the smallest room-size $s$ for which $T(s) = 5$.
+
+Find the smallest room-size $s$ for which $T(s) = 200$.
+
+# --hints--
+
+`tatamiFreeRooms()` should return `85765680`.
+
+```js
+assert.strictEqual(tatamiFreeRooms(), 85765680);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function tatamiFreeRooms() {
+
+ return true;
+}
+
+tatamiFreeRooms();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-257-angular-bisectors.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-257-angular-bisectors.md
new file mode 100644
index 00000000000..60864ac52e1
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-257-angular-bisectors.md
@@ -0,0 +1,46 @@
+---
+id: 5900f46e1000cf542c50ff80
+title: 'Problem 257: Angular Bisectors'
+challengeType: 1
+forumTopicId: 301905
+dashedName: problem-257-angular-bisectors
+---
+
+# --description--
+
+Given is an integer sided triangle $ABC$ with sides $a ≤ b ≤ c$ ($AB = c$, $BC = a$ and $AC = b$).
+
+The angular bisectors of the triangle intersect the sides at points $E$, $F$ and $G$ (see picture below).
+
+
+
+The segments $EF$, $EG$ and $FG$ partition the triangle $ABC$ into four smaller triangles: $AEG$, $BFE$, $CGF$ and $EFG$. It can be proven that for each of these four triangles the ratio $\frac{\text{area}(ABC)}{\text{area}(\text{subtriangle})}$ is rational. However, there exist triangles for which some or all of these ratios are integral.
+
+How many triangles $ABC$ with perimeter $≤ 100\\,000\\,000$ exist so that the ratio $\frac{\text{area}(ABC)}{\text{area}(AEG)}$ is integral?
+
+# --hints--
+
+`angularBisectors()` should return `139012411`.
+
+```js
+assert.strictEqual(angularBisectors(), 139012411);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function angularBisectors() {
+
+ return true;
+}
+
+angularBisectors();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-258-a-lagged-fibonacci-sequence.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-258-a-lagged-fibonacci-sequence.md
new file mode 100644
index 00000000000..d21eb673b78
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-258-a-lagged-fibonacci-sequence.md
@@ -0,0 +1,43 @@
+---
+id: 5900f46e1000cf542c50ff81
+title: 'Problem 258: A lagged Fibonacci sequence'
+challengeType: 1
+forumTopicId: 301906
+dashedName: problem-258-a-lagged-fibonacci-sequence
+---
+
+# --description--
+
+A sequence is defined as:
+
+- $g_k = 1$, for $0 ≤ k ≤ 1999$
+- $g_k = g_{k - 2000} + g_{k - 1999}$, for $k ≥ 2000$.
+
+Find $g_k$ mod 20092010 for $k = {10}^{18}$.
+
+# --hints--
+
+`laggedFibonacciSequence()` should return `12747994`.
+
+```js
+assert.strictEqual(laggedFibonacciSequence(), 12747994);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function laggedFibonacciSequence() {
+
+ return true;
+}
+
+laggedFibonacciSequence();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-259-reachable-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-259-reachable-numbers.md
new file mode 100644
index 00000000000..a8fa3ceb470
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-259-reachable-numbers.md
@@ -0,0 +1,49 @@
+---
+id: 5900f4701000cf542c50ff82
+title: 'Problem 259: Reachable Numbers'
+challengeType: 1
+forumTopicId: 301907
+dashedName: problem-259-reachable-numbers
+---
+
+# --description--
+
+A positive integer will be called reachable if it can result from an arithmetic expression obeying the following rules:
+
+- Uses the digits 1 through 9, in that order and exactly once each.
+- Any successive digits can be concatenated (for example, using the digits 2, 3 and 4 we obtain the number 234).
+- Only the four usual binary arithmetic operations (addition, subtraction, multiplication and division) are allowed.
+- Each operation can be used any number of times, or not at all.
+- Unary minus is not allowed.
+- Any number of (possibly nested) parentheses may be used to define the order of operations.
+
+For example, 42 is reachable, since $\frac{1}{23} \times ((4 \times 5) - 6) \times (78 - 9) = 42$.
+
+What is the sum of all positive reachable integers?
+
+# --hints--
+
+`reachableNumbers()` should return `20101196798`.
+
+```js
+assert.strictEqual(reachableNumbers(), 20101196798);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function reachableNumbers() {
+
+ return true;
+}
+
+reachableNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-260-stone-game.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-260-stone-game.md
new file mode 100644
index 00000000000..d0724fd1214
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-260-stone-game.md
@@ -0,0 +1,60 @@
+---
+id: 5900f4701000cf542c50ff83
+title: 'Problem 260: Stone Game'
+challengeType: 1
+forumTopicId: 301909
+dashedName: problem-260-stone-game
+---
+
+# --description--
+
+A game is played with three piles of stones and two players.
+
+On each player's turn, the player removes one or more stones from the piles. However, if the player takes stones from more than one pile, the same number of stones must be removed from each of the selected piles.
+
+In other words, the player chooses some $N > 0$ and removes:
+
+- $N$ stones from any single pile; or
+- $N$ stones from each of any two piles ($2N$ total); or
+- $N$ stones from each of the three piles ($3N$ total).
+
+The player taking the last stone(s) wins the game.
+
+A winning configuration is one where the first player can force a win.
+
+For example, (0,0,13), (0,11,11) and (5,5,5) are winning configurations because the first player can immediately remove all stones.
+
+A losing configuration is one where the second player can force a win, no matter what the first player does.
+
+For example, (0,1,2) and (1,3,3) are losing configurations: any legal move leaves a winning configuration for the second player.
+
+Consider all losing configurations ($x_i$,$y_i$,$z_i$) where $x_i ≤ y_i ≤ z_i ≤ 100$. We can verify that $\sum (x_i + y_i + z_i) = 173\\,895$ for these.
+
+Find $\sum (x_i + y_i + z_i)$ where ($x_i$,$y_i$,$z_i$) ranges over the losing configurations with $x_i ≤ y_i ≤ z_i ≤ 1000$.
+
+# --hints--
+
+`stoneGame()` should return `167542057`.
+
+```js
+assert.strictEqual(stoneGame(), 167542057);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function stoneGame() {
+
+ return true;
+}
+
+stoneGame();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-261-pivotal-square-sums.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-261-pivotal-square-sums.md
new file mode 100644
index 00000000000..af6e1b5aa27
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-261-pivotal-square-sums.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4711000cf542c50ff84
+title: 'Problem 261: Pivotal Square Sums'
+challengeType: 1
+forumTopicId: 301910
+dashedName: problem-261-pivotal-square-sums
+---
+
+# --description--
+
+Let us call a positive integer $k$ a square-pivot, if there is a pair of integers $m > 0$ and $n ≥ k$, such that the sum of the ($m + 1$) consecutive squares up to $k$ equals the sum of the $m$ consecutive squares from ($n + 1$) on:
+
+$${(k - m)}^2 + \ldots + k^2 = {(n + 1)}^2 + \ldots + {(n + m)}^2$$
+
+Some small square-pivots are
+
+$$\begin{align} & \mathbf{4}: 3^2 + \mathbf{4}^2 = 5^2 \\\\
+ & \mathbf{21}: {20}^2 + \mathbf{21}^2 = {29}^2 \\\\ & \mathbf{24}: {21}^2 + {22}^2 + {23}^2 + \mathbf{24}^2 = {25}^2 + {26}^2 + {27}^2 \\\\
+ & \mathbf{110}: {108}^2 + {109}^2 + \mathbf{110}^2 = {133}^2 + {134}^2 \\\\ \end{align}$$
+
+Find the sum of all distinct square-pivots $≤ {10}^{10}$.
+
+# --hints--
+
+`pivotalSquareSums()` should return `238890850232021`.
+
+```js
+assert.strictEqual(pivotalSquareSums(), 238890850232021);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pivotalSquareSums() {
+
+ return true;
+}
+
+pivotalSquareSums();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-262-mountain-range.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-262-mountain-range.md
new file mode 100644
index 00000000000..d340e834fa6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-262-mountain-range.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4731000cf542c50ff85
+title: 'Problem 262: Mountain Range'
+challengeType: 1
+forumTopicId: 301911
+dashedName: problem-262-mountain-range
+---
+
+# --description--
+
+The following equation represents the continuous topography of a mountainous region, giving the elevation $h$ at any point ($x$,$y$):
+
+$$h = \left(5000 - \frac{x^2 + y^2 + xy}{200} + \frac{25(x + y)}{2}\right) \times e^{-\left|\frac{x^2 + y^2}{1\\,000\\,000} - \frac{3(x + y)}{2000} + \frac{7}{10}\right|}$$
+
+A mosquito intends to fly from A(200,200) to B(1400,1400), without leaving the area given by $0 ≤ x$, $y ≤ 1600$.
+
+Because of the intervening mountains, it first rises straight up to a point A', having elevation $f$. Then, while remaining at the same elevation $f$, it flies around any obstacles until it arrives at a point B' directly above B.
+
+First, determine $f_{min}$ which is the minimum constant elevation allowing such a trip from A to B, while remaining in the specified area. Then, find the length of the shortest path between A' and B', while flying at that constant elevation $f_{min}$.
+
+Give that length as your answer, rounded to three decimal places.
+
+**Note:** For convenience, the elevation function shown above is repeated below, in a form suitable for most programming languages: `h=( 5000-0.005*(x*x+y*y+x*y)+12.5*(x+y) )* exp( -abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7) )`.
+
+# --hints--
+
+`mountainRange()` should return `2531.205`.
+
+```js
+assert.strictEqual(mountainRange(), 2531.205);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function mountainRange() {
+
+ return true;
+}
+
+mountainRange();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-263-an-engineers-dream-come-true.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-263-an-engineers-dream-come-true.md
new file mode 100644
index 00000000000..8fec64cc250
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-263-an-engineers-dream-come-true.md
@@ -0,0 +1,57 @@
+---
+id: 5900f4741000cf542c50ff86
+title: 'Problem 263: An engineers'' dream come true'
+challengeType: 1
+forumTopicId: 301912
+dashedName: problem-263-an-engineers-dream-come-true
+---
+
+# --description--
+
+Consider the number 6. The divisors of 6 are: 1,2,3 and 6.
+
+Every number from 1 up to and including 6 can be written as a sum of distinct divisors of 6:
+
+$1 = 1$, $2 = 2$, $3 = 1 + 2$, $4 = 1 + 3$, $5 = 2 + 3$, $6 = 6$.
+
+A number $n$ is called a practical number if every number from 1 up to and including $n$ can be expressed as a sum of distinct divisors of $n$.
+
+A pair of consecutive prime numbers with a difference of six is called a sexy pair (since "sex" is the Latin word for "six"). The first sexy pair is (23, 29).
+
+We may occasionally find a triple-pair, which means three consecutive sexy prime pairs, such that the second member of each pair is the first member of the next pair.
+
+We shall call a number $n$ such that:
+
+- ($n - 9$, $n - 3$), ($n - 3$, $n + 3$), ($n + 3$, $n + 9$) form a triple-pair, and
+- the numbers $n - 8$, $n - 4$, $n$, $n + 4$ and $n + 8$ are all practical,
+
+an engineers’ paradise.
+
+Find the sum of the first four engineers’ paradises.
+
+# --hints--
+
+`engineersDreamComeTrue()` should return `2039506520`.
+
+```js
+assert.strictEqual(engineersDreamComeTrue(), 2039506520);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function engineersDreamComeTrue() {
+
+ return true;
+}
+
+engineersDreamComeTrue();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-264-triangle-centres.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-264-triangle-centres.md
new file mode 100644
index 00000000000..dc22c0cf51b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-264-triangle-centres.md
@@ -0,0 +1,71 @@
+---
+id: 5900f4751000cf542c50ff87
+title: 'Problem 264: Triangle Centres'
+challengeType: 1
+forumTopicId: 301913
+dashedName: problem-264-triangle-centres
+---
+
+# --description--
+
+Consider all the triangles having:
+
+- All their vertices on lattice points.
+- Circumcentre at the origin O.
+- Orthocentre at the point H(5, 0).
+
+There are nine such triangles having a $\text{perimeter} ≤ 50$.
+
+Listed and shown in ascending order of their perimeter, they are:
+
+|
+A(-4, 3), B(5, 0), C(4, -3) +A(4, 3), B(5, 0), C(-4, -3) +A(-3, 4), B(5, 0), C(3, -4) + +A(3, 4), B(5, 0), C(-3, -4) +A(0, 5), B(5, 0), C(0, -5) +A(1, 8), B(8, -1), C(-4, -7) + +A(8, 1), B(1, -8), C(-4, 7) +A(2, 9), B(9, -2), C(-6, -7) +A(9, 2), B(2, -9), C(-6, 7) + |
+  |
+
+
+For the first arrangement, the 3-digit subsequences, in clockwise order, are: 000, 001, 010, 101, 011, 111, 110 and 100.
+
+Each circular arrangement can be encoded as a number by concatenating the binary digits starting with the subsequence of all zeros as the most significant bits and proceeding clockwise. The two arrangements for $N = 3$ are thus represented as 23 and 29:
+
+$${00010111}_2 = 23\\\\
+{00011101}_2 = 29$$
+
+Calling $S(N)$ the sum of the unique numeric representations, we can see that $S(3) = 23 + 29 = 52$.
+
+Find $S(5)$.
+
+# --hints--
+
+`binaryCircles()` should return `209110240768`.
+
+```js
+assert.strictEqual(binaryCircles(), 209110240768);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function binaryCircles() {
+
+ return true;
+}
+
+binaryCircles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-266-pseudo-square-root.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-266-pseudo-square-root.md
new file mode 100644
index 00000000000..2b22e967efb
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-266-pseudo-square-root.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4771000cf542c50ff89
+title: 'Problem 266: Pseudo Square Root'
+challengeType: 1
+forumTopicId: 301915
+dashedName: problem-266-pseudo-square-root
+---
+
+# --description--
+
+The divisors of 12 are: 1,2,3,4,6 and 12.
+
+The largest divisor of 12 that does not exceed the square root of 12 is 3.
+
+We shall call the largest divisor of an integer $n$ that does not exceed the square root of $n$ the pseudo square root ($PSR$) of $n$.
+
+It can be seen that $PSR(3102) = 47$.
+
+Let $p$ be the product of the primes below 190. Find $PSR(p)\bmod {10}^{16}$.
+
+# --hints--
+
+`pseudoSquareRoot()` should return `1096883702440585`.
+
+```js
+assert.strictEqual(pseudoSquareRoot(), 1096883702440585);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pseudoSquareRoot() {
+
+ return true;
+}
+
+pseudoSquareRoot();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-267-billionaire.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-267-billionaire.md
new file mode 100644
index 00000000000..8dbe1d8ab66
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-267-billionaire.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4771000cf542c50ff8a
+title: 'Problem 267: Billionaire'
+challengeType: 1
+forumTopicId: 301916
+dashedName: problem-267-billionaire
+---
+
+# --description--
+
+You are given a unique investment opportunity.
+
+Starting with £1 of capital, you can choose a fixed proportion, $f$, of your capital to bet on a fair coin toss repeatedly for 1000 tosses.
+
+Your return is double your bet for heads and you lose your bet for tails.
+
+For example, if $f = \frac{1}{4}$, for the first toss you bet £0.25, and if heads comes up you win £0.5 and so then have £1.5. You then bet £0.375 and if the second toss is tails, you have £1.125.
+
+Choosing $f$ to maximize your chances of having at least £1,000,000,000 after 1,000 flips, what is the chance that you become a billionaire?
+
+All computations are assumed to be exact (no rounding), but give your answer rounded to 12 digits behind the decimal point in the form 0.abcdefghijkl.
+
+# --hints--
+
+`billionaire()` should return `0.999992836187`.
+
+```js
+assert.strictEqual(billionaire(), 0.999992836187);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function billionaire() {
+
+ return true;
+}
+
+billionaire();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md
new file mode 100644
index 00000000000..bd295d89e67
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4791000cf542c50ff8b
+title: >-
+ Problem 268: Counting numbers with at least four distinct prime factors less than 100
+challengeType: 1
+forumTopicId: 301917
+dashedName: >-
+ problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100
+---
+
+# --description--
+
+It can be verified that there are 23 positive integers less than 1000 that are divisible by at least four distinct primes less than 100.
+
+Find how many positive integers less than ${10}^{16}$ are divisible by at least four distinct primes less than 100.
+
+# --hints--
+
+`fourDistinctPrimeFactors()` should return `785478606870985`.
+
+```js
+assert.strictEqual(fourDistinctPrimeFactors(), 785478606870985);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function fourDistinctPrimeFactors() {
+
+ return true;
+}
+
+fourDistinctPrimeFactors();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-269-polynomials-with-at-least-one-integer-root.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-269-polynomials-with-at-least-one-integer-root.md
new file mode 100644
index 00000000000..3b66b2a2ab1
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-269-polynomials-with-at-least-one-integer-root.md
@@ -0,0 +1,54 @@
+---
+id: 5900f4791000cf542c50ff8c
+title: 'Problem 269: Polynomials with at least one integer root'
+challengeType: 1
+forumTopicId: 301918
+dashedName: problem-269-polynomials-with-at-least-one-integer-root
+---
+
+# --description--
+
+A root or zero of a polynomial $P(x)$ is a solution to the equation $P(x) = 0$.
+
+Define $P_n$ as the polynomial whose coefficients are the digits of $n$.
+
+For example, $P_{5703}(x) = 5x^3 + 7x^2 + 3$.
+
+We can see that:
+
+- $P_n(0)$ is the last digit of $n$,
+- $P_n(1)$ is the sum of the digits of $n$,
+- $Pn(10)$ is $n$ itself.
+
+Define $Z(k)$ as the number of positive integers, $n$, not exceeding $k$ for which the polynomial $P_n$ has at least one integer root.
+
+It can be verified that $Z(100\\,000)$ is 14696.
+
+What is $Z({10}^{16})$?
+
+# --hints--
+
+`polynomialsWithOneIntegerRoot()` should return `1311109198529286`.
+
+```js
+assert.strictEqual(polynomialsWithOneIntegerRoot(), 1311109198529286);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function polynomialsWithOneIntegerRoot() {
+
+ return true;
+}
+
+polynomialsWithOneIntegerRoot();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-270-cutting-squares.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-270-cutting-squares.md
new file mode 100644
index 00000000000..0458e257f05
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-270-cutting-squares.md
@@ -0,0 +1,48 @@
+---
+id: 5900f47c1000cf542c50ff8e
+title: 'Problem 270: Cutting Squares'
+challengeType: 1
+forumTopicId: 301920
+dashedName: problem-270-cutting-squares
+---
+
+# --description--
+
+A square piece of paper with integer dimensions $N×N$ is placed with a corner at the origin and two of its sides along the $x$- and $y$-axes. Then, we cut it up respecting the following rules:
+
+- We only make straight cuts between two points lying on different sides of the square, and having integer coordinates.
+- Two cuts cannot cross, but several cuts can meet at the same border point.
+- Proceed until no more legal cuts can be made.
+
+Counting any reflections or rotations as distinct, we call $C(N)$ the number of ways to cut an $N×N$ square. For example, $C(1) = 2$ and $C(2) = 30$ (shown below).
+
+
+
+What is $C(30)\bmod {10}^8$ ?
+
+# --hints--
+
+`cuttingSquares()` should return `82282080`.
+
+```js
+assert.strictEqual(cuttingSquares(), 82282080);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function cuttingSquares() {
+
+ return true;
+}
+
+cuttingSquares();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-271-modular-cubes-part-1.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-271-modular-cubes-part-1.md
new file mode 100644
index 00000000000..f1dbf4b5666
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-271-modular-cubes-part-1.md
@@ -0,0 +1,42 @@
+---
+id: 5900f47b1000cf542c50ff8d
+title: 'Problem 271: Modular Cubes, part 1'
+challengeType: 1
+forumTopicId: 301921
+dashedName: problem-271-modular-cubes-part-1
+---
+
+# --description--
+
+For a positive number $n$, define $S(n)$ as the sum of the integers $x$, for which $1 < x < n$ and $x^3 \equiv 1\bmod n$.
+
+When $n = 91$, there are 8 possible values for $x$, namely: 9, 16, 22, 29, 53, 74, 79, 81. Thus, $S(91) = 9 + 16 + 22 + 29 + 53 + 74 + 79 + 81 = 363$.
+
+Find $S(13\\,082\\,761\\,331\\,670\\,030)$.
+
+# --hints--
+
+`modularCubesOne()` should return `4617456485273130000`.
+
+```js
+assert.strictEqual(modularCubesOne(), 4617456485273130000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function modularCubesOne() {
+
+ return true;
+}
+
+modularCubesOne();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-272-modular-cubes-part-2.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-272-modular-cubes-part-2.md
new file mode 100644
index 00000000000..d764ea6563b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-272-modular-cubes-part-2.md
@@ -0,0 +1,42 @@
+---
+id: 5900f47d1000cf542c50ff8f
+title: 'Problem 272: Modular Cubes, part 2'
+challengeType: 1
+forumTopicId: 301922
+dashedName: problem-272-modular-cubes-part-2
+---
+
+# --description--
+
+For a positive number $n$, define $C(n)$ as the number of the integers $x$, for which $1 < x < n$ and $x^3 \equiv 1\bmod n$.
+
+When $n = 91$, there are 8 possible values for $x$, namely: 9, 16, 22, 29, 53, 74, 79, 81. Thus, $C(91) = 8$.
+
+Find the sum of the positive numbers $n ≤ {10}^{11}$ for which $C(n)=242$.
+
+# --hints--
+
+`modularCubesTwo()` should return `8495585919506151000`.
+
+```js
+assert.strictEqual(modularCubesTwo(), 8495585919506151000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function modularCubesTwo() {
+
+ return true;
+}
+
+modularCubesTwo();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-273-sum-of-squares.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-273-sum-of-squares.md
new file mode 100644
index 00000000000..d5ffc27c633
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-273-sum-of-squares.md
@@ -0,0 +1,48 @@
+---
+id: 5900f47e1000cf542c50ff90
+title: 'Problem 273: Sum of Squares'
+challengeType: 1
+forumTopicId: 301923
+dashedName: problem-273-sum-of-squares
+---
+
+# --description--
+
+Consider equations of the form: $a^2 + b^2 = N$, $0 ≤ a ≤ b$, $a$, $b$ and $N$ integer.
+
+For $N = 65$ there are two solutions:
+
+$a = 1, b = 8$ and $a = 4, b = 7$.
+
+We call $S(N)$ the sum of the values of $a$ of all solutions of $a^2 + b^2 = N$, $0 ≤ a ≤ b$, $a$, $b$ and $N$ integer.
+
+Thus $S(65) = 1 + 4 = 5$.
+
+Find $\sum S(N)$, for all squarefree $N$ only divisible by primes of the form $4k + 1$ with $4k + 1 < 150$.
+
+# --hints--
+
+`sumOfSquares()` should return `2032447591196869000`.
+
+```js
+assert.strictEqual(sumOfSquares(), 2032447591196869000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumOfSquares() {
+
+ return true;
+}
+
+sumOfSquares();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-274-divisibility-multipliers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-274-divisibility-multipliers.md
new file mode 100644
index 00000000000..bf56b697151
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-274-divisibility-multipliers.md
@@ -0,0 +1,52 @@
+---
+id: 5900f47f1000cf542c50ff91
+title: 'Problem 274: Divisibility Multipliers'
+challengeType: 1
+forumTopicId: 301924
+dashedName: problem-274-divisibility-multipliers
+---
+
+# --description--
+
+For each integer $p > 1$ coprime to 10 there is a positive divisibility multiplier $m < p$ which preserves divisibility by $p$ for the following function on any positive integer, $n$:
+
+$f(n) = (\text{all but the last digit of} \\; n) + (\text{the last digit of} \\; n) \times m$
+
+That is, if $m$ is the divisibility multiplier for $p$, then $f(n)$ is divisible by $p$ if and only if $n$ is divisible by $p$.
+
+(When $n$ is much larger than $p$, $f(n)$ will be less than $n$ and repeated application of $f$ provides a multiplicative divisibility test for $p$.)
+
+For example, the divisibility multiplier for 113 is 34.
+
+$f(76275) = 7627 + 5 \times 34 = 7797$: 76275 and 7797 are both divisible by 113
+
+$f(12345) = 1234 + 5 \times 34 = 1404$: 12345 and 1404 are both not divisible by 113
+
+The sum of the divisibility multipliers for the primes that are coprime to 10 and less than 1000 is 39517. What is the sum of the divisibility multipliers for the primes that are coprime to 10 and less than ${10}^7$?
+
+# --hints--
+
+`divisibilityMultipliers()` should return `1601912348822`.
+
+```js
+assert.strictEqual(divisibilityMultipliers(), 1601912348822);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function divisibilityMultipliers() {
+
+ return true;
+}
+
+divisibilityMultipliers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-275-balanced-sculptures.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-275-balanced-sculptures.md
new file mode 100644
index 00000000000..decc755a9ee
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-275-balanced-sculptures.md
@@ -0,0 +1,51 @@
+---
+id: 5900f4801000cf542c50ff92
+title: 'Problem 275: Balanced Sculptures'
+challengeType: 1
+forumTopicId: 301925
+dashedName: problem-275-balanced-sculptures
+---
+
+# --description--
+
+Let us define a balanced sculpture of order $n$ as follows:
+
+- A polyomino made up of $n + 1$ tiles known as the blocks ($n$ tiles) and the plinth (remaining tile);
+- the plinth has its centre at position ($x = 0$, $y = 0$);
+- the blocks have $y$-coordinates greater than zero (so the plinth is the unique lowest tile);
+- the centre of mass of all the blocks, combined, has $x$-coordinate equal to zero.
+
+When counting the sculptures, any arrangements which are simply reflections about the $y$-axis, are not counted as distinct. For example, the 18 balanced sculptures of order 6 are shown below; note that each pair of mirror images (about the $y$-axis) is counted as one sculpture:
+
+
+
+There are 964 balanced sculptures of order 10 and 360505 of order 15.
+
+How many balanced sculptures are there of order 18?
+
+# --hints--
+
+`balancedSculptures()` should return `15030564`.
+
+```js
+assert.strictEqual(balancedSculptures(), 15030564);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function balancedSculptures() {
+
+ return true;
+}
+
+balancedSculptures();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-276-primitive-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-276-primitive-triangles.md
new file mode 100644
index 00000000000..26ce00839b4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-276-primitive-triangles.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4801000cf542c50ff93
+title: 'Problem 276: Primitive Triangles'
+challengeType: 1
+forumTopicId: 301926
+dashedName: problem-276-primitive-triangles
+---
+
+# --description--
+
+Consider the triangles with integer sides $a$, $b$ and $c$ with $a ≤ b ≤ c$.
+
+An integer sided triangle $(a,b,c)$ is called primitive if $gcd(a,b,c) = 1$.
+
+How many primitive integer sided triangles exist with a perimeter not exceeding $10\\,000\\,000$?
+
+# --hints--
+
+`primitiveTriangles()` should return `5777137137739633000`.
+
+```js
+assert.strictEqual(primitiveTriangles(), 5777137137739633000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primitiveTriangles() {
+
+ return true;
+}
+
+primitiveTriangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-277-a-modified-collatz-sequence.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-277-a-modified-collatz-sequence.md
new file mode 100644
index 00000000000..c80635aa3d8
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-277-a-modified-collatz-sequence.md
@@ -0,0 +1,56 @@
+---
+id: 5900f4811000cf542c50ff94
+title: 'Problem 277: A Modified Collatz sequence'
+challengeType: 1
+forumTopicId: 301927
+dashedName: problem-277-a-modified-collatz-sequence
+---
+
+# --description--
+
+A modified Collatz sequence of integers is obtained from a starting value $a_1$ in the following way:
+
+$a_{n + 1} = \frac{a_n}{3}$ if $a_n$ is divisible by 3. We shall denote this as a large downward step, "D".
+
+$a_{n + 1} = \frac{4a_n + 2}{3}$ if $a_n$ divided by 3 gives a remainder of 1. We shall denote this as an upward step, "U".
+
+$a_{n + 1} = \frac{2a_n - 1}{3}$ if $a_n$ divided by 3 gives a remainder of 2. We shall denote this as a small downward step, "d".
+
+The sequence terminates when some $a_n = 1$.
+
+Given any integer, we can list out the sequence of steps. For instance if $a_1 = 231$, then the sequence $\\{a_n\\} = \\{231, 77, 51, 17, 11, 7, 10, 14, 9, 3, 1\\}$ corresponds to the steps "DdDddUUdDD".
+
+Of course, there are other sequences that begin with that same sequence "DdDddUUdDD....".
+
+For instance, if $a_1 = 1004064$, then the sequence is DdDddUUdDDDdUDUUUdDdUUDDDUdDD.
+
+In fact, 1004064 is the smallest possible $a_1 > {10}^6$ that begins with the sequence DdDddUUdDD.
+
+What is the smallest $a_1 > {10}^{15}$ that begins with the sequence "UDDDUdddDDUDDddDdDddDDUDDdUUDd"?
+
+# --hints--
+
+`modifiedCollatzSequence()` should return `1125977393124310`.
+
+```js
+assert.strictEqual(modifiedCollatzSequence(), 1125977393124310);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function modifiedCollatzSequence() {
+
+ return true;
+}
+
+modifiedCollatzSequence();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-278-linear-combinations-of-semiprimes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-278-linear-combinations-of-semiprimes.md
new file mode 100644
index 00000000000..215c51cb036
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-278-linear-combinations-of-semiprimes.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4831000cf542c50ff95
+title: 'Problem 278: Linear Combinations of Semiprimes'
+challengeType: 1
+forumTopicId: 301928
+dashedName: problem-278-linear-combinations-of-semiprimes
+---
+
+# --description--
+
+Given the values of integers $1 < a_1 < a_2 < \ldots < a_n$, consider the linear combination $q_1a_1 + q_2a_2 + \ldots + q_na_n = b$, using only integer values $q_k ≥ 0$.
+
+Note that for a given set of $a_k$, it may be that not all values of $b$ are possible. For instance, if $a_1 = 5$ and $a_2 = 7$, there are no $q_1 ≥ 0$ and $q_2 ≥ 0$ such that $b$ could be 1, 2, 3, 4, 6, 8, 9, 11, 13, 16, 18 or 23.
+
+In fact, 23 is the largest impossible value of $b$ for $a_1 = 5$ and $a_2 = 7$. We therefore call $f(5, 7) = 23$. Similarly, it can be shown that $f(6, 10, 15)=29$ and $f(14, 22, 77) = 195$.
+
+Find $\sum f(pq,pr,qr)$, where $p$, $q$ and $r$ are prime numbers and $p < q < r < 5000$.
+
+# --hints--
+
+`linearCombinationOfSemiprimes()` should return `1228215747273908500`.
+
+```js
+assert.strictEqual(linearCombinationOfSemiprimes(), 1228215747273908500);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function linearCombinationOfSemiprimes() {
+
+ return true;
+}
+
+linearCombinationOfSemiprimes();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-279-triangles-with-integral-sides-and-an-integral-angle.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-279-triangles-with-integral-sides-and-an-integral-angle.md
new file mode 100644
index 00000000000..9d50a5ebc61
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-279-triangles-with-integral-sides-and-an-integral-angle.md
@@ -0,0 +1,38 @@
+---
+id: 5900f4841000cf542c50ff96
+title: 'Problem 279: Triangles with integral sides and an integral angle'
+challengeType: 1
+forumTopicId: 301929
+dashedName: problem-279-triangles-with-integral-sides-and-an-integral-angle
+---
+
+# --description--
+
+How many triangles are there with integral sides, at least one integral angle (measured in degrees), and a perimeter that does not exceed ${10}^8$?
+
+# --hints--
+
+`trianglesWithIntegralSidesAndAngle()` should return `416577688`.
+
+```js
+assert.strictEqual(trianglesWithIntegralSidesAndAngle(), 416577688);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function trianglesWithIntegralSidesAndAngle() {
+
+ return true;
+}
+
+trianglesWithIntegralSidesAndAngle();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-280-ant-and-seeds.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-280-ant-and-seeds.md
new file mode 100644
index 00000000000..5057b8bd47c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-280-ant-and-seeds.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4841000cf542c50ff97
+title: 'Problem 280: Ant and seeds'
+challengeType: 1
+forumTopicId: 301931
+dashedName: problem-280-ant-and-seeds
+---
+
+# --description--
+
+A laborious ant walks randomly on a 5x5 grid. The walk starts from the central square. At each step, the ant moves to an adjacent square at random, without leaving the grid; thus there are 2, 3 or 4 possible moves at each step depending on the ant's position.
+
+At the start of the walk, a seed is placed on each square of the lower row. When the ant isn't carrying a seed and reaches a square of the lower row containing a seed, it will start to carry the seed. The ant will drop the seed on the first empty square of the upper row it eventually reaches.
+
+What's the expected number of steps until all seeds have been dropped in the top row? Give your answer rounded to 6 decimal places.
+
+# --hints--
+
+`antAndSeeds()` should return `430.088247`.
+
+```js
+assert.strictEqual(antAndSeeds(), 430.088247);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function antAndSeeds() {
+
+ return true;
+}
+
+antAndSeeds();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-281-pizza-toppings.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-281-pizza-toppings.md
new file mode 100644
index 00000000000..60b84a893f8
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-281-pizza-toppings.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4861000cf542c50ff98
+title: 'Problem 281: Pizza Toppings'
+challengeType: 1
+forumTopicId: 301932
+dashedName: problem-281-pizza-toppings
+---
+
+# --description--
+
+You are given a pizza (perfect circle) that has been cut into $m·n$ equal pieces and you want to have exactly one topping on each slice.
+
+Let $f(m,n)$ denote the number of ways you can have toppings on the pizza with $m$ different toppings ($m ≥ 2$), using each topping on exactly $n$ slices ($n ≥ 1$). Reflections are considered distinct, rotations are not.
+
+Thus, for instance, $f(2,1) = 1$, $f(2,2) = f(3,1) = 2$ and $f(3,2) = 16$. $f(3,2)$ is shown below:
+
+
+
+Find the sum of all $f(m,n)$ such that $f(m,n) ≤ {10}^{15}$.
+
+# --hints--
+
+`pizzaToppings()` should return `1485776387445623`.
+
+```js
+assert.strictEqual(pizzaToppings(), 1485776387445623);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pizzaToppings() {
+
+ return true;
+}
+
+pizzaToppings();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-282-the-ackermann-function.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-282-the-ackermann-function.md
new file mode 100644
index 00000000000..c9cbb75087d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-282-the-ackermann-function.md
@@ -0,0 +1,45 @@
+---
+id: 5900f4861000cf542c50ff99
+title: 'Problem 282: The Ackermann function'
+challengeType: 1
+forumTopicId: 301933
+dashedName: problem-282-the-ackermann-function
+---
+
+# --description--
+
+For non-negative integers $m$, $n$, the Ackermann function $A(m, n)$ is defined as follows:
+
+$$A(m, n) = \begin{cases} n + 1 & \text{if $m = 0$} \\\\
+A(m - 1, 1) & \text{if $m > 0$ and $n = 0$} \\\\ A(m - 1, A(m, n - 1)) & \text{if $m > 0$ and $n > 0$} \end{cases}$$
+
+For example $A(1, 0) = 2$, $A(2, 2) = 7$ and $A(3, 4) = 125$.
+
+Find $\displaystyle\sum_{n = 0}^6 A(n, n)$ and give your answer mod ${14}^8$.
+
+# --hints--
+
+`ackermanFunction()` should return `1098988351`.
+
+```js
+assert.strictEqual(ackermanFunction(), 1098988351);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function ackermanFunction() {
+
+ return true;
+}
+
+ackermanFunction();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
new file mode 100644
index 00000000000..e32d0d74b9d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4881000cf542c50ff9a
+title: >-
+ Problem 283: Integer sided triangles for which the area / perimeter ratio is integral
+challengeType: 1
+forumTopicId: 301934
+dashedName: >-
+ problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral
+---
+
+# --description--
+
+Consider the triangle with sides 6, 8 and 10. It can be seen that the perimeter and the area are both equal to 24.
+
+So the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 1.
+
+Consider also the triangle with sides 13, 14 and 15. The perimeter equals 42 while the area is equal to 84.
+
+So for this triangle the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 2.
+
+Find the sum of the perimeters of all integer sided triangles for which the area/perimeter ratios are equal to positive integers not exceeding 1000.
+
+# --hints--
+
+`integralAreaPerimeterRatio()` should return `28038042525570324`.
+
+```js
+assert.strictEqual(integralAreaPerimeterRatio(), 28038042525570324);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function integralAreaPerimeterRatio() {
+
+ return true;
+}
+
+integralAreaPerimeterRatio();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-284-steady-squares.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-284-steady-squares.md
new file mode 100644
index 00000000000..d6c86b00055
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-284-steady-squares.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4891000cf542c50ff9b
+title: 'Problem 284: Steady Squares'
+challengeType: 1
+forumTopicId: 301935
+dashedName: problem-284-steady-squares
+---
+
+# --description--
+
+The 3-digit number 376 in the decimal numbering system is an example of numbers with the special property that its square ends with the same digits: ${376}^2 = 141376$. Let's call a number with this property a steady square.
+
+Steady squares can also be observed in other numbering systems. In the base 14 numbering system, the 3-digit number $c37$ is also a steady square: $c37^2 = aa0c37$, and the sum of its digits is $c+3+7=18$ in the same numbering system. The letters $a$, $b$, $c$ and $d$ are used for the 10, 11, 12 and 13 digits respectively, in a manner similar to the hexadecimal numbering system.
+
+For $1 ≤ n ≤ 9$, the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system is $2d8$ (582 decimal). Steady squares with leading 0's are not allowed.
+
+Find the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system for $1 ≤ n ≤ 10000$ (decimal) and give your answer as a string in the base 14 system using lower case letters where necessary.
+
+# --hints--
+
+`steadySquares()` should return a string.
+
+```js
+assert(typeof steadySquares() === 'string');
+```
+
+`steadySquares()` should return the string `5a411d7b`.
+
+```js
+assert.strictEqual(steadySquares(), '5a411d7b');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function steadySquares() {
+
+ return true;
+}
+
+steadySquares();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-285-pythagorean-odds.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-285-pythagorean-odds.md
new file mode 100644
index 00000000000..5c6e49167f9
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-285-pythagorean-odds.md
@@ -0,0 +1,46 @@
+---
+id: 5900f48a1000cf542c50ff9c
+title: 'Problem 285: Pythagorean odds'
+challengeType: 1
+forumTopicId: 301936
+dashedName: problem-285-pythagorean-odds
+---
+
+# --description--
+
+Albert chooses a positive integer $k$, then two real numbers $a$, $b$ are randomly chosen in the interval [0,1] with uniform distribution.
+
+The square root of the sum ${(ka + 1)}^2 + {(kb + 1)}^2$ is then computed and rounded to the nearest integer. If the result is equal to $k$, he scores $k$ points; otherwise he scores nothing.
+
+For example, if $k = 6$, $a = 0.2$ and $b = 0.85$, then ${(ka + 1)}^2 + {(kb + 1)}^2 = 42.05$. The square root of 42.05 is 6.484... and when rounded to the nearest integer, it becomes 6. This is equal to $k$, so he scores 6 points.
+
+It can be shown that if he plays 10 turns with $k = 1, k = 2, \ldots, k = 10$, the expected value of his total score, rounded to five decimal places, is 10.20914.
+
+If he plays ${10}^5$ turns with $k = 1, k = 2, k = 3, \ldots, k = {10}^5$, what is the expected value of his total score, rounded to five decimal places?
+
+# --hints--
+
+`pythagoreanOdds()` should return `157055.80999`.
+
+```js
+assert.strictEqual(pythagoreanOdds(), 157055.80999);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pythagoreanOdds() {
+
+ return true;
+}
+
+pythagoreanOdds();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-286-scoring-probabilities.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-286-scoring-probabilities.md
new file mode 100644
index 00000000000..26e3e198604
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-286-scoring-probabilities.md
@@ -0,0 +1,42 @@
+---
+id: 5900f48a1000cf542c50ff9d
+title: 'Problem 286: Scoring probabilities'
+challengeType: 1
+forumTopicId: 301937
+dashedName: problem-286-scoring-probabilities
+---
+
+# --description--
+
+Barbara is a mathematician and a basketball player. She has found that the probability of scoring a point when shooting from a distance $x$ is exactly ($1 - \frac{x}{q}$), where $q$ is a real constant greater than 50.
+
+During each practice run, she takes shots from distances $x = 1, x = 2, \ldots, x = 50$ and, according to her records, she has precisely a 2 % chance to score a total of exactly 20 points.
+
+Find $q$ and give your answer rounded to 10 decimal places.
+
+# --hints--
+
+`scoringProbabilities()` should return `52.6494571953`.
+
+```js
+assert.strictEqual(scoringProbabilities(), 52.6494571953);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function scoringProbabilities() {
+
+ return true;
+}
+
+scoringProbabilities();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-287-quadtree-encoding-a-simple-compression-algorithm.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
new file mode 100644
index 00000000000..707a6fa97e7
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
@@ -0,0 +1,59 @@
+---
+id: 5900f48b1000cf542c50ff9e
+title: 'Problem 287: Quadtree encoding (a simple compression algorithm)'
+challengeType: 1
+forumTopicId: 301938
+dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
+---
+
+# --description--
+
+The quadtree encoding allows us to describe a $2^N×2^N$ black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
+
+- the first bit deals with the complete $2^N×2^N$ region;
+- "0" denotes a split:
+ - the current $2^n×2^n$ region is divided into 4 sub-regions of dimension $2^{n - 1}×2^{n - 1}$,
+ - the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
+- "10" indicates that the current region contains only black pixels;
+- "11" indicates that the current region contains only white pixels.
+
+Consider the following 4×4 image (colored marks denote places where a split can occur):
+
+
+
+This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
+
+For a positive integer $N$, define $D_N$ as the $2^N×2^N$ image with the following coloring scheme:
+
+- the pixel with coordinates $x = 0$, $y = 0$ corresponds to the bottom left pixel,
+- if ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ then the pixel is black,
+- otherwise the pixel is white.
+
+What is the length of the minimal sequence describing $D_{24}$?
+
+# --hints--
+
+`quadtreeEncoding()` should return `313135496`.
+
+```js
+assert.strictEqual(quadtreeEncoding(), 313135496);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function quadtreeEncoding() {
+
+ return true;
+}
+
+quadtreeEncoding();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-288-an-enormous-factorial.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-288-an-enormous-factorial.md
new file mode 100644
index 00000000000..cd92a15cd8c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-288-an-enormous-factorial.md
@@ -0,0 +1,49 @@
+---
+id: 5900f48d1000cf542c50ff9f
+title: 'Problem 288: An enormous factorial'
+challengeType: 1
+forumTopicId: 301939
+dashedName: problem-288-an-enormous-factorial
+---
+
+# --description--
+
+For any prime $p$ the number $N(p,q)$ is defined by $N(p,q) = \sum_{n=0}^q T_n \times p^n$ with $T_n$ generated by the following random number generator:
+
+$$\begin{align} & S_0 = 290797 \\\\
+ & S_{n + 1} = {S_n}^2\bmod 50\\,515\\,093 \\\\ & T_n = S_n\bmod p \end{align}$$
+
+Let $Nfac(p,q)$ be the factorial of $N(p,q)$.
+
+Let $NF(p,q)$ be the number of factors $p$ in $Nfac(p,q)$.
+
+You are given that $NF(3,10000) \bmod 3^{20} = 624\\,955\\,285$.
+
+Find $NF(61,{10}^7)\bmod {61}^{10}$.
+
+# --hints--
+
+`enormousFactorial()` should return `605857431263982000`.
+
+```js
+assert.strictEqual(enormousFactorial(), 605857431263982000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function enormousFactorial() {
+
+ return true;
+}
+
+enormousFactorial();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-289-eulerian-cycles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-289-eulerian-cycles.md
new file mode 100644
index 00000000000..e491cab3612
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-289-eulerian-cycles.md
@@ -0,0 +1,50 @@
+---
+id: 5900f48d1000cf542c50ffa0
+title: 'Problem 289: Eulerian Cycles'
+challengeType: 1
+forumTopicId: 301940
+dashedName: problem-289-eulerian-cycles
+---
+
+# --description--
+
+Let $C(x,y)$ be a circle passing through the points ($x$, $y$), ($x$, $y + 1$), ($x + 1$, $y$) and ($x + 1$, $y + 1$).
+
+For positive integers $m$ and $n$, let $E(m,n)$ be a configuration which consists of the $m·n$ circles: { $C(x,y)$: $0 ≤ x < m$, $0 ≤ y < n$, $x$ and $y$ are integers }
+
+An Eulerian cycle on $E(m,n)$ is a closed path that passes through each arc exactly once. Many such paths are possible on $E(m,n)$, but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
+
+The image below shows $E(3,3)$ and an example of an Eulerian non-crossing path.
+
+
+
+Let $L(m,n)$ be the number of Eulerian non-crossing paths on $E(m,n)$. For example, $L(1,2) = 2$, $L(2,2) = 37$ and $L(3,3) = 104290$.
+
+Find $L(6,10)\bmod {10}^{10}$.
+
+# --hints--
+
+`eulerianCycles()` should return `6567944538`.
+
+```js
+assert.strictEqual(eulerianCycles(), 6567944538);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function eulerianCycles() {
+
+ return true;
+}
+
+eulerianCycles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-290-digital-signature.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-290-digital-signature.md
new file mode 100644
index 00000000000..a6b3636eefd
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-290-digital-signature.md
@@ -0,0 +1,38 @@
+---
+id: 5900f48f1000cf542c50ffa1
+title: 'Problem 290: Digital Signature'
+challengeType: 1
+forumTopicId: 301942
+dashedName: problem-290-digital-signature
+---
+
+# --description--
+
+How many integers $0 ≤ n < {10}^{18}$ have the property that the sum of the digits of $n$ equals the sum of digits of $137n$?
+
+# --hints--
+
+`digitalSignature()` should return `20444710234716470`.
+
+```js
+assert.strictEqual(digitalSignature(), 20444710234716470);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function digitalSignature() {
+
+ return true;
+}
+
+digitalSignature();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-291-panaitopol-primes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-291-panaitopol-primes.md
new file mode 100644
index 00000000000..bb33727271a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-291-panaitopol-primes.md
@@ -0,0 +1,40 @@
+---
+id: 5900f48f1000cf542c50ffa2
+title: 'Problem 291: Panaitopol Primes'
+challengeType: 1
+forumTopicId: 301943
+dashedName: problem-291-panaitopol-primes
+---
+
+# --description--
+
+A prime number $p$ is called a Panaitopol prime if $p = \frac{x^4 - y^4}{x^3 + y^3}$ for some positive integers $x$ and $y$.
+
+Find how many Panaitopol primes are less than $5 × {10}^{15}$.
+
+# --hints--
+
+`panaitopolPrimes()` should return `4037526`.
+
+```js
+assert.strictEqual(panaitopolPrimes(), 4037526);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function panaitopolPrimes() {
+
+ return true;
+}
+
+panaitopolPrimes();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-292-pythagorean-polygons.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-292-pythagorean-polygons.md
new file mode 100644
index 00000000000..8e0dd899454
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-292-pythagorean-polygons.md
@@ -0,0 +1,51 @@
+---
+id: 5900f4911000cf542c50ffa3
+title: 'Problem 292: Pythagorean Polygons'
+challengeType: 1
+forumTopicId: 301944
+dashedName: problem-292-pythagorean-polygons
+---
+
+# --description--
+
+We shall define a pythagorean polygon to be a convex polygon with the following properties:
+
+- there are at least three vertices,
+- no three vertices are aligned,
+- each vertex has integer coordinates,
+- each edge has integer length.
+
+For a given integer $n$, define $P(n)$ as the number of distinct pythagorean polygons for which the perimeter is $≤ n$.
+
+Pythagorean polygons should be considered distinct as long as none is a translation of another.
+
+You are given that $P(4) = 1$, $P(30) = 3655$ and $P(60) = 891045$.
+
+Find $P(120)$.
+
+# --hints--
+
+`pythagoreanPolygons()` should return `3600060866`.
+
+```js
+assert.strictEqual(pythagoreanPolygons(), 3600060866);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pythagoreanPolygons() {
+
+ return true;
+}
+
+pythagoreanPolygons();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-293-pseudo-fortunate-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-293-pseudo-fortunate-numbers.md
new file mode 100644
index 00000000000..0c8076828de
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-293-pseudo-fortunate-numbers.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4931000cf542c50ffa4
+title: 'Problem 293: Pseudo-Fortunate Numbers'
+challengeType: 1
+forumTopicId: 301945
+dashedName: problem-293-pseudo-fortunate-numbers
+---
+
+# --description--
+
+An even positive integer $N$ will be called admissible, if it is a power of 2 or its distinct prime factors are consecutive primes.
+
+The first twelve admissible numbers are 2, 4, 6, 8, 12, 16, 18, 24, 30, 32, 36, 48.
+
+If $N$ is admissible, the smallest integer $M > 1$ such that $N + M$ is prime, will be called the pseudo-Fortunate number for $N$.
+
+For example, $N = 630$ is admissible since it is even and its distinct prime factors are the consecutive primes 2, 3, 5 and 7. The next prime number after 631 is 641; hence, the pseudo-Fortunate number for 630 is $M = 11$. It can also be seen that the pseudo-Fortunate number for 16 is 3.
+
+Find the sum of all distinct pseudo-Fortunate numbers for admissible numbers $N$ less than ${10}^9$.
+
+# --hints--
+
+`pseudoFortunateNumbers()` should return `2209`.
+
+```js
+assert.strictEqual(pseudoFortunateNumbers(), 2209);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pseudoFortunateNumbers() {
+
+ return true;
+}
+
+pseudoFortunateNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-294-sum-of-digits---experience-23.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-294-sum-of-digits---experience-23.md
new file mode 100644
index 00000000000..b32ebc882de
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-294-sum-of-digits---experience-23.md
@@ -0,0 +1,47 @@
+---
+id: 5900f4931000cf542c50ffa5
+title: 'Problem 294: Sum of digits - experience #23'
+challengeType: 1
+forumTopicId: 301946
+dashedName: problem-294-sum-of-digits---experience-23
+---
+
+# --description--
+
+For a positive integer $k$, define $d(k)$ as the sum of the digits of $k$ in its usual decimal representation. Thus $d(42) = 4 + 2 = 6$.
+
+For a positive integer $n$, define $S(n)$ as the number of positive integers $k < {10}^n$ with the following properties:
+
+- $k$ is divisible by 23 and,
+- $d(k) = 23$.
+
+You are given that $S(9) = 263\\,626$ and $S(42) = 6\\,377\\,168\\,878\\,570\\,056$.
+
+Find $S({11}^{12})$ and give your answer $\bmod {10}^9$.
+
+# --hints--
+
+`experience23()` should return `789184709`.
+
+```js
+assert.strictEqual(experience23(), 789184709);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function experience23() {
+
+ return true;
+}
+
+experience23();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-295-lenticular-holes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-295-lenticular-holes.md
new file mode 100644
index 00000000000..9354ea7c840
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-295-lenticular-holes.md
@@ -0,0 +1,59 @@
+---
+id: 5900f4931000cf542c50ffa6
+title: 'Problem 295: Lenticular holes'
+challengeType: 1
+forumTopicId: 301947
+dashedName: problem-295-lenticular-holes
+---
+
+# --description--
+
+We call the convex area enclosed by two circles a lenticular hole if:
+
+- The centres of both circles are on lattice points.
+- The two circles intersect at two distinct lattice points.
+- The interior of the convex area enclosed by both circles does not contain any lattice points.
+
+Consider the circles:
+
+$$\begin{align} & C_0: x^2 + y^2 = 25 \\\\
+ & C_1: {(x + 4)}^2 + {(y - 4)}^2 = 1 \\\\ & C_2: {(x - 12)}^2 + {(y - 4)}^2 = 65 \end{align}$$
+
+The circles $C_0$, $C_1$ and $C_2$ are drawn in the picture below.
+
+
+
+$C_0$ and $C_1$ form a lenticular hole, as well as $C_0$ and $C_2$.
+
+We call an ordered pair of positive real numbers ($r_1$, $r_2$) a lenticular pair if there exist two circles with radii $r_1$ and $r_2$ that form a lenticular hole. We can verify that ($1$, $5$) and ($5$, $\sqrt{65}$) are the lenticular pairs of the example above.
+
+Let $L(N)$ be the number of distinct lenticular pairs ($r_1$, $r_2$) for which $0 < r_1 ≤ r_2 ≤ N$. We can verify that $L(10) = 30$ and $L(100) = 3442$.
+
+Find $L(100\\,000)$.
+
+# --hints--
+
+`lenticularHoles()` should return `4884650818`.
+
+```js
+assert.strictEqual(lenticularHoles(), 4884650818);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function lenticularHoles() {
+
+ return true;
+}
+
+lenticularHoles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-296-angular-bisector-and-tangent.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-296-angular-bisector-and-tangent.md
new file mode 100644
index 00000000000..660d66eabb4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-296-angular-bisector-and-tangent.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4941000cf542c50ffa7
+title: 'Problem 296: Angular Bisector and Tangent'
+challengeType: 1
+forumTopicId: 301948
+dashedName: problem-296-angular-bisector-and-tangent
+---
+
+# --description--
+
+Given is an integer sided triangle $ABC$ with $BC ≤ AC ≤ AB$. $k$ is the angular bisector of angle $ACB$. $m$ is the tangent at $C$ to the circumscribed circle of $ABC$. $n$ is a line parallel to $m$ through $B$.
+
+The intersection of $n$ and $k$ is called $E$.
+
+
+
+How many triangles $ABC$ with a perimeter not exceeding $100\\,000$ exist such that $BE$ has integral length?
+
+# --hints--
+
+`angularBisectorAndTangent()` should return `1137208419`.
+
+```js
+assert.strictEqual(angularBisectorAndTangent(), 1137208419);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function angularBisectorAndTangent() {
+
+ return true;
+}
+
+angularBisectorAndTangent();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-297-zeckendorf-representation.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-297-zeckendorf-representation.md
new file mode 100644
index 00000000000..55f3adbfd1c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-297-zeckendorf-representation.md
@@ -0,0 +1,52 @@
+---
+id: 5900f4951000cf542c50ffa8
+title: 'Problem 297: Zeckendorf Representation'
+challengeType: 1
+forumTopicId: 301949
+dashedName: problem-297-zeckendorf-representation
+---
+
+# --description--
+
+Each new term in the Fibonacci sequence is generated by adding the previous two terms.
+
+Starting with 1 and 2, the first 10 terms will be: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
+
+Every positive integer can be uniquely written as a sum of nonconsecutive terms of the Fibonacci sequence. For example, 100 = 3 + 8 + 89.
+
+Such a sum is called the Zeckendorf representation of the number.
+
+For any integer $n>0$, let $z(n)$ be the number of terms in the Zeckendorf representation of $n$.
+
+Thus, $z(5) = 1$, $z(14) = 2$, $z(100) = 3$ etc.
+
+Also, for $0 < n < {10}^6$, $\sum z(n) = 7\\,894\\,453$.
+
+Find $\sum z(n)$ for $0 < n < {10}^{17}$.
+
+# --hints--
+
+`zeckendorfRepresentation()` should return `2252639041804718000`.
+
+```js
+assert.strictEqual(zeckendorfRepresentation(), 2252639041804718000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function zeckendorfRepresentation() {
+
+ return true;
+}
+
+zeckendorfRepresentation();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-298-selective-amnesia.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-298-selective-amnesia.md
new file mode 100644
index 00000000000..da401b24b95
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-298-selective-amnesia.md
@@ -0,0 +1,57 @@
+---
+id: 5900f4971000cf542c50ffa9
+title: 'Problem 298: Selective Amnesia'
+challengeType: 1
+forumTopicId: 301950
+dashedName: problem-298-selective-amnesia
+---
+
+# --description--
+
+Larry and Robin play a memory game involving of a sequence of random numbers between 1 and 10, inclusive, that are called out one at a time. Each player can remember up to 5 previous numbers. When the called number is in a player's memory, that player is awarded a point. If it's not, the player adds the called number to his memory, removing another number if his memory is full.
+
+Both players start with empty memories. Both players always add new missed numbers to their memory but use a different strategy in deciding which number to remove: Larry's strategy is to remove the number that hasn't been called in the longest time. Robin's strategy is to remove the number that's been in the memory the longest time.
+
+Example game:
+
+| Turn | Called number | Larry's memory | Larry's score | Robin's memory | Robin's score |
+| ---- | ------------- | --------------:| ------------- | -------------- | ------------- |
+| 1 | 1 | 1 | 0 | 1 | 0 |
+| 2 | 2 | 1,2 | 0 | 1,2 | 0 |
+| 3 | 4 | 1,2,4 | 0 | 1,2,4 | 0 |
+| 4 | 6 | 1,2,4,6 | 0 | 1,2,4,6 | 0 |
+| 5 | 1 | 1,2,4,6 | 1 | 1,2,4,6 | 1 |
+| 6 | 8 | 1,2,4,6,8 | 1 | 1,2,4,6,8 | 1 |
+| 7 | 10 | 1,4,6,8,10 | 1 | 2,4,6,8,10 | 1 |
+| 8 | 2 | 1,2,6,8,10 | 1 | 2,4,6,8,10 | 2 |
+| 9 | 4 | 1,2,4,8,10 | 1 | 2,4,6,8,10 | 3 |
+| 10 | 1 | 1,2,4,8,10 | 2 | 1,4,6,8,10 | 3 |
+
+Denoting Larry's score by $L$ and Robin's score by $R$, what is the expected value of $|L - R|$ after 50 turns? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
+
+# --hints--
+
+`selectiveAmnesia()` should return `1.76882294`.
+
+```js
+assert.strictEqual(selectiveAmnesia(), 1.76882294);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function selectiveAmnesia() {
+
+ return true;
+}
+
+selectiveAmnesia();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-299-three-similar-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-299-three-similar-triangles.md
new file mode 100644
index 00000000000..5bd781949f5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-299-three-similar-triangles.md
@@ -0,0 +1,56 @@
+---
+id: 5900f4971000cf542c50ffaa
+title: 'Problem 299: Three similar triangles'
+challengeType: 1
+forumTopicId: 301951
+dashedName: problem-299-three-similar-triangles
+---
+
+# --description--
+
+Four points with integer coordinates are selected:
+
+$A(a, 0)$, $B(b, 0)$, $C(0, c)$ and $D(0, d)$, with $0 < a < b$ and $0 < c < d$.
+
+Point $P$, also with integer coordinates, is chosen on the line $AC$ so that the three triangles $ABP$, $CDP$ and $BDP$ are all similar.
+
+
+
+It is easy to prove that the three triangles can be similar, only if $a = c$.
+
+So, given that $a = c$, we are looking for triplets ($a$, $b$, $d$) such that at least one point $P$ (with integer coordinates) exists on $AC$, making the three triangles $ABP$, $CDP$ and $BDP$ all similar.
+
+For example, if $(a, b, d) = (2, 3, 4)$, it can be easily verified that point $P(1, 1)$ satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point $P(1, 1)$ is common for both.
+
+If $b + d < 100$, there are 92 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+
+If $b + d < 100\\,000$, there are 320471 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+
+If $b + d < 100\\,000\\,000$, how many distinct triplets ($a$, $b$, $d$) are there such that point $P$ exists?
+
+# --hints--
+
+`threeSimilarTriangles()` should return `549936643`.
+
+```js
+assert.strictEqual(threeSimilarTriangles(), 549936643);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function threeSimilarTriangles() {
+
+ return true;
+}
+
+threeSimilarTriangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-300-protein-folding.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-300-protein-folding.md
new file mode 100644
index 00000000000..d5f2020b784
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-201-to-300/problem-300-protein-folding.md
@@ -0,0 +1,56 @@
+---
+id: 5900f49a1000cf542c50ffac
+title: 'Problem 300: Protein folding'
+challengeType: 1
+forumTopicId: 301954
+dashedName: problem-300-protein-folding
+---
+
+# --description--
+
+In a very simplified form, we can consider proteins as strings consisting of hydrophobic (H) and polar (P) elements, e.g. HHPPHHHPHHPH.
+
+For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are $2^n$ distinct proteins consisting of $n$ elements.
+
+When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous.
+
+As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside.
+
+Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
+
+The figure below shows two possible ways that our example protein could be folded (H-H contact points are shown with red dots).
+
+
+
+The folding on the left has only six H-H contact points, thus it would never occur naturally. On the other hand, the folding on the right has nine H-H contact points, which is optimal for this string.
+
+Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be $\frac{850}{2^8} = 3.3203125$.
+
+What is the average number of H-H contact points in an optimal folding of a random protein string of length 15? Give your answer using as many decimal places as necessary for an exact result.
+
+# --hints--
+
+`proteinFolding()` should return `8.0540771484375`.
+
+```js
+assert.strictEqual(proteinFolding(), 8.0540771484375);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function proteinFolding() {
+
+ return true;
+}
+
+proteinFolding();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-301-nim.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-301-nim.md
new file mode 100644
index 00000000000..b66b1b9ae06
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-301-nim.md
@@ -0,0 +1,58 @@
+---
+id: 5900f4991000cf542c50ffab
+title: 'Problem 301: Nim'
+challengeType: 1
+forumTopicId: 301955
+dashedName: problem-301-nim
+---
+
+# --description--
+
+Nim is a game played with heaps of stones, where two players take it in turn to remove any number of stones from any heap until no stones remain.
+
+We'll consider the three-heap normal-play version of Nim, which works as follows:
+
+- At the start of the game there are three heaps of stones.
+- On his turn the player removes any positive number of stones from any single heap.
+- The first player unable to move (because no stones remain) loses.
+
+If ($n_1$, $n_2$, $n_3$) indicates a Nim position consisting of heaps of size $n_1$, $n_2$ and $n_3$ then there is a simple function $X(n_1,n_2,n_3)$ — that you may look up or attempt to deduce for yourself — that returns:
+
+- zero if, with perfect strategy, the player about to move will eventually lose; or
+- non-zero if, with perfect strategy, the player about to move will eventually win.
+
+For example $X(1, 2, 3) = 0$ because, no matter what the current player does, his opponent can respond with a move that leaves two heaps of equal size, at which point every move by the current player can be mirrored by his opponent until no stones remain; so the current player loses. To illustrate:
+
+- current player moves to (1,2,1)
+- opponent moves to (1,0,1)
+- current player moves to (0,0,1)
+- opponent moves to (0,0,0), and so wins.
+
+For how many positive integers $n ≤ 2^{30}$ does $X(n, 2n, 3n) = 0$?
+
+# --hints--
+
+`nim()` should return `2178309`.
+
+```js
+assert.strictEqual(nim(), 2178309);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function nim() {
+
+ return true;
+}
+
+nim();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-302-strong-achilles-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-302-strong-achilles-numbers.md
new file mode 100644
index 00000000000..4c5301c49bf
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-302-strong-achilles-numbers.md
@@ -0,0 +1,50 @@
+---
+id: 5900f49b1000cf542c50ffad
+title: 'Problem 302: Strong Achilles Numbers'
+challengeType: 1
+forumTopicId: 301956
+dashedName: problem-302-strong-achilles-numbers
+---
+
+# --description--
+
+A positive integer $n$ is powerful if $p^2$ is a divisor of $n$ for every prime factor $p$ in $n$.
+
+A positive integer $n$ is a perfect power if $n$ can be expressed as a power of another positive integer.
+
+A positive integer $n$ is an Achilles number if $n$ is powerful but not a perfect power. For example, 864 and 1800 are Achilles numbers: $864 = 2^5 \times 3^3$ and $1800 = 2^3 \times 3^2 \times 5^2$.
+
+We shall call a positive integer $S$ a Strong Achilles number if both $S$ and $φ(S)$ are Achilles numbers. $φ$ denotes Euler's totient function.
+
+For example, 864 is a Strong Achilles number: $φ(864) = 288 = 2^5 \times 3^2$. However, 1800 isn't a Strong Achilles number because: $φ(1800) = 480 = 2^5 \times 3^1 \times 5^1$.
+
+There are 7 Strong Achilles numbers below ${10}^4$ and 656 below ${10}^8$.
+
+How many Strong Achilles numbers are there below ${10}^{18}$?
+
+# --hints--
+
+`strongAchillesNumbers()` should return `1170060`.
+
+```js
+assert.strictEqual(strongAchillesNumbers(), 1170060);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function strongAchillesNumbers() {
+
+ return true;
+}
+
+strongAchillesNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-303-multiples-with-small-digits.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-303-multiples-with-small-digits.md
new file mode 100644
index 00000000000..108d8bd39fc
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-303-multiples-with-small-digits.md
@@ -0,0 +1,44 @@
+---
+id: 5900f49b1000cf542c50ffae
+title: 'Problem 303: Multiples with small digits'
+challengeType: 1
+forumTopicId: 301957
+dashedName: problem-303-multiples-with-small-digits
+---
+
+# --description--
+
+For a positive integer $n$, define $f(n)$ as the least positive multiple of $n$ that, written in base 10, uses only digits $≤ 2$.
+
+Thus $f(2) = 2$, $f(3) = 12$, $f(7) = 21$, $f(42) = 210$, $f(89) = 1\\,121\\,222$.
+
+Also, $\displaystyle\sum_{n = 1}^{100} \frac{f(n)}{n} = 11\\,363\\,107$.
+
+Find $\displaystyle\sum_{n = 1}^{10\\,000} \frac{f(n)}{n}$.
+
+# --hints--
+
+`multiplesWithSmallDigits()` should return `1111981904675169`.
+
+```js
+assert.strictEqual(multiplesWithSmallDigits(), 1111981904675169);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function multiplesWithSmallDigits() {
+
+ return true;
+}
+
+multiplesWithSmallDigits();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-304-primonacci.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-304-primonacci.md
new file mode 100644
index 00000000000..a4939940a8f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-304-primonacci.md
@@ -0,0 +1,46 @@
+---
+id: 5900f49d1000cf542c50ffaf
+title: 'Problem 304: Primonacci'
+challengeType: 1
+forumTopicId: 301958
+dashedName: problem-304-primonacci
+---
+
+# --description--
+
+For any positive integer $n$ the function $\text{next_prime}(n)$ returns the smallest prime $p$ such that $p > n$.
+
+The sequence $a(n)$ is defined by: $a(1) = \text{next_prime}({10}^{14})$ and $a(n) = \text{next_prime}(a(n - 1))$ for $n > 1$.
+
+The fibonacci sequence $f(n)$ is defined by: $f(0) = 0$, $f(1) = 1$ and $f(n) = f(n - 1) + f(n - 2)$ for $n > 1$.
+
+The sequence $b(n)$ is defined as $f(a(n))$.
+
+Find $\sum b(n)$ for $1≤n≤100\\,000$. Give your answer $\bmod 1\\,234\\,567\\,891\\,011$.
+
+# --hints--
+
+`primonacci()` should return `283988410192`.
+
+```js
+assert.strictEqual(primonacci(), 283988410192);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primonacci() {
+
+ return true;
+}
+
+primonacci();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-305-reflexive-position.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-305-reflexive-position.md
new file mode 100644
index 00000000000..566e7b7b76c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-305-reflexive-position.md
@@ -0,0 +1,46 @@
+---
+id: 5900f49d1000cf542c50ffb0
+title: 'Problem 305: Reflexive Position'
+challengeType: 1
+forumTopicId: 301959
+dashedName: problem-305-reflexive-position
+---
+
+# --description--
+
+Let's call $S$ the (infinite) string that is made by concatenating the consecutive positive integers (starting from 1) written down in base 10.
+
+Thus, $S = 1234567891011121314151617181920212223242\ldots$
+
+It's easy to see that any number will show up an infinite number of times in $S$.
+
+Let's call $f(n)$ the starting position of the $n^{\text{th}}$ occurrence of $n$ in $S$. For example, $f(1) = 1$, $f(5) = 81$, $f(12) = 271$ and $f(7780) = 111\\,111\\,365$.
+
+Find $\sum f(3^k) for 1 ≤ k ≤ 13$.
+
+# --hints--
+
+`reflexivePosition()` should return `18174995535140`.
+
+```js
+assert.strictEqual(reflexivePosition(), 18174995535140);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function reflexivePosition() {
+
+ return true;
+}
+
+reflexivePosition();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-306-paper-strip-game.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-306-paper-strip-game.md
new file mode 100644
index 00000000000..3dd4604bc13
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-306-paper-strip-game.md
@@ -0,0 +1,54 @@
+---
+id: 5900f49f1000cf542c50ffb1
+title: 'Problem 306: Paper-strip Game'
+challengeType: 1
+forumTopicId: 301960
+dashedName: problem-306-paper-strip-game
+---
+
+# --description--
+
+The following game is a classic example of Combinatorial Game Theory:
+
+Two players start with a strip of $n$ white squares and they take alternate turns. On each turn, a player picks two contiguous white squares and paints them black. The first player who cannot make a move loses.
+
+- $n = 1$: No valid moves, so the first player loses automatically.
+- $n = 2$: Only one valid move, after which the second player loses.
+- $n = 3$: Two valid moves, but both leave a situation where the second player loses.
+- $n = 4$: There are three valid moves for the first player; who is able to win the game by painting the two middle squares.
+- $n = 5$: Four valid moves for the first player (shown below in red); but no matter what the player does, the second player (blue) wins.
+
+
+
+So, for $1 ≤ n ≤ 5$, there are 3 values of $n$ for which the first player can force a win.
+
+Similarly, for $1 ≤ n ≤ 50$, there are 40 values of $n$ for which the first player can force a win.
+
+For $1 ≤ n ≤ 1\\,000\\,000$, how many values of $n$ are there for which the first player can force a win?
+
+# --hints--
+
+`paperStripGame()` should return `852938`.
+
+```js
+assert.strictEqual(paperStripGame(), 852938);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function paperStripGame() {
+
+ return true;
+}
+
+paperStripGame();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-307-chip-defects.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-307-chip-defects.md
new file mode 100644
index 00000000000..3f0fd2be0cb
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-307-chip-defects.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4a01000cf542c50ffb2
+title: 'Problem 307: Chip Defects'
+challengeType: 1
+forumTopicId: 301961
+dashedName: problem-307-chip-defects
+---
+
+# --description--
+
+$k$ defects are randomly distributed amongst $n$ integrated-circuit chips produced by a factory (any number of defects may be found on a chip and each defect is independent of the other defects).
+
+Let $p(k,n)$ represent the probability that there is a chip with at least 3 defects. For instance $p(3,7) ≈ 0.0204081633$.
+
+Find $p(20\\,000, 1\\,000\\,000)$ and give your answer rounded to 10 decimal places in the form 0.abcdefghij
+
+# --hints--
+
+`chipDefects()` should return `0.7311720251`.
+
+```js
+assert.strictEqual(chipDefects(), 0.7311720251);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function chipDefects() {
+
+ return true;
+}
+
+chipDefects();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-308-an-amazing-prime-generating-automaton.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-308-an-amazing-prime-generating-automaton.md
new file mode 100644
index 00000000000..22f3cabc900
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-308-an-amazing-prime-generating-automaton.md
@@ -0,0 +1,54 @@
+---
+id: 5900f4a11000cf542c50ffb3
+title: 'Problem 308: An amazing Prime-generating Automaton'
+challengeType: 1
+forumTopicId: 301962
+dashedName: problem-308-an-amazing-prime-generating-automaton
+---
+
+# --description--
+
+A program written in the programming language Fractran consists of a list of fractions.
+
+The internal state of the Fractran Virtual Machine is a positive integer, which is initially set to a seed value. Each iteration of a Fractran program multiplies the state integer by the first fraction in the list which will leave it an integer.
+
+For example, one of the Fractran programs that John Horton Conway wrote for prime-generation consists of the following 14 fractions:
+
+$$\frac{17}{91}, \frac{78}{85}, \frac{19}{51}, \frac{23}{38}, \frac{29}{33}, \frac{77}{29}, \frac{95}{23}, \frac{77}{19}, \frac{1}{17}, \frac{11}{13}, \frac{13}{11}, \frac{15}{2}, \frac{1}{7}, \frac{55}{1}$$
+
+Starting with the seed integer 2, successive iterations of the program produce the sequence:
+
+$$15, 825, 725, 1925, 2275, 425, \ldots, 68, \mathbf{4}, 30, \ldots, 136, \mathbf{8}, 60, \ldots, 544, \mathbf{32}, 240, \ldots$$
+
+The powers of 2 that appear in this sequence are $2^2, 2^3, 2^5, \ldots$.
+
+It can be shown that all the powers of 2 in this sequence have prime exponents and that all the primes appear as exponents of powers of 2, in proper order!
+
+If someone uses the above Fractran program to solve Project Euler Problem 7 (find the ${10001}^{\text{st}}$ prime), how many iterations would be needed until the program produces $2^{10001^{\text{st}}\text{ prime}}$?
+
+# --hints--
+
+`primeGeneratingAutomation()` should return `1539669807660924`.
+
+```js
+assert.strictEqual(primeGeneratingAutomation(), 1539669807660924);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeGeneratingAutomation() {
+
+ return true;
+}
+
+primeGeneratingAutomation();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-309-integer-ladders.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-309-integer-ladders.md
new file mode 100644
index 00000000000..721b756f533
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-309-integer-ladders.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4a11000cf542c50ffb4
+title: 'Problem 309: Integer Ladders'
+challengeType: 1
+forumTopicId: 301963
+dashedName: problem-309-integer-ladders
+---
+
+# --description--
+
+In the classic "Crossing Ladders" problem, we are given the lengths $x$ and $y$ of two ladders resting on the opposite walls of a narrow, level street. We are also given the height $h$ above the street where the two ladders cross and we are asked to find the width of the street ($w$).
+
+
+
+Here, we are only concerned with instances where all four variables are positive integers. For example, if $x = 70$, $y = 119$ and $h = 30$, we can calculate that $w = 56$.
+
+In fact, for integer values $x$, $y$, $h$ and $0 < x < y < 200$, there are only five triplets ($x$, $y$, $h$) producing integer solutions for $w$: (70, 119, 30), (74, 182, 21), (87, 105, 35), (100, 116, 35) and (119, 175, 40).
+
+For integer values $x$, $y$, $h$ and $0 < x < y < 1\\,000\\,000$, how many triplets ($x$, $y$, $h$) produce integer solutions for $w$?
+
+# --hints--
+
+`integerLadders()` should return `210139`.
+
+```js
+assert.strictEqual(integerLadders(), 210139);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function integerLadders() {
+
+ return true;
+}
+
+integerLadders();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-310-nim-square.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-310-nim-square.md
new file mode 100644
index 00000000000..4eacb352843
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-310-nim-square.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4a21000cf542c50ffb5
+title: 'Problem 310: Nim Square'
+challengeType: 1
+forumTopicId: 301966
+dashedName: problem-310-nim-square
+---
+
+# --description--
+
+Alice and Bob play the game Nim Square.
+
+Nim Square is just like ordinary three-heap normal play Nim, but the players may only remove a square number of stones from a heap.
+
+The number of stones in the three heaps is represented by the ordered triple ($a$, $b$, $c$).
+
+If $0 ≤ a ≤ b ≤ c ≤ 29$ then the number of losing positions for the next player is 1160.
+
+Find the number of losing positions for the next player if $0 ≤ a ≤ b ≤ c ≤ 100\\,000$.
+
+# --hints--
+
+`nimSquare()` should return `2586528661783`.
+
+```js
+assert.strictEqual(nimSquare(), 2586528661783);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function nimSquare() {
+
+ return true;
+}
+
+nimSquare();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-311-biclinic-integral-quadrilaterals.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-311-biclinic-integral-quadrilaterals.md
new file mode 100644
index 00000000000..97736d98034
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-311-biclinic-integral-quadrilaterals.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4a31000cf542c50ffb6
+title: 'Problem 311: Biclinic Integral Quadrilaterals'
+challengeType: 1
+forumTopicId: 301967
+dashedName: problem-311-biclinic-integral-quadrilaterals
+---
+
+# --description--
+
+$ABCD$ is a convex, integer sided quadrilateral with $1 ≤ AB < BC < CD < AD$.
+
+$BD$ has integer length. $O$ is the midpoint of $BD$. $AO$ has integer length.
+
+We'll call $ABCD$ a biclinic integral quadrilateral if $AO = CO ≤ BO = DO$.
+
+For example, the following quadrilateral is a biclinic integral quadrilateral: $AB = 19$, $BC = 29$, $CD = 37$, $AD = 43$, $BD = 48$ and $AO = CO = 23$.
+
+
+
+Let $B(N)$ be the number of distinct biclinic integral quadrilaterals $ABCD$ that satisfy ${AB}^2 + {BC}^2 + {CD}^2 + {AD}^2 ≤ N$. We can verify that $B(10\\,000) = 49$ and $B(1\\,000\\,000) = 38239$.
+
+Find $B(10\\,000\\,000\\,000)$.
+
+# --hints--
+
+`biclinicIntegralQuadrilaterals()` should return `2466018557`.
+
+```js
+assert.strictEqual(biclinicIntegralQuadrilaterals(), 2466018557);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function biclinicIntegralQuadrilaterals() {
+
+ return true;
+}
+
+biclinicIntegralQuadrilaterals();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-312-cyclic-paths-on-sierpiski-graphs.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-312-cyclic-paths-on-sierpiski-graphs.md
new file mode 100644
index 00000000000..122f28f97dc
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-312-cyclic-paths-on-sierpiski-graphs.md
@@ -0,0 +1,53 @@
+---
+id: 5900f4a51000cf542c50ffb7
+title: 'Problem 312: Cyclic paths on Sierpiński graphs'
+challengeType: 1
+forumTopicId: 301968
+dashedName: problem-312-cyclic-paths-on-sierpiski-graphs
+---
+
+# --description--
+
+- A Sierpiński graph of order-1 ($S_1$) is an equilateral triangle.
+- $S_{n + 1}$ is obtained from $S_n$ by positioning three copies of $S_n$ so that every pair of copies has one common corner.
+
+
+
+Let $C(n)$ be the number of cycles that pass exactly once through all the vertices of $S_n$. For example, $C(3) = 8$ because eight such cycles can be drawn on $S_3$, as shown below:
+
+
+
+It can also be verified that:
+
+$$\begin{align} & C(1) = C(2) = 1 \\\\
+ & C(5) = 71\\,328\\,803\\,586\\,048 \\\\ & C(10 000)\bmod {10}^8 = 37\\,652\\,224 \\\\
+ & C(10 000)\bmod {13}^8 = 617\\,720\\,485 \\\\ \end{align}$$
+
+Find $C(C(C(10\\,000)))\bmod {13}^8$.
+
+# --hints--
+
+`pathsOnSierpinskiGraphs()` should return `324681947`.
+
+```js
+assert.strictEqual(pathsOnSierpinskiGraphs(), 324681947);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pathsOnSierpinskiGraphs() {
+
+ return true;
+}
+
+pathsOnSierpinskiGraphs();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-313-sliding-game.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-313-sliding-game.md
new file mode 100644
index 00000000000..8f5726b71f4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-313-sliding-game.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4a61000cf542c50ffb8
+title: 'Problem 313: Sliding game'
+challengeType: 1
+forumTopicId: 301969
+dashedName: problem-313-sliding-game
+---
+
+# --description--
+
+In a sliding game a counter may slide horizontally or vertically into an empty space. The objective of the game is to move the red counter from the top left corner of a grid to the bottom right corner; the space always starts in the bottom right corner. For example, the following sequence of pictures show how the game can be completed in five moves on a 2 by 2 grid.
+
+
+
+Let $S(m, n)$ represent the minimum number of moves to complete the game on an $m$ by $n$ grid. For example, it can be verified that $S(5, 4) = 25$.
+
+
+
+There are exactly 5482 grids for which $S(m, n) = p^2$, where $p < 100$ is prime.
+
+How many grids does $S(m, n) = p^2$, where $p < {10}^6$ is prime?
+
+# --hints--
+
+`slidingGame()` should return `2057774861813004`.
+
+```js
+assert.strictEqual(slidingGame(), 2057774861813004);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function slidingGame() {
+
+ return true;
+}
+
+slidingGame();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-314-the-mouse-on-the-moon.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-314-the-mouse-on-the-moon.md
new file mode 100644
index 00000000000..899395668c7
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-314-the-mouse-on-the-moon.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4a71000cf542c50ffb9
+title: 'Problem 314: The Mouse on the Moon'
+challengeType: 1
+forumTopicId: 301970
+dashedName: problem-314-the-mouse-on-the-moon
+---
+
+# --description--
+
+The moon has been opened up, and land can be obtained for free, but there is a catch. You have to build a wall around the land that you stake out, and building a wall on the moon is expensive. Every country has been allotted a 500 m by 500 m square area, but they will possess only that area which they wall in. 251001 posts have been placed in a rectangular grid with 1 meter spacing. The wall must be a closed series of straight lines, each line running from post to post.
+
+The bigger countries of course have built a 2000 m wall enclosing the entire 250 000 $\text{m}^2$ area. The Duchy of Grand Fenwick, has a tighter budget, and has asked you (their Royal Programmer) to compute what shape would get best maximum $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio.
+
+You have done some preliminary calculations on a sheet of paper. For a 2000 meter wall enclosing the 250 000 $\text{m}^2$ area the $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio is 125.
+
+Although not allowed, but to get an idea if this is anything better: if you place a circle inside the square area touching the four sides the area will be equal to $π \times {250}^2 \text{m}^2$ and the perimeter will be $π \times 500 \text{m}$, so the $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio will also be 125.
+
+However, if you cut off from the square four triangles with sides 75 m, 75 m and $75\sqrt{2}$ m the total area becomes 238750 $\text{m}^2$ and the perimeter becomes $1400 + 300\sqrt{2}$ m. So this gives an $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio of 130.87, which is significantly better.
+
+
+
+Find the maximum $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio. Give your answer rounded to 8 places behind the decimal point in the form abc.defghijk.
+
+# --hints--
+
+`theMouseOnTheMoon()` should return `132.52756426`.
+
+```js
+assert.strictEqual(theMouseOnTheMoon(), 132.52756426);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function theMouseOnTheMoon() {
+
+ return true;
+}
+
+theMouseOnTheMoon();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-315-digital-root-clocks.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-315-digital-root-clocks.md
new file mode 100644
index 00000000000..59389d4a7ff
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-315-digital-root-clocks.md
@@ -0,0 +1,72 @@
+---
+id: 5900f4a71000cf542c50ffba
+title: 'Problem 315: Digital root clocks'
+challengeType: 1
+forumTopicId: 301971
+dashedName: problem-315-digital-root-clocks
+---
+
+# --description--
+
+
+
+Sam and Max are asked to transform two digital clocks into two "digital root" clocks.
+
+A digital root clock is a digital clock that calculates digital roots step by step.
+
+When a clock is fed a number, it will show it and then it will start the calculation, showing all the intermediate values until it gets to the result. For example, if the clock is fed the number 137, it will show: `137` → `11` → `2` and then it will go black, waiting for the next number.
+
+Every digital number consists of some light segments: three horizontal (top, middle, bottom) and four vertical (top-left, top-right, bottom-left, bottom-right). Number `1` is made of vertical top-right and bottom-right, number `4` is made by middle horizontal and vertical top-left, top-right and bottom-right. Number `8` lights them all.
+
+The clocks consume energy only when segments are turned on/off. To turn on a `2` will cost 5 transitions, while a `7` will cost only 4 transitions.
+
+Sam and Max built two different clocks.
+
+Sam's clock is fed e.g. number 137: the clock shows `137`, then the panel is turned off, then the next number (`11`) is turned on, then the panel is turned off again and finally the last number (`2`) is turned on and, after some time, off.
+
+For the example, with number 137, Sam's clock requires:
+
+- `137`: $(2 + 5 + 4) × 2 = 22$ transitions (`137` on/off).
+- `11`: $(2 + 2) × 2 = 8$ transitions (`11` on/off).
+- `2`: $(5) × 2 = 10$ transitions (`2` on/off).
+
+For a grand total of 40 transitions.
+
+Max's clock works differently. Instead of turning off the whole panel, it is smart enough to turn off only those segments that won't be needed for the next number.
+
+For number 137, Max's clock requires:
+
+- `137` : $2 + 5 + 4 = 11$ transitions (`137` on), $7$ transitions (to turn off the segments that are not needed for number `11`).
+- `11` : $0$ transitions (number `11` is already turned on correctly), $3$ transitions (to turn off the first `1` and the bottom part of the second `1`; the top part is common with number `2`).
+- `2` : $4$ transitions (to turn on the remaining segments in order to get a `2`), $5$ transitions (to turn off number `2`).
+
+For a grand total of 30 transitions.
+
+Of course, Max's clock consumes less power than Sam's one. The two clocks are fed all the prime numbers between $A = {10}^7$ and $B = 2 × {10}^7$. Find the difference between the total number of transitions needed by Sam's clock and that needed by Max's one.
+
+# --hints--
+
+`digitalRootClocks()` should return `13625242`.
+
+```js
+assert.strictEqual(digitalRootClocks(), 13625242);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function digitalRootClocks() {
+
+ return true;
+}
+
+digitalRootClocks();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-316-numbers-in-decimal-expansions.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-316-numbers-in-decimal-expansions.md
new file mode 100644
index 00000000000..991df99ffa1
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-316-numbers-in-decimal-expansions.md
@@ -0,0 +1,58 @@
+---
+id: 5900f4a81000cf542c50ffbb
+title: 'Problem 316: Numbers in decimal expansions'
+challengeType: 1
+forumTopicId: 301972
+dashedName: problem-316-numbers-in-decimal-expansions
+---
+
+# --description--
+
+Let $p = p_1 p_2 p_3 \ldots$ be an infinite sequence of random digits, selected from {0,1,2,3,4,5,6,7,8,9} with equal probability.
+
+It can be seen that $p$ corresponds to the real number $0.p_1 p_2 p_3 \ldots$.
+
+It can also be seen that choosing a random real number from the interval [0,1) is equivalent to choosing an infinite sequence of random digits selected from {0,1,2,3,4,5,6,7,8,9} with equal probability.
+
+For any positive integer $n$ with $d$ decimal digits, let $k$ be the smallest index such that $p_k, p_{k + 1}, \ldots p_{k + d - 1}$ are the decimal digits of $n$, in the same order.
+
+Also, let $g(n)$ be the expected value of $k$; it can be proven that $g(n)$ is always finite and, interestingly, always an integer number.
+
+For example, if $n = 535$, then
+
+for $p = 31415926\mathbf{535}897\ldots$, we get $k = 9$
+
+for $p = 35528714365004956000049084876408468\mathbf{535}4\ldots$, we get $k = 36$
+
+etc and we find that $g(535) = 1008$.
+
+Given that $\displaystyle\sum_{n = 2}^{999} g\left(\left\lfloor\frac{{10}^6}{n}\right\rfloor\right) = 27280188$, find $\displaystyle\sum_{n = 2}^{999\\,999} g\left(\left\lfloor\frac{{10}^{16}}{n}\right\rfloor\right)$.
+
+**Note:** $\lfloor x\rfloor$ represents the floor function.
+
+# --hints--
+
+`numbersInDecimalExpansion()` should return `542934735751917760`.
+
+```js
+assert.strictEqual(numbersInDecimalExpansion(), 542934735751917760);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function numbersInDecimalExpansion() {
+
+ return true;
+}
+
+numbersInDecimalExpansion();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-317-firecracker.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-317-firecracker.md
new file mode 100644
index 00000000000..f9715cfd8df
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-317-firecracker.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4aa1000cf542c50ffbc
+title: 'Problem 317: Firecracker'
+challengeType: 1
+forumTopicId: 301973
+dashedName: problem-317-firecracker
+---
+
+# --description--
+
+A firecracker explodes at a height of 100 m above level ground. It breaks into a large number of very small fragments, which move in every direction; all of them have the same initial velocity of 20 $\frac{\text{m}}{\text{s}}$.
+
+We assume that the fragments move without air resistance, in a uniform gravitational field with $g=9.81 \frac{\text{m}}{\text{s}^2}$.
+
+Find the volume (in $\text{m}^3$) of the region through which the fragments move before reaching the ground. Give your answer rounded to four decimal places.
+
+# --hints--
+
+`firecracker()` should return `1856532.8455`.
+
+```js
+assert.strictEqual(firecracker(), 1856532.8455);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function firecracker() {
+
+ return true;
+}
+
+firecracker();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-318-2011-nines.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-318-2011-nines.md
new file mode 100644
index 00000000000..f4b4f8315b5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-318-2011-nines.md
@@ -0,0 +1,56 @@
+---
+id: 5900f4ab1000cf542c50ffbd
+title: 'Problem 318: 2011 nines'
+challengeType: 1
+forumTopicId: 301974
+dashedName: problem-318-2011-nines
+---
+
+# --description--
+
+Consider the real number $\sqrt{2} + \sqrt{3}$.
+
+When we calculate the even powers of $\sqrt{2} + \sqrt{3}$ we get:
+
+$$\begin{align} & {(\sqrt{2} + \sqrt{3})}^2 = 9.898979485566356\ldots \\\\
+ & {(\sqrt{2} + \sqrt{3})}^4 = 97.98979485566356\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^6 = 969.998969071069263\ldots \\\\
+ & {(\sqrt{2} + \sqrt{3})}^8 = 9601.99989585502907\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^{10} = 95049.999989479221\ldots \\\\
+ & {(\sqrt{2} + \sqrt{3})}^{12} = 940897.9999989371855\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^{14} = 9313929.99999989263\ldots \\\\
+ & {(\sqrt{2} + \sqrt{3})}^{16} = 92198401.99999998915\ldots \\\\ \end{align}$$
+
+It looks like that the number of consecutive nines at the beginning of the fractional part of these powers is non-decreasing. In fact it can be proven that the fractional part of ${(\sqrt{2} + \sqrt{3})}^{2n}$ approaches 1 for large $n$.
+
+Consider all real numbers of the form $\sqrt{p} + \sqrt{q}$ with $p$ and $q$ positive integers and $p < q$, such that the fractional part of ${(\sqrt{p} + \sqrt{q})}^{2n}$ approaches 1 for large $n$.
+
+Let $C(p,q,n)$ be the number of consecutive nines at the beginning of the fractional part of ${(\sqrt{p} + \sqrt{q})}^{2n}$.
+
+Let $N(p,q)$ be the minimal value of $n$ such that $C(p,q,n) ≥ 2011$.
+
+Find $\sum N(p,q)$ for $p + q ≤ 2011$.
+
+# --hints--
+
+`twoThousandElevenNines()` should return `709313889`.
+
+```js
+assert.strictEqual(twoThousandElevenNines(), 709313889);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function twoThousandElevenNines() {
+
+ return true;
+}
+
+twoThousandElevenNines();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-319-bounded-sequences.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-319-bounded-sequences.md
new file mode 100644
index 00000000000..36341fac54b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-319-bounded-sequences.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4ab1000cf542c50ffbe
+title: 'Problem 319: Bounded Sequences'
+challengeType: 1
+forumTopicId: 301975
+dashedName: problem-319-bounded-sequences
+---
+
+# --description--
+
+Let $x_1, x_2, \ldots, x_n$ be a sequence of length $n$ such that:
+
+- $x_1 = 2$
+- for all $1 < i ≤ n : x_{i - 1} < x_i$
+- for all $i$ and $j$ with $1 ≤ i, j ≤ n : {(x_i)}^j < {(x_j + 1)}^i$
+
+There are only five such sequences of length 2, namely: {2,4}, {2,5}, {2,6}, {2,7} and {2,8}. There are 293 such sequences of length 5; three examples are given below: {2,5,11,25,55}, {2,6,14,36,88}, {2,8,22,64,181}.
+
+Let $t(n)$ denote the number of such sequences of length $n$. You are given that $t(10) = 86195$ and $t(20) = 5227991891$.
+
+Find $t({10}^{10})$ and give your answer modulo $10^9$.
+
+# --hints--
+
+`boundedSequences()` should return `268457129`.
+
+```js
+assert.strictEqual(boundedSequences(), 268457129);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function boundedSequences() {
+
+ return true;
+}
+
+boundedSequences();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-320-factorials-divisible-by-a-huge-integer.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-320-factorials-divisible-by-a-huge-integer.md
new file mode 100644
index 00000000000..b0f0cc5c6ae
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-320-factorials-divisible-by-a-huge-integer.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4ae1000cf542c50ffbf
+title: 'Problem 320: Factorials divisible by a huge integer'
+challengeType: 1
+forumTopicId: 301977
+dashedName: problem-320-factorials-divisible-by-a-huge-integer
+---
+
+# --description--
+
+Let $N(i)$ be the smallest integer $n$ such that $n!$ is divisible by $(i!)^{1234567890}$
+
+Let $S(u) = \sum N(i)$ for $10 ≤ i ≤ u$.
+
+$S(1000)=614\\,538\\,266\\,565\\,663$.
+
+Find $S(1\\,000\\,000)\bmod {10}^{18}$.
+
+# --hints--
+
+`divisibleByHugeInteger()` should return `278157919195482660`.
+
+```js
+assert.strictEqual(divisibleByHugeInteger(), 278157919195482660);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function divisibleByHugeInteger() {
+
+ return true;
+}
+
+divisibleByHugeInteger();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-321-swapping-counters.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-321-swapping-counters.md
new file mode 100644
index 00000000000..177610fd3c7
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-321-swapping-counters.md
@@ -0,0 +1,52 @@
+---
+id: 5900f4ae1000cf542c50ffc0
+title: 'Problem 321: Swapping Counters'
+challengeType: 1
+forumTopicId: 301978
+dashedName: problem-321-swapping-counters
+---
+
+# --description--
+
+A horizontal row comprising of $2n + 1$ squares has $n$ red counters placed at one end and $n$ blue counters at the other end, being separated by a single empty square in the center. For example, when $n = 3$.
+
+
+
+A counter can move from one square to the next (slide) or can jump over another counter (hop) as long as the square next to that counter is unoccupied.
+
+
+
+Let $M(n)$ represent the minimum number of moves/actions to completely reverse the positions of the colored counters; that is, move all the red counters to the right and all the blue counters to the left.
+
+It can be verified $M(3) = 15$, which also happens to be a triangle number.
+
+If we create a sequence based on the values of n for which $M(n)$ is a triangle number then the first five terms would be: 1, 3, 10, 22, and 63, and their sum would be 99.
+
+Find the sum of the first forty terms of this sequence.
+
+# --hints--
+
+`swappingCounters()` should return `2470433131948040`.
+
+```js
+assert.strictEqual(swappingCounters(), 2470433131948040);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function swappingCounters() {
+
+ return true;
+}
+
+swappingCounters();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-322-binomial-coefficients-divisible-by-10.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-322-binomial-coefficients-divisible-by-10.md
new file mode 100644
index 00000000000..2c1725a5c4b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-322-binomial-coefficients-divisible-by-10.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4af1000cf542c50ffc1
+title: 'Problem 322: Binomial coefficients divisible by 10'
+challengeType: 1
+forumTopicId: 301979
+dashedName: problem-322-binomial-coefficients-divisible-by-10
+---
+
+# --description--
+
+Let $T(m, n)$ be the number of the binomial coefficients ${}^iC_n$ that are divisible by 10 for $n ≤ i < m$ ($i$, $m$ and $n$ are positive integers).
+
+You are given that $T({10}^9, {10}^7 - 10) = 989\\,697\\,000$.
+
+Find $T({10}^{18}, {10}^{12} - 10)$.
+
+# --hints--
+
+`binomialCoefficientsDivisibleBy10()` should return `999998760323314000`.
+
+```js
+assert.strictEqual(binomialCoefficientsDivisibleBy10(), 999998760323314000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function binomialCoefficientsDivisibleBy10() {
+
+ return true;
+}
+
+binomialCoefficientsDivisibleBy10();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-323-bitwise-or-operations-on-random-integers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-323-bitwise-or-operations-on-random-integers.md
new file mode 100644
index 00000000000..7cd5acf36cc
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-323-bitwise-or-operations-on-random-integers.md
@@ -0,0 +1,47 @@
+---
+id: 5900f4b01000cf542c50ffc2
+title: 'Problem 323: Bitwise-OR operations on random integers'
+challengeType: 1
+forumTopicId: 301980
+dashedName: problem-323-bitwise-or-operations-on-random-integers
+---
+
+# --description--
+
+Let $y_0, y_1, y_2, \ldots$ be a sequence of random unsigned 32 bit integers (i.e. $0 ≤ y_i < 2^{32}$, every value equally likely).
+
+For the sequence $x_i$ the following recursion is given:
+
+- $x_0 = 0$ and
+- $x_i = x_{i - 1} \mathbf{|} y_{i - 1}$, for $i > 0$. ($\mathbf{|}$ is the bitwise-OR operator)
+
+It can be seen that eventually there will be an index $N$ such that $x_i = 2^{32} - 1$ (a bit-pattern of all ones) for all $i ≥ N$.
+
+Find the expected value of $N$. Give your answer rounded to 10 digits after the decimal point.
+
+# --hints--
+
+`bitwiseOrOnRandomIntegers()` should return `6.3551758451`.
+
+```js
+assert.strictEqual(bitwiseOrOnRandomIntegers(), 6.3551758451);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function bitwiseOrOnRandomIntegers() {
+
+ return true;
+}
+
+bitwiseOrOnRandomIntegers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-324-building-a-tower.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-324-building-a-tower.md
new file mode 100644
index 00000000000..e79296a5f0f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-324-building-a-tower.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4b11000cf542c50ffc3
+title: 'Problem 324: Building a tower'
+challengeType: 1
+forumTopicId: 301981
+dashedName: problem-324-building-a-tower
+---
+
+# --description--
+
+Let $f(n)$ represent the number of ways one can fill a $3×3×n$ tower with blocks of $2×1×1$. You're allowed to rotate the blocks in any way you like; however, rotations, reflections etc of the tower itself are counted as distinct.
+
+For example (with $q = 100\\,000\\,007$):
+
+$$\begin{align} & f(2) = 229, \\\\
+ & f(4) = 117\\,805, \\\\ & f(10)\bmod q = 96\\,149\\,360, \\\\
+ & f({10}^3)\bmod q = 24\\,806\\,056, \\\\ & f({10}^6)\bmod q = 30\\,808\\,124. \end{align}$$
+
+Find $f({10}^{10000})\bmod 100\\,000\\,007$.
+
+# --hints--
+
+`buildingTower()` should return `96972774`.
+
+```js
+assert.strictEqual(buildingTower(), 96972774);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function buildingTower() {
+
+ return true;
+}
+
+buildingTower();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-325-stone-game-ii.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-325-stone-game-ii.md
new file mode 100644
index 00000000000..b1392c1e246
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-325-stone-game-ii.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4b11000cf542c50ffc4
+title: 'Problem 325: Stone Game II'
+challengeType: 1
+forumTopicId: 301982
+dashedName: problem-325-stone-game-ii
+---
+
+# --description--
+
+A game is played with two piles of stones and two players. On each player's turn, the player may remove a number of stones from the larger pile. The number of stones removes must be a positive multiple of the number of stones in the smaller pile.
+
+E.g., let the ordered pair (6,14) describe a configuration with 6 stones in the smaller pile and 14 stones in the larger pile, then the first player can remove 6 or 12 stones from the larger pile.
+
+The player taking all the stones from a pile wins the game.
+
+A winning configuration is one where the first player can force a win. For example, (1,5), (2,6) and (3,12) are winning configurations because the first player can immediately remove all stones in the second pile.
+
+A losing configuration is one where the second player can force a win, no matter what the first player does. For example, (2,3) and (3,4) are losing configurations: any legal move leaves a winning configuration for the second player.
+
+Define $S(N)$ as the sum of ($x_i + y_i$) for all losing configurations ($x_i$, $y_i$), $0 < x_i < y_i ≤ N$. We can verify that $S(10) = 211$ and $S({10}^4) = 230\\,312\\,207\\,313$.
+
+Find $S({10}^{16})\bmod 7^{10}$.
+
+# --hints--
+
+`stoneGameTwo()` should return `54672965`.
+
+```js
+assert.strictEqual(stoneGameTwo(), 54672965);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function stoneGameTwo() {
+
+ return true;
+}
+
+stoneGameTwo();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-326-modulo-summations.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-326-modulo-summations.md
new file mode 100644
index 00000000000..e43a4a9f23c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-326-modulo-summations.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4b21000cf542c50ffc5
+title: 'Problem 326: Modulo Summations'
+challengeType: 1
+forumTopicId: 301983
+dashedName: problem-326-modulo-summations
+---
+
+# --description--
+
+Let $a_n$ be a sequence recursively defined by: $a_1 = 1$, $\displaystyle a_n = \left(\sum_{k = 1}^{n - 1} k \times a_k\right)\bmod n$.
+
+So the first 10 elements of $a_n$ are: 1, 1, 0, 3, 0, 3, 5, 4, 1, 9.
+
+Let $f(N, M)$ represent the number of pairs $(p, q)$ such that:
+
+$$ 1 \le p \le q \le N \\; \text{and} \\; \left(\sum_{i = p}^q a_i\right)\bmod M = 0$$
+
+It can be seen that $f(10, 10) = 4$ with the pairs (3,3), (5,5), (7,9) and (9,10).
+
+You are also given that $f({10}^4, {10}^3) = 97\\,158$.
+
+Find $f({10}^{12}, {10}^6)$.
+
+# --hints--
+
+`moduloSummations()` should return `1966666166408794400`.
+
+```js
+assert.strictEqual(moduloSummations(), 1966666166408794400);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function moduloSummations() {
+
+ return true;
+}
+
+moduloSummations();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-327-rooms-of-doom.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-327-rooms-of-doom.md
new file mode 100644
index 00000000000..d324e96908a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-327-rooms-of-doom.md
@@ -0,0 +1,62 @@
+---
+id: 5900f4b31000cf542c50ffc6
+title: 'Problem 327: Rooms of Doom'
+challengeType: 1
+forumTopicId: 301984
+dashedName: problem-327-rooms-of-doom
+---
+
+# --description--
+
+A series of three rooms are connected to each other by automatic doors.
+
+
+
+Each door is operated by a security card. Once you enter a room, the door automatically closes, and that security card cannot be used again. A machine will dispense an unlimited number of cards at the start, but each room (including the starting room) contains scanners. If they detect that you are holding more than three security cards or if they detect an unattended security card on the floor, then all the doors will become permanently locked. However, each room contains a box where you may safely store any number of security cards for use at a later stage.
+
+If you simply tried to travel through the rooms one at a time then as you entered room 3 you would have used all three cards and would be trapped in that room forever!
+
+However, if you make use of the storage boxes, then escape is possible. For example, you could enter room 1 using your first card, place one card in the storage box, and use your third card to exit the room back to the start. Then after collecting three more cards from the dispensing machine you could use one to enter room 1 and collect the card you placed in the box a moment ago. You now have three cards again and will be able to travel through the remaining three doors. This method allows you to travel through all three rooms using six security cards in total.
+
+It is possible to travel through six rooms using a total of 123 security cards while carrying a maximum of 3 cards.
+
+Let $C$ be the maximum number of cards which can be carried at any time.
+
+Let $R$ be the number of rooms to travel through.
+
+Let $M(C, R)$ be the minimum number of cards required from the dispensing machine to travel through $R$ rooms carrying up to a maximum of $C$ cards at any time.
+
+For example, $M(3, 6) = 123$ and $M(4, 6) = 23$.
+
+And, $\sum M(C, 6) = 146$ for $3 ≤ C ≤ 4$.
+
+You are given that $\sum M(C, 10) = 10382$ for $3 ≤ C ≤ 10$.
+
+Find $\sum M(C, 30)$ for $3 ≤ C ≤ 40$.
+
+# --hints--
+
+`roomsOfDoom()` should return `34315549139516`.
+
+```js
+assert.strictEqual(roomsOfDoom(), 34315549139516);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function roomsOfDoom() {
+
+ return true;
+}
+
+roomsOfDoom();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-328-lowest-cost-search.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-328-lowest-cost-search.md
new file mode 100644
index 00000000000..3d3d44147e3
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-328-lowest-cost-search.md
@@ -0,0 +1,56 @@
+---
+id: 5900f4b41000cf542c50ffc7
+title: 'Problem 328: Lowest-cost Search'
+challengeType: 1
+forumTopicId: 301985
+dashedName: problem-328-lowest-cost-search
+---
+
+# --description--
+
+We are trying to find a hidden number selected from the set of integers {1, 2, ..., $n$} by asking questions. Each number (question) we ask, has a cost equal to the number asked and we get one of three possible answers:
+
+- "Your guess is lower than the hidden number", or
+- "Yes, that's it!", or
+- "Your guess is higher than the hidden number".
+
+Given the value of $n$, an optimal strategy minimizes the total cost (i.e. the sum of all the questions asked) for the worst possible case. E.g.
+
+If $n = 3$, the best we can do is obviously to ask the number "2". The answer will immediately lead us to find the hidden number (at a total cost = 2).
+
+If $n = 8$, we might decide to use a "binary search" type of strategy: Our first question would be "4" and if the hidden number is higher than 4 we will need one or two additional questions. Let our second question be "6". If the hidden number is still higher than 6, we will need a third question in order to discriminate between 7 and 8. Thus, our third question will be "7" and the total cost for this worst-case scenario will be $4 + 6 + 7 = \mathbf{\color{red}{17}}$.
+
+We can improve considerably the worst-case cost for $n = 8$, by asking "5" as our first question. If we are told that the hidden number is higher than 5, our second question will be "7", then we'll know for certain what the hidden number is (for a total cost of $5 + 7 = \mathbf{\color{blue}{12}}$). If we are told that the hidden number is lower than 5, our second question will be "3" and if the hidden number is lower than 3 our third question will be "1", giving a total cost of $5 + 3 + 1 = \mathbf{\color{blue}{9}}$. Since $\mathbf{\color{blue}{12 > 9}}$, the worst-case cost for this strategy is 12. That's better than what we achieved previously with the "binary search" strategy; it is also better than or equal to any other strategy. So, in fact, we have just described an optimal strategy for $n = 8$.
+
+Let $C(n)$ be the worst-case cost achieved by an optimal strategy for $n$, as described above. Thus $C(1) = 0$, $C(2) = 1$, $C(3) = 2$ and $C(8) = 12$.
+
+Similarly, $C(100) = 400$ and $\displaystyle\sum_{n = 1}^{100} C(n) = 17575$.
+
+Find $\displaystyle\sum_{n = 1}^{200\\,000} C(n)$.
+
+# --hints--
+
+`lowestCostSearch()` should return `260511850222`.
+
+```js
+assert.strictEqual(lowestCostSearch(), 260511850222);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function lowestCostSearch() {
+
+ return true;
+}
+
+lowestCostSearch();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-329-prime-frog.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-329-prime-frog.md
new file mode 100644
index 00000000000..e14df07e58a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-329-prime-frog.md
@@ -0,0 +1,54 @@
+---
+id: 5900f4b51000cf542c50ffc8
+title: 'Problem 329: Prime Frog'
+challengeType: 1
+forumTopicId: 301986
+dashedName: problem-329-prime-frog
+---
+
+# --description--
+
+Susan has a prime frog.
+
+Her frog is jumping around over 500 squares numbered 1 to 500.
+
+He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range [1;500]. (if it lands at either end, it automatically jumps to the only available square on the next move.)
+
+When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability $\frac{2}{3}$ or 'N' (NOT PRIME) with probability $\frac{1}{3}$ just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability $\frac{1}{3}$ or 'N' with probability $\frac{2}{3}$ just before jumping to the next square.
+
+Given that the frog's starting position is random with the same probability for every square, and given that she listens to his first 15 croaks, what is the probability that she hears the sequence PPPPNNPPPNPPNPN?
+
+Give your answer as a string as a fraction `p/q` in reduced form.
+
+# --hints--
+
+`primeFrog()` should return a string.
+
+```js
+assert(typeof primeFrog() === 'string');
+```
+
+`primeFrog()` should return the string `199740353/29386561536000`.
+
+```js
+assert.strictEqual(primeFrog(), '199740353/29386561536000');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeFrog() {
+
+ return true;
+}
+
+primeFrog();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-330-eulers-number.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-330-eulers-number.md
new file mode 100644
index 00000000000..33079aadd49
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-330-eulers-number.md
@@ -0,0 +1,54 @@
+---
+id: 5900f4b71000cf542c50ffc9
+title: 'Problem 330: Euler''s Number'
+challengeType: 1
+forumTopicId: 301988
+dashedName: problem-330-eulers-number
+---
+
+# --description--
+
+An infinite sequence of real numbers $a(n)$ is defined for all integers $n$ as follows:
+
+$$ a(n) = \begin{cases} 1 & n < 0 \\\\
+\displaystyle \sum_{i = 1}^{\infty} \frac{a(n - 1)}{i!} & n \ge 0 \end{cases} $$
+
+For example,
+
+$$\begin{align} & a(0) = \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = e − 1 \\\\
+ & a(1) = \frac{e − 1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = 2e − 3 \\\\ & a(2) = \frac{2e − 3}{1!} + \frac{e − 1}{2!} + \frac{1}{3!} + \ldots = \frac{7}{2} e − 6 \end{align}$$
+
+with $e = 2.7182818\ldots$ being Euler's constant.
+
+It can be shown that $a(n)$ is of the form $\displaystyle\frac{A(n)e + B(n)}{n!}$ for integers $A(n)$ and $B(n)$.
+
+For example $\displaystyle a(10) = \frac{328161643e − 652694486}{10!}$.
+
+Find $A({10}^9)$ + $B({10}^9)$ and give your answer $\bmod 77\\,777\\,777$.
+
+# --hints--
+
+`eulersNumber()` should return `15955822`.
+
+```js
+assert.strictEqual(eulersNumber(), 15955822);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function eulersNumber() {
+
+ return true;
+}
+
+eulersNumber();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-331-cross-flips.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-331-cross-flips.md
new file mode 100644
index 00000000000..84e5ffbdd51
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-331-cross-flips.md
@@ -0,0 +1,52 @@
+---
+id: 5900f4b71000cf542c50ffca
+title: 'Problem 331: Cross flips'
+challengeType: 1
+forumTopicId: 301989
+dashedName: problem-331-cross-flips
+---
+
+# --description--
+
+N×N disks are placed on a square game board. Each disk has a black side and white side.
+
+At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus $2 × N - 1$ disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+
+
+
+It can be proven that 3 is the minimal number of turns to finish this game.
+
+The bottom left disk on the $N×N$ board has coordinates (0, 0); the bottom right disk has coordinates ($N - 1$,$0$) and the top left disk has coordinates ($0$,$N - 1$).
+
+Let $C_N$ be the following configuration of a board with $N × N$ disks: A disk at ($x$, $y$) satisfying $N - 1 \le \sqrt{x^2 + y^2} \lt N$, shows its black side; otherwise, it shows its white side. $C_5$ is shown above.
+
+Let $T(N)$ be the minimal number of turns to finish a game starting from configuration $C_N$ or 0 if configuration $C_N$ is unsolvable. We have shown that $T(5) = 3$. You are also given that $T(10) = 29$ and $T(1\\,000) = 395\\,253$.
+
+Find $\displaystyle \sum_{i = 3}^{31} T(2^i - i)$.
+
+# --hints--
+
+`crossFlips()` should return `467178235146843500`.
+
+```js
+assert.strictEqual(crossFlips(), 467178235146843500);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function crossFlips() {
+
+ return true;
+}
+
+crossFlips();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-332-spherical-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-332-spherical-triangles.md
new file mode 100644
index 00000000000..54fe2d09a50
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-332-spherical-triangles.md
@@ -0,0 +1,52 @@
+---
+id: 5900f4b91000cf542c50ffcb
+title: 'Problem 332: Spherical triangles'
+challengeType: 1
+forumTopicId: 301990
+dashedName: problem-332-spherical-triangles
+---
+
+# --description--
+
+A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.
+
+
+
+Let $C(r)$ be the sphere with the centre (0,0,0) and radius $r$.
+
+Let $Z(r)$ be the set of points on the surface of $C(r)$ with integer coordinates.
+
+Let $T(r)$ be the set of spherical triangles with vertices in $Z(r)$. Degenerate spherical triangles, formed by three points on the same great arc, are not included in $T(r)$.
+
+Let $A(r)$ be the area of the smallest spherical triangle in $T(r)$.
+
+For example $A(14)$ is 3.294040 rounded to six decimal places.
+
+Find $\displaystyle \sum_{r = 1}^{50} A(r)$. Give your answer rounded to six decimal places.
+
+# --hints--
+
+`sphericalTriangles()` should return `2717.751525`.
+
+```js
+assert.strictEqual(sphericalTriangles(), 2717.751525);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sphericalTriangles() {
+
+ return true;
+}
+
+sphericalTriangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-333-special-partitions.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-333-special-partitions.md
new file mode 100644
index 00000000000..27cad095741
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-333-special-partitions.md
@@ -0,0 +1,53 @@
+---
+id: 5900f4b91000cf542c50ffcc
+title: 'Problem 333: Special partitions'
+challengeType: 1
+forumTopicId: 301991
+dashedName: problem-333-special-partitions
+---
+
+# --description--
+
+All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as $2^i \times 3^j$, where $i, j ≥ 0$.
+
+Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of $17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ would not be valid since 2 can divide 6. Neither would the partition $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ since 1 can divide 16. The only valid partition of 17 would be $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$.
+
+Many integers have more than one valid partition, the first being 11 having the following two partitions.
+
+$$\begin{align} & 11 = 2 + 9 = (2^1 \times 3^0 + 2^0 \times 3^2) \\\\
+ & 11 = 8 + 3 = (2^3 \times 3^0 + 2^0 \times 3^1) \end{align}$$
+
+Let's define $P(n)$ as the number of valid partitions of $n$. For example, $P(11) = 2$.
+
+Let's consider only the prime integers $q$ which would have a single valid partition such as $P(17)$.
+
+The sum of the primes $q <100$ such that $P(q) = 1$ equals 233.
+
+Find the sum of the primes $q < 1\\,000\\,000$ such that $P(q) = 1$.
+
+# --hints--
+
+`specialPartitions()` should return `3053105`.
+
+```js
+assert.strictEqual(specialPartitions(), 3053105);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function specialPartitions() {
+
+ return true;
+}
+
+specialPartitions();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-334-spilling-the-beans.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-334-spilling-the-beans.md
new file mode 100644
index 00000000000..b301ac71594
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-334-spilling-the-beans.md
@@ -0,0 +1,53 @@
+---
+id: 5900f4ba1000cf542c50ffcd
+title: 'Problem 334: Spilling the beans'
+challengeType: 1
+forumTopicId: 301992
+dashedName: problem-334-spilling-the-beans
+---
+
+# --description--
+
+In Plato's heaven, there exist an infinite number of bowls in a straight line. Each bowl either contains some or none of a finite number of beans. A child plays a game, which allows only one kind of move: removing two beans from any bowl, and putting one in each of the two adjacent bowls. The game ends when each bowl contains either one or no beans.
+
+For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:
+
+
+
+You are given the following sequences:
+
+$$\begin{align} & t_0 = 123456, \\\\
+ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ is even} \\\\
+ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ is odd} \end{cases} \\\\
+ & \qquad \text{where $⌊x⌋$ is the floor function and $\oplus$ is the bitwise XOR operator.} \\\\ & b_i = (t_i\bmod 2^{11}) + 1. \end{align}$$
+
+The first two terms of the last sequence are $b_1 = 289$ and $b_2 = 145$. If we start with $b_1$ and $b_2$ beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+
+Consider now 1500 adjacent bowls containing $b_1, b_2, \ldots, b_{1500}$ beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
+
+# --hints--
+
+`spillingTheBeans()` should return `150320021261690850`.
+
+```js
+assert.strictEqual(spillingTheBeans(), 150320021261690850);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function spillingTheBeans() {
+
+ return true;
+}
+
+spillingTheBeans();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-335-gathering-the-beans.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-335-gathering-the-beans.md
new file mode 100644
index 00000000000..c1b35177c9b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-335-gathering-the-beans.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4bd1000cf542c50ffce
+title: 'Problem 335: Gathering the beans'
+challengeType: 1
+forumTopicId: 301993
+dashedName: problem-335-gathering-the-beans
+---
+
+# --description--
+
+Whenever Peter feels bored, he places some bowls, containing one bean each, in a circle. After this, he takes all the beans out of a certain bowl and drops them one by one in the bowls going clockwise. He repeats this, starting from the bowl he dropped the last bean in, until the initial situation appears again. For example with 5 bowls he acts as follows:
+
+
+
+So with 5 bowls it takes Peter 15 moves to return to the initial situation.
+
+Let $M(x)$ represent the number of moves required to return to the initial situation, starting with $x$ bowls. Thus, $M(5) = 15$. It can also be verified that $M(100) = 10920$.
+
+Find $\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$. Give your answer modulo $7^9$.
+
+# --hints--
+
+`gatheringTheBeans()` should return `5032316`.
+
+```js
+assert.strictEqual(gatheringTheBeans(), 5032316);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function gatheringTheBeans() {
+
+ return true;
+}
+
+gatheringTheBeans();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-336-maximix-arrangements.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-336-maximix-arrangements.md
new file mode 100644
index 00000000000..c5df56c3d7b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-336-maximix-arrangements.md
@@ -0,0 +1,58 @@
+---
+id: 5900f4bd1000cf542c50ffcf
+title: 'Problem 336: Maximix Arrangements'
+challengeType: 1
+forumTopicId: 301994
+dashedName: problem-336-maximix-arrangements
+---
+
+# --description--
+
+A train is used to transport four carriages in the order: $ABCD$. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
+
+To rearrange the carriages, they are all shunted onto a large rotating turntable. After the carriages are uncoupled at a specific point, the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180°. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
+
+Some arrangements, such as $ADCB$, can be solved easily: the carriages are separated between $A$ and $D$, and after $DCB$ are rotated the correct order has been achieved.
+
+However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage $A$ in the correct place, then carriage $B$, and so on.
+
+Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are $DACB$ and $DBAC$; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for $DACB$ is shown below.
+
+
+
+It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is $DFAECB$.
+
+Find the ${2011}^{\text{th}}$ lexicographic maximix arrangement for eleven carriages.
+
+# --hints--
+
+`maximixArrangements()` should return a string.
+
+```js
+assert(typeof maximixArrangements() === 'string');
+```
+
+`maximixArrangements()` should return the string `CAGBIHEFJDK`.
+
+```js
+assert.strictEqual(maximixArrangements(), 'CAGBIHEFJDK');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function maximixArrangements() {
+
+ return true;
+}
+
+maximixArrangements();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-337-totient-stairstep-sequences.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-337-totient-stairstep-sequences.md
new file mode 100644
index 00000000000..ed090ed3f86
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-337-totient-stairstep-sequences.md
@@ -0,0 +1,52 @@
+---
+id: 5900f4be1000cf542c50ffd0
+title: 'Problem 337: Totient Stairstep Sequences'
+challengeType: 1
+forumTopicId: 301995
+dashedName: problem-337-totient-stairstep-sequences
+---
+
+# --description--
+
+Let $\\{a_1, a_2, \ldots, a_n\\}$ be an integer sequence of length $n$ such that:
+
+- $a_1 = 6$
+- for all $1 ≤ i < n$ : $φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
+
+$φ$ denotes Euler's totient function.
+
+Let $S(N)$ be the number of such sequences with $a_n ≤ N$.
+
+For example, $S(10) = 4$: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
+
+We can verify that $S(100) = 482\\,073\\,668$ and $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$.
+
+Find $S(20\\,000\\,000)\bmod {10}^8$.
+
+
+# --hints--
+
+`totientStairstepSequences()` should return `85068035`.
+
+```js
+assert.strictEqual(totientStairstepSequences(), 85068035);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function totientStairstepSequences() {
+
+ return true;
+}
+
+totientStairstepSequences();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-338-cutting-rectangular-grid-paper.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-338-cutting-rectangular-grid-paper.md
new file mode 100644
index 00000000000..9a2143b65fd
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-338-cutting-rectangular-grid-paper.md
@@ -0,0 +1,52 @@
+---
+id: 5900f4be1000cf542c50ffd1
+title: 'Problem 338: Cutting Rectangular Grid Paper'
+challengeType: 1
+forumTopicId: 301996
+dashedName: problem-338-cutting-rectangular-grid-paper
+---
+
+# --description--
+
+A rectangular sheet of grid paper with integer dimensions $w$ × $h$ is given. Its grid spacing is 1.
+
+When we cut the sheet along the grid lines into two pieces and rearrange those pieces without overlap, we can make new rectangles with different dimensions.
+
+For example, from a sheet with dimensions 9 × 4, we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
+
+
+
+Similarly, from a sheet with dimensions 9 × 8, we can make rectangles with dimensions 18 × 4 and 12 × 6.
+
+For a pair $w$ and $h$, let $F(w, h)$ be the number of distinct rectangles that can be made from a sheet with dimensions $w$ × $h$. For example, $F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$ and $F(9, 8) = 2$. Note that rectangles congruent to the initial one are not counted in $F(w, h)$. Note also that rectangles with dimensions $w$ × $h$ and dimensions $h$ × $w$ are not considered distinct.
+
+For an integer $N$, let $G(N)$ be the sum of $F(w, h)$ for all pairs $w$ and $h$ which satisfy $0 < h ≤ w ≤ N$. We can verify that $G(10) = 55$, $G({10}^3) = 971\\,745$ and $G({10}^5) = 9\\,992\\,617\\,687$.
+
+Find $G({10}^{12})$. Give your answer modulo ${10}^8$.
+
+# --hints--
+
+`cuttingRectangularGridPaper()` should return `15614292`.
+
+```js
+assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function cuttingRectangularGridPaper() {
+
+ return true;
+}
+
+cuttingRectangularGridPaper();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-339-peredur-fab-efrawg.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-339-peredur-fab-efrawg.md
new file mode 100644
index 00000000000..7c1934c581b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-339-peredur-fab-efrawg.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4c01000cf542c50ffd2
+title: 'Problem 339: Peredur fab Efrawg'
+challengeType: 1
+forumTopicId: 301997
+dashedName: problem-339-peredur-fab-efrawg
+---
+
+# --description--
+
+"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black." - Peredur the Son of Evrawc
+
+Initially, each flock consists of $n$ sheep. Each sheep (regardless of color) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let $E(n)$ be the expected final number of black sheep if Peredur uses an optimal strategy.
+
+You are given that $E(5) = 6.871346$ rounded to 6 places behind the decimal point.
+
+Find $E(10\\,000)$ and give your answer rounded to 6 places behind the decimal point.
+
+# --hints--
+
+`peredurFabEfrawg()` should return `19823.542204`.
+
+```js
+assert.strictEqual(peredurFabEfrawg(), 19823.542204);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function peredurFabEfrawg() {
+
+ return true;
+}
+
+peredurFabEfrawg();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-340-crazy-function.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-340-crazy-function.md
new file mode 100644
index 00000000000..72da02c1095
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-340-crazy-function.md
@@ -0,0 +1,47 @@
+---
+id: 5900f4c21000cf542c50ffd4
+title: 'Problem 340: Crazy Function'
+challengeType: 1
+forumTopicId: 301999
+dashedName: problem-340-crazy-function
+---
+
+# --description--
+
+For fixed integers $a$, $b$, $c$, define the crazy function $F(n)$ as follows:
+
+$$\begin{align} & F(n) = n - c \\;\text{ for all } n > b \\\\
+ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ for all } n ≤ b. \end{align}$$
+
+Also, define $S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$.
+
+For example, if $a = 50$, $b = 2000$ and $c = 40$, then $F(0) = 3240$ and $F(2000) = 2040$. Also, $S(50, 2000, 40) = 5\\,204\\,240$.
+
+Find the last 9 digits of $S({21}^7, 7^{21}, {12}^7)$.
+
+# --hints--
+
+`crazyFunction()` should return `291504964`.
+
+```js
+assert.strictEqual(crazyFunction(), 291504964);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function crazyFunction() {
+
+ return true;
+}
+
+crazyFunction();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-341-golombs-self-describing-sequence.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-341-golombs-self-describing-sequence.md
new file mode 100644
index 00000000000..f3ebbd9cdd0
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-341-golombs-self-describing-sequence.md
@@ -0,0 +1,47 @@
+---
+id: 5900f4c11000cf542c50ffd3
+title: 'Problem 341: Golomb''s self-describing sequence'
+challengeType: 1
+forumTopicId: 302000
+dashedName: problem-341-golombs-self-describing-sequence
+---
+
+# --description--
+
+The Golomb's self-describing sequence ($G(n)$) is the only nondecreasing sequence of natural numbers such that $n$ appears exactly $G(n)$ times in the sequence. The values of $G(n)$ for the first few $n$ are
+
+$$\begin{array}{c} n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & \ldots \\\\
+ G(n) & 1 & 2 & 2 & 3 & 3 & 4 & 4 & 4 & 5 & 5 & 5 & 6 & 6 & 6 & 6 & \ldots \end{array}$$
+
+You are given that $G({10}^3) = 86$, $G({10}^6) = 6137$.
+
+You are also given that $\sum G(n^3) = 153\\,506\\,976$ for $1 ≤ n < {10}^3$.
+
+Find $\sum G(n^3)$ for $1 ≤ n < {10}^6$.
+
+# --hints--
+
+`golombsSequence()` should return `56098610614277016`.
+
+```js
+assert.strictEqual(golombsSequence(), 56098610614277016);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function golombsSequence() {
+
+ return true;
+}
+
+golombsSequence();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-342-the-totient-of-a-square-is-a-cube.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-342-the-totient-of-a-square-is-a-cube.md
new file mode 100644
index 00000000000..85990bc5b54
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-342-the-totient-of-a-square-is-a-cube.md
@@ -0,0 +1,45 @@
+---
+id: 5900f4c31000cf542c50ffd5
+title: 'Problem 342: The totient of a square is a cube'
+challengeType: 1
+forumTopicId: 302001
+dashedName: problem-342-the-totient-of-a-square-is-a-cube
+---
+
+# --description--
+
+Consider the number 50.
+
+${50}^2 = 2500 = 2^2 × 5^4$, so $φ(2500) = 2 × 4 × 5^3 = 8 × 5^3 = 2^3 × 5^3$. $φ$ denotes Euler's totient function.
+
+So 2500 is a square and $φ(2500)$ is a cube.
+
+Find the sum of all numbers $n$, $1 < n < {10}^{10}$ such that $φ(n^2)$ is a cube.
+
+
+# --hints--
+
+`totientOfSquare()` should return `5943040885644`.
+
+```js
+assert.strictEqual(totientOfSquare(), 5943040885644);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function totientOfSquare() {
+
+ return true;
+}
+
+totientOfSquare();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-343-fractional-sequences.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-343-fractional-sequences.md
new file mode 100644
index 00000000000..f284af9e94b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-343-fractional-sequences.md
@@ -0,0 +1,55 @@
+---
+id: 5900f4c41000cf542c50ffd6
+title: 'Problem 343: Fractional Sequences'
+challengeType: 1
+forumTopicId: 302002
+dashedName: problem-343-fractional-sequences
+---
+
+# --description--
+
+For any positive integer $k$, a finite sequence $a_i$ of fractions $\frac{x_i}{y_i}$ is defined by:
+
+- $a_1 = \displaystyle\frac{1}{k}$ and
+- $a_i = \displaystyle\frac{(x_{i - 1} + 1)}{(y_{i - 1} - 1)}$ reduced to lowest terms for $i > 1$.
+
+When $a_i$ reaches some integer $n$, the sequence stops. (That is, when $y_i = 1$.)
+
+Define $f(k) = n$.
+
+For example, for $k = 20$:
+
+$$\frac{1}{20} → \frac{2}{19} → \frac{3}{18} = \frac{1}{6} → \frac{2}{5} → \frac{3}{4} → \frac{4}{3} → \frac{5}{2} → \frac{6}{1} = 6$$
+
+So $f(20) = 6$.
+
+Also $f(1) = 1$, $f(2) = 2$, $f(3) = 1$ and $\sum f(k^3) = 118\\,937$ for $1 ≤ k ≤ 100$.
+
+Find $\sum f(k^3)$ for $1 ≤ k ≤ 2 × {10}^6$.
+
+# --hints--
+
+`fractionalSequences()` should return `269533451410884200`.
+
+```js
+assert.strictEqual(fractionalSequences(), 269533451410884200);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function fractionalSequences() {
+
+ return true;
+}
+
+fractionalSequences();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-344-silver-dollar-game.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-344-silver-dollar-game.md
new file mode 100644
index 00000000000..0f9fcc5f2e6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-344-silver-dollar-game.md
@@ -0,0 +1,56 @@
+---
+id: 5900f4c51000cf542c50ffd7
+title: 'Problem 344: Silver dollar game'
+challengeType: 1
+forumTopicId: 302003
+dashedName: problem-344-silver-dollar-game
+---
+
+# --description--
+
+One variant of N.G. de Bruijn's silver dollar game can be described as follows:
+
+On a strip of squares a number of coins are placed, at most one coin per square. Only one coin, called the silver dollar, has any value. Two players take turns making moves. At each turn a player must make either a regular or a special move.
+
+A regular move consists of selecting one coin and moving it one or more squares to the left. The coin cannot move out of the strip or jump on or over another coin.
+
+Alternatively, the player can choose to make the special move of pocketing the leftmost coin rather than making a regular move. If no regular moves are possible, the player is forced to pocket the leftmost coin.
+
+The winner is the player who pockets the silver dollar.
+
+
+
+A winning configuration is an arrangement of coins on the strip where the first player can force a win no matter what the second player does.
+
+Let $W(n, c)$ be the number of winning configurations for a strip of $n$ squares, $c$ worthless coins and one silver dollar.
+
+You are given that $W(10, 2) = 324$ and $W(100, 10) = 1\\,514\\,704\\,946\\,113\\,500$.
+
+Find $W(1\\,000\\,000, 100)$ modulo the semiprime $1000\\,036\\,000\\,099 (= 1\\,000\\,003 \times 1\\,000\\,033)$.
+
+# --hints--
+
+`silverDollarGame()` should return `65579304332`.
+
+```js
+assert.strictEqual(silverDollarGame(), 65579304332);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function silverDollarGame() {
+
+ return true;
+}
+
+silverDollarGame();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-345-matrix-sum.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-345-matrix-sum.md
new file mode 100644
index 00000000000..19aa26fd74f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-345-matrix-sum.md
@@ -0,0 +1,55 @@
+---
+id: 5900f4c81000cf542c50ffda
+title: 'Problem 345: Matrix Sum'
+challengeType: 1
+forumTopicId: 302004
+dashedName: problem-345-matrix-sum
+---
+
+# --description--
+
+We define the Matrix Sum of a matrix as the maximum sum of matrix elements with each element being the only one in his row and column.
+
+For example, the Matrix Sum of the matrix below equals $3315 ( = 863 + 383 + 343 + 959 + 767)$:
+
+$$\begin{array}{rrrrr} 7 & 53 & 183 & 439 & \color{lime}{863} \\\\
+ 497 & \color{lime}{383} & 563 & 79 & 973 \\\\ 287 & 63 & \color{lime}{343} & 169 & 583 \\\\
+ 627 & 343 & 773 & \color{lime}{959} & 943 \\\\ \color{lime}{767} & 473 & 103 & 699 & 303 \end{array}$$
+
+Find the Matrix Sum of:
+
+$$\\begin{array}{r} 7 & 53 & 183 & 439 & 863 & 497 & 383 & 563 & 79 & 973 & 287 & 63 & 343 & 169 & 583 \\\\
+ 627 & 343 & 773 & 959 & 943 & 767 & 473 & 103 & 699 & 303 & 957 & 703 & 583 & 639 & 913 \\\\ 447 & 283 & 463 & 29 & 23 & 487 & 463 & 993 & 119 & 883 & 327 & 493 & 423 & 159 & 743 \\\\
+ 217 & 623 & 3 & 399 & 853 & 407 & 103 & 983 & 89 & 463 & 290 & 516 & 212 & 462 & 350 \\\\ 960 & 376 & 682 & 962 & 300 & 780 & 486 & 502 & 912 & 800 & 250 & 346 & 172 & 812 & 350 \\\\
+ 870 & 456 & 192 & 162 & 593 & 473 & 915 & 45 & 989 & 873 & 823 & 965 & 425 & 329 & 803 \\\\ 973 & 965 & 905 & 919 & 133 & 673 & 665 & 235 & 509 & 613 & 673 & 815 & 165 & 992 & 326 \\\\
+ 322 & 148 & 972 & 962 & 286 & 255 & 941 & 541 & 265 & 323 & 925 & 281 & 601 & 95 & 973 \\\\ 445 & 721 & 11 & 525 & 473 & 65 & 511 & 164 & 138 & 672 & 18 & 428 & 154 & 448 & 848 \\\\
+ 414 & 456 & 310 & 312 & 798 & 104 & 566 & 520 & 302 & 248 & 694 & 976 & 430 & 392 & 198 \\\\ 184 & 829 & 373 & 181 & 631 & 101 & 969 & 613 & 840 & 740 & 778 & 458 & 284 & 760 & 390 \\\\
+ 821 & 461 & 843 & 513 & 17 & 901 & 711 & 993 & 293 & 157 & 274 & 94 & 192 & 156 & 574 \\\\ 34 & 124 & 4 & 878 & 450 & 476 & 712 & 914 & 838 & 669 & 875 & 299 & 823 & 329 & 699 \\\\
+ 815 & 559 & 813 & 459 & 522 & 788 & 168 & 586 & 966 & 232 & 308 & 833 & 251 & 631 & 107 \\\\ 813 & 883 & 451 & 509 & 615 & 77 & 281 & 613 & 459 & 205 & 380 & 274 & 302 & 35 & 805 \end{array}$$
+
+# --hints--
+
+`matrixSum()` should return `13938`.
+
+```js
+assert.strictEqual(matrixSum(), 13938);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function matrixSum() {
+
+ return true;
+}
+
+matrixSum();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-346-strong-repunits.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-346-strong-repunits.md
new file mode 100644
index 00000000000..98b7cc48b2f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-346-strong-repunits.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4c71000cf542c50ffd8
+title: 'Problem 346: Strong Repunits'
+challengeType: 1
+forumTopicId: 302005
+dashedName: problem-346-strong-repunits
+---
+
+# --description--
+
+The number 7 is special, because 7 is 111 written in base 2, and 11 written in base 6 (i.e. $7_{10} = {11}_6 = {111}_2$). In other words, 7 is a repunit in at least two bases $b > 1$.
+
+We shall call a positive integer with this property a strong repunit. It can be verified that there are 8 strong repunits below 50: {1, 7, 13, 15, 21, 31, 40, 43}. Furthermore, the sum of all strong repunits below 1000 equals 15864.
+
+Find the sum of all strong repunits below ${10}^{12}$.
+
+# --hints--
+
+`strongRepunits()` should return `336108797689259260`.
+
+```js
+assert.strictEqual(strongRepunits(), 336108797689259260);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function strongRepunits() {
+
+ return true;
+}
+
+strongRepunits();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-347-largest-integer-divisible-by-two-primes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-347-largest-integer-divisible-by-two-primes.md
new file mode 100644
index 00000000000..15174e82655
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-347-largest-integer-divisible-by-two-primes.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4c81000cf542c50ffd9
+title: 'Problem 347: Largest integer divisible by two primes'
+challengeType: 1
+forumTopicId: 302006
+dashedName: problem-347-largest-integer-divisible-by-two-primes
+---
+
+# --description--
+
+The largest integer $≤ 100$ that is only divisible by both the primes 2 and 3 is 96, as $96 = 32 \times 3 = 2^5 \times 3$.
+
+For two distinct primes $p$ and $q$ let $M(p, q, N)$ be the largest positive integer $≤ N$ only divisible by both $p$ and $q$ and $M(p, q, N)=0$ if such a positive integer does not exist.
+
+E.g. $M(2, 3, 100) = 96$.
+
+$M(3, 5, 100) = 75$ and not 90 because 90 is divisible by 2, 3 and 5. Also $M(2, 73, 100) = 0$ because there does not exist a positive integer $≤ 100$ that is divisible by both 2 and 73.
+
+Let $S(N)$ be the sum of all distinct $M(p, q, N)$. $S(100)=2262$.
+
+Find $S(10\\,000\\,000)$.
+
+# --hints--
+
+`integerDivisibleByTwoPrimes()` should return `11109800204052`.
+
+```js
+assert.strictEqual(integerDivisibleByTwoPrimes(), 11109800204052);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function integerDivisibleByTwoPrimes() {
+
+ return true;
+}
+
+integerDivisibleByTwoPrimes();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-348-sum-of-a-square-and-a-cube.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-348-sum-of-a-square-and-a-cube.md
new file mode 100644
index 00000000000..8e69b16ca7a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-348-sum-of-a-square-and-a-cube.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4c81000cf542c50ffdb
+title: 'Problem 348: Sum of a square and a cube'
+challengeType: 1
+forumTopicId: 302007
+dashedName: problem-348-sum-of-a-square-and-a-cube
+---
+
+# --description--
+
+Many numbers can be expressed as the sum of a square and a cube. Some of them in more than one way.
+
+Consider the palindromic numbers that can be expressed as the sum of a square and a cube, both greater than 1, in exactly 4 different ways.
+
+For example, 5229225 is a palindromic number and it can be expressed in exactly 4 different ways:
+
+$$\begin{align} & {2285}^2 + {20}^3 \\\\
+ & {2223}^2 + {66}^3 \\\\ & {1810}^2 + {125}^3 \\\\
+ & {1197}^2 + {156}^3 \end{align}$$
+
+Find the sum of the five smallest such palindromic numbers.
+
+# --hints--
+
+`sumOfSquareAndCube()` should return `1004195061`.
+
+```js
+assert.strictEqual(sumOfSquareAndCube(), 1004195061);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumOfSquareAndCube() {
+
+ return true;
+}
+
+sumOfSquareAndCube();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-349-langtons-ant.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-349-langtons-ant.md
new file mode 100644
index 00000000000..71fe17860a2
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-349-langtons-ant.md
@@ -0,0 +1,45 @@
+---
+id: 5900f4ca1000cf542c50ffdc
+title: 'Problem 349: Langton''s ant'
+challengeType: 1
+forumTopicId: 302008
+dashedName: problem-349-langtons-ant
+---
+
+# --description--
+
+An ant moves on a regular grid of squares that are coloured either black or white.
+
+The ant is always oriented in one of the cardinal directions (left, right, up or down) and moves from square to adjacent square according to the following rules:
+
+- if it is on a black square, it flips the color of the square to white, rotates 90° counterclockwise and moves forward one square.
+- if it is on a white square, it flips the color of the square to black, rotates 90° clockwise and moves forward one square.
+
+Starting with a grid that is entirely white, how many squares are black after ${10}^{18}$ moves of the ant?
+
+# --hints--
+
+`langtonsAnt()` should return `115384615384614940`.
+
+```js
+assert.strictEqual(langtonsAnt(), 115384615384614940);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function langtonsAnt() {
+
+ return true;
+}
+
+langtonsAnt();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-350-constraining-the-least-greatest-and-the-greatest-least.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
new file mode 100644
index 00000000000..b40eb3cd67a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4cb1000cf542c50ffdd
+title: 'Problem 350: Constraining the least greatest and the greatest least'
+challengeType: 1
+forumTopicId: 302010
+dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
+---
+
+# --description--
+
+A list of size $n$ is a sequence of $n$ natural numbers. Examples are (2, 4, 6), (2, 6, 4), (10, 6, 15, 6), and (11).
+
+The greatest common divisor, or $gcd$, of a list is the largest natural number that divides all entries of the list. Examples: $gcd(2, 6, 4) = 2$, $gcd(10, 6, 15, 6) = 1$ and $gcd(11) = 11$.
+
+The least common multiple, or $lcm$, of a list is the smallest natural number divisible by each entry of the list. Examples: $lcm(2, 6, 4) = 12$, $lcm(10, 6, 15, 6) = 30$ and $lcm(11) = 11$.
+
+Let $f(G, L, N)$ be the number of lists of size $N$ with $gcd ≥ G$ and $lcm ≤ L$. For example:
+
+$$\begin{align} & f(10, 100, 1) = 91 \\\\
+ & f(10, 100, 2) = 327 \\\\ & f(10, 100, 3) = 1135 \\\\
+ & f(10, 100, 1000)\bmod {101}^4 = 3\\,286\\,053 \end{align}$$
+
+Find $f({10}^6, {10}^{12}, {10}^{18})\bmod {101}^4$.
+
+# --hints--
+
+`leastGreatestAndGreatestLeast()` should return `84664213`.
+
+```js
+assert.strictEqual(leastGreatestAndGreatestLeast(), 84664213);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function leastGreatestAndGreatestLeast() {
+
+ return true;
+}
+
+leastGreatestAndGreatestLeast();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-351-hexagonal-orchards.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-351-hexagonal-orchards.md
new file mode 100644
index 00000000000..fa6811e9185
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-351-hexagonal-orchards.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4cb1000cf542c50ffde
+title: 'Problem 351: Hexagonal orchards'
+challengeType: 1
+forumTopicId: 302011
+dashedName: problem-351-hexagonal-orchards
+---
+
+# --description--
+
+A hexagonal orchard of order $n$ is a triangular lattice made up of points within a regular hexagon with side $n$. The following is an example of a hexagonal orchard of order 5:
+
+
+
+Highlighted in green are the points which are hidden from the center by a point closer to it. It can be seen that for a hexagonal orchard of order 5, 30 points are hidden from the center.
+
+Let $H(n)$ be the number of points hidden from the center in a hexagonal orchard of order $n$.
+
+$H(5) = 30$. $H(10) = 138$. $H(1\\,000)$ = $1\\,177\\,848$.
+
+Find $H(100\\,000\\,000)$.
+
+# --hints--
+
+`hexagonalOrchards()` should return `11762187201804552`.
+
+```js
+assert.strictEqual(hexagonalOrchards(), 11762187201804552);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function hexagonalOrchards() {
+
+ return true;
+}
+
+hexagonalOrchards();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-352-blood-tests.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-352-blood-tests.md
new file mode 100644
index 00000000000..b0de4ec7213
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-352-blood-tests.md
@@ -0,0 +1,70 @@
+---
+id: 5900f4cd1000cf542c50ffdf
+title: 'Problem 352: Blood tests'
+challengeType: 1
+forumTopicId: 302012
+dashedName: problem-352-blood-tests
+---
+
+# --description--
+
+Each one of the 25 sheep in a flock must be tested for a rare virus, known to affect 2% of the sheep population.
+
+An accurate and extremely sensitive PCR test exists for blood samples, producing a clear positive / negative result, but it is very time-consuming and expensive.
+
+Because of the high cost, the vet-in-charge suggests that instead of performing 25 separate tests, the following procedure can be used instead:
+
+The sheep are split into 5 groups of 5 sheep in each group. For each group, the 5 samples are mixed together and a single test is performed. Then,
+
+- If the result is negative, all the sheep in that group are deemed to be virus-free.
+- If the result is positive, 5 additional tests will be performed (a separate test for each animal) to determine the affected individual(s).
+
+Since the probability of infection for any specific animal is only 0.02, the first test (on the pooled samples) for each group will be:
+
+- Negative (and no more tests needed) with probability ${0.98}^5 = 0.9039207968$.
+- Positive (5 additional tests needed) with probability $1 - 0.9039207968 = 0.0960792032$.
+
+Thus, the expected number of tests for each group is $1 + 0.0960792032 × 5 = 1.480396016$.
+
+Consequently, all 5 groups can be screened using an average of only $1.480396016 × 5 = \mathbf{7.40198008}$ tests, which represents a huge saving of more than 70%!
+
+Although the scheme we have just described seems to be very efficient, it can still be improved considerably (always assuming that the test is sufficiently sensitive and no adverse effects are caused by mixing different samples). E.g.:
+
+- We may start by running a test on a mixture of all the 25 samples. It can be verified that in about 60.35% of the cases this test will be negative, thus no more tests will be needed. Further testing will only be required for the remaining 39.65% of the cases.
+- If we know that at least one animal in a group of 5 is infected and the first 4 individual tests come out negative, there is no need to run a test on the fifth animal (we know that it must be infected).
+- We can try a different number of groups / different number of animals in each group, adjusting those numbers at each level so that the total expected number of tests will be minimised.
+
+To simplify the very wide range of possibilities, there is one restriction we place when devising the most cost-efficient testing scheme: whenever we start with a mixed sample, all the sheep contributing to that sample must be fully screened (i.e. a verdict of infected / virus-free must be reached for all of them) before we start examining any other animals.
+
+For the current example, it turns out that the most cost-efficient testing scheme (we'll call it the optimal strategy) requires an average of just 4.155452 tests!
+
+Using the optimal strategy, let $T(s, p)$ represent the average number of tests needed to screen a flock of $s$ sheep for a virus having probability $p$ to be present in any individual. Thus, rounded to six decimal places, $T(25, 0.02) = 4.155452$ and $T(25, 0.10) = 12.702124$.
+
+Find $\sum T(10\\,000, p)$ for $p = 0.01, 0.02, 0.03, \ldots 0.50$. Give your answer rounded to six decimal places.
+
+# --hints--
+
+`bloodTests()` should return `378563.260589`.
+
+```js
+assert.strictEqual(bloodTests(), 378563.260589);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function bloodTests() {
+
+ return true;
+}
+
+bloodTests();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-353-risky-moon.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-353-risky-moon.md
new file mode 100644
index 00000000000..83cb0d40c9e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-353-risky-moon.md
@@ -0,0 +1,54 @@
+---
+id: 5900f4cd1000cf542c50ffe0
+title: 'Problem 353: Risky moon'
+challengeType: 1
+forumTopicId: 302013
+dashedName: problem-353-risky-moon
+---
+
+# --description--
+
+A moon could be described by the sphere $C(r)$ with centre (0, 0, 0) and radius $r$.
+
+There are stations on the moon at the points on the surface of $C(r)$ with integer coordinates. The station at (0, 0, $r$) is called North Pole station, the station at (0, 0, $-r$) is called South Pole station.
+
+All stations are connected with each other via the shortest road on the great arc through the stations. A journey between two stations is risky. If $d$ is the length of the road between two stations, $\{\left(\frac{d}{πr}\right)}^2$ is a measure for the risk of the journey (let us call it the risk of the road). If the journey includes more than two stations, the risk of the journey is the sum of risks of the used roads.
+
+A direct journey from the North Pole station to the South Pole station has the length $πr$ and risk 1. The journey from the North Pole station to the South Pole station via (0, $r$, 0) has the same length, but a smaller risk:
+
+$${\left(\frac{\frac{1}{2}πr}{πr}\right)}^2+{\left(\frac{\frac{1}{2}πr}{πr}\right)}^2 = 0.5$$
+
+The minimal risk of a journey from the North Pole station to the South Pole station on $C(r)$ is $M(r)$.
+
+You are given that $M(7) = 0.178\\,494\\,399\\,8$ rounded to 10 digits behind the decimal point.
+
+Find $\displaystyle\sum_{n = 1}^{15} M(2^n - 1)$.
+
+Give your answer rounded to 10 digits behind the decimal point in the form a.bcdefghijk.
+
+# --hints--
+
+`riskyMoon()` should return `1.2759860331`.
+
+```js
+assert.strictEqual(riskyMoon(), 1.2759860331);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function riskyMoon() {
+
+ return true;
+}
+
+riskyMoon();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-354-distances-in-a-bees-honeycomb.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-354-distances-in-a-bees-honeycomb.md
new file mode 100644
index 00000000000..f7d023146ca
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-354-distances-in-a-bees-honeycomb.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4cf1000cf542c50ffe1
+title: 'Problem 354: Distances in a bee''s honeycomb'
+challengeType: 1
+forumTopicId: 302014
+dashedName: problem-354-distances-in-a-bees-honeycomb
+---
+
+# --description--
+
+Consider a honey bee's honeycomb where each cell is a perfect regular hexagon with side length 1.
+
+
+
+One particular cell is occupied by the queen bee. For a positive real number $L$, let $B(L)$ count the cells with distance $L$ from the queen bee cell (all distances are measured from centre to centre); you may assume that the honeycomb is large enough to accommodate for any distance we wish to consider.
+
+For example, $B(\sqrt{3}) = 6$, $B(\sqrt{21}) = 12$ and $B(111\\,111\\,111) = 54$.
+
+Find the number of $L ≤ 5 \times {10}^{11}$ such that $B(L) = 450$.
+
+# --hints--
+
+`distancesInHoneycomb()` should return `58065134`.
+
+```js
+assert.strictEqual(distancesInHoneycomb(), 58065134);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function distancesInHoneycomb() {
+
+ return true;
+}
+
+distancesInHoneycomb();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-355-maximal-coprime-subset.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-355-maximal-coprime-subset.md
new file mode 100644
index 00000000000..a7e2179ec87
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-355-maximal-coprime-subset.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4d01000cf542c50ffe2
+title: 'Problem 355: Maximal coprime subset'
+challengeType: 1
+forumTopicId: 302015
+dashedName: problem-355-maximal-coprime-subset
+---
+
+# --description--
+
+Define $Co(n)$ to be the maximal possible sum of a set of mutually co-prime elements from $\\{1, 2, \ldots, n\\}$. For example $Co(10)$ is 30 and hits that maximum on the subset $\\{1, 5, 7, 8, 9\\}$.
+
+You are given that $Co(30) = 193$ and $Co(100) = 1356$.
+
+Find $Co(200\\,000)$.
+
+# --hints--
+
+`maximalCoprimeSubset()` should return `1726545007`.
+
+```js
+assert.strictEqual(maximalCoprimeSubset(), 1726545007);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function maximalCoprimeSubset() {
+
+ return true;
+}
+
+maximalCoprimeSubset();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-356-largest-roots-of-cubic-polynomials.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-356-largest-roots-of-cubic-polynomials.md
new file mode 100644
index 00000000000..ec4939b68f1
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-356-largest-roots-of-cubic-polynomials.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4d01000cf542c50ffe3
+title: 'Problem 356: Largest roots of cubic polynomials'
+challengeType: 1
+forumTopicId: 302016
+dashedName: problem-356-largest-roots-of-cubic-polynomials
+---
+
+# --description--
+
+Let $a_n$ be the largest real root of a polynomial $g(x) = x^3 - 2^n \times x^2 + n$.
+
+For example, $a_2 = 3.86619826\ldots$
+
+Find the last eight digits of $\displaystyle\sum_{i = 1}^{30} \lfloor {a_i}^{987654321}\rfloor$.
+
+**Note:** $\lfloor a\rfloor$ represents the floor function.
+
+# --hints--
+
+`rootsOfCubicPolynomials()` should return `28010159`.
+
+```js
+assert.strictEqual(rootsOfCubicPolynomials(), 28010159);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function rootsOfCubicPolynomials() {
+
+ return true;
+}
+
+rootsOfCubicPolynomials();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-357-prime-generating-integers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-357-prime-generating-integers.md
new file mode 100644
index 00000000000..003fc35bdd6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-357-prime-generating-integers.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4d11000cf542c50ffe4
+title: 'Problem 357: Prime generating integers'
+challengeType: 1
+forumTopicId: 302017
+dashedName: problem-357-prime-generating-integers
+---
+
+# --description--
+
+Consider the divisors of 30: 1, 2, 3, 5, 6, 10, 15, 30.
+
+It can be seen that for every divisor $d$ of 30, $d + \frac{30}{d}$ is prime.
+
+Find the sum of all positive integers $n$ not exceeding $100\\,000\\,000$ such that for every divisor $d$ of $n$, $d + \frac{n}{d}$ is prime.
+
+# --hints--
+
+`primeGeneratingIntegers()` should return `1739023853137`.
+
+```js
+assert.strictEqual(primeGeneratingIntegers(), 1739023853137);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeGeneratingIntegers() {
+
+ return true;
+}
+
+primeGeneratingIntegers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-358-cyclic-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-358-cyclic-numbers.md
new file mode 100644
index 00000000000..9a7f94d3bff
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-358-cyclic-numbers.md
@@ -0,0 +1,57 @@
+---
+id: 5900f4d21000cf542c50ffe5
+title: 'Problem 358: Cyclic numbers'
+challengeType: 1
+forumTopicId: 302018
+dashedName: problem-358-cyclic-numbers
+---
+
+# --description--
+
+A cyclic number with $n$ digits has a very interesting property:
+
+When it is multiplied by 1, 2, 3, 4, ... $n$, all the products have exactly the same digits, in the same order, but rotated in a circular fashion!
+
+The smallest cyclic number is the 6-digit number 142857:
+
+$$\begin{align} & 142857 × 1 = 142857 \\\\
+ & 142857 × 2 = 285714 \\\\ & 142857 × 3 = 428571 \\\\
+ & 142857 × 4 = 571428 \\\\ & 142857 × 5 = 714285 \\\\
+ & 142857 × 6 = 857142 \end{align}$$
+
+The next cyclic number is 0588235294117647 with 16 digits:
+
+$$\begin{align} & 0588235294117647 × 1 = 0588235294117647 \\\\
+ & 0588235294117647 × 2 = 1176470588235294 \\\\ & 0588235294117647 × 3 = 1764705882352941 \\\\
+ & \ldots \\\\ & 0588235294117647 × 16 = 9411764705882352 \end{align}$$
+
+Note that for cyclic numbers, leading zeros are important.
+
+There is only one cyclic number for which, the eleven leftmost digits are 00000000137 and the five rightmost digits are 56789 (i.e., it has the form $00000000137\ldots56789$ with an unknown number of digits in the middle). Find the sum of all its digits.
+
+# --hints--
+
+`cyclicNumbers()` should return `3284144505`.
+
+```js
+assert.strictEqual(cyclicNumbers(), 3284144505);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function cyclicNumbers() {
+
+ return true;
+}
+
+cyclicNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-359-hilberts-new-hotel.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-359-hilberts-new-hotel.md
new file mode 100644
index 00000000000..0cfd6a75f09
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-359-hilberts-new-hotel.md
@@ -0,0 +1,62 @@
+---
+id: 5900f4d31000cf542c50ffe6
+title: 'Problem 359: Hilbert''s New Hotel'
+challengeType: 1
+forumTopicId: 302019
+dashedName: problem-359-hilberts-new-hotel
+---
+
+# --description--
+
+An infinite number of people (numbered 1, 2, 3, etc.) are lined up to get a room at Hilbert's newest infinite hotel. The hotel contains an infinite number of floors (numbered 1, 2, 3, etc.), and each floor contains an infinite number of rooms (numbered 1, 2, 3, etc.).
+
+Initially the hotel is empty. Hilbert declares a rule on how the $n^{\text{th}}$ person is assigned a room: person $n$ gets the first vacant room in the lowest numbered floor satisfying either of the following:
+
+- the floor is empty
+- the floor is not empty, and if the latest person taking a room in that floor is person $m$, then $m + n$ is a perfect square
+
+Person 1 gets room 1 in floor 1 since floor 1 is empty.
+
+Person 2 does not get room 2 in floor 1 since 1 + 2 = 3 is not a perfect square.
+
+Person 2 instead gets room 1 in floor 2 since floor 2 is empty.
+
+Person 3 gets room 2 in floor 1 since 1 + 3 = 4 is a perfect square.
+
+Eventually, every person in the line gets a room in the hotel.
+
+Define $P(f, r)$ to be $n$ if person $n$ occupies room $r$ in floor $f$, and 0 if no person occupies the room. Here are a few examples:
+
+$$\begin{align} & P(1, 1) = 1 \\\\
+ & P(1, 2) = 3 \\\\ & P(2, 1) = 2 \\\\
+ & P(10, 20) = 440 \\\\ & P(25, 75) = 4863 \\\\
+ & P(99, 100) = 19454 \end{align}$$
+
+Find the sum of all $P(f, r)$ for all positive $f$ and $r$ such that $f × r = 71\\,328\\,803\\,586\\,048$ and give the last 8 digits as your answer.
+
+# --hints--
+
+`hilbertsNewHotel()` should return `40632119`.
+
+```js
+assert.strictEqual(hilbertsNewHotel(), 40632119);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function hilbertsNewHotel() {
+
+ return true;
+}
+
+hilbertsNewHotel();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-360-scary-sphere.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-360-scary-sphere.md
new file mode 100644
index 00000000000..932a0a9dc4e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-360-scary-sphere.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4d41000cf542c50ffe7
+title: 'Problem 360: Scary Sphere'
+challengeType: 1
+forumTopicId: 302021
+dashedName: problem-360-scary-sphere
+---
+
+# --description--
+
+Given two points ($x_1$, $y_1$, $z_1$) and ($x_2$, $y_2$, $z_2$) in three dimensional space, the Manhattan distance between those points is defined as $|x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2|$.
+
+Let $C(r)$ be a sphere with radius $r$ and center in the origin $O(0, 0, 0)$.
+
+Let $I(r)$ be the set of all points with integer coordinates on the surface of $C(r)$.
+
+Let $S(r)$ be the sum of the Manhattan distances of all elements of $I(r)$ to the origin $O$.
+
+E.g. $S(45)=34518$.
+
+Find $S({10}^{10})$.
+
+# --hints--
+
+`scarySphere()` should return `878825614395267100`.
+
+```js
+assert.strictEqual(scarySphere(), 878825614395267100);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function scarySphere() {
+
+ return true;
+}
+
+scarySphere();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-361-subsequence-of-thue-morse-sequence.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-361-subsequence-of-thue-morse-sequence.md
new file mode 100644
index 00000000000..efae1fb220c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-361-subsequence-of-thue-morse-sequence.md
@@ -0,0 +1,55 @@
+---
+id: 5900f4d51000cf542c50ffe8
+title: 'Problem 361: Subsequence of Thue-Morse sequence'
+challengeType: 1
+forumTopicId: 302022
+dashedName: problem-361-subsequence-of-thue-morse-sequence
+---
+
+# --description--
+
+The Thue-Morse sequence $\\{T_n\\}$ is a binary sequence satisfying:
+
+- $T_0 = 0$
+- $T_{2n} = T_n$
+- $T_{2n + 1} = 1 - T_n$
+
+The first several terms of $\\{T_n\\}$ are given as follows: $01101001\color{red}{10010}1101001011001101001\ldots$.
+
+We define $\\{A_n\\}$ as the sorted sequence of integers such that the binary expression of each element appears as a subsequence in $\\{T_n\\}$. For example, the decimal number 18 is expressed as 10010 in binary. 10010 appears in $\\{T_n\\}$ ($T_8$ to $T_{12}$), so 18 is an element of $\\{A_n\\}$. The decimal number 14 is expressed as 1110 in binary. 1110 never appears in $\\{T_n\\}$, so 14 is not an element of $\\{A_n\\}$.
+
+The first several terms of $A_n$ are given as follows:
+
+$$\begin{array}{cr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & \ldots \\\\
+ A_n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 9 & 10 & 11 & 12 & 13 & 18 & \ldots \end{array}$$
+
+We can also verify that $A_{100} = 3251$ and $A_{1000} = 80\\,852\\,364\\,498$.
+
+Find the last 9 digits of $\displaystyle\sum_{k = 1}^{18} A_{{10}^k}$.
+
+# --hints--
+
+`subsequenceOfThueMorseSequence()` should return `178476944`.
+
+```js
+assert.strictEqual(subsequenceOfThueMorseSequence(), 178476944);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function subsequenceOfThueMorseSequence() {
+
+ return true;
+}
+
+subsequenceOfThueMorseSequence();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-362-squarefree-factors.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-362-squarefree-factors.md
new file mode 100644
index 00000000000..19f6b0f9cdc
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-362-squarefree-factors.md
@@ -0,0 +1,52 @@
+---
+id: 5900f4d61000cf542c50ffe9
+title: 'Problem 362: Squarefree factors'
+challengeType: 1
+forumTopicId: 302023
+dashedName: problem-362-squarefree-factors
+---
+
+# --description--
+
+Consider the number 54.
+
+54 can be factored in 7 distinct ways into one or more factors larger than 1:
+
+$$54, 2 × 27, 3 × 18, 6 × 9, 3 × 3 × 6, 2 × 3 × 9 \text{ and } 2 × 3 × 3 × 3$$
+
+If we require that the factors are all squarefree only two ways remain: $3 × 3 × 6$ and $2 × 3 × 3 × 3$.
+
+Let's call $Fsf(n)$ the number of ways $n$ can be factored into one or more squarefree factors larger than 1, so $Fsf(54) = 2$.
+
+Let $S(n)$ be $\sum Fsf(k)$ for $k = 2$ to $n$.
+
+$S(100) = 193$.
+
+Find $S(10\\,000\\,000\\,000)$.
+
+# --hints--
+
+`squarefreeFactors()` should return `457895958010`.
+
+```js
+assert.strictEqual(squarefreeFactors(), 457895958010);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function squarefreeFactors() {
+
+ return true;
+}
+
+squarefreeFactors();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-363-bzier-curves.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-363-bzier-curves.md
new file mode 100644
index 00000000000..df13df6a0c5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-363-bzier-curves.md
@@ -0,0 +1,56 @@
+---
+id: 5900f4d91000cf542c50ffeb
+title: 'Problem 363: Bézier Curves'
+challengeType: 1
+forumTopicId: 302024
+dashedName: problem-363-bzier-curves
+---
+
+# --description--
+
+A cubic Bézier curve is defined by four points: $P_0$, $P_1$, $P_2$ and $P_3$.
+
+The curve is constructed as follows:
+
+
+
+On the segments $P_0P_1$, $P_1P_2$ and $P_2P_3$ the points $Q_0$,$Q_1$ and $Q_2$ are drawn such that $\frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t$, with $t$ in [0,1].
+
+On the segments $Q_0Q_1$ and $Q_1Q_2$ the points $R_0$ and $R_1$ are drawn such that $\frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t$ for the same value of $t$.
+
+On the segment $R_0R_1$ the point $B$ is drawn such that $\frac{R_0B}{R_0R_1} = t$ for the same value of $t$.
+
+The Bézier curve defined by the points $P_0$, $P_1$, $P_2$, $P_3$ is the locus of $B$ as $Q_0$ takes all possible positions on the segment $P_0P_1$. (Please note that for all points the value of $t$ is the same.)
+
+From the construction it is clear that the Bézier curve will be tangent to the segments $P_0P_1$ in $P_0$ and $P_2P_3$ in $P_3$.
+
+A cubic Bézier curve with $P_0 = (1, 0)$, $P_1 = (1, v)$, $P_2 = (v, 1)$ and $P_3 = (0, 1)$ is used to approximate a quarter circle. The value $v > 0$ is chosen such that the area enclosed by the lines $OP_0$, $OP_3$ and the curve is equal to $\frac{π}{4}$ (the area of the quarter circle).
+
+By how many percent does the length of the curve differ from the length of the quarter circle? That is, if $L$ is the length of the curve, calculate $100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}}$. Give your answer rounded to 10 digits behind the decimal point.
+
+# --hints--
+
+`bezierCurves()` should return `0.0000372091`.
+
+```js
+assert.strictEqual(bezierCurves(), 0.0000372091);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function bezierCurves() {
+
+ return true;
+}
+
+bezierCurves();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-364-comfortable-distance.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-364-comfortable-distance.md
new file mode 100644
index 00000000000..83f8f7ec5d4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-364-comfortable-distance.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4d91000cf542c50ffea
+title: 'Problem 364: Comfortable distance'
+challengeType: 1
+forumTopicId: 302025
+dashedName: problem-364-comfortable-distance
+---
+
+# --description--
+
+There are $N$ seats in a row. $N$ people come after each other to fill the seats according to the following rules:
+
+1. If there is any seat whose adjacent seat(s) are not occupied take such a seat.
+2. If there is no such seat and there is any seat for which only one adjacent seat is occupied take such a seat.
+3. Otherwise take one of the remaining available seats.
+
+Let $T(N)$ be the number of possibilities that $N$ seats are occupied by $N$ people with the given rules. The following figure shows $T(4) = 8$.
+
+
+
+We can verify that $T(10) = 61\\,632$ and $T(1\\,000)\bmod 100\\,000\\,007 = 47\\,255\\,094$.
+
+Find $T(1\\,000\\,000)\bmod 100\\,000\\,007$.
+
+# --hints--
+
+`comfortableDistance()` should return `44855254`.
+
+```js
+assert.strictEqual(comfortableDistance(), 44855254);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function comfortableDistance() {
+
+ return true;
+}
+
+comfortableDistance();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-365-a-huge-binomial-coefficient.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-365-a-huge-binomial-coefficient.md
new file mode 100644
index 00000000000..46dc7abf5d6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-365-a-huge-binomial-coefficient.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4da1000cf542c50ffec
+title: 'Problem 365: A huge binomial coefficient'
+challengeType: 1
+forumTopicId: 302026
+dashedName: problem-365-a-huge-binomial-coefficient
+---
+
+# --description--
+
+The binomial coefficient $\displaystyle\binom{{10}^{18}}{{10}^9}$ is a number with more than 9 billion ($9 × {10}^9$) digits.
+
+Let $M(n, k, m)$ denote the binomial coefficient $\displaystyle\binom{n}{k}$ modulo $m$.
+
+Calculate $\sum M({10}^{18}, {10}^9, p \times q \times r)$ for $1000 < p < q < r < 5000$ and $p$, $q$, $r$ prime.
+
+# --hints--
+
+`hugeBinomialCoefficient()` should return `162619462356610300`.
+
+```js
+assert.strictEqual(hugeBinomialCoefficient(), 162619462356610300);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function hugeBinomialCoefficient() {
+
+ return true;
+}
+
+hugeBinomialCoefficient();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-366-stone-game-iii.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-366-stone-game-iii.md
new file mode 100644
index 00000000000..e4c51cb8c50
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-366-stone-game-iii.md
@@ -0,0 +1,68 @@
+---
+id: 5900f4da1000cf542c50ffed
+title: 'Problem 366: Stone Game III'
+challengeType: 1
+forumTopicId: 302027
+dashedName: problem-366-stone-game-iii
+---
+
+# --description--
+
+Two players, Anton and Bernhard, are playing the following game.
+
+There is one pile of $n$ stones.
+
+The first player may remove any positive number of stones, but not the whole pile.
+
+Thereafter, each player may remove at most twice the number of stones his opponent took on the previous move.
+
+The player who removes the last stone wins.
+
+E.g. $n = 5$
+
+If the first player takes anything more than one stone the next player will be able to take all remaining stones.
+
+If the first player takes one stone, leaving four, his opponent will take also one stone, leaving three stones.
+
+The first player cannot take all three because he may take at most $2 \times 1 = 2$ stones. So let's say he also takes one stone, leaving 2.
+
+The second player can take the two remaining stones and wins.
+
+So 5 is a losing position for the first player.
+
+For some winning positions there is more than one possible move for the first player.
+
+E.g. when $n = 17$ the first player can remove one or four stones.
+
+Let $M(n)$ be the maximum number of stones the first player can take from a winning position at his first turn and $M(n) = 0$ for any other position.
+
+$\sum M(n)$ for $n ≤ 100$ is 728.
+
+Find $\sum M(n)$ for $n ≤ {10}^{18}$. Give your answer modulo ${10}^8$.
+
+# --hints--
+
+`stoneGameThree()` should return `88351299`.
+
+```js
+assert.strictEqual(stoneGameThree(), 88351299);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function stoneGameThree() {
+
+ return true;
+}
+
+stoneGameThree();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-367-bozo-sort.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-367-bozo-sort.md
new file mode 100644
index 00000000000..01a24b3c665
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-367-bozo-sort.md
@@ -0,0 +1,56 @@
+---
+id: 5900f4db1000cf542c50ffee
+title: 'Problem 367: Bozo sort'
+challengeType: 1
+forumTopicId: 302028
+dashedName: problem-367-bozo-sort
+---
+
+# --description--
+
+Bozo sort, not to be confused with the slightly less efficient bogo sort, consists out of checking if the input sequence is sorted and if not swapping randomly two elements. This is repeated until eventually the sequence is sorted.
+
+If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of swaps, averaged over all $4!$ input sequences is $24.75$.
+
+The already sorted sequence takes 0 steps.
+
+In this problem we consider the following variant on bozo sort.
+
+If the sequence is not in order we pick three elements at random and shuffle these three elements randomly.
+
+All $3! = 6$ permutations of those three elements are equally likely.
+
+The already sorted sequence will take 0 steps.
+
+If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of shuffles, averaged over all $4!$ input sequences is $27.5$.
+
+Consider as input sequences the permutations of the first 11 natural numbers.
+
+Averaged over all $11!$ input sequences, what is the expected number of shuffles this sorting algorithm will perform? Give your answer rounded to the nearest integer.
+
+# --hints--
+
+`bozoSort()` should return `48271207`.
+
+```js
+assert.strictEqual(bozoSort(), 48271207);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function bozoSort() {
+
+ return true;
+}
+
+bozoSort();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-368-a-kempner-like-series.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-368-a-kempner-like-series.md
new file mode 100644
index 00000000000..afc2e6dc9b8
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-368-a-kempner-like-series.md
@@ -0,0 +1,51 @@
+---
+id: 5900f4dd1000cf542c50ffef
+title: 'Problem 368: A Kempner-like series'
+challengeType: 1
+forumTopicId: 302029
+dashedName: problem-368-a-kempner-like-series
+---
+
+# --description--
+
+The harmonic series $1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots$ is well known to be divergent.
+
+If we however omit from this series every term where the denominator has a 9 in it, the series remarkably enough converges to approximately 22.9206766193. This modified harmonic series is called the Kempner series.
+
+Let us now consider another modified harmonic series by omitting from the harmonic series every term where the denominator has 3 or more equal consecutive digits. One can verify that out of the first 1200 terms of the harmonic series, only 20 terms will be omitted.
+
+These 20 omitted terms are:
+
+$$\dfrac{1}{111}, \dfrac{1}{222}, \dfrac{1}{333}, \dfrac{1}{444}, \dfrac{1}{555}, \dfrac{1}{666}, \dfrac{1}{777}, \dfrac{1}{888}, \dfrac{1}{999}, \dfrac{1}{1000}, \dfrac{1}{1110}, \\\\
+\dfrac{1}{1111}, \dfrac{1}{1112}, \dfrac{1}{1113}, \dfrac{1}{1114}, \dfrac{1}{1115}, \dfrac{1}{1116}, \dfrac{1}{1117}, \dfrac{1}{1118}, \dfrac{1}{1119}$$
+
+This series converges as well.
+
+Find the value the series converges to. Give your answer rounded to 10 digits behind the decimal point.
+
+# --hints--
+
+`kempnerLikeSeries()` should return `253.6135092068`.
+
+```js
+assert.strictEqual(kempnerLikeSeries(), 253.6135092068);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function kempnerLikeSeries() {
+
+ return true;
+}
+
+kempnerLikeSeries();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-369-badugi.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-369-badugi.md
new file mode 100644
index 00000000000..b297bf965da
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-369-badugi.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4de1000cf542c50fff0
+title: 'Problem 369: Badugi'
+challengeType: 1
+forumTopicId: 302030
+dashedName: problem-369-badugi
+---
+
+# --description--
+
+In a standard 52 card deck of playing cards, a set of 4 cards is a Badugi if it contains 4 cards with no pairs and no two cards of the same suit.
+
+Let $f(n)$ be the number of ways to choose $n$ cards with a 4 card subset that is a Badugi. For example, there are $2\\,598\\,960$ ways to choose five cards from a standard 52 card deck, of which $514\\,800$ contain a 4 card subset that is a Badugi, so $f(5) = 514800$.
+
+Find $\sum f(n)$ for $4 ≤ n ≤ 13$.
+
+# --hints--
+
+`badugi()` should return `862400558448`.
+
+```js
+assert.strictEqual(badugi(), 862400558448);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function badugi() {
+
+ return true;
+}
+
+badugi();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-370-geometric-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-370-geometric-triangles.md
new file mode 100644
index 00000000000..dd37d167a05
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-370-geometric-triangles.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4de1000cf542c50fff1
+title: 'Problem 370: Geometric triangles'
+challengeType: 1
+forumTopicId: 302032
+dashedName: problem-370-geometric-triangles
+---
+
+# --description--
+
+Let us define a geometric triangle as an integer sided triangle with sides $a ≤ b ≤ c$ so that its sides form a geometric progression, i.e. $b^2 = a \times c$.
+
+An example of such a geometric triangle is the triangle with sides $a = 144$, $b = 156$ and $c = 169$.
+
+There are $861\\,805$ geometric triangles with $\text{perimeter} ≤ {10}^6$.
+
+How many geometric triangles exist with $\text{perimeter} ≤ 2.5 \times {10}^{13}$?
+
+# --hints--
+
+`geometricTriangles()` should return `41791929448408`.
+
+```js
+assert.strictEqual(geometricTriangles(), 41791929448408);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function geometricTriangles() {
+
+ return true;
+}
+
+geometricTriangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-371-licence-plates.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-371-licence-plates.md
new file mode 100644
index 00000000000..dee9928047e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-371-licence-plates.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4e01000cf542c50fff2
+title: 'Problem 371: Licence plates'
+challengeType: 1
+forumTopicId: 302033
+dashedName: problem-371-licence-plates
+---
+
+# --description--
+
+Oregon licence plates consist of three letters followed by a three digit number (each digit can be from [0...9]).
+
+While driving to work Seth plays the following game:
+
+Whenever the numbers of two licence plates seen on his trip add to 1000 that's a win.
+
+E.g. `MIC-012` and `HAN-988` is a win and `RYU-500` and `SET-500` too (as long as he sees them in the same trip).
+
+Find the expected number of plates he needs to see for a win. Give your answer rounded to 8 decimal places behind the decimal point.
+
+**Note:** We assume that each licence plate seen is equally likely to have any three digit number on it.
+
+# --hints--
+
+`licensePlates()` should return `40.66368097`.
+
+```js
+assert.strictEqual(licensePlates(), 40.66368097);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function licensePlates() {
+
+ return true;
+}
+
+licensePlates();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-372-pencils-of-rays.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-372-pencils-of-rays.md
new file mode 100644
index 00000000000..9a8e0ff315d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-372-pencils-of-rays.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4e11000cf542c50fff3
+title: 'Problem 372: Pencils of rays'
+challengeType: 1
+forumTopicId: 302034
+dashedName: problem-372-pencils-of-rays
+---
+
+# --description--
+
+Let $R(M, N)$ be the number of lattice points ($x$, $y$) which satisfy $M \lt x \le N$, $M \lt y \le N$ and $\left\lfloor\frac{y^2}{x^2}\right\rfloor$ is odd.
+
+We can verify that $R(0, 100) = 3\\,019$ and $R(100, 10\\,000) = 29\\,750\\,422$.
+
+Find $R(2 \times {10}^6, {10}^9)$.
+
+**Note:** $\lfloor x\rfloor$ represents the floor function.
+
+# --hints--
+
+`pencilsOfRays()` should return `301450082318807040`.
+
+```js
+assert.strictEqual(pencilsOfRays(), 301450082318807040);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pencilsOfRays() {
+
+ return true;
+}
+
+pencilsOfRays();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-373-circumscribed-circles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-373-circumscribed-circles.md
new file mode 100644
index 00000000000..dbe4e1d47e4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-373-circumscribed-circles.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4e11000cf542c50fff4
+title: 'Problem 373: Circumscribed Circles'
+challengeType: 1
+forumTopicId: 302035
+dashedName: problem-373-circumscribed-circles
+---
+
+# --description--
+
+Every triangle has a circumscribed circle that goes through the three vertices. Consider all integer sided triangles for which the radius of the circumscribed circle is integral as well.
+
+Let $S(n)$ be the sum of the radii of the circumscribed circles of all such triangles for which the radius does not exceed $n$.
+
+$S(100) = 4\\,950$ and $S(1\\,200) = 1\\,653\\,605$.
+
+Find $S({10}^7)$.
+
+# --hints--
+
+`circumscribedCircles()` should return `727227472448913`.
+
+```js
+assert.strictEqual(circumscribedCircles(), 727227472448913);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function circumscribedCircles() {
+
+ return true;
+}
+
+circumscribedCircles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-374-maximum-integer-partition-product.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-374-maximum-integer-partition-product.md
new file mode 100644
index 00000000000..e2578270e64
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-374-maximum-integer-partition-product.md
@@ -0,0 +1,54 @@
+---
+id: 5900f4e51000cf542c50fff6
+title: 'Problem 374: Maximum Integer Partition Product'
+challengeType: 1
+forumTopicId: 302036
+dashedName: problem-374-maximum-integer-partition-product
+---
+
+# --description--
+
+An integer partition of a number $n$ is a way of writing $n$ as a sum of positive integers.
+
+Partitions that differ only in the order of their summands are considered the same. A partition of $n$ into distinct parts is a partition of $n$ in which every part occurs at most once.
+
+The partitions of 5 into distinct parts are:
+
+5, 4 + 1 and 3 + 2.
+
+Let $f(n)$ be the maximum product of the parts of any such partition of $n$ into distinct parts and let $m(n)$ be the number of elements of any such partition of $n$ with that product.
+
+So $f(5) = 6$ and $m(5) = 2$.
+
+For $n = 10$ the partition with the largest product is $10 = 2 + 3 + 5$, which gives $f(10) = 30$ and $m(10) = 3$. And their product, $f(10) \times m(10) = 30 \times 3 = 90$
+
+It can be verified that $\sum f(n) \times m(n)$ for $1 ≤ n ≤ 100 = 1\\,683\\,550\\,844\\,462$.
+
+Find $\sum f(n) \times m(n)$ for $1 ≤ n ≤ {10}^{14}$. Give your answer modulo $982\\,451\\,653$, the 50 millionth prime.
+
+# --hints--
+
+`maximumIntegerPartitionProduct()` should return `334420941`.
+
+```js
+assert.strictEqual(maximumIntegerPartitionProduct(), 334420941);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function maximumIntegerPartitionProduct() {
+
+ return true;
+}
+
+maximumIntegerPartitionProduct();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-375-minimum-of-subsequences.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-375-minimum-of-subsequences.md
new file mode 100644
index 00000000000..082d94ef69c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-375-minimum-of-subsequences.md
@@ -0,0 +1,47 @@
+---
+id: 5900f4e41000cf542c50fff5
+title: 'Problem 375: Minimum of subsequences'
+challengeType: 1
+forumTopicId: 302037
+dashedName: problem-375-minimum-of-subsequences
+---
+
+# --description--
+
+Let $S_n$ be an integer sequence produced with the following pseudo-random number generator:
+
+$$\begin{align} S_0 & = 290\\,797 \\\\
+ S_{n + 1} & = {S_n}^2\bmod 50\\,515\\,093 \end{align}$$
+
+Let $A(i, j)$ be the minimum of the numbers $S_i, S_{i + 1}, \ldots, S_j$ for $i ≤ j$. Let $M(N) = \sum A(i, j)$ for $1 ≤ i ≤ j ≤ N$.
+
+We can verify that $M(10) = 432\\,256\\,955$ and $M(10\\,000) = 3\\,264\\,567\\,774\\,119$.
+
+Find $M(2\\,000\\,000\\,000)$.
+
+# --hints--
+
+`minimumOfSubsequences()` should return `7435327983715286000`.
+
+```js
+assert.strictEqual(minimumOfSubsequences(), 7435327983715286000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function minimumOfSubsequences() {
+
+ return true;
+}
+
+minimumOfSubsequences();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-376-nontransitive-sets-of-dice.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-376-nontransitive-sets-of-dice.md
new file mode 100644
index 00000000000..344a1e84e90
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-376-nontransitive-sets-of-dice.md
@@ -0,0 +1,69 @@
+---
+id: 5900f4e51000cf542c50fff7
+title: 'Problem 376: Nontransitive sets of dice'
+challengeType: 1
+forumTopicId: 302038
+dashedName: problem-376-nontransitive-sets-of-dice
+---
+
+# --description--
+
+Consider the following set of dice with nonstandard pips:
+
+$$\begin{array}{} \text{Die A: } & 1 & 4 & 4 & 4 & 4 & 4 \\\\
+ \text{Die B: } & 2 & 2 & 2 & 5 & 5 & 5 \\\\ \text{Die C: } & 3 & 3 & 3 & 3 & 3 & 6 \\\\
+\end{array}$$
+
+A game is played by two players picking a die in turn and rolling it. The player who rolls the highest value wins.
+
+If the first player picks die $A$ and the second player picks die $B$ we get
+
+$P(\text{second player wins}) = \frac{7}{12} > \frac{1}{2}$
+
+If the first player picks die $B$ and the second player picks die $C$ we get
+
+$P(\text{second player wins}) = \frac{7}{12} > \frac{1}{2}$
+
+If the first player picks die $C$ and the second player picks die $A$ we get
+
+$P(\text{second player wins}) = \frac{25}{36} > \frac{1}{2}$
+
+So whatever die the first player picks, the second player can pick another die and have a larger than 50% chance of winning. A set of dice having this property is called a nontransitive set of dice.
+
+We wish to investigate how many sets of nontransitive dice exist. We will assume the following conditions:
+
+- There are three six-sided dice with each side having between 1 and $N$ pips, inclusive.
+- Dice with the same set of pips are equal, regardless of which side on the die the pips are located.
+- The same pip value may appear on multiple dice; if both players roll the same value neither player wins.
+- The sets of dice $\\{A, B, C\\}$, $\\{B, C, A\\}$ and $\\{C, A, B\\}$ are the same set.
+
+For $N = 7$ we find there are 9780 such sets.
+
+How many are there for $N = 30$?
+
+# --hints--
+
+`nontransitiveSetsOfDice()` should return `973059630185670`.
+
+```js
+assert.strictEqual(nontransitiveSetsOfDice(), 973059630185670);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function nontransitiveSetsOfDice() {
+
+ return true;
+}
+
+nontransitiveSetsOfDice();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-377-sum-of-digits-experience-13.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-377-sum-of-digits-experience-13.md
new file mode 100644
index 00000000000..ff149a27b28
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-377-sum-of-digits-experience-13.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4e51000cf542c50fff8
+title: 'Problem 377: Sum of digits, experience 13'
+challengeType: 1
+forumTopicId: 302039
+dashedName: problem-377-sum-of-digits-experience-13
+---
+
+# --description--
+
+There are 16 positive integers that do not have a zero in their digits and that have a digital sum equal to 5, namely:
+
+5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 and 11111.
+
+Their sum is 17891.
+
+Let $f(n)$ be the sum of all positive integers that do not have a zero in their digits and have a digital sum equal to $n$.
+
+Find $\displaystyle\sum_{i=1}^{17} f(13^i)$. Give the last 9 digits as your answer.
+
+# --hints--
+
+`experience13()` should return `732385277`.
+
+```js
+assert.strictEqual(experience13(), 732385277);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function experience13() {
+
+ return true;
+}
+
+experience13();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-378-triangle-triples.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-378-triangle-triples.md
new file mode 100644
index 00000000000..e72ba4316c9
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-378-triangle-triples.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4e61000cf542c50fff9
+title: 'Problem 378: Triangle Triples'
+challengeType: 1
+forumTopicId: 302040
+dashedName: problem-378-triangle-triples
+---
+
+# --description--
+
+Let $T(n)$ be the $n^{\text{th}}$ triangle number, so $T(n) = \frac{n(n + 1)}{2}$.
+
+Let $dT(n)$ be the number of divisors of $T(n)$. E.g.: $T(7) = 28$ and $dT(7) = 6$.
+
+Let $Tr(n)$ be the number of triples ($i$, $j$, $k$) such that $1 ≤ i < j < k ≤ n$ and $dT(i) > dT(j) > dT(k)$. $Tr(20) = 14$, $Tr(100) = 5\\,772$ and $Tr(1000) = 11\\,174\\,776$.
+
+Find $Tr(60\\,000\\,000)$. Give the last 18 digits of your answer.
+
+# --hints--
+
+`triangleTriples()` should return `147534623725724700`.
+
+```js
+assert.strictEqual(triangleTriples(), 147534623725724700);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function triangleTriples() {
+
+ return true;
+}
+
+triangleTriples();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-379-least-common-multiple-count.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-379-least-common-multiple-count.md
new file mode 100644
index 00000000000..0f2fb896572
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-379-least-common-multiple-count.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4e81000cf542c50fffa
+title: 'Problem 379: Least common multiple count'
+challengeType: 1
+forumTopicId: 302041
+dashedName: problem-379-least-common-multiple-count
+---
+
+# --description--
+
+Let $f(n)$ be the number of couples ($x$, $y$) with $x$ and $y$ positive integers, $x ≤ y$ and the least common multiple of $x$ and $y$ equal to $n$.
+
+Let $g$ be the summatory function of $f$, i.e.: $g(n) = \sum f(i)$ for $1 ≤ i ≤ n$.
+
+You are given that $g({10}^6) = 37\\,429\\,395$.
+
+Find $g({10}^{12})$.
+
+# --hints--
+
+`leastCommonMultipleCount()` should return `132314136838185`.
+
+```js
+assert.strictEqual(leastCommonMultipleCount(), 132314136838185);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function leastCommonMultipleCount() {
+
+ return true;
+}
+
+leastCommonMultipleCount();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-380-amazing-mazes.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-380-amazing-mazes.md
new file mode 100644
index 00000000000..15ae5170a74
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-380-amazing-mazes.md
@@ -0,0 +1,54 @@
+---
+id: 5900f4e81000cf542c50fffb
+title: 'Problem 380: Amazing Mazes!'
+challengeType: 1
+forumTopicId: 302044
+dashedName: problem-380-amazing-mazes
+---
+
+# --description--
+
+An $m×n$ maze is an $m×n$ rectangular grid with walls placed between grid cells such that there is exactly one path from the top-left square to any other square. The following are examples of a 9×12 maze and a 15×20 maze:
+
+
+
+Let $C(m, n)$ be the number of distinct $m×n$ mazes. Mazes which can be formed by rotation and reflection from another maze are considered distinct.
+
+It can be verified that $C(1, 1) = 1$, $C(2, 2) = 4$, $C(3, 4) = 2415$, and $C(9, 12) = 2.5720\mathrm{e}\\,46$ (in scientific notation rounded to 5 significant digits).
+
+Find $C(100, 500)$ and write your answer as a string in scientific notation rounded to 5 significant digits.
+
+When giving your answer, use a lowercase e to separate mantissa and exponent. E.g. if the answer is 1234567891011 then the answer format would be the string `1.2346e12`.
+
+# --hints--
+
+`amazingMazes()` should return a string.
+
+```js
+assert(typeof amazingMazes() === 'string');
+```
+
+`amazingMazes()` should return the string `6.3202e25093`.
+
+```js
+assert.strictEqual(amazingMazes(), '6.3202e25093');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function amazingMazes() {
+
+ return true;
+}
+
+amazingMazes();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-381-prime-k-factorial.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-381-prime-k-factorial.md
new file mode 100644
index 00000000000..21d1936ca57
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-381-prime-k-factorial.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4ea1000cf542c50fffc
+title: 'Problem 381: (prime-k) factorial'
+challengeType: 1
+forumTopicId: 302045
+dashedName: problem-381-prime-k-factorial
+---
+
+# --description--
+
+For a prime $p$ let $S(p) = (\sum (p - k)!)\bmod (p)$ for $1 ≤ k ≤ 5$.
+
+For example, if $p = 7$,
+
+$$(7 - 1)! + (7 - 2)! + (7 - 3)! + (7 - 4)! + (7 - 5)! = 6! + 5! + 4! + 3! + 2! = 720 + 120 + 24 + 6 + 2 = 872$$
+
+As $872\bmod (7) = 4$, $S(7) = 4$.
+
+It can be verified that $\sum S(p) = 480$ for $5 ≤ p < 100$.
+
+Find $\sum S(p)$ for $5 ≤ p < {10}^8$.
+
+# --hints--
+
+`primeKFactorial()` should return `139602943319822`.
+
+```js
+assert.strictEqual(primeKFactorial(), 139602943319822);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeKFactorial() {
+
+ return true;
+}
+
+primeKFactorial();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-382-generating-polygons.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-382-generating-polygons.md
new file mode 100644
index 00000000000..605495d8fed
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-382-generating-polygons.md
@@ -0,0 +1,65 @@
+---
+id: 5900f4eb1000cf542c50fffd
+title: 'Problem 382: Generating polygons'
+challengeType: 1
+forumTopicId: 302046
+dashedName: problem-382-generating-polygons
+---
+
+# --description--
+
+A polygon is a flat shape consisting of straight line segments that are joined to form a closed chain or circuit. A polygon consists of at least three sides and does not self-intersect.
+
+A set $S$ of positive numbers is said to generate a polygon $P$ if:
+
+- no two sides of $P$ are the same length,
+- the length of every side of $P$ is in $S$, and
+- $S$ contains no other value.
+
+For example:
+
+The set {3, 4, 5} generates a polygon with sides 3, 4, and 5 (a triangle).
+
+The set {6, 9, 11, 24} generates a polygon with sides 6, 9, 11, and 24 (a quadrilateral).
+
+The sets {1, 2, 3} and {2, 3, 4, 9} do not generate any polygon at all.
+
+Consider the sequence $s$, defined as follows:
+
+- $s_1 = 1$, $s_2 = 2$, $s_3 = 3$
+- $s_n = s_{n - 1} + s_{n - 3}$ for $n > 3$.
+
+Let $U_n$ be the set $\\{s_1, s_2, \ldots, s_n\\}$. For example, $U_{10} = \\{1, 2, 3, 4, 6, 9, 13, 19, 28, 41\\}$.
+
+Let $f(n)$ be the number of subsets of $U_n$ which generate at least one polygon.
+
+For example, $f(5) = 7$, $f(10) = 501$ and $f(25) = 18\\,635\\,853$.
+
+Find the last 9 digits of $f({10}^{18})$.
+
+# --hints--
+
+`generatingPolygons()` should return `697003956`.
+
+```js
+assert.strictEqual(generatingPolygons(), 697003956);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function generatingPolygons() {
+
+ return true;
+}
+
+generatingPolygons();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-383-divisibility-comparison-between-factorials.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-383-divisibility-comparison-between-factorials.md
new file mode 100644
index 00000000000..4a851985199
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-383-divisibility-comparison-between-factorials.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4ed1000cf542c50ffff
+title: 'Problem 383: Divisibility comparison between factorials'
+challengeType: 1
+forumTopicId: 302047
+dashedName: problem-383-divisibility-comparison-between-factorials
+---
+
+# --description--
+
+Let $f_5(n)$ be the largest integer $x$ for which $5^x$ divides $n$.
+
+For example, $f_5(625\\,000) = 7$.
+
+Let $T_5(n)$ be the number of integers $i$ which satisfy $f_5((2 \times i - 1)!) < 2 \times f_5(i!)$ and $1 ≤ i ≤ n$.
+
+It can be verified that $T_5({10}^3) = 68$ and $T_5({10}^9) = 2\\,408\\,210$.
+
+Find $T_5({10}^{18})$.
+
+# --hints--
+
+`factorialDivisibilityComparison()` should return `22173624649806`.
+
+```js
+assert.strictEqual(factorialDivisibilityComparison(), 22173624649806);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function factorialDivisibilityComparison() {
+
+ return true;
+}
+
+factorialDivisibilityComparison();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-384-rudin-shapiro-sequence.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-384-rudin-shapiro-sequence.md
new file mode 100644
index 00000000000..9f11652c82f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-384-rudin-shapiro-sequence.md
@@ -0,0 +1,65 @@
+---
+id: 5900f4ed1000cf542c50fffe
+title: 'Problem 384: Rudin-Shapiro sequence'
+challengeType: 1
+forumTopicId: 302048
+dashedName: problem-384-rudin-shapiro-sequence
+---
+
+# --description--
+
+Define the sequence $a(n)$ as the number of adjacent pairs of ones in the binary expansion of $n$ (possibly overlapping).
+
+E.g.: $a(5) = a({101}_2) = 0$, $a(6) = a({110}_2) = 1$, $a(7) = a({111}_2) = 2$
+
+Define the sequence $b(n) = {(-1)}^{a(n)}$. This sequence is called the Rudin-Shapiro sequence.
+
+Also consider the summatory sequence of $b(n)$: $s(n) = \displaystyle\sum_{i = 0}^{n} b(i)$.
+
+The first couple of values of these sequences are:
+
+$$\begin{array}{lr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\\\
+ a(n) & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 2 \\\\ b(n) & 1 & 1 & 1 & -1 & 1 & 1 & -1 & 1 \\\\
+ s(n) & 1 & 2 & 3 & 2 & 3 & 4 & 3 & 4 \end{array}$$
+
+The sequence $s(n)$ has the remarkable property that all elements are positive and every positive integer $k$ occurs exactly $k$ times.
+
+Define $g(t, c)$, with $1 ≤ c ≤ t$, as the index in $s(n)$ for which $t$ occurs for the $c$'th time in $s(n)$.
+
+E.g.: $g(3, 3) = 6$, $g(4, 2) = 7$ and $g(54321, 12345) = 1\\,220\\,847\\,710$.
+
+Let $F(n)$ be the fibonacci sequence defined by:
+
+$$\begin{align} & F(0) = F(1) = 1 \text{ and} \\\\
+ & F(n) = F(n - 1) + F(n - 2) \text{ for } n > 1. \end{align}$$
+
+Define $GF(t) = g(F(t), F(t - 1))$.
+
+Find $\sum GF(t)$ for$ 2 ≤ t ≤ 45$.
+
+# --hints--
+
+`rudinShapiroSequence()` should return `3354706415856333000`.
+
+```js
+assert.strictEqual(rudinShapiroSequence(), 3354706415856333000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function rudinShapiroSequence() {
+
+ return true;
+}
+
+rudinShapiroSequence();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-385-ellipses-inside-triangles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-385-ellipses-inside-triangles.md
new file mode 100644
index 00000000000..13dcc0e7c5c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-385-ellipses-inside-triangles.md
@@ -0,0 +1,55 @@
+---
+id: 5900f4ee1000cf542c510000
+title: 'Problem 385: Ellipses inside triangles'
+challengeType: 1
+forumTopicId: 302049
+dashedName: problem-385-ellipses-inside-triangles
+---
+
+# --description--
+
+For any triangle $T$ in the plane, it can be shown that there is a unique ellipse with largest area that is completely inside $T$.
+
+
+
+For a given $n$, consider triangles $T$ such that:
+
+- the vertices of $T$ have integer coordinates with absolute value $≤ n$, and
+- the foci1 of the largest-area ellipse inside $T$ are $(\sqrt{13}, 0)$ and $(-\sqrt{13}, 0)$.
+
+Let $A(n)$ be the sum of the areas of all such triangles.
+
+For example, if $n = 8$, there are two such triangles. Their vertices are (-4,-3), (-4,3), (8,0) and (4,3), (4,-3), (-8,0), and the area of each triangle is 36. Thus $A(8) = 36 + 36 = 72$.
+
+It can be verified that $A(10) = 252$, $A(100) = 34\\,632$ and $A(1000) = 3\\,529\\,008$.
+
+Find $A(1\\,000\\,000\\,000)$.
+
+1The foci (plural of focus) of an ellipse are two points $A$ and $B$ such that for every point $P$ on the boundary of the ellipse, $AP + PB$ is constant.
+
+# --hints--
+
+`ellipsesInsideTriangles()` should return `3776957309612154000`.
+
+```js
+assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function ellipsesInsideTriangles() {
+
+ return true;
+}
+
+ellipsesInsideTriangles();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-386-maximum-length-of-an-antichain.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-386-maximum-length-of-an-antichain.md
new file mode 100644
index 00000000000..de0614e4651
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-386-maximum-length-of-an-antichain.md
@@ -0,0 +1,50 @@
+---
+id: 5900f4ef1000cf542c510001
+title: 'Problem 386: Maximum length of an antichain'
+challengeType: 1
+forumTopicId: 302050
+dashedName: problem-386-maximum-length-of-an-antichain
+---
+
+# --description--
+
+Let $n$ be an integer and $S(n)$ be the set of factors of $n$.
+
+A subset $A$ of $S(n)$ is called an antichain of $S(n)$ if $A$ contains only one element or if none of the elements of $A$ divides any of the other elements of $A$.
+
+For example: $S(30) = \\{1, 2, 3, 5, 6, 10, 15, 30\\}$
+
+$\\{2, 5, 6\\}$ is not an antichain of $S(30)$.
+
+$\\{2, 3, 5\\}$ is an antichain of $S(30)$.
+
+Let $N(n)$ be the maximum length of an antichain of $S(n)$.
+
+Find $\sum N(n)$ for $1 ≤ n ≤ {10}^8$
+
+# --hints--
+
+`maximumLengthOfAntichain()` should return `528755790`.
+
+```js
+assert.strictEqual(maximumLengthOfAntichain(), 528755790);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function maximumLengthOfAntichain() {
+
+ return true;
+}
+
+maximumLengthOfAntichain();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-387-harshad-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-387-harshad-numbers.md
new file mode 100644
index 00000000000..2b2ccbbaa0e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-387-harshad-numbers.md
@@ -0,0 +1,58 @@
+---
+id: 5900f4f11000cf542c510003
+title: 'Problem 387: Harshad Numbers'
+challengeType: 1
+forumTopicId: 302051
+dashedName: problem-387-harshad-numbers
+---
+
+# --description--
+
+A Harshad or Niven number is a number that is divisible by the sum of its digits.
+
+201 is a Harshad number because it is divisible by 3 (the sum of its digits.)
+
+When we truncate the last digit from 201, we get 20, which is a Harshad number.
+
+When we truncate the last digit from 20, we get 2, which is also a Harshad number.
+
+Let's call a Harshad number that, while recursively truncating the last digit, always results in a Harshad number a right truncatable Harshad number.
+
+Also:
+
+$\frac{201}{3} = 67$ which is prime.
+
+Let's call a Harshad number that, when divided by the sum of its digits, results in a prime a strong Harshad number.
+
+Now take the number 2011 which is prime. When we truncate the last digit from it we get 201, a strong Harshad number that is also right truncatable. Let's call such primes strong, right truncatable Harshad primes.
+
+You are given that the sum of the strong, right truncatable Harshad primes less than 10000 is 90619.
+
+Find the sum of the strong, right truncatable Harshad primes less than ${10}^{14}$.
+
+# --hints--
+
+`harshadNumbers()` should return `696067597313468`.
+
+```js
+assert.strictEqual(harshadNumbers(), 696067597313468);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function harshadNumbers() {
+
+ return true;
+}
+
+harshadNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-388-distinct-lines.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-388-distinct-lines.md
new file mode 100644
index 00000000000..4ff7f140070
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-388-distinct-lines.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4f11000cf542c510002
+title: 'Problem 388: Distinct Lines'
+challengeType: 1
+forumTopicId: 302052
+dashedName: problem-388-distinct-lines
+---
+
+# --description--
+
+Consider all lattice points ($a$, $b$, $c$) with $0 ≤ a, b, c ≤ N$.
+
+From the origin $O(0, 0, 0)$ all lines are drawn to the other lattice points. Let $D(N)$ be the number of distinct such lines.
+
+You are given that $D(1\\,000\\,000) = 831\\,909\\,254\\,469\\,114\\,121$.
+
+Find $D({10}^{10})$. Give as your answer the first nine digits followed by the last nine digits.
+
+# --hints--
+
+`distinctLines()` should return `831907372805130000`.
+
+```js
+assert.strictEqual(distinctLines(), 831907372805130000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function distinctLines() {
+
+ return true;
+}
+
+distinctLines();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-389-platonic-dice.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-389-platonic-dice.md
new file mode 100644
index 00000000000..081791ffe3b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-389-platonic-dice.md
@@ -0,0 +1,48 @@
+---
+id: 5900f4f21000cf542c510004
+title: 'Problem 389: Platonic Dice'
+challengeType: 1
+forumTopicId: 302053
+dashedName: problem-389-platonic-dice
+---
+
+# --description--
+
+An unbiased single 4-sided die is thrown and its value, $T$, is noted.
+
+$T$ unbiased 6-sided dice are thrown and their scores are added together. The sum, $C$, is noted.
+
+$C$ unbiased 8-sided dice are thrown and their scores are added together. The sum, $O$, is noted.
+
+$O$ unbiased 12-sided dice are thrown and their scores are added together. The sum, $D$, is noted.
+
+$D$ unbiased 20-sided dice are thrown and their scores are added together. The sum, $I$, is noted.
+
+Find the variance of $I$, and give your answer rounded to 4 decimal places.
+
+# --hints--
+
+`platonicDice()` should return `2406376.3623`.
+
+```js
+assert.strictEqual(platonicDice(), 2406376.3623);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function platonicDice() {
+
+ return true;
+}
+
+platonicDice();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-390-triangles-with-non-rational-sides-and-integral-area.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-390-triangles-with-non-rational-sides-and-integral-area.md
new file mode 100644
index 00000000000..fa9e6f08884
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-390-triangles-with-non-rational-sides-and-integral-area.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4f21000cf542c510005
+title: 'Problem 390: Triangles with non rational sides and integral area'
+challengeType: 1
+forumTopicId: 302055
+dashedName: problem-390-triangles-with-non-rational-sides-and-integral-area
+---
+
+# --description--
+
+Consider the triangle with sides $\sqrt{5}$, $\sqrt{65}$ and $\sqrt{68}$. It can be shown that this triangle has area 9.
+
+$S(n)$ is the sum of the areas of all triangles with sides $\sqrt{1 + b^2}$, $\sqrt{1 + c^2}$ and $\sqrt{b^2 + c^2}$ (for positive integers $b$ and $c$) that have an integral area not exceeding $n$.
+
+The example triangle has $b = 2$ and $c = 8$.
+
+$S({10}^6) = 18\\,018\\,206$.
+
+Find $S({10}^{10})$.
+
+# --hints--
+
+`nonRationalSidesAndIntegralArea()` should return `2919133642971`.
+
+```js
+assert.strictEqual(nonRationalSidesAndIntegralArea(), 2919133642971);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function nonRationalSidesAndIntegralArea() {
+
+ return true;
+}
+
+nonRationalSidesAndIntegralArea();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-391-hopping-game.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-391-hopping-game.md
new file mode 100644
index 00000000000..e94e14e527b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-391-hopping-game.md
@@ -0,0 +1,59 @@
+---
+id: 5900f4f31000cf542c510006
+title: 'Problem 391: Hopping Game'
+challengeType: 1
+forumTopicId: 302056
+dashedName: problem-391-hopping-game
+---
+
+# --description--
+
+Let $s_k$ be the number of 1’s when writing the numbers from 0 to $k$ in binary.
+
+For example, writing 0 to 5 in binary, we have 0, 1, 10, 11, 100, 101. There are seven 1’s, so $s_5 = 7$.
+
+The sequence $S = \\{s_k : k ≥ 0\\}$ starts $\\{0, 1, 2, 4, 5, 7, 9, 12, \ldots\\}$.
+
+A game is played by two players. Before the game starts, a number $n$ is chosen. A counter $c$ starts at 0. At each turn, the player chooses a number from 1 to $n$ (inclusive) and increases $c$ by that number. The resulting value of $c$ must be a member of $S$. If there are no more valid moves, the player loses.
+
+For example, with $n = 5$ and starting with $c = 0$:
+
+- Player 1 chooses 4, so $c$ becomes $0 + 4 = 4$.
+- Player 2 chooses 5, so $c$ becomes $4 + 5 = 9$.
+- Player 1 chooses 3, so $c$ becomes $9 + 3 = 12$.
+- etc.
+
+Note that $c$ must always belong to $S$, and each player can increase $c$ by at most $n$.
+
+Let $M(n)$ be the highest number the first player can choose at her first turn to force a win, and $M(n) = 0$ if there is no such move. For example, $M(2) = 2$, $M(7) = 1$ and $M(20) = 4$.
+
+It can be verified $\sum M{(n)}^3 = 8150$ for $1 ≤ n ≤ 20$.
+
+Find $\sum M{(n)}^3$ for $1 ≤ n ≤ 1000$.
+
+# --hints--
+
+`hoppingGame()` should return `61029882288`.
+
+```js
+assert.strictEqual(hoppingGame(), 61029882288);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function hoppingGame() {
+
+ return true;
+}
+
+hoppingGame();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-392-enmeshed-unit-circle.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-392-enmeshed-unit-circle.md
new file mode 100644
index 00000000000..7e40a574c29
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-392-enmeshed-unit-circle.md
@@ -0,0 +1,58 @@
+---
+id: 5900f4f41000cf542c510007
+title: 'Problem 392: Enmeshed unit circle'
+challengeType: 1
+forumTopicId: 302057
+dashedName: problem-392-enmeshed-unit-circle
+---
+
+# --description--
+
+A rectilinear grid is an orthogonal grid where the spacing between the gridlines does not have to be equidistant.
+
+An example of such grid is logarithmic graph paper.
+
+Consider rectilinear grids in the Cartesian coordinate system with the following properties:
+
+- The gridlines are parallel to the axes of the Cartesian coordinate system.
+- There are $N + 2$ vertical and $N + 2$ horizontal gridlines. Hence there are $(N + 1) \times (N + 1)$ rectangular cells.
+- The equations of the two outer vertical gridlines are $x = -1$ and $x = 1$.
+- The equations of the two outer horizontal gridlines are $y = -1$ and $y = 1$.
+- The grid cells are colored red if they overlap with the unit circle, black otherwise.
+
+For this problem we would like you to find the positions of the remaining $N$ inner horizontal and $N$ inner vertical gridlines so that the area occupied by the red cells is minimized.
+
+E.g. here is a picture of the solution for $N = 10$:
+
+
+
+The area occupied by the red cells for $N = 10$ rounded to 10 digits behind the decimal point is 3.3469640797.
+
+Find the positions for $N = 400$. Give as your answer the area occupied by the red cells rounded to 10 digits behind the decimal point.
+
+# --hints--
+
+`enmeshedUnitCircle()` should return `3.1486734435`.
+
+```js
+assert.strictEqual(enmeshedUnitCircle(), 3.1486734435);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function enmeshedUnitCircle() {
+
+ return true;
+}
+
+enmeshedUnitCircle();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-393-migrating-ants.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-393-migrating-ants.md
new file mode 100644
index 00000000000..28a0b4d745c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-393-migrating-ants.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4f61000cf542c510008
+title: 'Problem 393: Migrating ants'
+challengeType: 1
+forumTopicId: 302058
+dashedName: problem-393-migrating-ants
+---
+
+# --description--
+
+An $n × n$ grid of squares contains $n^2$ ants, one ant per square.
+
+All ants decide to move simultaneously to an adjacent square (usually 4 possibilities, except for ants on the edge of the grid or at the corners).
+
+We define $f(n)$ to be the number of ways this can happen without any ants ending on the same square and without any two ants crossing the same edge between two squares.
+
+You are given that $f(4) = 88$.
+
+Find $f(10)$.
+
+# --hints--
+
+`migratingAnts()` should return `112398351350823100`.
+
+```js
+assert.strictEqual(migratingAnts(), 112398351350823100);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function migratingAnts() {
+
+ return true;
+}
+
+migratingAnts();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-394-eating-pie.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-394-eating-pie.md
new file mode 100644
index 00000000000..a6b40bf39bc
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-394-eating-pie.md
@@ -0,0 +1,53 @@
+---
+id: 5900f4f71000cf542c510009
+title: 'Problem 394: Eating pie'
+challengeType: 1
+forumTopicId: 302059
+dashedName: problem-394-eating-pie
+---
+
+# --description--
+
+Jeff eats a pie in an unusual way.
+
+The pie is circular. He starts with slicing an initial cut in the pie along a radius.
+
+While there is at least a given fraction $F$ of pie left, he performs the following procedure:
+
+- He makes two slices from the pie centre to any point of what is remaining of the pie border, any point on the remaining pie border equally likely. This will divide the remaining pie into three pieces.
+- Going counterclockwise from the initial cut, he takes the first two pie pieces and eats them.
+
+When less than a fraction $F$ of pie remains, he does not repeat this procedure. Instead, he eats all of the remaining pie.
+
+
+
+For $x ≥ 1$, let $E(x)$ be the expected number of times Jeff repeats the procedure above with $F = \frac{1}{x}$. It can be verified that $E(1) = 1$, $E(2) ≈ 1.2676536759$, and $E(7.5) ≈ 2.1215732071$.
+
+Find $E(40)$ rounded to 10 decimal places behind the decimal point.
+
+# --hints--
+
+`eatingPie()` should return `3.2370342194`.
+
+```js
+assert.strictEqual(eatingPie(), 3.2370342194);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function eatingPie() {
+
+ return true;
+}
+
+eatingPie();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-395-pythagorean-tree.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-395-pythagorean-tree.md
new file mode 100644
index 00000000000..cff705c06fb
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-395-pythagorean-tree.md
@@ -0,0 +1,52 @@
+---
+id: 5900f4f71000cf542c51000a
+title: 'Problem 395: Pythagorean tree'
+challengeType: 1
+forumTopicId: 302060
+dashedName: problem-395-pythagorean-tree
+---
+
+# --description--
+
+The Pythagorean tree is a fractal generated by the following procedure:
+
+Start with a unit square. Then, calling one of the sides its base (in the animation, the bottom side is the base):
+
+1. Attach a right triangle to the side opposite the base, with the hypotenuse coinciding with that side and with the sides in a 3-4-5 ratio. Note that the smaller side of the triangle must be on the 'right' side with respect to the base (see animation).
+2. Attach a square to each leg of the right triangle, with one of its sides coinciding with that leg.
+3. Repeat this procedure for both squares, considering as their bases the sides touching the triangle.
+
+The resulting figure, after an infinite number of iterations, is the Pythagorean tree.
+
+
+
+It can be shown that there exists at least one rectangle, whose sides are parallel to the largest square of the Pythagorean tree, which encloses the Pythagorean tree completely.
+
+Find the smallest area possible for such a bounding rectangle, and give your answer rounded to 10 decimal places.
+
+# --hints--
+
+`pythagoreanTree()` should return `28.2453753155`.
+
+```js
+assert.strictEqual(pythagoreanTree(), 28.2453753155);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function pythagoreanTree() {
+
+ return true;
+}
+
+pythagoreanTree();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-396-weak-goodstein-sequence.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-396-weak-goodstein-sequence.md
new file mode 100644
index 00000000000..33d738c128b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-396-weak-goodstein-sequence.md
@@ -0,0 +1,62 @@
+---
+id: 5900f4f81000cf542c51000b
+title: 'Problem 396: Weak Goodstein sequence'
+challengeType: 1
+forumTopicId: 302061
+dashedName: problem-396-weak-goodstein-sequence
+---
+
+# --description--
+
+For any positive integer $n$, the $n$th weak Goodstein sequence $\\{g1, g2, g3, \ldots\\}$ is defined as:
+
+- $g_1 = n$
+- for $k > 1$, $g_k$ is obtained by writing $g_{k - 1}$ in base $k$, interpreting it as a base $k + 1$ number, and subtracting 1.
+
+The sequence terminates when $g_k$ becomes 0.
+
+For example, the $6$th weak Goodstein sequence is $\\{6, 11, 17, 25, \ldots\\}$:
+
+- $g_1 = 6$.
+- $g_2 = 11$ since $6 = 110_2$, $110_3 = 12$, and $12 - 1 = 11$.
+- $g_3 = 17$ since $11 = 102_3$, $102_4 = 18$, and $18 - 1 = 17$.
+- $g_4 = 25$ since $17 = 101_4$, $101_5 = 26$, and $26 - 1 = 25$.
+
+and so on.
+
+It can be shown that every weak Goodstein sequence terminates.
+
+Let $G(n)$ be the number of nonzero elements in the $n$th weak Goodstein sequence.
+
+It can be verified that $G(2) = 3$, $G(4) = 21$ and $G(6) = 381$.
+
+It can also be verified that $\sum G(n) = 2517$ for $1 ≤ n < 8$.
+
+Find the last 9 digits of $\sum G(n)$ for $1 ≤ n < 16$.
+
+# --hints--
+
+`weakGoodsteinSequence()` should return `173214653`.
+
+```js
+assert.strictEqual(weakGoodsteinSequence(), 173214653);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function weakGoodsteinSequence() {
+
+ return true;
+}
+
+weakGoodsteinSequence();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-397-triangle-on-parabola.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-397-triangle-on-parabola.md
new file mode 100644
index 00000000000..2d9fc181db3
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-397-triangle-on-parabola.md
@@ -0,0 +1,44 @@
+---
+id: 5900f4f91000cf542c51000c
+title: 'Problem 397: Triangle on parabola'
+challengeType: 1
+forumTopicId: 302062
+dashedName: problem-397-triangle-on-parabola
+---
+
+# --description--
+
+On the parabola $y = \frac{x^2}{k}$, three points $A(a, \frac{a^2}{k})$, $B(b, \frac{b^2}{k})$ and $C(c, \frac{c^2}{k})$ are chosen.
+
+Let $F(K, X)$ be the number of the integer quadruplets $(k, a, b, c)$ such that at least one angle of the triangle $ABC$ is 45°, with $1 ≤ k ≤ K$ and $-X ≤ a < b < c ≤ X$.
+
+For example, $F(1, 10) = 41$ and $F(10, 100) = 12\\,492$.
+
+Find $F({10}^6, {10}^9)$.
+
+# --hints--
+
+`triangleOnParabola()` should return `141630459461893730`.
+
+```js
+assert.strictEqual(triangleOnParabola(), 141630459461893730);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function triangleOnParabola() {
+
+ return true;
+}
+
+triangleOnParabola();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-398-cutting-rope.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-398-cutting-rope.md
new file mode 100644
index 00000000000..ade33707928
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-398-cutting-rope.md
@@ -0,0 +1,42 @@
+---
+id: 5900f4fa1000cf542c51000d
+title: 'Problem 398: Cutting rope'
+challengeType: 1
+forumTopicId: 302063
+dashedName: problem-398-cutting-rope
+---
+
+# --description--
+
+Inside a rope of length $n$, $n - 1$ points are placed with distance 1 from each other and from the endpoints. Among these points, we choose $m - 1$ points at random and cut the rope at these points to create $m$ segments.
+
+Let $E(n, m)$ be the expected length of the second-shortest segment. For example, $E(3, 2) = 2$ and $E(8, 3) = \frac{16}{7}$. Note that if multiple segments have the same shortest length the length of the second-shortest segment is defined as the same as the shortest length.
+
+Find $E({10}^7, 100)$. Give your answer rounded to 5 decimal places behind the decimal point.
+
+# --hints--
+
+`cuttingRope()` should return `2010.59096`.
+
+```js
+assert.strictEqual(cuttingRope(), 2010.59096);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function cuttingRope() {
+
+ return true;
+}
+
+cuttingRope();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-399-squarefree-fibonacci-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-399-squarefree-fibonacci-numbers.md
new file mode 100644
index 00000000000..37a34ad1549
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-399-squarefree-fibonacci-numbers.md
@@ -0,0 +1,60 @@
+---
+id: 5900f4fc1000cf542c51000e
+title: 'Problem 399: Squarefree Fibonacci Numbers'
+challengeType: 1
+forumTopicId: 302064
+dashedName: problem-399-squarefree-fibonacci-numbers
+---
+
+# --description--
+
+The first 15 fibonacci numbers are:
+
+$$1,1,2,3,5,8,13,21,34,55,89,144,233,377,610.$$
+
+It can be seen that 8 and 144 are not squarefree: 8 is divisible by 4 and 144 is divisible by 4 and by 9.
+
+So the first 13 squarefree fibonacci numbers are:
+
+$$1,1,2,3,5,13,21,34,55,89,233,377 \text{ and } 610.$$
+
+The $200$th squarefree fibonacci number is: 971183874599339129547649988289594072811608739584170445. The last sixteen digits of this number are: 1608739584170445 and in scientific notation this number can be written as `9.7e53`.
+
+Find the $100\\,000\\,000$th squarefree fibonacci number. Give as your answer as a string with its last sixteen digits followed by a comma followed by the number in scientific notation (rounded to one digit after the decimal point). For the $200$th squarefree number the answer would have been: `1608739584170445,9.7e53`
+
+**Note:** For this problem, assume that for every prime $p$, the first fibonacci number divisible by $p$ is not divisible by $p^2$ (this is part of Wall's conjecture). This has been verified for primes $≤ 3 \times {10}^{15}$, but has not been proven in general.
+
+If it happens that the conjecture is false, then the accepted answer to this problem isn't guaranteed to be the $100\\,000\\,000$th squarefree fibonacci number, rather it represents only a lower bound for that number.
+
+# --hints--
+
+`squarefreeFibonacciNumbers()` should return a string.
+
+```js
+assert(typeof squarefreeFibonacciNumbers() === 'string');
+```
+
+`squarefreeFibonacciNumbers()` should return the string `1508395636674243,6.5e27330467`.
+
+```js
+assert.strictEqual(squarefreeFibonacciNumbers(), '1508395636674243,6.5e27330467');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function squarefreeFibonacciNumbers() {
+
+ return true;
+}
+
+squarefreeFibonacciNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-400-fibonacci-tree-game.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-400-fibonacci-tree-game.md
new file mode 100644
index 00000000000..2b2e220949c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-301-to-400/problem-400-fibonacci-tree-game.md
@@ -0,0 +1,54 @@
+---
+id: 5900f4fe1000cf542c510010
+title: 'Problem 400: Fibonacci tree game'
+challengeType: 1
+forumTopicId: 302067
+dashedName: problem-400-fibonacci-tree-game
+---
+
+# --description--
+
+A Fibonacci tree is a binary tree recursively defined as:
+
+- $T(0)$ is the empty tree.
+- $T(1)$ is the binary tree with only one node.
+- $T(k)$ consists of a root node that has $T(k - 1)$ and $T(k - 2)$ as children.
+
+On such a tree two players play a take-away game. On each turn a player selects a node and removes that node along with the subtree rooted at that node. The player who is forced to take the root node of the entire tree loses.
+
+Here are the winning moves of the first player on the first turn for $T(k)$ from $k = 1$ to $k = 6$.
+
+
+
+Let $f(k)$ be the number of winning moves of the first player (i.e. the moves for which the second player has no winning strategy) on the first turn of the game when this game is played on $T(k)$.
+
+For example, $f(5) = 1$ and $f(10) = 17$.
+
+Find $f(10000)$. Give the last 18 digits of your answer.
+
+# --hints--
+
+`fibonacciTreeGame()` should return `438505383468410600`.
+
+```js
+assert.strictEqual(fibonacciTreeGame(), 438505383468410600);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function fibonacciTreeGame() {
+
+ return true;
+}
+
+fibonacciTreeGame();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-401-sum-of-squares-of-divisors.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-401-sum-of-squares-of-divisors.md
new file mode 100644
index 00000000000..eb0c0459100
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-401-sum-of-squares-of-divisors.md
@@ -0,0 +1,46 @@
+---
+id: 5900f4fd1000cf542c51000f
+title: 'Problem 401: Sum of squares of divisors'
+challengeType: 1
+forumTopicId: 302069
+dashedName: problem-401-sum-of-squares-of-divisors
+---
+
+# --description--
+
+The divisors of 6 are 1, 2, 3 and 6.
+
+The sum of the squares of these numbers is $1 + 4 + 9 + 36 = 50$.
+
+Let $\sigma_2(n)$ represent the sum of the squares of the divisors of $n$. Thus $\sigma_2(6) = 50$.
+
+Let $\Sigma_2$ represent the summatory function of $\sigma_2$, that is $\Sigma_2(n) = \sum \sigma_2(i)$ for $i=1$ to $n$. The first 6 values of $\Sigma_2$ are: 1, 6, 16, 37, 63 and 113.
+
+Find $\Sigma_2({10}^{15})$ modulo ${10}^9$.
+
+# --hints--
+
+`sumOfSquaresDivisors()` should return `281632621`.
+
+```js
+assert.strictEqual(sumOfSquaresDivisors(), 281632621);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumOfSquaresDivisors() {
+
+ return true;
+}
+
+sumOfSquaresDivisors();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-402-integer-valued-polynomials.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-402-integer-valued-polynomials.md
new file mode 100644
index 00000000000..cdda26ea631
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-402-integer-valued-polynomials.md
@@ -0,0 +1,51 @@
+---
+id: 5900f4ff1000cf542c510011
+title: 'Problem 402: Integer-valued polynomials'
+challengeType: 1
+forumTopicId: 302070
+dashedName: problem-402-integer-valued-polynomials
+---
+
+# --description--
+
+It can be shown that the polynomial $n^4 + 4n^3 + 2n^2 + 5n$ is a multiple of 6 for every integer $n$. It can also be shown that 6 is the largest integer satisfying this property.
+
+Define $M(a, b, c)$ as the maximum $m$ such that $n^4 + an^3 + bn^2 + cn$ is a multiple of $m$ for all integers $n$. For example, $M(4, 2, 5) = 6$.
+
+Also, define $S(N)$ as the sum of $M(a, b, c)$ for all $0 < a, b, c ≤ N$.
+
+We can verify that $S(10) = 1\\,972$ and $S(10\\,000) = 2\\,024\\,258\\,331\\,114$.
+
+Let $F_k$ be the Fibonacci sequence:
+
+- $F_0 = 0$, $F_1 = 1$ and
+- $F_k = F_{k - 1} + F_{k - 2}$ for $k ≥ 2$.
+
+Find the last 9 digits of $\sum S(F_k)$ for $2 ≤ k ≤ 1\\,234\\,567\\,890\\,123$.
+
+# --hints--
+
+`integerValuedPolynomials()` should return `356019862`.
+
+```js
+assert.strictEqual(integerValuedPolynomials(), 356019862);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function integerValuedPolynomials() {
+
+ return true;
+}
+
+integerValuedPolynomials();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-403-lattice-points-enclosed-by-parabola-and-line.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-403-lattice-points-enclosed-by-parabola-and-line.md
new file mode 100644
index 00000000000..e3f8bfaae35
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-403-lattice-points-enclosed-by-parabola-and-line.md
@@ -0,0 +1,46 @@
+---
+id: 5900f5001000cf542c510013
+title: 'Problem 403: Lattice points enclosed by parabola and line'
+challengeType: 1
+forumTopicId: 302071
+dashedName: problem-403-lattice-points-enclosed-by-parabola-and-line
+---
+
+# --description--
+
+For integers $a$ and $b$, we define $D(a, b)$ as the domain enclosed by the parabola $y = x^2$ and the line $y = ax + b: D(a, b) = \\{ (x, y) | x^2 ≤ y ≤ ax + b \\}$.
+
+$L(a, b)$ is defined as the number of lattice points contained in $D(a, b)$. For example, $L(1, 2) = 8$ and $L(2, -1) = 1$.
+
+We also define $S(N)$ as the sum of $L(a, b)$ for all the pairs ($a$, $b$) such that the area of $D(a, b)$ is a rational number and $|a|,|b| ≤ N$.
+
+We can verify that $S(5) = 344$ and $S(100) = 26\\,709\\,528$.
+
+Find $S({10}^{12})$. Give your answer $\bmod {10}^8$.
+
+# --hints--
+
+`latticePoints()` should return `18224771`.
+
+```js
+assert.strictEqual(latticePoints(), 18224771);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function latticePoints() {
+
+ return true;
+}
+
+latticePoints();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-404-crisscross-ellipses.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-404-crisscross-ellipses.md
new file mode 100644
index 00000000000..92690bd7a6d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-404-crisscross-ellipses.md
@@ -0,0 +1,54 @@
+---
+id: 5900f5001000cf542c510012
+title: 'Problem 404: Crisscross Ellipses'
+challengeType: 1
+forumTopicId: 302072
+dashedName: problem-404-crisscross-ellipses
+---
+
+# --description--
+
+$E_a$ is an ellipse with an equation of the form $x^2 + 4y^2 = 4a^2$.
+
+$E_a'$ is the rotated image of $E_a$ by $θ$ degrees counterclockwise around the origin $O(0, 0)$ for $0° < θ < 90°$.
+
+
+
+$b$ is the distance to the origin of the two intersection points closest to the origin and $c$ is the distance of the two other intersection points.
+
+We call an ordered triplet ($a$, $b$, $c$) a canonical ellipsoidal triplet if $a$, $b$ and $c$ are positive integers.
+
+For example, (209, 247, 286) is a canonical ellipsoidal triplet.
+
+Let $C(N)$ be the number of distinct canonical ellipsoidal triplets ($a$, $b$, $c$) for $a ≤ N$.
+
+It can be verified that $C({10}^3) = 7$, $C({10}^4) = 106$ and $C({10}^6) = 11\\,845$.
+
+Find $C({10}^{17})$.
+
+# --hints--
+
+`crisscrossEllipses()` should return `1199215615081353`.
+
+```js
+assert.strictEqual(crisscrossEllipses(), 1199215615081353);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function crisscrossEllipses() {
+
+ return true;
+}
+
+crisscrossEllipses();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-405-a-rectangular-tiling.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-405-a-rectangular-tiling.md
new file mode 100644
index 00000000000..43ceb097a66
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-405-a-rectangular-tiling.md
@@ -0,0 +1,52 @@
+---
+id: 5900f5021000cf542c510014
+title: 'Problem 405: A rectangular tiling'
+challengeType: 1
+forumTopicId: 302073
+dashedName: problem-405-a-rectangular-tiling
+---
+
+# --description--
+
+We wish to tile a rectangle whose length is twice its width.
+
+Let $T(0)$ be the tiling consisting of a single rectangle.
+
+For $n > 0$, let $T(n)$ be obtained from $T( n- 1)$ by replacing all tiles in the following manner:
+
+
+
+The following animation demonstrates the tilings $T(n)$ for $n$ from 0 to 5:
+
+
+
+Let $f(n)$ be the number of points where four tiles meet in $T(n)$. For example, $f(1) = 0$, $f(4) = 82$ and $f({10}^9)\bmod {17}^7 = 126\\,897\\,180$.
+
+Find $f({10}^k)$ for $k = {10}^{18}$, give your answer modulo ${17}^7$.
+
+# --hints--
+
+`rectangularTiling()` should return `237696125`.
+
+```js
+assert.strictEqual(rectangularTiling(), 237696125);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function rectangularTiling() {
+
+ return true;
+}
+
+rectangularTiling();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-406-guessing-game.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-406-guessing-game.md
new file mode 100644
index 00000000000..6907ad6dae2
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-406-guessing-game.md
@@ -0,0 +1,68 @@
+---
+id: 5900f5021000cf542c510015
+title: 'Problem 406: Guessing Game'
+challengeType: 1
+forumTopicId: 302074
+dashedName: problem-406-guessing-game
+---
+
+# --description--
+
+We are trying to find a hidden number selected from the set of integers {1, 2, ..., $n$} by asking questions. Each number (question) we ask, we get one of three possible answers:
+
+- "Your guess is lower than the hidden number" (and you incur a cost of a), or
+- "Your guess is higher than the hidden number" (and you incur a cost of b), or
+- "Yes, that's it!" (and the game ends).
+
+Given the value of $n$, $a$, and $b$, an optimal strategy minimizes the total cost for the worst possible case.
+
+For example, if $n = 5$, $a = 2$, and $b = 3$, then we may begin by asking "2" as our first question.
+
+If we are told that 2 is higher than the hidden number (for a cost of $b = 3$), then we are sure that "1" is the hidden number (for a total cost of 3).
+
+If we are told that 2 is lower than the hidden number (for a cost of $a = 2$), then our next question will be "4".
+
+If we are told that 4 is higher than the hidden number (for a cost of $b = 3$), then we are sure that "3" is the hidden number (for a total cost of $2 + 3 = \color{blue}{\mathbf{5}}$).
+
+If we are told that 4 is lower than the hidden number (for a cost of $a = 2$), then we are sure that "5" is the hidden number (for a total cost of $2 + 2 = \color{blue}{\mathbf{4}}$).
+
+Thus, the worst-case cost achieved by this strategy is 5. It can also be shown that this is the lowest worst-case cost that can be achieved. So, in fact, we have just described an optimal strategy for the given values of $n$, $a$, and $b$.
+
+Let $C(n, a, b)$ be the worst-case cost achieved by an optimal strategy for the given values of $n$, $a$, and $b$.
+
+Here are a few examples:
+
+$$\begin{align} & C(5, 2, 3) = 5 \\\\
+ & C(500, \sqrt{2}, \sqrt{3}) = 13.220\\,731\\,97\ldots \\\\ & C(20\\,000, 5, 7) = 82 \\\\
+ & C(2\\,000\\,000, √5, √7) = 49.637\\,559\\,55\ldots \\\\ \end{align}$$
+
+Let $F_k$ be the Fibonacci numbers: $F_k = F_{k - 1} + F_{k - 2}$ with base cases $F_1 = F_2 = 1$.
+
+Find $\displaystyle\sum_{k = 1}^{30} C({10}^{12}, \sqrt{k}, \sqrt{F_k})$, and give your answer rounded to 8 decimal places behind the decimal point.
+
+# --hints--
+
+`guessingGame()` should return `36813.12757207`.
+
+```js
+assert.strictEqual(guessingGame(), 36813.12757207);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function guessingGame() {
+
+ return true;
+}
+
+guessingGame();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-407-idempotents.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-407-idempotents.md
new file mode 100644
index 00000000000..f676b0c5b6e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-407-idempotents.md
@@ -0,0 +1,44 @@
+---
+id: 5900f5041000cf542c510016
+title: 'Problem 407: Idempotents'
+challengeType: 1
+forumTopicId: 302075
+dashedName: problem-407-idempotents
+---
+
+# --description--
+
+If we calculate $a^2\bmod 6$ for $0 ≤ a ≤ 5$ we get: 0, 1, 4, 3, 4, 1.
+
+The largest value of a such that $a^2 ≡ a\bmod 6$ is $4$.
+
+Let's call $M(n)$ the largest value of $a < n$ such that $a^2 ≡ a (\text{mod } n)$. So $M(6) = 4$.
+
+Find $\sum M(n)$ for $1 ≤ n ≤ {10}^7$.
+
+# --hints--
+
+`idempotents()` should return `39782849136421`.
+
+```js
+assert.strictEqual(idempotents(), 39782849136421);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function idempotents() {
+
+ return true;
+}
+
+idempotents();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-408-admissible-paths-through-a-grid.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-408-admissible-paths-through-a-grid.md
new file mode 100644
index 00000000000..260a1917a56
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-408-admissible-paths-through-a-grid.md
@@ -0,0 +1,46 @@
+---
+id: 5900f5091000cf542c51001b
+title: 'Problem 408: Admissible paths through a grid'
+challengeType: 1
+forumTopicId: 302076
+dashedName: problem-408-admissible-paths-through-a-grid
+---
+
+# --description--
+
+Let's call a lattice point ($x$, $y$) inadmissible if $x$, $y$ and $x + y$ are all positive perfect squares.
+
+For example, (9, 16) is inadmissible, while (0, 4), (3, 1) and (9, 4) are not.
+
+Consider a path from point ($x_1$, $y_1$) to point ($x_2$, $y_2$) using only unit steps north or east. Let's call such a path admissible if none of its intermediate points are inadmissible.
+
+Let $P(n)$ be the number of admissible paths from (0, 0) to ($n$, $n$). It can be verified that $P(5) = 252$, $P(16) = 596\\,994\\,440$ and $P(1\\,000)\bmod 1\\,000\\,000\\,007 = 341\\,920\\,854$.
+
+Find $P(10\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+
+# --hints--
+
+`admissiblePaths()` should return `299742733`.
+
+```js
+assert.strictEqual(admissiblePaths(), 299742733);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function admissiblePaths() {
+
+ return true;
+}
+
+admissiblePaths();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-409-nim-extreme.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-409-nim-extreme.md
new file mode 100644
index 00000000000..735a1c77781
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-409-nim-extreme.md
@@ -0,0 +1,48 @@
+---
+id: 5900f5061000cf542c510017
+title: 'Problem 409: Nim Extreme'
+challengeType: 1
+forumTopicId: 302077
+dashedName: problem-409-nim-extreme
+---
+
+# --description--
+
+Let $n$ be a positive integer. Consider nim positions where:
+
+- There are $n$ non-empty piles.
+- Each pile has size less than $2^n$.
+- No two piles have the same size.
+
+Let $W(n)$ be the number of winning nim positions satisfying the above conditions (a position is winning if the first player has a winning strategy).
+
+For example, $W(1) = 1$, $W(2) = 6$, $W(3) = 168$, $W(5) = 19\\,764\\,360$ and $W(100)\bmod 1\\,000\\,000\\,007 = 384\\,777\\,056$.
+
+Find $W(10\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+
+# --hints--
+
+`nimExtreme()` should return `253223948`.
+
+```js
+assert.strictEqual(nimExtreme(), 253223948);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function nimExtreme() {
+
+ return true;
+}
+
+nimExtreme();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-410-circle-and-tangent-line.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-410-circle-and-tangent-line.md
new file mode 100644
index 00000000000..fd9d28a1bab
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-410-circle-and-tangent-line.md
@@ -0,0 +1,46 @@
+---
+id: 5900f5071000cf542c510018
+title: 'Problem 410: Circle and tangent line'
+challengeType: 1
+forumTopicId: 302079
+dashedName: problem-410-circle-and-tangent-line
+---
+
+# --description--
+
+Let $C$ be the circle with radius $r$, $x^2 + y^2 = r^2$. We choose two points $P(a, b)$ and $Q(-a, c)$ so that the line passing through $P$ and $Q$ is tangent to $C$.
+
+For example, the quadruplet $(r, a, b, c) = (2, 6, 2, -7)$ satisfies this property.
+
+Let $F(R, X)$ be the number of the integer quadruplets $(r, a, b, c)$ with this property, and with $0 < r ≤ R$ and $0 < a ≤ X$.
+
+We can verify that $F(1, 5) = 10$, $F(2, 10) = 52$ and $F(10, 100) = 3384$.
+
+Find $F({10}^8, {10}^9) + F({10}^9, {10}^8)$.
+
+# --hints--
+
+`circleAndTangentLine()` should return `799999783589946600`.
+
+```js
+assert.strictEqual(circleAndTangentLine(), 799999783589946600);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function circleAndTangentLine() {
+
+ return true;
+}
+
+circleAndTangentLine();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-411-uphill-paths.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-411-uphill-paths.md
new file mode 100644
index 00000000000..09ace26cdea
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-411-uphill-paths.md
@@ -0,0 +1,50 @@
+---
+id: 5900f5081000cf542c510019
+title: 'Problem 411: Uphill paths'
+challengeType: 1
+forumTopicId: 302080
+dashedName: problem-411-uphill-paths
+---
+
+# --description--
+
+Let $n$ be a positive integer. Suppose there are stations at the coordinates $(x, y) = (2^i\bmod n, 3^i\bmod n)$ for $0 ≤ i ≤ 2n$. We will consider stations with the same coordinates as the same station.
+
+We wish to form a path from (0, 0) to ($n$, $n$) such that the $x$ and $y$ coordinates never decrease.
+
+Let $S(n)$ be the maximum number of stations such a path can pass through.
+
+For example, if $n = 22$, there are 11 distinct stations, and a valid path can pass through at most 5 stations. Therefore, $S(22) = 5$. The case is illustrated below, with an example of an optimal path:
+
+
+
+It can also be verified that $S(123) = 14$ and $S(10\\,000) = 48$.
+
+Find $\sum S(k^5)$ for $1 ≤ k ≤ 30$.
+
+# --hints--
+
+`uphillPaths()` should return `9936352`.
+
+```js
+assert.strictEqual(uphillPaths(), 9936352);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function uphillPaths() {
+
+ return true;
+}
+
+uphillPaths();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-412-gnomon-numbering.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-412-gnomon-numbering.md
new file mode 100644
index 00000000000..ac00f985c10
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-412-gnomon-numbering.md
@@ -0,0 +1,52 @@
+---
+id: 5900f5081000cf542c51001a
+title: 'Problem 412: Gnomon numbering'
+challengeType: 1
+forumTopicId: 302081
+dashedName: problem-412-gnomon-numbering
+---
+
+# --description--
+
+For integers $m$, $n$ ($0 ≤ n < m$), let $L(m, n)$ be an $m×m$ grid with the top-right $n×n$ grid removed.
+
+For example, $L(5, 3)$ looks like this:
+
+
+
+We want to number each cell of $L(m, n)$ with consecutive integers 1, 2, 3, ... such that the number in every cell is smaller than the number below it and to the left of it.
+
+For example, here are two valid numberings of $L(5, 3)$:
+
+
+
+Let $LC(m, n)$ be the number of valid numberings of $L(m, n)$. It can be verified that $LC(3, 0) = 42$, $LC(5, 3) = 250\\,250$, $LC(6, 3) = 406\\,029\\,023\\,400$ and $LC(10, 5)\bmod 76\\,543\\,217 = 61\\,251\\,715$.
+
+Find $LC(10\\,000, 5\\,000)\bmod 76\\,543\\,217$.
+
+# --hints--
+
+`gnomonNumbering()` should return `38788800`.
+
+```js
+assert.strictEqual(gnomonNumbering(), 38788800);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function gnomonNumbering() {
+
+ return true;
+}
+
+gnomonNumbering();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-413-one-child-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-413-one-child-numbers.md
new file mode 100644
index 00000000000..0a50da9e14d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-413-one-child-numbers.md
@@ -0,0 +1,46 @@
+---
+id: 5900f50a1000cf542c51001c
+title: 'Problem 413: One-child Numbers'
+challengeType: 1
+forumTopicId: 302082
+dashedName: problem-413-one-child-numbers
+---
+
+# --description--
+
+We say that a $d$-digit positive number (no leading zeros) is a one-child number if exactly one of its sub-strings is divisible by $d$.
+
+For example, 5671 is a 4-digit one-child number. Among all its sub-strings 5, 6, 7, 1, 56, 67, 71, 567, 671 and 5671, only 56 is divisible by 4.
+
+Similarly, 104 is a 3-digit one-child number because only 0 is divisible by 3. 1132451 is a 7-digit one-child number because only 245 is divisible by 7.
+
+Let $F(N)$ be the number of the one-child numbers less than $N$. We can verify that $F(10) = 9$, $F({10}^3) = 389$ and $F({10}^7) = 277\\,674$.
+
+Find $F({10}^{19})$.
+
+# --hints--
+
+`oneChildNumbers()` should return `3079418648040719`.
+
+```js
+assert.strictEqual(oneChildNumbers(), 3079418648040719);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function oneChildNumbers() {
+
+ return true;
+}
+
+oneChildNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-414-kaprekar-constant.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-414-kaprekar-constant.md
new file mode 100644
index 00000000000..e50ab2c9a7e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-414-kaprekar-constant.md
@@ -0,0 +1,64 @@
+---
+id: 5900f50b1000cf542c51001d
+title: 'Problem 414: Kaprekar constant'
+challengeType: 1
+forumTopicId: 302083
+dashedName: problem-414-kaprekar-constant
+---
+
+# --description--
+
+6174 is a remarkable number; if we sort its digits in increasing order and subtract that number from the number you get when you sort the digits in decreasing order, we get $7641 - 1467 = 6174$.
+
+Even more remarkable is that if we start from any 4 digit number and repeat this process of sorting and subtracting, we'll eventually end up with 6174 or immediately with 0 if all digits are equal.
+
+This also works with numbers that have less than 4 digits if we pad the number with leading zeroes until we have 4 digits.
+
+E.g. let's start with the number 0837:
+
+$$\begin{align} & 8730 - 0378 = 8352 \\\\
+ & 8532 - 2358 = 6174 \end{align}$$
+
+6174 is called the Kaprekar constant. The process of sorting and subtracting and repeating this until either 0 or the Kaprekar constant is reached is called the Kaprekar routine.
+
+We can consider the Kaprekar routine for other bases and number of digits. Unfortunately, it is not guaranteed a Kaprekar constant exists in all cases; either the routine can end up in a cycle for some input numbers or the constant the routine arrives at can be different for different input numbers. However, it can be shown that for 5 digits and a base $b = 6t + 3 ≠ 9$, a Kaprekar constant exists.
+
+E.g. base 15: ${(10, 4, 14, 9, 5)}\_{15}$ base 21: $(14, 6, 20, 13, 7)\_{21}$
+
+Define $C_b$ to be the Kaprekar constant in base $b$ for 5 digits. Define the function $sb(i)$ to be:
+
+- 0 if $i = C_b$ or if $i$ written in base $b$ consists of 5 identical digits
+- the number of iterations it takes the Kaprekar routine in base $b$ to arrive at $C_b$, otherwise
+
+Note that we can define $sb(i)$ for all integers $i < b^5$. If $i$ written in base $b$ takes less than 5 digits, the number is padded with leading zero digits until we have 5 digits before applying the Kaprekar routine.
+
+Define $S(b)$ as the sum of $sb(i)$ for $0 < i < b^5$. E.g. $S(15) = 5\\,274\\,369$ $S(111) = 400\\,668\\,930\\,299$
+
+Find the sum of $S(6k + 3)$ for $2 ≤ k ≤ 300$. Give the last 18 digits as your answer.
+
+# --hints--
+
+`kaprekarConstant()` should return `552506775824935500`.
+
+```js
+assert.strictEqual(kaprekarConstant(), 552506775824935500);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function kaprekarConstant() {
+
+ return true;
+}
+
+kaprekarConstant();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-415-titanic-sets.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-415-titanic-sets.md
new file mode 100644
index 00000000000..a03c026f9ae
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-415-titanic-sets.md
@@ -0,0 +1,46 @@
+---
+id: 5900f50c1000cf542c51001e
+title: 'Problem 415: Titanic sets'
+challengeType: 1
+forumTopicId: 302084
+dashedName: problem-415-titanic-sets
+---
+
+# --description--
+
+A set of lattice points $S$ is called a titanic set if there exists a line passing through exactly two points in $S$.
+
+An example of a titanic set is $S = \\{(0, 0), (0, 1), (0, 2), (1, 1), (2, 0), (1, 0)\\}$, where the line passing through (0, 1) and (2, 0) does not pass through any other point in $S$.
+
+On the other hand, the set {(0, 0), (1, 1), (2, 2), (4, 4)} is not a titanic set since the line passing through any two points in the set also passes through the other two.
+
+For any positive integer $N$, let $T(N)$ be the number of titanic sets $S$ whose every point ($x$, $y$) satisfies $0 ≤ x$, $y ≤ N$. It can be verified that $T(1) = 11$, $T(2) = 494$, $T(4) = 33\\,554\\,178$, $T(111)\bmod {10}^8 = 13\\,500\\,401$ and $T({10}^5)\bmod {10}^8 = 63\\,259\\,062$.
+
+Find $T({10}^{11})\bmod {10}^8$.
+
+# --hints--
+
+`titanicSets()` should return `55859742`.
+
+```js
+assert.strictEqual(titanicSets(), 55859742);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function titanicSets() {
+
+ return true;
+}
+
+titanicSets();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-416-a-frogs-trip.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-416-a-frogs-trip.md
new file mode 100644
index 00000000000..048adb254cd
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-416-a-frogs-trip.md
@@ -0,0 +1,44 @@
+---
+id: 5900f50e1000cf542c510020
+title: 'Problem 416: A frog''s trip'
+challengeType: 1
+forumTopicId: 302085
+dashedName: problem-416-a-frogs-trip
+---
+
+# --description--
+
+A row of $n$ squares contains a frog in the leftmost square. By successive jumps the frog goes to the rightmost square and then back to the leftmost square. On the outward trip he jumps one, two or three squares to the right, and on the homeward trip he jumps to the left in a similar manner. He cannot jump outside the squares. He repeats the round-trip travel $m$ times.
+
+Let $F(m, n)$ be the number of the ways the frog can travel so that at most one square remains unvisited.
+
+For example, $F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$ and $F(2, 100)\bmod {10}^9 = 429\\,619\\,151$.
+
+Find the last 9 digits of $F(10, {10}^{12})$.
+
+# --hints--
+
+`frogsTrip()` should return `898082747`.
+
+```js
+assert.strictEqual(frogsTrip(), 898082747);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function frogsTrip() {
+
+ return true;
+}
+
+frogsTrip();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-417-reciprocal-cycles-ii.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-417-reciprocal-cycles-ii.md
new file mode 100644
index 00000000000..aa0880c13f4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-417-reciprocal-cycles-ii.md
@@ -0,0 +1,53 @@
+---
+id: 5900f50d1000cf542c51001f
+title: 'Problem 417: Reciprocal cycles II'
+challengeType: 1
+forumTopicId: 302086
+dashedName: problem-417-reciprocal-cycles-ii
+---
+
+# --description--
+
+A unit fraction contains 1 in the numerator. The decimal representation of the unit fractions with denominators 2 to 10 are given:
+
+$$\begin{align} & \frac{1}{2} = 0.5 \\\\
+ & \frac{1}{3} = 0.(3) \\\\ & \frac{1}{4} = 0.25 \\\\
+ & \frac{1}{5} = 0.2 \\\\ & \frac{1}{6} = 0.1(6) \\\\
+ & \frac{1}{7} = 0.(142857) \\\\ & \frac{1}{8} = 0.125 \\\\
+ & \frac{1}{9} = 0.(1) \\\\ & \frac{1}{10} = 0.1 \\\\
+\end{align}$$
+
+Where $0.1(6)$ means $0.166666\ldots$, and has a 1-digit recurring cycle. It can be seen that $\frac{1}{7}$ has a 6-digit recurring cycle.
+
+Unit fractions whose denominator has no other prime factors than 2 and/or 5 are not considered to have a recurring cycle. We define the length of the recurring cycle of those unit fractions as 0.
+
+Let $L(n)$ denote the length of the recurring cycle of $\frac{1}{n}$. You are given that $\sum L(n)$ for $3 ≤ n ≤ 1\\,000\\,000$ equals $55\\,535\\,191\\,115$.
+
+Find $\sum L(n)$ for $3 ≤ n ≤ 100\\,000\\,000$.
+
+# --hints--
+
+`reciprocalCyclesTwo()` should return `446572970925740`.
+
+```js
+assert.strictEqual(reciprocalCyclesTwo(), 446572970925740);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function reciprocalCyclesTwo() {
+
+ return true;
+}
+
+reciprocalCyclesTwo();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-418-factorisation-triples.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-418-factorisation-triples.md
new file mode 100644
index 00000000000..0c376474a32
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-418-factorisation-triples.md
@@ -0,0 +1,47 @@
+---
+id: 5900f50f1000cf542c510021
+title: 'Problem 418: Factorisation triples'
+challengeType: 1
+forumTopicId: 302087
+dashedName: problem-418-factorisation-triples
+---
+
+# --description--
+
+Let $n$ be a positive integer. An integer triple ($a$, $b$, $c$) is called a factorisation triple of $n$ if:
+
+- $1 ≤ a ≤ b ≤ c$
+- $a \times b \times c = n$.
+
+Define $f(n)$ to be $a + b + c$ for the factorisation triple ($a$, $b$, $c$) of $n$ which minimises $\frac{c}{a}$. One can show that this triple is unique.
+
+For example, $f(165) = 19$, $f(100\\,100) = 142$ and $f(20!) = 4\\,034\\,872$.
+
+Find $f(43!)$.
+
+# --hints--
+
+`factorisationTriples()` should return `1177163565297340400`.
+
+```js
+assert.strictEqual(factorisationTriples(), 1177163565297340400);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function factorisationTriples() {
+
+ return true;
+}
+
+factorisationTriples();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-419-look-and-say-sequence.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-419-look-and-say-sequence.md
new file mode 100644
index 00000000000..4143ab36ccb
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-419-look-and-say-sequence.md
@@ -0,0 +1,65 @@
+---
+id: 5900f5101000cf542c510022
+title: 'Problem 419: Look and say sequence'
+challengeType: 1
+forumTopicId: 302088
+dashedName: problem-419-look-and-say-sequence
+---
+
+# --description--
+
+The look and say sequence goes 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ...
+
+The sequence starts with 1 and all other members are obtained by describing the previous member in terms of consecutive digits.
+
+It helps to do this out loud:
+
+1 is 'one one' $→ 11$
+
+11 is 'two ones' $→ 21$
+
+21 is 'one two and one one' $→ 1211$
+
+1211 is 'one one, one two and two ones' $→ 111221$
+
+111221 is 'three ones, two twos and one one' $→ 312211$
+
+...
+
+Define $A(n)$, $B(n)$ and $C(n)$ as the number of ones, twos and threes in the $n$'th element of the sequence respectively. One can verify that $A(40) = 31\\,254$, $B(40) = 20\\,259$ and $C(40) = 11\\,625$.
+
+Find $A(n)$, $B(n)$ and $C(n)$ for $n = {10}^{12}$. Give your answer modulo $2^{30}$ as a string and separate your values for $A$, $B$ and $C$ by a comma. E.g. for $n = 40$ the answer would be `31254,20259,11625`.
+
+# --hints--
+
+`lookAndSaySequence()` should return a string.
+
+```js
+assert(typeof lookAndSaySequence() === 'string');
+```
+
+
+`lookAndSaySequence()` should return the string `998567458,1046245404,43363922`.
+
+```js
+assert.strictEqual(lookAndSaySequence(), '998567458,1046245404,43363922');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function lookAndSaySequence() {
+
+ return true;
+}
+
+lookAndSaySequence();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-420-2x2-positive-integer-matrix.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-420-2x2-positive-integer-matrix.md
new file mode 100644
index 00000000000..50a7c676cb8
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-420-2x2-positive-integer-matrix.md
@@ -0,0 +1,55 @@
+---
+id: 5900f5111000cf542c510023
+title: 'Problem 420: 2x2 positive integer matrix'
+challengeType: 1
+forumTopicId: 302090
+dashedName: problem-420-2x2-positive-integer-matrix
+---
+
+# --description--
+
+A positive integer matrix is a matrix whose elements are all positive integers.
+
+Some positive integer matrices can be expressed as a square of a positive integer matrix in two different ways. Here is an example:
+
+$$\begin{pmatrix} 40 & 12 \\\\
+ 48 & 40 \end{pmatrix} =
+{\begin{pmatrix}
+ 2 & 3 \\\\
+ 12 & 2 \end{pmatrix}}^2 =
+{\begin{pmatrix}
+ 6 & 1 \\\\
+ 4 & 6 \end{pmatrix}}^2$$
+
+We define $F(N)$ as the number of the 2x2 positive integer matrices which have a trace less than N and which can be expressed as a square of a positive integer matrix in two different ways.
+
+We can verify that $F(50) = 7$ and $F(1000) = 1019$.
+
+Find $F({10}^7)$.
+
+# --hints--
+
+`positiveIntegerMatrix()` should return `145159332`.
+
+```js
+assert.strictEqual(positiveIntegerMatrix(), 145159332);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function positiveIntegerMatrix() {
+
+ return true;
+}
+
+positiveIntegerMatrix();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-421-prime-factors-of-n151.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-421-prime-factors-of-n151.md
new file mode 100644
index 00000000000..f94cb95bc48
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-421-prime-factors-of-n151.md
@@ -0,0 +1,50 @@
+---
+id: 5900f5131000cf542c510024
+title: 'Problem 421: Prime factors of n^15+1'
+challengeType: 1
+forumTopicId: 302091
+dashedName: problem-421-prime-factors-of-n151
+---
+
+# --description--
+
+Numbers of the form $n^{15} + 1$ are composite for every integer $n > 1$.
+
+For positive integers $n$ and $m$ let $s(n, m)$ be defined as the sum of the distinct prime factors of $n^{15} + 1$ not exceeding $m$.
+
+E.g. $2^{15} + 1 = 3 × 3 × 11 × 331$.
+
+So $s(2, 10) = 3$ and $s(2, 1000) = 3 + 11 + 331 = 345$.
+
+Also ${10}^{15} + 1 = 7 × 11 × 13 × 211 × 241 × 2161 × 9091$.
+
+So $s(10, 100) = 31$ and $s(10, 1000) = 483$.
+
+Find $\sum s(n, {10}^8)$ for $1 ≤ n ≤ {10}^{11}$.
+
+# --hints--
+
+`primeFactorsOfN15Plus1()` should return `2304215802083466200`.
+
+```js
+assert.strictEqual(primeFactorsOfN15Plus1(), 2304215802083466200);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeFactorsOfN15Plus1() {
+
+ return true;
+}
+
+primeFactorsOfN15Plus1();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-422-sequence-of-points-on-a-hyperbola.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-422-sequence-of-points-on-a-hyperbola.md
new file mode 100644
index 00000000000..7ea875b71ab
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-422-sequence-of-points-on-a-hyperbola.md
@@ -0,0 +1,54 @@
+---
+id: 5900f5131000cf542c510025
+title: 'Problem 422: Sequence of points on a hyperbola'
+challengeType: 1
+forumTopicId: 302092
+dashedName: problem-422-sequence-of-points-on-a-hyperbola
+---
+
+# --description--
+
+Let $H$ be the hyperbola defined by the equation $12x^2 + 7xy - 12y^2 = 625$.
+
+Next, define $X$ as the point (7, 1). It can be seen that $X$ is in $H$.
+
+Now we define a sequence of points in $H, \\{P_i : i ≥ 1\\}$, as:
+
+- $P_1 = (13, \frac{61}{4})$.
+- $P_2 = (\frac{-43}{6}, -4)$.
+- For $i > 2$, $P_i$ is the unique point in $H$ that is different from $P_{i - 1}$ and such that line $P_iP_{i - 1}$ is parallel to line $P_{i - 2}X$. It can be shown that $P_i$ is well-defined, and that its coordinates are always rational.
+
+
+
+You are given that $P_3 = (\frac{-19}{2}, \frac{-229}{24})$, $P_4 = (\frac{1267}{144}, \frac{-37}{12})$ and $P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784})$.
+
+Find $P_n$ for $n = {11}^{14}$ in the following format: If $P_n = (\frac{a}{b}, \frac{c}{d})$ where the fractions are in lowest terms and the denominators are positive, then the answer is $(a + b + c + d)\bmod 1\\,000\\,000\\,007$.
+
+For $n = 7$, the answer would have been: $806\\,236\\,837$.
+
+# --hints--
+
+`sequenceOfPointsOnHyperbola()` should return `92060460`.
+
+```js
+assert.strictEqual(sequenceOfPointsOnHyperbola(), 92060460);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sequenceOfPointsOnHyperbola() {
+
+ return true;
+}
+
+sequenceOfPointsOnHyperbola();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-423-consecutive-die-throws.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-423-consecutive-die-throws.md
new file mode 100644
index 00000000000..9969311f0de
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-423-consecutive-die-throws.md
@@ -0,0 +1,59 @@
+---
+id: 5900f5141000cf542c510027
+title: 'Problem 423: Consecutive die throws'
+challengeType: 1
+forumTopicId: 302093
+dashedName: problem-423-consecutive-die-throws
+---
+
+# --description--
+
+Let $n$ be a positive integer.
+
+A 6-sided die is thrown $n$ times. Let $c$ be the number of pairs of consecutive throws that give the same value.
+
+For example, if $n = 7$ and the values of the die throws are (1, 1, 5, 6, 6, 6, 3), then the following pairs of consecutive throws give the same value:
+
+$$\begin{align} & (\underline{1}, \underline{1}, 5, 6, 6, 6, 3) \\\\
+ & (1, 1, 5, \underline{6}, \underline{6}, 6, 3) \\\\ & (1, 1, 5, 6, \underline{6}, \underline{6}, 3) \end{align}$$
+
+Therefore, $c = 3$ for (1, 1, 5, 6, 6, 6, 3).
+
+Define $C(n)$ as the number of outcomes of throwing a 6-sided die $n$ times such that $c$ does not exceed $π(n)$.1
+
+For example, $C(3) = 216$, $C(4) = 1290$, $C(11) = 361\\,912\\,500$ and $C(24) = 4\\,727\\,547\\,363\\,281\\,250\\,000$.
+
+Define $S(L)$ as $\sum C(n)$ for $1 ≤ n ≤ L$.
+
+For example, $S(50)\bmod 1\\,000\\,000\\,007 = 832\\,833\\,871$.
+
+Find $S(50\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+
+1 $π$ denotes the prime-counting function, i.e. $π(n)$ is the number of primes $≤ n$.
+
+# --hints--
+
+`consecutiveDieThrows()` should return `653972374`.
+
+```js
+assert.strictEqual(consecutiveDieThrows(), 653972374);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function consecutiveDieThrows() {
+
+ return true;
+}
+
+consecutiveDieThrows();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-424-kakuro.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-424-kakuro.md
new file mode 100644
index 00000000000..90b1b38773f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-424-kakuro.md
@@ -0,0 +1,77 @@
+---
+id: 5900f5141000cf542c510026
+title: 'Problem 424: Kakuro'
+challengeType: 1
+forumTopicId: 302094
+dashedName: problem-424-kakuro
+---
+
+# --description--
+
+
+
+The above is an example of a cryptic kakuro (also known as cross sums, or even sums cross) puzzle, with its final solution on the right. (The common rules of kakuro puzzles can be found easily on numerous internet sites. Other related information can also be currently found at krazydad.com whose author has provided the puzzle data for this challenge.)
+
+The `testPuzzles` array contains the description of 200 such puzzles, a mix of 5x5 and 6x6 types. The first puzzle in the file is the above example which is coded as string as follows:
+
+`6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X`
+
+The first character is a numerical digit indicating the size of the information grid. It would be either a 6 (for a 5x5 kakuro puzzle) or a 7 (for a 6x6 puzzle) followed by a comma (,). The extra top line and left column are needed to insert information.
+
+The content of each cell is then described and followed by a comma, going left to right and starting with the top line.
+
+`X` = Gray cell, not required to be filled by a digit.
+
+`O` (upper case letter)= White empty cell to be filled by a digit.
+
+`A` = Or any one of the upper case letters from A to J to be replaced by its equivalent digit in the solved puzzle.
+
+`( )` = Location of the encrypted sums. Horizontal sums are preceded by a lower case "h" and vertical sums are preceded by a lower case "v". Those are followed by one or two upper case letters depending if the sum is a single digit or double digit one. For double digit sums, the first letter would be for the "tens" and the second one for the "units". When the cell must contain information for both a horizontal and a vertical sum, the first one is always for the horizontal sum and the two are separated by a comma within the same set of brackets, ex.: (hFE,vD). Each set of brackets is also immediately followed by a comma.
+
+The description of the last cell is followed by a Carriage Return/Line Feed (CRLF) instead of a comma.
+
+The required answer to each puzzle is based on the value of each letter necessary to arrive at the solution and according to the alphabetical order. As indicated under the example puzzle, its answer would be 8426039571. At least 9 out of the 10 encrypting letters are always part of the problem description. When only 9 are given, the missing one must be assigned the remaining digit.
+
+You are given that the sum of the answers for the first 10 puzzles in `testPuzzles` is 64414157580.
+
+Find the sum of the answers for `puzzles` array.
+
+# --hints--
+
+`kakuro(testPuzzles)` should return `1059760019628`.
+
+```js
+assert.strictEqual(kakuro(_testPuzzles), 1059760019628);
+```
+
+# --seed--
+
+
+## --after-user-code--
+
+```js
+const _testPuzzles = [
+ '6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X','7,X,X,X,X,(vJJ),(vCD),X,X,X,X,(hCG),O,O,(vCE),X,X,X,(hCI,vJB),C,O,O,X,(vB),(hJF,vJF),O,F,O,O,(hJA),F,G,O,O,X,X,(hCA),O,A,O,X,X,X,X,(hCF),O,O,X,X,X','7,X,X,X,(vE),(vCB),X,X,X,X,(hJ),O,O,(vCA),X,X,(vCH),(hCG,vCJ),O,O,O,(vJ),(hCE),O,O,O,(hJ,vGG),O,O,(hD),I,O,(hCD,vCB),H,O,O,X,(hCE),O,O,E,X,X,X,X,(hCE),O,O,X,X','6,X,X,X,(vEA),(vJF),X,X,X,(hI),O,O,(vJA),X,(vA),(hEI,vEB),O,O,O,(hIG),C,O,J,O,D,(hJD),O,O,O,X,X,X,(hJD),O,O,X,X','7,X,(vH),(vG),X,X,(vI),(vDH),(hG),B,O,(vDI),(hDB,vDE),O,O,(hBC),I,O,F,O,O,J,X,X,(hG),O,O,X,X,X,(vDG),(hH,vDD),O,O,(vDJ),(vC),(hBI),O,O,O,O,O,O,(hDJ),O,O,X,(hA),O,O','6,X,(vID),(vIJ),X,X,X,(hH),F,I,(vF),(vIA),X,(hIA),G,B,O,C,X,X,(hID),O,O,O,(vIF),X,(hIA),E,O,I,O,X,X,X,(hII),O,G','6,X,X,(vAF),(vAI),X,X,X,(hJ,vAC),O,B,(vGJ),X,(hGH),J,O,O,O,(vAF),(hAG),O,O,(hH,vF),A,D,X,(hGF),O,E,O,O,X,X,(hD),O,O,X','7,X,X,X,X,(vCE),(vGB),X,X,(vJG),(vCI),(hCD,vCJ),O,O,X,(hCI),O,O,O,O,B,(vJB),(hCF),O,O,O,(hCA,vH),O,O,(hCJ),O,O,(hJB,vCJ),O,O,O,X,(hJD),O,O,O,O,O,X,(hF),I,O,X,X,X','7,X,(vBB),(vBD),X,X,X,X,(hBB),C,E,(vEE),(vEC),X,X,(hBC),O,O,O,O,X,X,X,(hEF),H,O,A,(vJ),X,X,X,(hBD),O,O,O,(vI),X,X,(hBE),F,O,O,O,X,X,X,X,(hG),O,O','7,X,X,(vGG),(vGD),X,(vI),(vGI),X,(hGB),O,O,(hGH,vIC),O,O,X,(hGA),O,O,O,J,O,X,X,(hGI),O,O,X,X,X,(vGD),(hE,vE),O,O,(vGF),X,(hIH),O,O,O,O,O,X,(hE),A,O,(hGF),O,O,X','6,X,(vIJ),(vIE),X,X,X,(hF),O,C,(vIA),X,X,(hCA),O,O,D,(vIH),X,X,(hIB),E,O,O,(vF),X,X,(hD),O,A,O,X,X,X,(hID),O,G','6,X,(vAD),(vGI),(vI),X,X,(hB),O,O,O,(vAF),X,(hGC),O,O,O,O,(vGA),(hGE),O,O,(hJ,vB),O,O,X,(hGD),D,O,E,O,X,X,(hAI),O,C,O','6,X,X,X,(vAB),(vFA),X,X,X,(hHI),O,O,(vHJ),X,(vA),(hFJ,vHE),I,D,O,(hFH),O,O,O,O,O,(hHJ),O,O,O,X,X,X,(hC),O,J,X,X','7,X,X,X,(vJ),(vEF),X,X,X,X,(hI,vGD),C,E,(vEF),(vA),X,(hEH),O,O,O,O,O,X,(hH,vJ),O,O,(hJ,vEJ),O,O,(hD),O,A,(hEF,vEB),O,O,X,(hCC),O,O,A,O,O,X,X,X,(hH),O,O,X,X','7,X,X,X,(vAG),(vAJ),(vFH),X,X,X,(hFD),O,O,O,X,X,(vH),(hAJ,vAB),O,O,O,(vB),(hAH),O,H,O,(hC,vAI),O,O,(hE),O,O,(hAI,vAE),O,O,O,X,(hJ),O,O,O,X,X,X,(hFG),E,O,O,X,X','7,X,(vAI),(vHB),X,X,(vJE),(vAA),(hD),O,O,X,(hG),O,O,(hAJ),O,O,(vE),(hAA,vAI),O,O,X,(hHF),O,O,O,O,X,X,(hJF,vAE),O,O,O,J,(vH),(hAI),D,O,X,(hB),O,O,(hAG),O,O,X,(hAA),O,O','7,X,X,(vHJ),(vC),(vAF),X,X,X,(hHF),O,O,O,(vHI),(vHD),X,(hHB,vAB),O,O,O,O,E,(hAI),O,O,X,(hAB),O,O,(hD),O,O,(vAB),(hAI,vE),J,O,(hHH),O,O,O,B,O,X,X,X,(hG),O,A,O,X','6,X,X,(vDF),(vHE),X,X,X,(hHJ,vE),C,O,X,X,(hHI),O,O,O,(vDF),(vHH),(hFA),A,O,B,O,O,X,X,(hE),O,I,O,X,X,(hHH),O,O,X','6,X,(vA),(vA),X,X,X,(hE),O,O,(vCJ),X,X,(hG),O,O,O,(vHI),X,X,(hHC),O,O,H,(vB),X,X,(hCE),O,O,D,X,X,X,(hE),O,O','6,X,X,X,X,(vEH),(vEC),X,X,X,(hEB,vEJ),O,O,X,X,(hEC,vEF),O,O,B,X,(hDD,vEI),O,B,C,X,(hB),O,D,A,X,X,(hEC),O,O,X,X,X','6,X,X,X,X,(vIF),(vH),X,X,X,(hIJ,vGJ),B,I,X,X,(hIB,vIC),O,O,G,X,(hIA,vC),O,O,O,X,(hE),O,O,O,X,X,(hIA),E,O,X,X,X','7,X,(vC),(vFB),X,X,X,X,(hFH),O,O,(vFA),(vFJ),(vC),X,(hFJ),O,O,O,O,O,X,X,X,(hA,vJ),O,O,O,X,X,(hG),D,O,O,(vC),(vFC),X,(hBH),A,O,O,O,E,X,X,X,X,(hFH),O,I','6,X,X,(vFD),(vC),X,X,X,(hDH),E,F,(vDG),(vDD),X,(hDF,vDI),O,O,A,O,(hDG),O,O,(hDG,vDG),O,O,(hDJ),O,D,J,O,X,X,X,(hJ),E,O,X','6,X,X,X,(vE),(vGH),(vIC),X,X,(hD,vIG),O,O,A,X,(hIF,vJ),O,J,E,O,(hJ),O,D,(hGG,vGH),O,O,(hGG),O,O,O,O,X,(hIC),O,O,O,X,X','7,X,X,X,X,(vAG),(vJA),(vH),X,X,X,(hAJ,vDJ),O,O,O,X,X,(hJF),O,O,O,O,X,X,(hG),D,O,X,X,X,(vJH),(hJE,vJD),C,I,X,X,(hAE),B,O,O,O,X,X,(hAJ),O,O,E,X,X,X','7,X,X,X,X,(vGG),(vIA),(vGF),X,X,X,(hGF),O,O,D,X,X,X,(hGJ,vIB),O,O,O,X,X,(hGH,vGD),O,O,O,X,X,(hII,vC),O,J,O,X,X,(hIH),J,O,O,X,X,X,(hGE),O,I,O,X,X,X','6,X,X,(vFA),(vEC),X,X,X,(hI,vFI),F,O,X,X,(hDE),O,O,O,(vFF),(vFF),(hDI),G,J,O,F,O,X,X,(hFJ),O,D,O,X,X,(hFH),J,A,X','7,X,X,X,X,X,(vID),(vBB),X,X,X,X,(hBC),O,I,X,X,(vIH),(vBH),(hBF,vF),O,O,X,(hIE,vD),O,O,I,O,O,(hAG),O,O,O,O,F,X,(hA),O,O,X,X,X,X,(hD),O,O,X,X,X,X','7,X,(vCD),(vCC),X,X,X,X,(hE),B,C,(vCE),X,X,X,(hCD),O,O,O,(vE),(vCG),X,X,(hCH),O,O,O,O,X,X,(hFC),B,J,G,O,(vCC),X,X,X,(hCI),O,O,O,X,X,X,X,(hG),O,O','7,X,X,X,(vID),(vD),(vFB),X,X,X,(hIB,vID),O,O,O,X,X,(hJE,vIA),J,C,O,D,(vF),(hIB),O,O,X,(hIG),O,O,(hIJ),O,O,(vD),(hA,vID),O,O,X,(hJF),O,O,O,O,X,X,(hIE),O,O,O,X,X','7,X,X,(vAC),(vAH),X,X,X,X,(hD),O,O,(vAD),X,X,X,(hCH,vAD),O,O,O,(vAA),(vF),(hAC),O,H,(hAB,vAJ),O,O,A,(hAE),O,O,O,(hD,vAD),O,O,X,X,(hAC),O,O,O,X,X,X,X,(hG),O,O,X','6,X,X,(vBB),(vBE),X,X,X,(hBH),O,I,(vBG),(vBB),X,(hHE,vBD),H,D,O,O,(hBA),C,O,(hA,vG),O,O,(hBF),I,O,O,O,X,X,X,(hG),O,O,X','6,X,X,(vEC),(vD),X,X,X,(hD,vH),O,O,(vIB),X,(hIA),O,O,O,O,(vE),(hII),O,F,(hII,vIG),O,O,X,(hIH),O,O,O,O,X,X,(hIA),O,D,X','6,X,X,X,X,(vEH),(vEG),X,X,X,(hEB,vEF),O,O,X,X,(hAC,vG),O,B,O,X,(hEE,vEC),O,D,O,X,(hEE),O,O,O,X,X,(hEJ),D,O,X,X,X','6,X,(vD),(vB),X,X,X,(hA),O,O,(vE),X,X,(hE),A,O,O,(vCJ),X,X,(hCH),O,A,O,(vCI),X,X,(hB),O,D,O,X,X,X,(hCB),G,O','7,X,X,X,X,(vHJ),(vIF),(vIB),X,X,X,(hIH,vJI),O,O,J,X,X,(hIA),O,O,O,F,X,X,(hIG),O,C,X,X,X,(vD),(hA,vIB),O,J,X,X,(hHB),O,O,O,O,X,X,(hHB),O,O,O,X,X,X','7,X,X,X,(vBJ),(vIB),X,X,X,(vIF),(hBB,vBB),O,O,(vBA),X,(hIC),O,O,O,O,O,(vBA),(hBD),O,O,(hC,vC),O,O,O,(hBJ),E,O,O,(hBC,vBI),G,H,X,(hBA),O,O,O,O,O,X,X,(hBF),O,O,X,X','7,X,(vHI),(vHE),X,X,X,X,(hA),O,O,X,X,X,X,(hHG),O,O,(vHH),(vHE),(vIJ),X,(hHA),O,O,O,O,O,(vHI),X,(hID),H,O,O,B,I,X,X,X,X,(hHB),F,O,X,X,X,X,(hHE),O,H','6,X,X,(vAJ),(vAJ),X,X,X,(hAF,vAA),G,A,X,X,(hDA),O,O,O,(vDE),(vAH),(hAJ),O,O,O,O,I,X,X,(hAG),D,C,O,X,X,(hAI),O,O,X','6,X,X,X,X,(vDH),(vDA),X,X,X,(hG,vDG),O,E,X,X,(hBJ,vBC),O,O,O,X,(hBI,vE),O,E,O,X,(hE),O,O,O,X,X,(hDH),O,E,X,X,X','6,X,X,X,X,(vHJ),(vHH),X,X,X,(hHE,vCC),O,O,X,X,(hF,vG),A,O,O,X,(hHC,vHJ),O,B,O,X,(hHH),O,O,O,X,X,(hHI),O,O,X,X,X','7,X,(vJ),(vDG),X,X,(vDF),(vEF),(hC),E,B,X,(hEA),O,O,(hEE),C,O,(vH),(hED,vEF),A,O,X,(hEC),O,O,O,O,X,X,(hDD,vEF),O,O,O,O,(vEA),(hEJ),O,F,X,(hJ),O,O,(hEF),O,O,X,(hEF),O,O','7,X,X,X,(vCC),(vD),X,X,X,(vJE),(hI,vCH),O,O,(vBF),X,(hCC),O,O,O,O,A,(vJB),(hCB),G,O,O,(hJA,vJF),O,O,(hJA),O,O,(hG,vH),O,O,O,X,(hCE),O,O,O,O,O,X,X,(hH),O,O,X,X','7,X,X,(vEI),(vEB),(vG),X,X,X,(hEF),E,O,O,(vHE),X,X,(hEF,vH),O,O,O,O,(vEI),(hH),O,O,X,(hEH),O,B,(hG),O,O,(vG),(hEI,vED),O,O,X,(hAG),C,O,O,O,X,X,X,(hEE),O,O,O,X','6,X,X,X,X,(vJE),(vF),X,X,X,(hI,vJJ),O,O,X,X,(hEC,vJJ),H,O,O,X,(hF,vJB),O,O,O,X,(hJI),A,C,E,X,X,(hJD),O,J,X,X,X','6,X,X,X,(vH),(vAE),X,X,X,(hCB,vCJ),O,O,(vCB),X,(hCA,vD),O,O,O,O,(hD),C,O,(hCC,vJ),O,O,(hAB),A,O,F,O,X,X,(hB),G,O,X,X','6,X,X,(vEC),(vEG),X,X,X,(hEF),O,O,(vFC),(vEI),X,(hHJ,vJ),E,O,O,A,(hJ),O,O,(hEA,vEA),O,O,(hHH),O,O,O,B,X,X,X,(hEF),O,O,X','7,X,(vEI),(vEC),X,X,X,X,(hH),O,O,X,X,X,X,(hED),O,O,(vEB),(vEG),(vGB),X,(hEJ),O,O,O,O,O,(vD),X,(hIA),O,O,O,O,C,X,X,X,X,(hA),O,I,X,X,X,X,(hEB),A,O','7,X,X,X,(vF),(vG),(vIB),X,X,(vG),(hBA,vIH),J,I,D,X,(hBG),O,O,O,O,O,(vBG),(hA),O,O,X,(hE),O,O,(hBB),O,C,(vA),(hBI,vBE),O,O,X,(hBA),O,O,O,O,O,X,(hBF),O,O,O,X,X','7,X,X,(vEF),(vDI),X,X,X,X,(hDG),O,O,(vDA),X,X,X,(hEA,vG),O,O,O,(vEJ),(vJ),(hF),O,G,(hDH,vDI),O,O,F,(hED),O,O,O,(hDD,vB),O,O,X,X,(hDB),O,O,A,X,X,X,X,(hH),O,O,X','7,X,X,X,X,(vJH),(vD),(vAJ),X,X,X,(hAC,vDH),O,O,O,X,X,(hAA),O,O,O,O,X,X,(hC),F,O,X,X,X,(vC),(hAJ,vAA),I,H,X,X,(hJA),O,D,O,G,X,X,(hJB),O,C,O,X,X,X','6,X,X,X,(vDC),(vG),X,X,X,(hA),O,O,(vCH),X,(vCI),(hCB,vB),O,O,O,(hDF),O,H,O,O,O,(hH),O,O,O,X,X,X,(hH),J,O,X,X','6,X,X,(vCG),(vGA),X,X,X,(hE),O,O,(vGG),(vGB),X,(hCI,vF),O,O,O,I,(hGI),O,O,(hI,vD),O,A,(hGH),O,B,O,O,X,X,X,(hA),O,O,X','6,X,X,X,(vJ),(vHF),X,X,(vF),(hHG,vHD),O,A,X,(hHI),A,O,O,O,(vHE),(hB),G,O,(hD,vHE),O,F,X,(hGJ),O,O,O,O,X,(hHD),O,O,X,X','6,X,X,X,X,(vBD),(vD),X,X,X,(hD,vBB),O,O,X,X,(hI,vHD),O,O,O,X,(hHD,vBE),O,O,A,X,(hHF),C,O,G,X,X,(hBI),O,O,X,X,X','7,X,(vJ),(vFB),(vDB),X,X,X,(hFC),O,O,O,(vFE),X,X,(hFB),O,O,O,O,X,X,X,X,(hG),I,O,X,X,X,X,(hA),O,O,(vFG),(vE),X,X,(hDD),O,O,O,A,X,X,X,(hFD),D,E,J','6,X,X,X,(vAD),(vAH),X,X,(vB),(hF,vEB),O,O,X,(hED),O,O,O,O,(vD),(hD),O,O,(hJ,vI),O,O,X,(hEH),O,A,O,C,X,(hB),G,O,X,X','6,X,X,X,X,(vFG),(vFB),X,X,X,(hFD,vB),O,O,X,X,(hFG,vFG),O,O,O,X,(hI,vH),O,O,C,X,(hGA),E,H,O,X,X,(hD),O,G,X,X,X','7,X,X,X,(vBH),(vBB),X,X,X,X,(hBJ,vBJ),I,O,(vHE),(vI),X,(hBF,vBA),O,O,O,O,O,(hBE),O,D,X,(hA),O,O,(hBC),O,O,(vA),(hBB,vBH),O,O,(hDA),B,H,O,O,O,X,X,X,(hI),O,O,X,X','7,X,X,X,(vEC),(vD),X,X,X,(vJ),(hEB,vEJ),O,O,X,X,(hFC),O,O,O,F,(vEG),X,(hG),O,O,(hH,vFI),O,E,(vEH),X,(hEB),A,O,(hED,vJ),O,O,X,X,(hFI),O,O,O,O,X,X,(hED),O,O,X,X','6,X,(vGH),(vGG),X,X,X,(hGE),O,O,(vFI),(vGJ),X,(hGF),O,O,D,O,X,X,(hGB),O,C,O,(vGG),X,(hFG),O,O,O,O,X,X,X,(hE),O,I','7,X,X,X,(vF),(vGI),X,X,X,(vJ),(hB,vGA),H,G,X,X,(hHF),O,O,O,A,(vHH),X,(hB),O,O,(hGB,vGA),C,O,(vC),X,(hGC),O,O,(hGI,vGF),O,O,X,X,(hHB),O,E,O,O,X,X,(hA),O,O,X,X','7,X,X,X,X,X,(vED),(vIG),X,X,X,X,(hEC),O,O,X,X,(vAC),(vA),(hH,vEG),O,O,X,(hAE,vB),O,O,H,O,O,(hIJ),O,O,O,B,O,X,(hEC),O,O,X,X,X,X,(hEI),O,O,X,X,X,X','7,X,X,(vAI),(vAA),X,X,X,X,(hAD,vAG),O,O,(vAE),X,X,(hAH),O,O,O,O,(vBH),(vD),(hG),O,O,(hI,vE),O,O,O,(hAI),O,O,O,(hG,vAC),D,F,X,X,(hAH),O,O,O,O,X,X,X,(hAJ),O,O,X','7,X,X,(vGD),(vFB),(vJ),X,X,X,(hGD),O,O,O,(vFA),(vGG),X,(hFA),O,O,O,O,O,X,(hGE,vGF),O,O,(hH,vFB),O,O,(hH),O,G,(hGC,vD),O,G,X,(hEB),O,O,O,O,O,X,X,X,(hGC),O,A,O,X','6,X,X,(vAD),(vEE),X,X,X,(hEC),G,O,(vAJ),(vH),X,(hEC,vEG),O,A,O,O,(hEG),F,O,(hEG,vEG),O,O,(hAB),O,E,F,A,X,X,X,(hEG),O,O,X','6,X,X,X,X,(vIB),(vJ),X,X,X,(hB,vIJ),O,O,X,X,(hE,vIF),O,O,C,X,(hFC,vIF),O,A,O,X,(hG),O,O,H,X,X,(hIJ),O,O,X,X,X','6,X,X,X,(vIB),(vEB),X,X,X,(hD,vAE),O,O,(vE),X,(hIJ,vE),O,O,O,O,(hII),O,O,(hJ,vC),H,O,(hAE),O,O,G,J,X,X,(hC),O,O,X,X','6,X,X,(vFF),(vB),X,X,X,(hC,vI),O,J,(vJE),X,(hJJ),O,O,I,G,(vA),(hJJ),O,O,(hJD,vJE),O,O,X,(hJB),O,O,F,O,X,X,(hJH),C,J,X','7,X,X,X,(vEI),(vJI),X,X,X,X,(hJA),O,O,(vJE),(vJJ),X,X,(hJI,vJB),O,E,O,D,X,(hJI,vC),O,H,(hJB,vJE),O,O,(hB),O,O,(hF,vD),O,O,X,(hJB),O,O,O,O,X,X,X,X,(hJE),O,O,X,X','7,X,(vJB),(vFD),X,X,(vFE),(vH),(hJF),O,O,X,(hH),O,O,(hJC),O,O,(vH),(hJF,vJF),O,O,X,(hJI),H,O,O,O,X,X,(hFJ,vJJ),J,O,O,O,(vJA),(hA),G,O,X,(hJF),O,C,(hJC),O,O,X,(hD),O,O','7,X,(vI),(vDH),X,X,X,X,(hB),O,I,X,X,X,X,(hC),O,O,(vA),(vI),(vDJ),X,(hDH),O,B,O,O,O,(vDH),X,(hGG),O,O,O,J,O,X,X,X,X,(hHH),B,O,X,X,X,X,(hHE),O,O','6,X,X,(vDI),(vE),X,X,X,(hA,vDA),E,O,(vHI),X,(hHI),F,A,O,O,(vDF),(hDD),O,O,(hDJ,vDJ),O,O,X,(hDG),O,O,H,O,X,X,(hB),O,D,X','6,X,(vJ),(vDH),X,X,X,(hDA),G,O,(vDA),(vDB),X,(hDB),O,O,I,F,X,X,(hG),O,F,O,(vDI),X,(hED),G,O,O,F,X,X,X,(hDE),O,H','6,X,X,(vCJ),(vD),X,X,X,(hG),O,O,(vAD),(vAE),X,(hCC,vI),O,O,A,O,(hJ),O,F,(hAD,vAD),I,H,(hCD),O,O,O,F,X,X,X,(hAJ),O,G,X','7,X,X,X,X,(vEF),(vEC),(vF),X,X,X,(hED,vEB),O,O,O,X,X,(hEB),O,O,O,O,X,X,(hC),O,D,X,X,X,(vI),(hB,vEE),O,O,X,X,(hEB),E,H,D,O,X,X,(hHJ),O,G,O,X,X,X','7,X,X,X,X,(vJF),(vIC),X,X,X,(vIA),(hD,vJE),O,O,X,X,(hIJ,vD),J,O,O,D,(vG),(hJC),I,O,O,(hJA,vC),O,O,(hJF),J,C,(hJF,vJE),O,O,O,X,(hIB),O,O,O,O,X,X,(hJF),O,O,X,X,X','6,X,(vH),(vJE),X,X,X,(hC),J,O,(vJJ),(vJC),X,(hJJ),A,I,O,H,X,X,(hD),O,O,A,(vC),X,(hAI),F,B,O,O,X,X,X,(hC),J,O','7,X,(vA),(vEE),X,X,(vD),(vF),(hEC),O,O,(vIH),(hI,vEB),O,O,(hBD),O,O,O,O,F,O,X,X,(hA),O,O,X,X,X,(vJ),(hEJ,vEG),F,O,(vA),(vG),(hBG),O,O,O,O,O,O,(hEH),O,O,X,(hG),O,O','6,X,X,X,(vFG),(vFC),X,X,(vE),(hFE,vFF),A,O,X,(hBF),O,O,O,O,(vH),(hE),O,O,(hD,vFF),I,O,X,(hFF),O,O,E,D,X,(hFI),O,O,X,X','6,X,X,(vHA),(vFH),X,X,X,(hFF),O,O,(vFH),(vE),X,(hDI,vFG),O,O,O,O,(hFG),B,O,(hC,vFB),O,O,(hDC),O,G,O,F,X,X,X,(hFF),O,O,X','7,X,X,(vBE),(vBB),(vA),X,X,X,(hH),O,O,O,(vBA),(vH),X,(hGI,vBB),O,J,O,O,O,(hBG),O,O,X,(hI),O,O,(hC),O,O,(vBG),(hE,vBD),H,C,(hBI),O,O,O,O,O,X,X,X,(hGG),O,O,O,X','7,X,X,X,X,X,(vHC),(vF),X,X,X,X,(hF,vC),O,E,X,X,(vEJ),(hEF,vEG),F,O,H,X,(hHD),C,O,O,O,X,X,(hHC,vI),A,O,O,O,X,(hJ),D,O,O,X,X,X,(hF),O,O,X,X,X,X','6,X,X,(vH),(vDC),X,X,X,(hCI,vCD),O,O,X,X,(hH),O,O,O,(vCA),(vCB),(hCJ),O,I,O,D,E,X,X,(hDI),E,H,O,X,X,(hG),O,O,X','7,X,X,X,X,(vJ),(vHE),X,X,X,X,(hHA,vHF),O,B,(vHE),X,X,(hEC,vHG),O,O,O,O,X,(hHE,vHG),O,O,(hA,vHB),O,O,(hJ),O,O,(hHE,vJ),O,O,X,(hED),O,J,O,O,X,X,X,(hB),O,O,X,X,X','6,X,X,(vJG),(vA),X,X,X,(hI),B,O,(vJC),(vJH),X,(hJH,vJC),O,E,O,O,(hB),O,O,(hJJ,vF),O,O,(hCE),O,O,D,I,X,X,X,(hB),O,H,X','6,X,X,X,X,(vDG),(vHH),X,X,(vDH),(hJ,vHB),O,O,X,(hJF),O,O,O,O,X,(hHF,vE),O,O,O,X,(hDJ),H,O,O,I,X,(hHC),G,O,X,X,X','7,X,(vAI),(vHC),X,X,X,X,(hD),O,G,X,X,(vHI),(vG),(hAJ),O,O,(vB),(hH,vAH),O,O,X,(hHF,vH),O,O,F,O,O,(hCA),O,O,O,O,O,(vF),(hH),O,O,X,(hG),O,O,X,X,X,X,(hAH),O,O','7,X,X,X,X,(vFG),(vFI),X,X,X,X,(hFI,vFB),O,O,(vFJ),X,(vFA),(hFG,vGA),O,B,O,O,(hIB),O,O,O,(hH,vJ),O,O,(hJ),O,O,(hFD,vD),O,C,O,(hII),O,O,O,O,X,X,X,(hE),O,O,X,X,X','7,X,X,X,(vI),(vEG),(vFD),X,X,(vED),(hA,vEB),O,O,O,X,(hJC),O,O,A,O,O,X,(hEG),O,O,(hEG,vEC),O,O,(vB),X,(hH),O,O,(hJ,vEB),O,O,X,(hEI),O,O,O,O,J,X,(hFF),O,H,O,X,X','6,X,X,(vEI),(vEB),X,X,X,(hEC,vB),O,O,(vEB),X,(hHC),J,O,O,F,(vEC),(hH),O,O,(hB,vEC),O,O,X,(hEH),O,O,O,O,X,X,(hEA),D,O,X','6,X,X,(vAF),(vBF),X,X,X,(hBI),O,G,(vAD),(vBD),X,(hBI,vF),O,J,O,E,(hBB),A,G,(hBI,vBI),O,H,(hAJ),B,O,O,O,X,X,X,(hBA),O,O,X','6,X,(vCB),(vJ),X,X,X,(hCE),A,O,(vCI),X,X,(hCG),D,O,O,(vCC),X,X,(hCA),O,O,O,(vB),X,X,(hB),O,E,G,X,X,X,(hG),O,H','7,X,X,X,X,X,(vFI),(vHG),X,X,X,X,(hHJ,vHH),O,O,X,X,(vHC),(hHD,vHG),O,O,O,X,(hHH),O,O,O,O,X,X,(hFE,vHC),O,O,O,D,X,(hHE),H,O,O,X,X,X,(hHE),I,A,X,X,X,X','7,X,X,(vFA),(vC),X,X,X,X,(hE),O,B,(vAC),(vGJ),X,X,(hFF,vG),O,O,O,O,(vAI),(hAA),O,D,(hAB,vAC),O,O,O,(hAH),O,O,O,(hAB,vAB),O,O,X,(hFJ),O,O,O,O,X,X,X,X,(hAH),O,J,X','7,X,X,X,(vIF),(vIB),X,X,X,X,(hID),O,O,(vC),X,X,(vIF),(hIH,vEE),O,O,O,(vII),(hEB),O,O,O,(hIB,vIF),D,J,(hIF),O,O,(hII,vIE),O,O,O,X,(hJ),O,G,O,X,X,X,X,(hIF),O,O,X,X','7,X,(vDJ),(vDB),X,X,X,X,(hDJ),O,O,(vDF),(vCE),(vI),X,(hCH),O,O,O,O,O,X,X,X,(hDC,vDB),O,A,G,X,X,(hFE),O,O,O,(vDJ),(vI),X,(hCF),O,O,O,O,O,X,X,X,X,(hDE),O,O','6,X,X,(vCI),(vJ),X,X,X,(hA),O,E,(vEG),(vCC),X,(hEG,vCF),O,O,D,O,(hJ),C,G,(hB,vCC),C,O,(hED),O,O,A,O,X,X,X,(hCD),O,O,X','6,X,X,X,(vG),(vFE),X,X,X,(hG,vBC),O,O,(vBC),X,(hFJ,vC),O,E,O,I,(hG),O,O,(hBF,vBC),O,O,(hEJ),O,O,O,O,X,X,(hBA),D,O,X,X','6,X,X,(vAJ),(vE),X,X,X,(hFH,vH),O,O,(vFA),X,(hFH),O,O,O,O,(vFI),(hI),O,C,(hFI,vFD),O,O,X,(hAC),O,O,I,G,X,X,(hC),O,O,X','6,X,X,X,(vE),(vCJ),X,X,(vFF),(hA,vHJ),C,O,X,(hFC),O,O,O,F,(vD),(hFI),O,O,(hFE,vFJ),O,O,X,(hFG),O,O,O,O,X,(hFD),O,O,X,X','7,X,X,X,(vBJ),(vBI),X,X,X,X,(hA),O,O,(vCH),(vBJ),X,(vCJ),(hCB,vG),H,O,I,B,(hBA),O,O,O,(hBE,vG),O,O,(hBB),F,O,(hBE,vBI),O,O,O,(hBI),O,O,O,O,X,X,X,X,(hBC),O,O,X,X','6,X,X,(vCJ),(vD),X,X,X,(hH),O,O,(vBD),(vJ),X,(hCI,vCH),O,J,F,O,(hCG),O,E,(hA,vCD),O,F,(hBF),O,O,O,O,X,X,X,(hCG),O,O,X','6,X,X,X,X,(vJB),(vG),X,X,X,(hA,vH),I,O,X,X,(hCD,vCG),O,O,B,X,(hCF,vCD),O,O,O,X,(hJD),O,H,O,X,X,(hB),O,O,X,X,X','7,X,(vI),(vEH),X,X,(vCC),(vF),(hG),O,O,X,(hH),O,C,(hJ),O,O,(vAD),(hAG,vG),O,O,X,(hEI),F,O,O,O,X,X,(hAD,vAB),O,O,I,O,(vI),(hG),O,O,X,(hC),O,O,(hAJ),O,O,X,(hAA),O,O','7,X,X,X,X,X,(vEC),(vEA),X,X,X,X,(hB),O,O,X,X,(vDF),(vEH),(hEC,vH),H,O,X,(hEA,vI),O,B,E,O,O,(hDB),E,J,O,D,O,X,(hEH),O,A,X,X,X,X,(hI),O,O,X,X,X,X','6,X,X,X,(vBC),(vBC),X,X,X,(hBJ,vEC),H,O,(vBB),X,(hBE,vA),D,J,O,O,(hC),O,O,(hBE,vBG),O,O,(hEG),H,O,B,O,X,X,(hBI),O,O,X,X','7,X,(vE),(vCF),X,X,X,X,(hJ),O,O,(vFB),X,X,X,(hCJ),O,O,A,(vFE),(vCA),X,X,(hIH),O,O,O,O,X,X,(hFF),O,O,O,B,(vFA),X,X,X,(hCI),O,O,O,X,X,X,X,(hFG),O,O','7,X,X,X,X,(vBH),(vH),X,X,X,X,(hI),O,O,(vE),X,X,X,(hJG,vBF),O,O,O,X,(vH),(hBA,vJE),O,O,O,O,(hDG),O,O,O,O,X,X,(hBG),O,F,O,X,X,X,X,(hA),J,O,X,X,X','7,X,X,X,X,X,(vIC),(vA),X,X,X,(vII),(hG,vIH),F,I,X,X,(hIG),O,O,O,D,X,X,(hC,vC),O,O,J,X,X,(hIF,vE),O,G,A,X,X,(hIH),O,O,O,O,X,X,(hJ),F,D,X,X,X,X','7,X,X,X,(vH),(vCJ),X,X,X,(vCG),(hCB,vEG),O,O,X,X,(hEF),O,I,O,O,(vCI),X,(hCD),O,J,(hCB,vCJ),E,O,(vCC),X,(hCE),O,O,(hCI,vH),O,O,X,X,(hEB),O,O,O,O,X,X,(hD),O,O,X,X','6,X,(vGA),(vBE),X,X,X,(hGC),H,O,(vGF),X,X,(hGG),O,O,O,(vGD),X,X,(hBG),O,J,O,(vGD),X,X,(hGD),O,O,E,X,X,X,(hGH),O,O','6,X,X,(vEE),(vEJ),X,X,X,(hI,vEF),O,O,(vEH),X,(hEA),O,O,O,E,(vB),(hEE),O,O,(hB,vB),O,O,X,(hEG),A,O,I,O,X,X,(hA),D,B,X','6,X,(vJ),(vHA),X,X,X,(hHH),D,O,(vHG),X,X,(hI),O,O,F,(vDG),X,X,(hDJ),O,O,O,(vHF),X,X,(hHF),O,O,E,X,X,X,(hHE),B,O','6,X,X,X,X,(vFI),(vE),X,X,X,(hH,vA),J,I,X,X,(hGF,vD),O,O,F,X,(hGF,vC),O,O,A,X,(hD),O,O,O,X,X,(hD),O,O,X,X,X','7,X,X,(vHG),(vE),X,X,X,X,(hGD),O,O,(vGA),(vHC),(vAJ),X,(hGD,vAC),O,O,O,O,O,(hGC),O,O,(hAA,vGC),O,O,O,(hAC),O,O,F,(hGD,vD),O,O,(hHB),O,O,O,O,O,X,X,X,X,(hI),O,D,X','7,X,X,(vBG),(vBJ),X,(vBD),(vE),X,(hC),O,O,(hBB,vAG),O,C,X,(hBE),O,O,O,O,D,X,(hBG),O,O,O,(vBE),X,X,(vE),(hBI,vJ),O,O,O,X,(hCG),F,G,O,O,O,X,(hC),O,O,(hBJ),O,O,X','7,X,X,X,X,X,(vEA),(vJJ),X,X,(vED),(vJI),(hF),O,O,X,(hB),O,O,(hJH,vB),O,O,X,(hED),O,B,O,O,X,X,(hJI,vJI),O,O,C,O,X,(hJH),O,O,(hJJ),O,O,X,(hF),J,E,X,X,X,X','6,X,(vF),(vED),X,X,X,(hEI),O,O,(vEA),X,X,(hEJ),O,O,J,(vB),X,X,(hB),O,O,O,(vG),X,X,(hJ),B,O,C,X,X,X,(hF),O,E','6,X,X,X,X,(vCH),(vCD),X,X,X,(hG,vCH),O,O,X,X,(hCH,vCI),O,O,O,X,(hFA,vCE),O,O,J,X,(hFF),O,O,O,X,X,(hI),F,C,X,X,X','6,X,X,(vCH),(vA),X,X,X,(hE,vE),D,O,(vAG),(vHC),(hHB),O,O,C,O,I,(hHA),O,O,(hE,vJ),O,O,(hCH),A,O,O,O,O,X,X,(hHD),O,O,X','7,X,(vF),(vDG),(vGD),X,X,X,(hA),O,D,O,(vI),(vGE),X,(hDG),O,C,O,O,O,X,(hGC),H,O,(hH,vA),O,O,(vGF),X,(hH),O,O,(hGB,vGD),O,O,X,(hDH),O,D,O,O,O,X,X,X,(hA),O,O,G','7,X,X,X,X,(vIG),(vIG),X,X,X,X,(hCJ),O,O,(vCE),X,X,X,(hIE,vEA),O,O,O,X,(vJ),(hEA,vIE),O,O,O,O,(hCH),O,F,O,O,X,X,(hCH),I,B,O,X,X,X,X,(hCH),O,O,X,X,X','7,X,X,X,X,(vJ),(vDB),X,X,X,X,(hDG,vH),O,O,X,X,(vB),(hJ,vEB),E,O,O,(vG),(hDJ),O,F,D,(hI,vDC),O,O,(hA),O,O,(hJ,vA),O,O,I,X,(hDA),O,O,O,X,X,X,(hDH),O,O,X,X,X','6,X,X,X,(vEE),(vJA),(vEI),X,X,(hD,vEE),O,F,O,X,(hED,vEC),O,O,O,O,(hJ),O,O,(hEH,vEI),O,O,(hIB),O,O,O,O,X,(hII),O,O,O,X,X','6,X,(vE),(vGH),X,X,X,(hC),O,J,(vFJ),X,X,(hGH),O,O,O,(vJ),X,X,(hFA),B,O,I,(vFF),X,X,(hFG),O,O,O,X,X,X,(hB),F,G','6,X,X,(vIF),(vIJ),X,X,X,(hD,vIC),O,O,X,X,(hIB),O,O,O,(vIG),(vA),(hBF),O,O,F,I,O,X,X,(hE),D,O,F,X,X,(hIF),O,C,X','7,X,(vCD),(vB),X,X,X,X,(hII),O,D,(vA),X,X,X,(hIJ),O,O,O,(vII),X,X,(hID),O,O,O,O,(vIJ),(vCJ),X,X,(hCA),H,O,F,O,X,X,X,(hA),O,O,G,X,X,X,X,(hII),J,O','7,X,(vC),(vFF),X,X,(vHF),(vD),(hFD),O,O,(vHG),(hA,vFJ),O,O,(hHF),O,O,O,O,O,O,X,X,(hFG,vFH),O,O,O,X,X,(hFB,vI),O,O,O,(vFB),(vB),(hIG),O,O,O,O,D,J,(hG),O,I,X,(hFE),O,O','7,X,(vHJ),(vDE),X,X,(vDI),(vHH),(hHG),O,J,(vHJ),(hJ),O,O,(hHE),O,O,O,(hHJ,vB),O,O,X,(hHH),O,O,O,O,X,X,(hDJ,vHA),D,O,E,O,(vF),(hHJ),O,O,(hA),O,O,E,(hHA),O,O,X,(hI),O,O','7,X,(vEH),(vFA),X,X,X,X,(hEB),O,O,(vFA),X,X,X,(hFD),O,O,O,(vEE),(vID),X,X,(hFB),O,O,O,O,X,X,(hFJ),O,O,O,O,(vEE),X,X,X,(hJ),O,B,O,X,X,X,X,(hEH),C,O','6,X,(vJ),(vE),X,X,X,(hA),B,C,(vCJ),X,X,(hCG),O,O,O,(vCD),X,X,(hHF),O,O,O,(vJ),X,X,(hE),O,O,H,X,X,X,(hCE),O,O','6,X,(vGC),(vGH),X,X,X,(hGG),O,O,(vGB),X,X,(hGI),E,O,I,(vGG),X,X,(hIJ),O,C,O,(vA),X,X,(hD),G,O,O,X,X,X,(hD),O,O','6,X,X,X,X,(vIG),(vII),X,X,X,(hE,vIA),I,G,X,X,(hGJ,vGF),O,C,O,X,(hIE,vII),D,O,O,X,(hGJ),O,B,O,X,X,(hA),O,J,X,X,X','6,X,X,X,X,(vIA),(vE),X,X,(vJB),(hB,vII),I,J,X,(hIF),O,O,O,H,X,(hIB,vG),D,J,O,X,(hJG),C,O,O,F,X,(hB),O,O,X,X,X','7,X,X,X,(vDB),(vGG),X,X,X,X,(hGH),O,O,(vGA),(vGA),X,X,(hGF,vGA),O,O,O,O,X,(hGA,vGE),B,O,(hGD,vI),O,O,(hJ),O,I,(hGE,vGG),O,O,X,(hDA),O,D,O,O,X,X,X,X,(hF),O,O,X,X','6,X,X,X,(vFB),(vI),X,X,X,(hGF),O,O,(vGA),X,(vH),(hGA,vFD),O,O,O,(hFF),O,A,O,O,C,(hGG),O,J,O,X,X,X,(hGH),O,D,X,X','6,X,X,(vGA),(vA),X,X,X,(hB,vGE),O,O,(vHJ),X,(hBD),O,O,O,O,(vGH),(hGC),O,O,(hGJ,vGE),O,O,X,(hGG),O,F,O,O,X,X,(hGC),O,O,X','7,X,X,(vCE),(vG),(vI),X,X,X,(hEE),A,O,E,(vCD),(vCH),X,(hEG,vCD),O,O,O,O,O,(hA),G,C,X,(hEH),O,O,(hEE),O,O,(vI),(hA,vD),O,O,(hCF),O,O,O,O,O,X,X,X,(hED),O,O,B,X','7,X,(vG),(vDC),X,(vBA),(vDG),X,(hJ),O,G,(hDA,vBA),O,O,X,(hBC),O,O,G,O,O,X,X,(hDH),O,O,O,(vG),X,X,X,(hG,vDI),O,O,O,(vJ),X,(hBB),E,O,O,O,O,X,(hH),O,J,(hB),O,O','6,X,X,X,(vJG),(vCG),X,X,(vJG),(hJB,vJH),O,O,X,(hJH),I,B,O,O,(vD),(hJB),O,O,(hA,vJG),O,O,X,(hJB),O,B,O,O,X,(hF),I,C,X,X','7,X,(vA),(vE),X,X,(vD),(vB),(hF),O,O,(vJJ),(hI,vGD),O,O,(hGD),O,O,O,O,I,O,X,X,(hJI),O,O,X,X,X,(vJE),(hA,vF),I,O,(vD),(vJJ),(hGA),O,O,O,J,O,O,(hH),O,O,X,(hI),O,O','7,X,X,(vEH),(vEF),X,X,X,X,(hEI,vIH),O,O,(vEI),X,X,(hEI),O,O,O,O,(vIE),(vEJ),(hD),O,O,(hEH,vH),O,O,O,(hEC),O,O,O,(hD,vC),H,G,X,X,(hIA),O,O,O,O,X,X,X,(hD),E,O,X','7,X,X,X,X,X,(vEA),(vCJ),X,X,X,X,(hCD,vCC),O,O,X,X,(vCI),(hCJ,vEH),O,O,O,X,(hDH),O,J,B,O,X,X,(hCH,vD),O,O,O,O,X,(hCJ),O,O,O,X,X,X,(hJ),O,G,X,X,X,X','7,X,(vB),(vFF),X,(vEI),(vFE),X,(hH),O,O,(hFC,vIB),G,O,X,(hFC),O,O,O,O,O,X,X,X,(hFH),O,D,X,X,X,X,(hFF,vFG),O,O,(vFE),(vFH),X,(hEE),O,O,J,O,O,X,(hFG),O,O,(hFG),O,O','6,X,(vHE),(vII),X,X,X,(hHB),O,O,(vHF),(vHJ),X,(hHD),B,O,O,O,X,X,(hG),H,O,O,(vHE),X,(hCA),O,O,E,B,X,X,X,(hHB),O,G','6,X,(vH),(vAF),X,X,X,(hAC),O,O,(vAD),X,X,(hDI),J,O,O,(vAH),X,X,(hAC),O,O,O,(vAI),X,X,(hH),O,O,B,X,X,X,(hAH),O,E','6,X,(vC),(vHA),X,X,X,(hC),O,J,(vHA),X,X,(hF),J,O,O,(vHC),X,X,(hI),O,J,O,(vF),X,X,(hEJ),O,O,B,X,X,X,(hG),O,O','6,X,X,X,(vFJ),(vJC),X,X,(vFF),(hFF,vJE),O,O,X,(hFH),O,F,O,O,(vD),(hFI),O,C,(hE,vH),D,O,X,(hJC),O,O,O,A,X,(hFG),O,J,X,X','7,X,X,X,X,X,(vDE),(vBB),X,(vC),(vDF),X,(hBF),O,O,(hH),O,O,(vE),(hH,vBI),B,O,(hDF),O,O,O,O,D,(vE),X,(hDI,vBE),O,O,C,O,B,(hBF),O,A,X,(hG),E,D,(hG),O,O,X,X,X,X','7,X,(vJ),(vFH),X,X,X,X,(hHH),F,A,X,X,(vGE),(vA),(hI),O,O,(vC),(hF,vD),O,O,X,(hHC,vF),H,O,O,O,O,(hGJ),O,O,O,O,O,(vE),(hE),O,O,X,(hHI),O,O,X,X,X,X,(hA),O,O','7,X,X,(vCD),(vCB),(vF),X,X,X,(hCA,vCJ),O,O,O,(vFH),X,(hCD),O,O,O,O,O,(vCB),(hH),O,O,X,(hI),O,O,(hCE),O,B,(vCE),(hCH,vCI),O,G,X,(hFA),O,G,O,O,O,X,X,(hBC),H,O,O,X','6,X,X,X,X,(vHD),(vHH),X,X,X,(hA,vHH),H,I,X,X,(hHJ,vIG),O,C,O,X,(hHC,vE),O,O,O,X,(hIG),J,O,O,X,X,(hHF),O,O,X,X,X','6,X,X,(vFD),(vJB),X,X,X,(hH,vH),O,O,(vJD),X,(hFH),O,O,O,O,(vJI),(hJD),O,O,(hJD,vG),J,E,X,(hJD),O,O,O,O,X,X,(hB),A,O,X','6,X,X,X,(vC),(vDC),X,X,(vF),(hHB,vDI),O,O,(vDJ),(hDG),O,O,E,O,O,(hHA),O,O,(hHD,vG),O,O,(hEJ),O,O,F,O,O,X,(hJ),O,O,X,X','7,X,X,X,X,X,(vEJ),(vG),X,X,X,X,(hD,vI),C,O,X,X,(vEG),(hFE,vFE),O,O,O,X,(hFD),O,O,O,O,X,X,(hEC,vFI),O,O,O,O,X,(hEC),B,O,H,X,X,X,(hJ),O,O,X,X,X,X','7,X,(vI),(vAC),X,X,(vAI),(vCG),(hB),O,I,X,(hCB,vCD),O,O,(hH),A,D,(hCD,vAF),O,O,O,X,(hAC),O,O,O,O,X,X,(hCF,vCC),O,O,O,O,(vB),(hCB),O,O,O,(hCF),O,O,(hCB),O,J,X,(hB),O,O','6,X,X,X,(vJB),(vIG),X,X,(vA),(hJI,vJC),O,F,X,(hJB),O,O,O,O,(vJE),(hJD),B,O,(hJB,vD),O,H,X,(hJG),O,I,O,O,X,(hA),O,E,X,X','7,X,X,X,X,(vCD),(vCC),(vB),X,X,X,(hCC,vEC),O,I,O,X,X,(hCH),C,O,O,O,X,X,(hCA),F,O,X,X,X,(vA),(hCH,vCE),O,E,X,X,(hGA),C,O,O,O,X,X,(hCE),O,O,O,X,X,X','6,X,X,X,X,(vJI),(vA),X,X,(vJH),(hJE,vJI),O,G,X,(hJE),F,O,O,D,X,(hC,vB),O,E,O,X,(hJH),O,O,O,O,X,(hJD),O,E,X,X,X','6,X,X,X,X,(vAJ),(vAJ),X,X,X,(hAF,vGB),O,O,X,X,(hAE,vD),O,O,O,X,(hAJ,vF),O,J,O,X,(hAF),O,O,H,X,X,(hB),O,I,X,X,X','7,X,X,X,X,(vH),(vIE),X,X,X,X,(hA,vA),O,O,X,X,(vID),(hF,vCH),O,O,A,(vIE),(hIH),O,O,O,(hIA,vIH),O,O,(hIE),O,O,(hIG,vIA),B,O,O,X,(hIF),O,G,A,X,X,X,(hIE),O,D,X,X,X','7,X,(vEF),(vB),(vFC),X,X,X,(hH),O,O,O,(vEA),X,X,(hED),C,O,O,O,X,X,X,X,(hEG),O,F,X,X,X,X,(hEI),O,O,(vEH),(vI),X,X,(hFH),O,O,O,O,X,X,X,(hEE),O,I,O','6,X,(vHI),(vDG),X,X,X,(hHE),J,O,(vDG),X,X,(hHC),H,O,O,(vHA),X,X,(hDH),F,O,G,(vHE),X,X,(hHC),O,O,O,X,X,X,(hHE),O,O','6,X,X,(vAD),(vAE),X,X,X,(hAA),O,O,(vAD),(vAA),X,(hAI,vI),O,F,D,J,(hC),A,O,(hB,vJ),A,E,(hAB),O,I,C,J,X,X,X,(hI),O,H,X','6,X,X,(vDA),(vE),X,X,X,(hJ,vDE),O,F,(vGG),X,(hDJ),O,O,O,O,(vC),(hDD),O,O,(hJ,vI),O,O,X,(hGG),O,D,O,O,X,X,(hDA),G,B,X','7,X,X,(vJD),(vG),(vI),X,X,X,(hG),O,O,H,(vEB),(vEF),X,(hEB),O,O,B,O,J,X,(hEJ,vA),O,H,(hEE,vEA),O,O,(hA),O,O,(hEJ,vG),O,O,X,(hJF),O,O,O,O,O,X,X,X,(hG),F,O,O,X','6,X,X,X,X,(vEJ),(vG),X,X,X,(hDE,vF),O,O,X,X,(hDJ,vF),O,O,O,X,(hA,vDA),O,O,O,X,(hDI),B,O,O,X,X,(hDE),C,O,X,X,X','6,X,X,(vAC),(vD),X,X,X,(hD,vEI),O,O,(vBC),X,(hBA),O,O,O,O,(vH),(hEF),O,O,(hEI,vF),O,O,X,(hEF),O,O,A,O,X,X,(hEE),G,D,X','6,X,X,(vGB),(vD),X,X,X,(hGG),A,C,(vGJ),(vC),X,(hGG,vGC),O,O,O,J,(hGH),O,O,(hE,vI),G,H,(hHF),O,H,O,O,X,X,X,(hE),O,O,X','6,X,X,(vIJ),(vCD),X,X,X,(hCD),O,O,(vCI),(vCG),X,(hIH,vCC),G,O,O,O,(hCE),O,I,(hCH,vCD),G,O,(hIC),B,D,O,O,X,X,X,(hA),O,O,X','7,X,(vII),(vDH),(vID),X,X,X,(hIG),O,O,O,X,X,X,(hDA),O,C,J,(vII),X,X,X,(hID),F,O,O,(vDH),X,X,X,(hID),O,O,O,(vID),X,X,X,(hIE),A,O,O,X,X,X,(hDD),O,O,O','7,X,(vEB),(vF),X,X,X,X,(hED),O,O,(vAJ),(vED),(vD),X,(hIB),O,O,O,G,O,X,X,X,(hF,vA),O,O,O,X,X,(hED),O,O,F,(vA),(vEB),X,(hIE),O,H,O,O,O,X,X,X,X,(hEE),O,O','7,X,X,X,X,(vCA),(vCE),(vB),X,X,X,(hF),O,O,O,X,X,X,(hJG,vCD),I,O,O,X,X,(hF,vB),O,O,O,X,X,(hJI,vCI),O,F,O,X,X,(hD),O,O,O,X,X,X,(hCI),O,O,O,X,X,X','6,X,(vJI),(vI),X,X,X,(hH),O,O,(vD),X,X,(hJA),F,O,O,(vJH),X,X,(hJI),C,G,O,(vJJ),X,X,(hD),O,O,O,X,X,X,(hJE),O,O','6,X,X,X,(vDC),(vAE),X,X,X,(hI),O,B,(vI),X,(vC),(hJ,vDE),O,O,O,(hAF),A,D,O,O,O,(hI),O,O,G,X,X,X,(hDA),H,O,X,X','7,X,X,X,(vFD),(vAF),X,X,X,(vFD),(hFE,vFA),B,O,X,X,(hHI),O,O,O,O,(vFF),X,(hFI),O,O,(hC,vG),O,H,(vFA),X,(hE),O,O,(hFB,vC),O,O,X,X,(hFJ),O,G,O,O,X,X,(hH),O,O,X,X','7,X,X,X,X,(vD),(vHD),X,X,X,(vDH),(hA,vJJ),O,O,(vE),X,(hHB,vJH),O,O,O,E,J,(hJE),H,O,O,(hD,vF),O,O,(hJG),E,O,(hJE,vJG),C,O,O,(hHH),J,O,O,O,O,X,X,(hJJ),O,O,X,X,X','7,X,X,X,X,(vBA),(vEB),X,X,X,(vBG),(hC,vBB),O,O,X,X,(hBD,vBA),O,O,O,O,(vBJ),(hBC),O,O,O,(hBG,vBD),A,O,(hBB),O,O,(hEE,vBF),O,O,D,X,(hBJ),O,O,O,I,X,X,(hBD),O,O,X,X,X','7,X,X,X,X,X,(vDG),(vC),X,(vB),(vFH),X,(hC),E,O,(hA),O,O,(vDD),(hH,vDB),O,O,(hDA),C,O,O,O,O,(vE),X,(hFH,vDE),O,O,H,O,F,(hDH),O,O,X,(hDI),O,O,(hJ),O,O,X,X,X,X','6,X,(vB),(vE),X,X,X,(hA),D,O,(vA),X,X,(hH),O,C,O,(vIG),X,X,(hDI),O,O,O,(vDF),X,X,(hIF),O,O,O,X,X,X,(hH),O,O','7,X,(vHF),(vC),X,X,(vC),(vHF),(hC),O,O,(vBC),(hA,vBF),O,O,(hBE),O,O,O,O,O,O,X,X,(hHD),A,O,X,X,X,(vD),(hJ,vHA),O,O,(vHI),(vC),(hCH),J,O,O,O,O,B,(hHH),O,O,X,(hE),O,O','6,X,X,X,(vJ),(vDA),X,X,(vFD),(hB,vFE),O,O,(vDA),(hDJ),O,O,O,O,O,(hDE),O,O,(hDA,vC),O,H,(hBA),O,I,O,G,O,X,(hJ),E,O,X,X','6,X,(vGA),(vA),X,X,X,(hGE),O,O,(vGD),X,X,(hGA),O,G,A,(vED),X,X,(hGE),O,O,O,(vGD),X,X,(hEB),C,H,F,X,X,X,(hGE),A,I','6,X,(vIC),(vFD),X,X,X,(hIG),O,C,(vIB),X,X,(hFJ),O,O,O,(vII),X,X,(hIE),O,O,F,(vIA),X,X,(hIJ),F,I,O,X,X,X,(hIC),O,O','6,X,X,X,(vJG),(vHH),X,X,X,(hHA),O,O,(vHD),X,(vE),(hJF,vHJ),O,O,O,(hHB),F,O,D,O,O,(hE),O,J,O,X,X,X,(hHE),I,O,X,X','7,X,X,X,(vGG),(vI),(vEC),X,X,(vBH),(hJ,vBI),O,O,O,X,(hBJ),O,O,O,O,O,(vJ),(hGJ),O,O,X,(hA),O,O,(hGC),O,O,(vC),(hGB,vGJ),O,O,X,(hBF),O,O,O,O,B,X,(hBH),O,O,O,X,X','7,X,X,X,X,X,(vD),(vHB),X,X,(vG),(vFC),(hHA,vAI),O,O,X,(hAB),O,O,O,O,O,X,(hAD),O,O,O,(vHB),X,X,(vF),(hAF,vHI),O,O,O,X,(hAB),O,O,O,O,O,X,(hB),O,E,X,X,X,X','6,X,(vBC),(vDF),X,X,X,(hBE),O,O,(vDB),X,X,(hDG),O,J,O,(vC),X,X,(hBI),O,O,O,(vBB),X,X,(hBA),O,O,D,X,X,X,(hBG),F,O','6,X,X,X,(vH),(vDC),(vGA),X,X,(hA,vIE),O,O,O,X,(hIG,vGG),O,O,O,O,(hF),O,O,(hGF,vJ),J,O,(hGA),O,O,O,O,X,(hIE),O,O,O,X,X','6,X,(vHC),(vHJ),X,X,X,(hHC),A,B,(vA),X,X,(hHI),O,O,O,(vHA),X,X,(hD),F,O,O,(vB),X,X,(hII),G,O,O,X,X,X,(hB),O,O','7,X,(vH),(vJA),X,X,(vIE),(vJI),(hJC),O,O,(vDG),(hJE,vIG),O,O,(hDD),I,O,O,O,O,O,X,X,(hII,vIG),O,O,O,X,X,(hIE,vJA),O,O,O,(vB),(vJI),(hDG),C,O,O,O,O,O,(hJF),O,O,X,(hH),O,O','7,X,(vHH),(vBE),X,X,X,X,(hE),B,O,X,(vHF),(vBJ),X,(hHI),C,O,(hJ,vHI),O,O,X,X,(hBC),D,O,O,O,X,X,(hHH),O,O,D,O,(vHF),X,(hHD),F,O,(hHD),G,O,X,X,X,X,(hHE),O,O','7,X,X,X,X,X,(vIF),(vI),X,X,X,X,(hB,vGF),O,O,X,X,(vEG),(hGG,vB),O,O,O,X,(hGJ),O,O,O,H,X,X,(hGA,vA),O,O,O,O,X,(hGC),I,H,O,X,X,X,(hH),G,J,X,X,X,X','7,X,X,X,X,X,(vJF),(vJF),X,X,X,X,(hJD),A,O,X,X,(vBG),(vJB),(hI,vI),O,O,X,(hBD,vJF),F,O,O,E,O,(hIB),O,O,O,O,C,X,(hJG),O,B,X,X,X,X,(hI),O,J,X,X,X,X','6,X,X,(vEI),(vC),X,X,X,(hH,vGG),O,O,(vGD),X,(hBJ),O,O,O,O,(vD),(hGI),O,O,(hD,vD),E,G,X,(hBG),O,O,A,O,X,X,(hJ),O,O,X','7,X,X,X,X,(vFI),(vJF),X,X,X,X,(hJH),O,O,(vJC),X,X,X,(hEE,vEC),O,O,O,X,(vJE),(hED,vEF),O,O,O,G,(hJB),O,O,O,O,X,X,(hEH),O,O,G,X,X,X,X,(hJG),O,O,X,X,X','7,X,X,X,(vJ),(vEI),X,X,X,X,(hJ,vEC),O,A,(vBD),X,X,(hHC,vEA),O,O,O,I,(vF),(hEE),O,O,(hEE,vHD),B,J,O,(hHE),O,O,O,(hG,vED),O,O,X,(hHD),O,O,O,O,X,X,X,(hEA),O,O,X,X','7,X,X,X,X,X,(vFH),(vED),X,X,X,X,(hEC,vEA),O,O,X,X,(vED),(hFI,vEH),O,O,O,X,(hEE),O,O,A,D,X,X,(hFB,vJ),O,O,O,J,X,(hFI),O,O,O,X,X,X,(hI),O,A,X,X,X,X','6,X,(vB),(vHI),X,X,X,(hHH),O,O,(vHJ),(vGA),X,(hHH),O,O,O,I,X,X,(hGE),O,A,O,(vHE),X,(hHJ),H,B,F,D,X,X,X,(hHJ),O,C'
+]
+```
+
+## --seed-contents--
+
+```js
+function kakuro(puzzles) {
+
+ return true;
+}
+
+const testPuzzles = [
+ '6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X','7,X,X,X,X,(vJJ),(vCD),X,X,X,X,(hCG),O,O,(vCE),X,X,X,(hCI,vJB),C,O,O,X,(vB),(hJF,vJF),O,F,O,O,(hJA),F,G,O,O,X,X,(hCA),O,A,O,X,X,X,X,(hCF),O,O,X,X,X','7,X,X,X,(vE),(vCB),X,X,X,X,(hJ),O,O,(vCA),X,X,(vCH),(hCG,vCJ),O,O,O,(vJ),(hCE),O,O,O,(hJ,vGG),O,O,(hD),I,O,(hCD,vCB),H,O,O,X,(hCE),O,O,E,X,X,X,X,(hCE),O,O,X,X','6,X,X,X,(vEA),(vJF),X,X,X,(hI),O,O,(vJA),X,(vA),(hEI,vEB),O,O,O,(hIG),C,O,J,O,D,(hJD),O,O,O,X,X,X,(hJD),O,O,X,X','7,X,(vH),(vG),X,X,(vI),(vDH),(hG),B,O,(vDI),(hDB,vDE),O,O,(hBC),I,O,F,O,O,J,X,X,(hG),O,O,X,X,X,(vDG),(hH,vDD),O,O,(vDJ),(vC),(hBI),O,O,O,O,O,O,(hDJ),O,O,X,(hA),O,O','6,X,(vID),(vIJ),X,X,X,(hH),F,I,(vF),(vIA),X,(hIA),G,B,O,C,X,X,(hID),O,O,O,(vIF),X,(hIA),E,O,I,O,X,X,X,(hII),O,G','6,X,X,(vAF),(vAI),X,X,X,(hJ,vAC),O,B,(vGJ),X,(hGH),J,O,O,O,(vAF),(hAG),O,O,(hH,vF),A,D,X,(hGF),O,E,O,O,X,X,(hD),O,O,X','7,X,X,X,X,(vCE),(vGB),X,X,(vJG),(vCI),(hCD,vCJ),O,O,X,(hCI),O,O,O,O,B,(vJB),(hCF),O,O,O,(hCA,vH),O,O,(hCJ),O,O,(hJB,vCJ),O,O,O,X,(hJD),O,O,O,O,O,X,(hF),I,O,X,X,X','7,X,(vBB),(vBD),X,X,X,X,(hBB),C,E,(vEE),(vEC),X,X,(hBC),O,O,O,O,X,X,X,(hEF),H,O,A,(vJ),X,X,X,(hBD),O,O,O,(vI),X,X,(hBE),F,O,O,O,X,X,X,X,(hG),O,O','7,X,X,(vGG),(vGD),X,(vI),(vGI),X,(hGB),O,O,(hGH,vIC),O,O,X,(hGA),O,O,O,J,O,X,X,(hGI),O,O,X,X,X,(vGD),(hE,vE),O,O,(vGF),X,(hIH),O,O,O,O,O,X,(hE),A,O,(hGF),O,O,X','6,X,(vIJ),(vIE),X,X,X,(hF),O,C,(vIA),X,X,(hCA),O,O,D,(vIH),X,X,(hIB),E,O,O,(vF),X,X,(hD),O,A,O,X,X,X,(hID),O,G','6,X,(vAD),(vGI),(vI),X,X,(hB),O,O,O,(vAF),X,(hGC),O,O,O,O,(vGA),(hGE),O,O,(hJ,vB),O,O,X,(hGD),D,O,E,O,X,X,(hAI),O,C,O','6,X,X,X,(vAB),(vFA),X,X,X,(hHI),O,O,(vHJ),X,(vA),(hFJ,vHE),I,D,O,(hFH),O,O,O,O,O,(hHJ),O,O,O,X,X,X,(hC),O,J,X,X','7,X,X,X,(vJ),(vEF),X,X,X,X,(hI,vGD),C,E,(vEF),(vA),X,(hEH),O,O,O,O,O,X,(hH,vJ),O,O,(hJ,vEJ),O,O,(hD),O,A,(hEF,vEB),O,O,X,(hCC),O,O,A,O,O,X,X,X,(hH),O,O,X,X','7,X,X,X,(vAG),(vAJ),(vFH),X,X,X,(hFD),O,O,O,X,X,(vH),(hAJ,vAB),O,O,O,(vB),(hAH),O,H,O,(hC,vAI),O,O,(hE),O,O,(hAI,vAE),O,O,O,X,(hJ),O,O,O,X,X,X,(hFG),E,O,O,X,X','7,X,(vAI),(vHB),X,X,(vJE),(vAA),(hD),O,O,X,(hG),O,O,(hAJ),O,O,(vE),(hAA,vAI),O,O,X,(hHF),O,O,O,O,X,X,(hJF,vAE),O,O,O,J,(vH),(hAI),D,O,X,(hB),O,O,(hAG),O,O,X,(hAA),O,O','7,X,X,(vHJ),(vC),(vAF),X,X,X,(hHF),O,O,O,(vHI),(vHD),X,(hHB,vAB),O,O,O,O,E,(hAI),O,O,X,(hAB),O,O,(hD),O,O,(vAB),(hAI,vE),J,O,(hHH),O,O,O,B,O,X,X,X,(hG),O,A,O,X','6,X,X,(vDF),(vHE),X,X,X,(hHJ,vE),C,O,X,X,(hHI),O,O,O,(vDF),(vHH),(hFA),A,O,B,O,O,X,X,(hE),O,I,O,X,X,(hHH),O,O,X','6,X,(vA),(vA),X,X,X,(hE),O,O,(vCJ),X,X,(hG),O,O,O,(vHI),X,X,(hHC),O,O,H,(vB),X,X,(hCE),O,O,D,X,X,X,(hE),O,O','6,X,X,X,X,(vEH),(vEC),X,X,X,(hEB,vEJ),O,O,X,X,(hEC,vEF),O,O,B,X,(hDD,vEI),O,B,C,X,(hB),O,D,A,X,X,(hEC),O,O,X,X,X','6,X,X,X,X,(vIF),(vH),X,X,X,(hIJ,vGJ),B,I,X,X,(hIB,vIC),O,O,G,X,(hIA,vC),O,O,O,X,(hE),O,O,O,X,X,(hIA),E,O,X,X,X','7,X,(vC),(vFB),X,X,X,X,(hFH),O,O,(vFA),(vFJ),(vC),X,(hFJ),O,O,O,O,O,X,X,X,(hA,vJ),O,O,O,X,X,(hG),D,O,O,(vC),(vFC),X,(hBH),A,O,O,O,E,X,X,X,X,(hFH),O,I','6,X,X,(vFD),(vC),X,X,X,(hDH),E,F,(vDG),(vDD),X,(hDF,vDI),O,O,A,O,(hDG),O,O,(hDG,vDG),O,O,(hDJ),O,D,J,O,X,X,X,(hJ),E,O,X','6,X,X,X,(vE),(vGH),(vIC),X,X,(hD,vIG),O,O,A,X,(hIF,vJ),O,J,E,O,(hJ),O,D,(hGG,vGH),O,O,(hGG),O,O,O,O,X,(hIC),O,O,O,X,X','7,X,X,X,X,(vAG),(vJA),(vH),X,X,X,(hAJ,vDJ),O,O,O,X,X,(hJF),O,O,O,O,X,X,(hG),D,O,X,X,X,(vJH),(hJE,vJD),C,I,X,X,(hAE),B,O,O,O,X,X,(hAJ),O,O,E,X,X,X','7,X,X,X,X,(vGG),(vIA),(vGF),X,X,X,(hGF),O,O,D,X,X,X,(hGJ,vIB),O,O,O,X,X,(hGH,vGD),O,O,O,X,X,(hII,vC),O,J,O,X,X,(hIH),J,O,O,X,X,X,(hGE),O,I,O,X,X,X','6,X,X,(vFA),(vEC),X,X,X,(hI,vFI),F,O,X,X,(hDE),O,O,O,(vFF),(vFF),(hDI),G,J,O,F,O,X,X,(hFJ),O,D,O,X,X,(hFH),J,A,X','7,X,X,X,X,X,(vID),(vBB),X,X,X,X,(hBC),O,I,X,X,(vIH),(vBH),(hBF,vF),O,O,X,(hIE,vD),O,O,I,O,O,(hAG),O,O,O,O,F,X,(hA),O,O,X,X,X,X,(hD),O,O,X,X,X,X','7,X,(vCD),(vCC),X,X,X,X,(hE),B,C,(vCE),X,X,X,(hCD),O,O,O,(vE),(vCG),X,X,(hCH),O,O,O,O,X,X,(hFC),B,J,G,O,(vCC),X,X,X,(hCI),O,O,O,X,X,X,X,(hG),O,O','7,X,X,X,(vID),(vD),(vFB),X,X,X,(hIB,vID),O,O,O,X,X,(hJE,vIA),J,C,O,D,(vF),(hIB),O,O,X,(hIG),O,O,(hIJ),O,O,(vD),(hA,vID),O,O,X,(hJF),O,O,O,O,X,X,(hIE),O,O,O,X,X','7,X,X,(vAC),(vAH),X,X,X,X,(hD),O,O,(vAD),X,X,X,(hCH,vAD),O,O,O,(vAA),(vF),(hAC),O,H,(hAB,vAJ),O,O,A,(hAE),O,O,O,(hD,vAD),O,O,X,X,(hAC),O,O,O,X,X,X,X,(hG),O,O,X','6,X,X,(vBB),(vBE),X,X,X,(hBH),O,I,(vBG),(vBB),X,(hHE,vBD),H,D,O,O,(hBA),C,O,(hA,vG),O,O,(hBF),I,O,O,O,X,X,X,(hG),O,O,X','6,X,X,(vEC),(vD),X,X,X,(hD,vH),O,O,(vIB),X,(hIA),O,O,O,O,(vE),(hII),O,F,(hII,vIG),O,O,X,(hIH),O,O,O,O,X,X,(hIA),O,D,X','6,X,X,X,X,(vEH),(vEG),X,X,X,(hEB,vEF),O,O,X,X,(hAC,vG),O,B,O,X,(hEE,vEC),O,D,O,X,(hEE),O,O,O,X,X,(hEJ),D,O,X,X,X','6,X,(vD),(vB),X,X,X,(hA),O,O,(vE),X,X,(hE),A,O,O,(vCJ),X,X,(hCH),O,A,O,(vCI),X,X,(hB),O,D,O,X,X,X,(hCB),G,O','7,X,X,X,X,(vHJ),(vIF),(vIB),X,X,X,(hIH,vJI),O,O,J,X,X,(hIA),O,O,O,F,X,X,(hIG),O,C,X,X,X,(vD),(hA,vIB),O,J,X,X,(hHB),O,O,O,O,X,X,(hHB),O,O,O,X,X,X','7,X,X,X,(vBJ),(vIB),X,X,X,(vIF),(hBB,vBB),O,O,(vBA),X,(hIC),O,O,O,O,O,(vBA),(hBD),O,O,(hC,vC),O,O,O,(hBJ),E,O,O,(hBC,vBI),G,H,X,(hBA),O,O,O,O,O,X,X,(hBF),O,O,X,X','7,X,(vHI),(vHE),X,X,X,X,(hA),O,O,X,X,X,X,(hHG),O,O,(vHH),(vHE),(vIJ),X,(hHA),O,O,O,O,O,(vHI),X,(hID),H,O,O,B,I,X,X,X,X,(hHB),F,O,X,X,X,X,(hHE),O,H','6,X,X,(vAJ),(vAJ),X,X,X,(hAF,vAA),G,A,X,X,(hDA),O,O,O,(vDE),(vAH),(hAJ),O,O,O,O,I,X,X,(hAG),D,C,O,X,X,(hAI),O,O,X','6,X,X,X,X,(vDH),(vDA),X,X,X,(hG,vDG),O,E,X,X,(hBJ,vBC),O,O,O,X,(hBI,vE),O,E,O,X,(hE),O,O,O,X,X,(hDH),O,E,X,X,X','6,X,X,X,X,(vHJ),(vHH),X,X,X,(hHE,vCC),O,O,X,X,(hF,vG),A,O,O,X,(hHC,vHJ),O,B,O,X,(hHH),O,O,O,X,X,(hHI),O,O,X,X,X','7,X,(vJ),(vDG),X,X,(vDF),(vEF),(hC),E,B,X,(hEA),O,O,(hEE),C,O,(vH),(hED,vEF),A,O,X,(hEC),O,O,O,O,X,X,(hDD,vEF),O,O,O,O,(vEA),(hEJ),O,F,X,(hJ),O,O,(hEF),O,O,X,(hEF),O,O','7,X,X,X,(vCC),(vD),X,X,X,(vJE),(hI,vCH),O,O,(vBF),X,(hCC),O,O,O,O,A,(vJB),(hCB),G,O,O,(hJA,vJF),O,O,(hJA),O,O,(hG,vH),O,O,O,X,(hCE),O,O,O,O,O,X,X,(hH),O,O,X,X','7,X,X,(vEI),(vEB),(vG),X,X,X,(hEF),E,O,O,(vHE),X,X,(hEF,vH),O,O,O,O,(vEI),(hH),O,O,X,(hEH),O,B,(hG),O,O,(vG),(hEI,vED),O,O,X,(hAG),C,O,O,O,X,X,X,(hEE),O,O,O,X','6,X,X,X,X,(vJE),(vF),X,X,X,(hI,vJJ),O,O,X,X,(hEC,vJJ),H,O,O,X,(hF,vJB),O,O,O,X,(hJI),A,C,E,X,X,(hJD),O,J,X,X,X','6,X,X,X,(vH),(vAE),X,X,X,(hCB,vCJ),O,O,(vCB),X,(hCA,vD),O,O,O,O,(hD),C,O,(hCC,vJ),O,O,(hAB),A,O,F,O,X,X,(hB),G,O,X,X','6,X,X,(vEC),(vEG),X,X,X,(hEF),O,O,(vFC),(vEI),X,(hHJ,vJ),E,O,O,A,(hJ),O,O,(hEA,vEA),O,O,(hHH),O,O,O,B,X,X,X,(hEF),O,O,X','7,X,(vEI),(vEC),X,X,X,X,(hH),O,O,X,X,X,X,(hED),O,O,(vEB),(vEG),(vGB),X,(hEJ),O,O,O,O,O,(vD),X,(hIA),O,O,O,O,C,X,X,X,X,(hA),O,I,X,X,X,X,(hEB),A,O','7,X,X,X,(vF),(vG),(vIB),X,X,(vG),(hBA,vIH),J,I,D,X,(hBG),O,O,O,O,O,(vBG),(hA),O,O,X,(hE),O,O,(hBB),O,C,(vA),(hBI,vBE),O,O,X,(hBA),O,O,O,O,O,X,(hBF),O,O,O,X,X','7,X,X,(vEF),(vDI),X,X,X,X,(hDG),O,O,(vDA),X,X,X,(hEA,vG),O,O,O,(vEJ),(vJ),(hF),O,G,(hDH,vDI),O,O,F,(hED),O,O,O,(hDD,vB),O,O,X,X,(hDB),O,O,A,X,X,X,X,(hH),O,O,X','7,X,X,X,X,(vJH),(vD),(vAJ),X,X,X,(hAC,vDH),O,O,O,X,X,(hAA),O,O,O,O,X,X,(hC),F,O,X,X,X,(vC),(hAJ,vAA),I,H,X,X,(hJA),O,D,O,G,X,X,(hJB),O,C,O,X,X,X','6,X,X,X,(vDC),(vG),X,X,X,(hA),O,O,(vCH),X,(vCI),(hCB,vB),O,O,O,(hDF),O,H,O,O,O,(hH),O,O,O,X,X,X,(hH),J,O,X,X','6,X,X,(vCG),(vGA),X,X,X,(hE),O,O,(vGG),(vGB),X,(hCI,vF),O,O,O,I,(hGI),O,O,(hI,vD),O,A,(hGH),O,B,O,O,X,X,X,(hA),O,O,X','6,X,X,X,(vJ),(vHF),X,X,(vF),(hHG,vHD),O,A,X,(hHI),A,O,O,O,(vHE),(hB),G,O,(hD,vHE),O,F,X,(hGJ),O,O,O,O,X,(hHD),O,O,X,X','6,X,X,X,X,(vBD),(vD),X,X,X,(hD,vBB),O,O,X,X,(hI,vHD),O,O,O,X,(hHD,vBE),O,O,A,X,(hHF),C,O,G,X,X,(hBI),O,O,X,X,X','7,X,(vJ),(vFB),(vDB),X,X,X,(hFC),O,O,O,(vFE),X,X,(hFB),O,O,O,O,X,X,X,X,(hG),I,O,X,X,X,X,(hA),O,O,(vFG),(vE),X,X,(hDD),O,O,O,A,X,X,X,(hFD),D,E,J','6,X,X,X,(vAD),(vAH),X,X,(vB),(hF,vEB),O,O,X,(hED),O,O,O,O,(vD),(hD),O,O,(hJ,vI),O,O,X,(hEH),O,A,O,C,X,(hB),G,O,X,X','6,X,X,X,X,(vFG),(vFB),X,X,X,(hFD,vB),O,O,X,X,(hFG,vFG),O,O,O,X,(hI,vH),O,O,C,X,(hGA),E,H,O,X,X,(hD),O,G,X,X,X','7,X,X,X,(vBH),(vBB),X,X,X,X,(hBJ,vBJ),I,O,(vHE),(vI),X,(hBF,vBA),O,O,O,O,O,(hBE),O,D,X,(hA),O,O,(hBC),O,O,(vA),(hBB,vBH),O,O,(hDA),B,H,O,O,O,X,X,X,(hI),O,O,X,X','7,X,X,X,(vEC),(vD),X,X,X,(vJ),(hEB,vEJ),O,O,X,X,(hFC),O,O,O,F,(vEG),X,(hG),O,O,(hH,vFI),O,E,(vEH),X,(hEB),A,O,(hED,vJ),O,O,X,X,(hFI),O,O,O,O,X,X,(hED),O,O,X,X','6,X,(vGH),(vGG),X,X,X,(hGE),O,O,(vFI),(vGJ),X,(hGF),O,O,D,O,X,X,(hGB),O,C,O,(vGG),X,(hFG),O,O,O,O,X,X,X,(hE),O,I','7,X,X,X,(vF),(vGI),X,X,X,(vJ),(hB,vGA),H,G,X,X,(hHF),O,O,O,A,(vHH),X,(hB),O,O,(hGB,vGA),C,O,(vC),X,(hGC),O,O,(hGI,vGF),O,O,X,X,(hHB),O,E,O,O,X,X,(hA),O,O,X,X','7,X,X,X,X,X,(vED),(vIG),X,X,X,X,(hEC),O,O,X,X,(vAC),(vA),(hH,vEG),O,O,X,(hAE,vB),O,O,H,O,O,(hIJ),O,O,O,B,O,X,(hEC),O,O,X,X,X,X,(hEI),O,O,X,X,X,X','7,X,X,(vAI),(vAA),X,X,X,X,(hAD,vAG),O,O,(vAE),X,X,(hAH),O,O,O,O,(vBH),(vD),(hG),O,O,(hI,vE),O,O,O,(hAI),O,O,O,(hG,vAC),D,F,X,X,(hAH),O,O,O,O,X,X,X,(hAJ),O,O,X','7,X,X,(vGD),(vFB),(vJ),X,X,X,(hGD),O,O,O,(vFA),(vGG),X,(hFA),O,O,O,O,O,X,(hGE,vGF),O,O,(hH,vFB),O,O,(hH),O,G,(hGC,vD),O,G,X,(hEB),O,O,O,O,O,X,X,X,(hGC),O,A,O,X','6,X,X,(vAD),(vEE),X,X,X,(hEC),G,O,(vAJ),(vH),X,(hEC,vEG),O,A,O,O,(hEG),F,O,(hEG,vEG),O,O,(hAB),O,E,F,A,X,X,X,(hEG),O,O,X','6,X,X,X,X,(vIB),(vJ),X,X,X,(hB,vIJ),O,O,X,X,(hE,vIF),O,O,C,X,(hFC,vIF),O,A,O,X,(hG),O,O,H,X,X,(hIJ),O,O,X,X,X','6,X,X,X,(vIB),(vEB),X,X,X,(hD,vAE),O,O,(vE),X,(hIJ,vE),O,O,O,O,(hII),O,O,(hJ,vC),H,O,(hAE),O,O,G,J,X,X,(hC),O,O,X,X','6,X,X,(vFF),(vB),X,X,X,(hC,vI),O,J,(vJE),X,(hJJ),O,O,I,G,(vA),(hJJ),O,O,(hJD,vJE),O,O,X,(hJB),O,O,F,O,X,X,(hJH),C,J,X','7,X,X,X,(vEI),(vJI),X,X,X,X,(hJA),O,O,(vJE),(vJJ),X,X,(hJI,vJB),O,E,O,D,X,(hJI,vC),O,H,(hJB,vJE),O,O,(hB),O,O,(hF,vD),O,O,X,(hJB),O,O,O,O,X,X,X,X,(hJE),O,O,X,X','7,X,(vJB),(vFD),X,X,(vFE),(vH),(hJF),O,O,X,(hH),O,O,(hJC),O,O,(vH),(hJF,vJF),O,O,X,(hJI),H,O,O,O,X,X,(hFJ,vJJ),J,O,O,O,(vJA),(hA),G,O,X,(hJF),O,C,(hJC),O,O,X,(hD),O,O','7,X,(vI),(vDH),X,X,X,X,(hB),O,I,X,X,X,X,(hC),O,O,(vA),(vI),(vDJ),X,(hDH),O,B,O,O,O,(vDH),X,(hGG),O,O,O,J,O,X,X,X,X,(hHH),B,O,X,X,X,X,(hHE),O,O','6,X,X,(vDI),(vE),X,X,X,(hA,vDA),E,O,(vHI),X,(hHI),F,A,O,O,(vDF),(hDD),O,O,(hDJ,vDJ),O,O,X,(hDG),O,O,H,O,X,X,(hB),O,D,X','6,X,(vJ),(vDH),X,X,X,(hDA),G,O,(vDA),(vDB),X,(hDB),O,O,I,F,X,X,(hG),O,F,O,(vDI),X,(hED),G,O,O,F,X,X,X,(hDE),O,H','6,X,X,(vCJ),(vD),X,X,X,(hG),O,O,(vAD),(vAE),X,(hCC,vI),O,O,A,O,(hJ),O,F,(hAD,vAD),I,H,(hCD),O,O,O,F,X,X,X,(hAJ),O,G,X','7,X,X,X,X,(vEF),(vEC),(vF),X,X,X,(hED,vEB),O,O,O,X,X,(hEB),O,O,O,O,X,X,(hC),O,D,X,X,X,(vI),(hB,vEE),O,O,X,X,(hEB),E,H,D,O,X,X,(hHJ),O,G,O,X,X,X','7,X,X,X,X,(vJF),(vIC),X,X,X,(vIA),(hD,vJE),O,O,X,X,(hIJ,vD),J,O,O,D,(vG),(hJC),I,O,O,(hJA,vC),O,O,(hJF),J,C,(hJF,vJE),O,O,O,X,(hIB),O,O,O,O,X,X,(hJF),O,O,X,X,X','6,X,(vH),(vJE),X,X,X,(hC),J,O,(vJJ),(vJC),X,(hJJ),A,I,O,H,X,X,(hD),O,O,A,(vC),X,(hAI),F,B,O,O,X,X,X,(hC),J,O','7,X,(vA),(vEE),X,X,(vD),(vF),(hEC),O,O,(vIH),(hI,vEB),O,O,(hBD),O,O,O,O,F,O,X,X,(hA),O,O,X,X,X,(vJ),(hEJ,vEG),F,O,(vA),(vG),(hBG),O,O,O,O,O,O,(hEH),O,O,X,(hG),O,O','6,X,X,X,(vFG),(vFC),X,X,(vE),(hFE,vFF),A,O,X,(hBF),O,O,O,O,(vH),(hE),O,O,(hD,vFF),I,O,X,(hFF),O,O,E,D,X,(hFI),O,O,X,X','6,X,X,(vHA),(vFH),X,X,X,(hFF),O,O,(vFH),(vE),X,(hDI,vFG),O,O,O,O,(hFG),B,O,(hC,vFB),O,O,(hDC),O,G,O,F,X,X,X,(hFF),O,O,X','7,X,X,(vBE),(vBB),(vA),X,X,X,(hH),O,O,O,(vBA),(vH),X,(hGI,vBB),O,J,O,O,O,(hBG),O,O,X,(hI),O,O,(hC),O,O,(vBG),(hE,vBD),H,C,(hBI),O,O,O,O,O,X,X,X,(hGG),O,O,O,X','7,X,X,X,X,X,(vHC),(vF),X,X,X,X,(hF,vC),O,E,X,X,(vEJ),(hEF,vEG),F,O,H,X,(hHD),C,O,O,O,X,X,(hHC,vI),A,O,O,O,X,(hJ),D,O,O,X,X,X,(hF),O,O,X,X,X,X','6,X,X,(vH),(vDC),X,X,X,(hCI,vCD),O,O,X,X,(hH),O,O,O,(vCA),(vCB),(hCJ),O,I,O,D,E,X,X,(hDI),E,H,O,X,X,(hG),O,O,X','7,X,X,X,X,(vJ),(vHE),X,X,X,X,(hHA,vHF),O,B,(vHE),X,X,(hEC,vHG),O,O,O,O,X,(hHE,vHG),O,O,(hA,vHB),O,O,(hJ),O,O,(hHE,vJ),O,O,X,(hED),O,J,O,O,X,X,X,(hB),O,O,X,X,X','6,X,X,(vJG),(vA),X,X,X,(hI),B,O,(vJC),(vJH),X,(hJH,vJC),O,E,O,O,(hB),O,O,(hJJ,vF),O,O,(hCE),O,O,D,I,X,X,X,(hB),O,H,X','6,X,X,X,X,(vDG),(vHH),X,X,(vDH),(hJ,vHB),O,O,X,(hJF),O,O,O,O,X,(hHF,vE),O,O,O,X,(hDJ),H,O,O,I,X,(hHC),G,O,X,X,X','7,X,(vAI),(vHC),X,X,X,X,(hD),O,G,X,X,(vHI),(vG),(hAJ),O,O,(vB),(hH,vAH),O,O,X,(hHF,vH),O,O,F,O,O,(hCA),O,O,O,O,O,(vF),(hH),O,O,X,(hG),O,O,X,X,X,X,(hAH),O,O','7,X,X,X,X,(vFG),(vFI),X,X,X,X,(hFI,vFB),O,O,(vFJ),X,(vFA),(hFG,vGA),O,B,O,O,(hIB),O,O,O,(hH,vJ),O,O,(hJ),O,O,(hFD,vD),O,C,O,(hII),O,O,O,O,X,X,X,(hE),O,O,X,X,X','7,X,X,X,(vI),(vEG),(vFD),X,X,(vED),(hA,vEB),O,O,O,X,(hJC),O,O,A,O,O,X,(hEG),O,O,(hEG,vEC),O,O,(vB),X,(hH),O,O,(hJ,vEB),O,O,X,(hEI),O,O,O,O,J,X,(hFF),O,H,O,X,X','6,X,X,(vEI),(vEB),X,X,X,(hEC,vB),O,O,(vEB),X,(hHC),J,O,O,F,(vEC),(hH),O,O,(hB,vEC),O,O,X,(hEH),O,O,O,O,X,X,(hEA),D,O,X','6,X,X,(vAF),(vBF),X,X,X,(hBI),O,G,(vAD),(vBD),X,(hBI,vF),O,J,O,E,(hBB),A,G,(hBI,vBI),O,H,(hAJ),B,O,O,O,X,X,X,(hBA),O,O,X','6,X,(vCB),(vJ),X,X,X,(hCE),A,O,(vCI),X,X,(hCG),D,O,O,(vCC),X,X,(hCA),O,O,O,(vB),X,X,(hB),O,E,G,X,X,X,(hG),O,H','7,X,X,X,X,X,(vFI),(vHG),X,X,X,X,(hHJ,vHH),O,O,X,X,(vHC),(hHD,vHG),O,O,O,X,(hHH),O,O,O,O,X,X,(hFE,vHC),O,O,O,D,X,(hHE),H,O,O,X,X,X,(hHE),I,A,X,X,X,X','7,X,X,(vFA),(vC),X,X,X,X,(hE),O,B,(vAC),(vGJ),X,X,(hFF,vG),O,O,O,O,(vAI),(hAA),O,D,(hAB,vAC),O,O,O,(hAH),O,O,O,(hAB,vAB),O,O,X,(hFJ),O,O,O,O,X,X,X,X,(hAH),O,J,X','7,X,X,X,(vIF),(vIB),X,X,X,X,(hID),O,O,(vC),X,X,(vIF),(hIH,vEE),O,O,O,(vII),(hEB),O,O,O,(hIB,vIF),D,J,(hIF),O,O,(hII,vIE),O,O,O,X,(hJ),O,G,O,X,X,X,X,(hIF),O,O,X,X','7,X,(vDJ),(vDB),X,X,X,X,(hDJ),O,O,(vDF),(vCE),(vI),X,(hCH),O,O,O,O,O,X,X,X,(hDC,vDB),O,A,G,X,X,(hFE),O,O,O,(vDJ),(vI),X,(hCF),O,O,O,O,O,X,X,X,X,(hDE),O,O','6,X,X,(vCI),(vJ),X,X,X,(hA),O,E,(vEG),(vCC),X,(hEG,vCF),O,O,D,O,(hJ),C,G,(hB,vCC),C,O,(hED),O,O,A,O,X,X,X,(hCD),O,O,X','6,X,X,X,(vG),(vFE),X,X,X,(hG,vBC),O,O,(vBC),X,(hFJ,vC),O,E,O,I,(hG),O,O,(hBF,vBC),O,O,(hEJ),O,O,O,O,X,X,(hBA),D,O,X,X','6,X,X,(vAJ),(vE),X,X,X,(hFH,vH),O,O,(vFA),X,(hFH),O,O,O,O,(vFI),(hI),O,C,(hFI,vFD),O,O,X,(hAC),O,O,I,G,X,X,(hC),O,O,X','6,X,X,X,(vE),(vCJ),X,X,(vFF),(hA,vHJ),C,O,X,(hFC),O,O,O,F,(vD),(hFI),O,O,(hFE,vFJ),O,O,X,(hFG),O,O,O,O,X,(hFD),O,O,X,X','7,X,X,X,(vBJ),(vBI),X,X,X,X,(hA),O,O,(vCH),(vBJ),X,(vCJ),(hCB,vG),H,O,I,B,(hBA),O,O,O,(hBE,vG),O,O,(hBB),F,O,(hBE,vBI),O,O,O,(hBI),O,O,O,O,X,X,X,X,(hBC),O,O,X,X','6,X,X,(vCJ),(vD),X,X,X,(hH),O,O,(vBD),(vJ),X,(hCI,vCH),O,J,F,O,(hCG),O,E,(hA,vCD),O,F,(hBF),O,O,O,O,X,X,X,(hCG),O,O,X','6,X,X,X,X,(vJB),(vG),X,X,X,(hA,vH),I,O,X,X,(hCD,vCG),O,O,B,X,(hCF,vCD),O,O,O,X,(hJD),O,H,O,X,X,(hB),O,O,X,X,X','7,X,(vI),(vEH),X,X,(vCC),(vF),(hG),O,O,X,(hH),O,C,(hJ),O,O,(vAD),(hAG,vG),O,O,X,(hEI),F,O,O,O,X,X,(hAD,vAB),O,O,I,O,(vI),(hG),O,O,X,(hC),O,O,(hAJ),O,O,X,(hAA),O,O','7,X,X,X,X,X,(vEC),(vEA),X,X,X,X,(hB),O,O,X,X,(vDF),(vEH),(hEC,vH),H,O,X,(hEA,vI),O,B,E,O,O,(hDB),E,J,O,D,O,X,(hEH),O,A,X,X,X,X,(hI),O,O,X,X,X,X','6,X,X,X,(vBC),(vBC),X,X,X,(hBJ,vEC),H,O,(vBB),X,(hBE,vA),D,J,O,O,(hC),O,O,(hBE,vBG),O,O,(hEG),H,O,B,O,X,X,(hBI),O,O,X,X','7,X,(vE),(vCF),X,X,X,X,(hJ),O,O,(vFB),X,X,X,(hCJ),O,O,A,(vFE),(vCA),X,X,(hIH),O,O,O,O,X,X,(hFF),O,O,O,B,(vFA),X,X,X,(hCI),O,O,O,X,X,X,X,(hFG),O,O','7,X,X,X,X,(vBH),(vH),X,X,X,X,(hI),O,O,(vE),X,X,X,(hJG,vBF),O,O,O,X,(vH),(hBA,vJE),O,O,O,O,(hDG),O,O,O,O,X,X,(hBG),O,F,O,X,X,X,X,(hA),J,O,X,X,X','7,X,X,X,X,X,(vIC),(vA),X,X,X,(vII),(hG,vIH),F,I,X,X,(hIG),O,O,O,D,X,X,(hC,vC),O,O,J,X,X,(hIF,vE),O,G,A,X,X,(hIH),O,O,O,O,X,X,(hJ),F,D,X,X,X,X','7,X,X,X,(vH),(vCJ),X,X,X,(vCG),(hCB,vEG),O,O,X,X,(hEF),O,I,O,O,(vCI),X,(hCD),O,J,(hCB,vCJ),E,O,(vCC),X,(hCE),O,O,(hCI,vH),O,O,X,X,(hEB),O,O,O,O,X,X,(hD),O,O,X,X','6,X,(vGA),(vBE),X,X,X,(hGC),H,O,(vGF),X,X,(hGG),O,O,O,(vGD),X,X,(hBG),O,J,O,(vGD),X,X,(hGD),O,O,E,X,X,X,(hGH),O,O','6,X,X,(vEE),(vEJ),X,X,X,(hI,vEF),O,O,(vEH),X,(hEA),O,O,O,E,(vB),(hEE),O,O,(hB,vB),O,O,X,(hEG),A,O,I,O,X,X,(hA),D,B,X','6,X,(vJ),(vHA),X,X,X,(hHH),D,O,(vHG),X,X,(hI),O,O,F,(vDG),X,X,(hDJ),O,O,O,(vHF),X,X,(hHF),O,O,E,X,X,X,(hHE),B,O','6,X,X,X,X,(vFI),(vE),X,X,X,(hH,vA),J,I,X,X,(hGF,vD),O,O,F,X,(hGF,vC),O,O,A,X,(hD),O,O,O,X,X,(hD),O,O,X,X,X','7,X,X,(vHG),(vE),X,X,X,X,(hGD),O,O,(vGA),(vHC),(vAJ),X,(hGD,vAC),O,O,O,O,O,(hGC),O,O,(hAA,vGC),O,O,O,(hAC),O,O,F,(hGD,vD),O,O,(hHB),O,O,O,O,O,X,X,X,X,(hI),O,D,X','7,X,X,(vBG),(vBJ),X,(vBD),(vE),X,(hC),O,O,(hBB,vAG),O,C,X,(hBE),O,O,O,O,D,X,(hBG),O,O,O,(vBE),X,X,(vE),(hBI,vJ),O,O,O,X,(hCG),F,G,O,O,O,X,(hC),O,O,(hBJ),O,O,X','7,X,X,X,X,X,(vEA),(vJJ),X,X,(vED),(vJI),(hF),O,O,X,(hB),O,O,(hJH,vB),O,O,X,(hED),O,B,O,O,X,X,(hJI,vJI),O,O,C,O,X,(hJH),O,O,(hJJ),O,O,X,(hF),J,E,X,X,X,X','6,X,(vF),(vED),X,X,X,(hEI),O,O,(vEA),X,X,(hEJ),O,O,J,(vB),X,X,(hB),O,O,O,(vG),X,X,(hJ),B,O,C,X,X,X,(hF),O,E','6,X,X,X,X,(vCH),(vCD),X,X,X,(hG,vCH),O,O,X,X,(hCH,vCI),O,O,O,X,(hFA,vCE),O,O,J,X,(hFF),O,O,O,X,X,(hI),F,C,X,X,X','6,X,X,(vCH),(vA),X,X,X,(hE,vE),D,O,(vAG),(vHC),(hHB),O,O,C,O,I,(hHA),O,O,(hE,vJ),O,O,(hCH),A,O,O,O,O,X,X,(hHD),O,O,X','7,X,(vF),(vDG),(vGD),X,X,X,(hA),O,D,O,(vI),(vGE),X,(hDG),O,C,O,O,O,X,(hGC),H,O,(hH,vA),O,O,(vGF),X,(hH),O,O,(hGB,vGD),O,O,X,(hDH),O,D,O,O,O,X,X,X,(hA),O,O,G','7,X,X,X,X,(vIG),(vIG),X,X,X,X,(hCJ),O,O,(vCE),X,X,X,(hIE,vEA),O,O,O,X,(vJ),(hEA,vIE),O,O,O,O,(hCH),O,F,O,O,X,X,(hCH),I,B,O,X,X,X,X,(hCH),O,O,X,X,X','7,X,X,X,X,(vJ),(vDB),X,X,X,X,(hDG,vH),O,O,X,X,(vB),(hJ,vEB),E,O,O,(vG),(hDJ),O,F,D,(hI,vDC),O,O,(hA),O,O,(hJ,vA),O,O,I,X,(hDA),O,O,O,X,X,X,(hDH),O,O,X,X,X','6,X,X,X,(vEE),(vJA),(vEI),X,X,(hD,vEE),O,F,O,X,(hED,vEC),O,O,O,O,(hJ),O,O,(hEH,vEI),O,O,(hIB),O,O,O,O,X,(hII),O,O,O,X,X','6,X,(vE),(vGH),X,X,X,(hC),O,J,(vFJ),X,X,(hGH),O,O,O,(vJ),X,X,(hFA),B,O,I,(vFF),X,X,(hFG),O,O,O,X,X,X,(hB),F,G','6,X,X,(vIF),(vIJ),X,X,X,(hD,vIC),O,O,X,X,(hIB),O,O,O,(vIG),(vA),(hBF),O,O,F,I,O,X,X,(hE),D,O,F,X,X,(hIF),O,C,X','7,X,(vCD),(vB),X,X,X,X,(hII),O,D,(vA),X,X,X,(hIJ),O,O,O,(vII),X,X,(hID),O,O,O,O,(vIJ),(vCJ),X,X,(hCA),H,O,F,O,X,X,X,(hA),O,O,G,X,X,X,X,(hII),J,O','7,X,(vC),(vFF),X,X,(vHF),(vD),(hFD),O,O,(vHG),(hA,vFJ),O,O,(hHF),O,O,O,O,O,O,X,X,(hFG,vFH),O,O,O,X,X,(hFB,vI),O,O,O,(vFB),(vB),(hIG),O,O,O,O,D,J,(hG),O,I,X,(hFE),O,O','7,X,(vHJ),(vDE),X,X,(vDI),(vHH),(hHG),O,J,(vHJ),(hJ),O,O,(hHE),O,O,O,(hHJ,vB),O,O,X,(hHH),O,O,O,O,X,X,(hDJ,vHA),D,O,E,O,(vF),(hHJ),O,O,(hA),O,O,E,(hHA),O,O,X,(hI),O,O','7,X,(vEH),(vFA),X,X,X,X,(hEB),O,O,(vFA),X,X,X,(hFD),O,O,O,(vEE),(vID),X,X,(hFB),O,O,O,O,X,X,(hFJ),O,O,O,O,(vEE),X,X,X,(hJ),O,B,O,X,X,X,X,(hEH),C,O','6,X,(vJ),(vE),X,X,X,(hA),B,C,(vCJ),X,X,(hCG),O,O,O,(vCD),X,X,(hHF),O,O,O,(vJ),X,X,(hE),O,O,H,X,X,X,(hCE),O,O','6,X,(vGC),(vGH),X,X,X,(hGG),O,O,(vGB),X,X,(hGI),E,O,I,(vGG),X,X,(hIJ),O,C,O,(vA),X,X,(hD),G,O,O,X,X,X,(hD),O,O','6,X,X,X,X,(vIG),(vII),X,X,X,(hE,vIA),I,G,X,X,(hGJ,vGF),O,C,O,X,(hIE,vII),D,O,O,X,(hGJ),O,B,O,X,X,(hA),O,J,X,X,X','6,X,X,X,X,(vIA),(vE),X,X,(vJB),(hB,vII),I,J,X,(hIF),O,O,O,H,X,(hIB,vG),D,J,O,X,(hJG),C,O,O,F,X,(hB),O,O,X,X,X','7,X,X,X,(vDB),(vGG),X,X,X,X,(hGH),O,O,(vGA),(vGA),X,X,(hGF,vGA),O,O,O,O,X,(hGA,vGE),B,O,(hGD,vI),O,O,(hJ),O,I,(hGE,vGG),O,O,X,(hDA),O,D,O,O,X,X,X,X,(hF),O,O,X,X','6,X,X,X,(vFB),(vI),X,X,X,(hGF),O,O,(vGA),X,(vH),(hGA,vFD),O,O,O,(hFF),O,A,O,O,C,(hGG),O,J,O,X,X,X,(hGH),O,D,X,X','6,X,X,(vGA),(vA),X,X,X,(hB,vGE),O,O,(vHJ),X,(hBD),O,O,O,O,(vGH),(hGC),O,O,(hGJ,vGE),O,O,X,(hGG),O,F,O,O,X,X,(hGC),O,O,X','7,X,X,(vCE),(vG),(vI),X,X,X,(hEE),A,O,E,(vCD),(vCH),X,(hEG,vCD),O,O,O,O,O,(hA),G,C,X,(hEH),O,O,(hEE),O,O,(vI),(hA,vD),O,O,(hCF),O,O,O,O,O,X,X,X,(hED),O,O,B,X','7,X,(vG),(vDC),X,(vBA),(vDG),X,(hJ),O,G,(hDA,vBA),O,O,X,(hBC),O,O,G,O,O,X,X,(hDH),O,O,O,(vG),X,X,X,(hG,vDI),O,O,O,(vJ),X,(hBB),E,O,O,O,O,X,(hH),O,J,(hB),O,O','6,X,X,X,(vJG),(vCG),X,X,(vJG),(hJB,vJH),O,O,X,(hJH),I,B,O,O,(vD),(hJB),O,O,(hA,vJG),O,O,X,(hJB),O,B,O,O,X,(hF),I,C,X,X','7,X,(vA),(vE),X,X,(vD),(vB),(hF),O,O,(vJJ),(hI,vGD),O,O,(hGD),O,O,O,O,I,O,X,X,(hJI),O,O,X,X,X,(vJE),(hA,vF),I,O,(vD),(vJJ),(hGA),O,O,O,J,O,O,(hH),O,O,X,(hI),O,O','7,X,X,(vEH),(vEF),X,X,X,X,(hEI,vIH),O,O,(vEI),X,X,(hEI),O,O,O,O,(vIE),(vEJ),(hD),O,O,(hEH,vH),O,O,O,(hEC),O,O,O,(hD,vC),H,G,X,X,(hIA),O,O,O,O,X,X,X,(hD),E,O,X','7,X,X,X,X,X,(vEA),(vCJ),X,X,X,X,(hCD,vCC),O,O,X,X,(vCI),(hCJ,vEH),O,O,O,X,(hDH),O,J,B,O,X,X,(hCH,vD),O,O,O,O,X,(hCJ),O,O,O,X,X,X,(hJ),O,G,X,X,X,X','7,X,(vB),(vFF),X,(vEI),(vFE),X,(hH),O,O,(hFC,vIB),G,O,X,(hFC),O,O,O,O,O,X,X,X,(hFH),O,D,X,X,X,X,(hFF,vFG),O,O,(vFE),(vFH),X,(hEE),O,O,J,O,O,X,(hFG),O,O,(hFG),O,O','6,X,(vHE),(vII),X,X,X,(hHB),O,O,(vHF),(vHJ),X,(hHD),B,O,O,O,X,X,(hG),H,O,O,(vHE),X,(hCA),O,O,E,B,X,X,X,(hHB),O,G','6,X,(vH),(vAF),X,X,X,(hAC),O,O,(vAD),X,X,(hDI),J,O,O,(vAH),X,X,(hAC),O,O,O,(vAI),X,X,(hH),O,O,B,X,X,X,(hAH),O,E','6,X,(vC),(vHA),X,X,X,(hC),O,J,(vHA),X,X,(hF),J,O,O,(vHC),X,X,(hI),O,J,O,(vF),X,X,(hEJ),O,O,B,X,X,X,(hG),O,O','6,X,X,X,(vFJ),(vJC),X,X,(vFF),(hFF,vJE),O,O,X,(hFH),O,F,O,O,(vD),(hFI),O,C,(hE,vH),D,O,X,(hJC),O,O,O,A,X,(hFG),O,J,X,X','7,X,X,X,X,X,(vDE),(vBB),X,(vC),(vDF),X,(hBF),O,O,(hH),O,O,(vE),(hH,vBI),B,O,(hDF),O,O,O,O,D,(vE),X,(hDI,vBE),O,O,C,O,B,(hBF),O,A,X,(hG),E,D,(hG),O,O,X,X,X,X','7,X,(vJ),(vFH),X,X,X,X,(hHH),F,A,X,X,(vGE),(vA),(hI),O,O,(vC),(hF,vD),O,O,X,(hHC,vF),H,O,O,O,O,(hGJ),O,O,O,O,O,(vE),(hE),O,O,X,(hHI),O,O,X,X,X,X,(hA),O,O','7,X,X,(vCD),(vCB),(vF),X,X,X,(hCA,vCJ),O,O,O,(vFH),X,(hCD),O,O,O,O,O,(vCB),(hH),O,O,X,(hI),O,O,(hCE),O,B,(vCE),(hCH,vCI),O,G,X,(hFA),O,G,O,O,O,X,X,(hBC),H,O,O,X','6,X,X,X,X,(vHD),(vHH),X,X,X,(hA,vHH),H,I,X,X,(hHJ,vIG),O,C,O,X,(hHC,vE),O,O,O,X,(hIG),J,O,O,X,X,(hHF),O,O,X,X,X','6,X,X,(vFD),(vJB),X,X,X,(hH,vH),O,O,(vJD),X,(hFH),O,O,O,O,(vJI),(hJD),O,O,(hJD,vG),J,E,X,(hJD),O,O,O,O,X,X,(hB),A,O,X','6,X,X,X,(vC),(vDC),X,X,(vF),(hHB,vDI),O,O,(vDJ),(hDG),O,O,E,O,O,(hHA),O,O,(hHD,vG),O,O,(hEJ),O,O,F,O,O,X,(hJ),O,O,X,X','7,X,X,X,X,X,(vEJ),(vG),X,X,X,X,(hD,vI),C,O,X,X,(vEG),(hFE,vFE),O,O,O,X,(hFD),O,O,O,O,X,X,(hEC,vFI),O,O,O,O,X,(hEC),B,O,H,X,X,X,(hJ),O,O,X,X,X,X','7,X,(vI),(vAC),X,X,(vAI),(vCG),(hB),O,I,X,(hCB,vCD),O,O,(hH),A,D,(hCD,vAF),O,O,O,X,(hAC),O,O,O,O,X,X,(hCF,vCC),O,O,O,O,(vB),(hCB),O,O,O,(hCF),O,O,(hCB),O,J,X,(hB),O,O','6,X,X,X,(vJB),(vIG),X,X,(vA),(hJI,vJC),O,F,X,(hJB),O,O,O,O,(vJE),(hJD),B,O,(hJB,vD),O,H,X,(hJG),O,I,O,O,X,(hA),O,E,X,X','7,X,X,X,X,(vCD),(vCC),(vB),X,X,X,(hCC,vEC),O,I,O,X,X,(hCH),C,O,O,O,X,X,(hCA),F,O,X,X,X,(vA),(hCH,vCE),O,E,X,X,(hGA),C,O,O,O,X,X,(hCE),O,O,O,X,X,X','6,X,X,X,X,(vJI),(vA),X,X,(vJH),(hJE,vJI),O,G,X,(hJE),F,O,O,D,X,(hC,vB),O,E,O,X,(hJH),O,O,O,O,X,(hJD),O,E,X,X,X','6,X,X,X,X,(vAJ),(vAJ),X,X,X,(hAF,vGB),O,O,X,X,(hAE,vD),O,O,O,X,(hAJ,vF),O,J,O,X,(hAF),O,O,H,X,X,(hB),O,I,X,X,X','7,X,X,X,X,(vH),(vIE),X,X,X,X,(hA,vA),O,O,X,X,(vID),(hF,vCH),O,O,A,(vIE),(hIH),O,O,O,(hIA,vIH),O,O,(hIE),O,O,(hIG,vIA),B,O,O,X,(hIF),O,G,A,X,X,X,(hIE),O,D,X,X,X','7,X,(vEF),(vB),(vFC),X,X,X,(hH),O,O,O,(vEA),X,X,(hED),C,O,O,O,X,X,X,X,(hEG),O,F,X,X,X,X,(hEI),O,O,(vEH),(vI),X,X,(hFH),O,O,O,O,X,X,X,(hEE),O,I,O','6,X,(vHI),(vDG),X,X,X,(hHE),J,O,(vDG),X,X,(hHC),H,O,O,(vHA),X,X,(hDH),F,O,G,(vHE),X,X,(hHC),O,O,O,X,X,X,(hHE),O,O','6,X,X,(vAD),(vAE),X,X,X,(hAA),O,O,(vAD),(vAA),X,(hAI,vI),O,F,D,J,(hC),A,O,(hB,vJ),A,E,(hAB),O,I,C,J,X,X,X,(hI),O,H,X','6,X,X,(vDA),(vE),X,X,X,(hJ,vDE),O,F,(vGG),X,(hDJ),O,O,O,O,(vC),(hDD),O,O,(hJ,vI),O,O,X,(hGG),O,D,O,O,X,X,(hDA),G,B,X','7,X,X,(vJD),(vG),(vI),X,X,X,(hG),O,O,H,(vEB),(vEF),X,(hEB),O,O,B,O,J,X,(hEJ,vA),O,H,(hEE,vEA),O,O,(hA),O,O,(hEJ,vG),O,O,X,(hJF),O,O,O,O,O,X,X,X,(hG),F,O,O,X','6,X,X,X,X,(vEJ),(vG),X,X,X,(hDE,vF),O,O,X,X,(hDJ,vF),O,O,O,X,(hA,vDA),O,O,O,X,(hDI),B,O,O,X,X,(hDE),C,O,X,X,X','6,X,X,(vAC),(vD),X,X,X,(hD,vEI),O,O,(vBC),X,(hBA),O,O,O,O,(vH),(hEF),O,O,(hEI,vF),O,O,X,(hEF),O,O,A,O,X,X,(hEE),G,D,X','6,X,X,(vGB),(vD),X,X,X,(hGG),A,C,(vGJ),(vC),X,(hGG,vGC),O,O,O,J,(hGH),O,O,(hE,vI),G,H,(hHF),O,H,O,O,X,X,X,(hE),O,O,X','6,X,X,(vIJ),(vCD),X,X,X,(hCD),O,O,(vCI),(vCG),X,(hIH,vCC),G,O,O,O,(hCE),O,I,(hCH,vCD),G,O,(hIC),B,D,O,O,X,X,X,(hA),O,O,X','7,X,(vII),(vDH),(vID),X,X,X,(hIG),O,O,O,X,X,X,(hDA),O,C,J,(vII),X,X,X,(hID),F,O,O,(vDH),X,X,X,(hID),O,O,O,(vID),X,X,X,(hIE),A,O,O,X,X,X,(hDD),O,O,O','7,X,(vEB),(vF),X,X,X,X,(hED),O,O,(vAJ),(vED),(vD),X,(hIB),O,O,O,G,O,X,X,X,(hF,vA),O,O,O,X,X,(hED),O,O,F,(vA),(vEB),X,(hIE),O,H,O,O,O,X,X,X,X,(hEE),O,O','7,X,X,X,X,(vCA),(vCE),(vB),X,X,X,(hF),O,O,O,X,X,X,(hJG,vCD),I,O,O,X,X,(hF,vB),O,O,O,X,X,(hJI,vCI),O,F,O,X,X,(hD),O,O,O,X,X,X,(hCI),O,O,O,X,X,X','6,X,(vJI),(vI),X,X,X,(hH),O,O,(vD),X,X,(hJA),F,O,O,(vJH),X,X,(hJI),C,G,O,(vJJ),X,X,(hD),O,O,O,X,X,X,(hJE),O,O','6,X,X,X,(vDC),(vAE),X,X,X,(hI),O,B,(vI),X,(vC),(hJ,vDE),O,O,O,(hAF),A,D,O,O,O,(hI),O,O,G,X,X,X,(hDA),H,O,X,X','7,X,X,X,(vFD),(vAF),X,X,X,(vFD),(hFE,vFA),B,O,X,X,(hHI),O,O,O,O,(vFF),X,(hFI),O,O,(hC,vG),O,H,(vFA),X,(hE),O,O,(hFB,vC),O,O,X,X,(hFJ),O,G,O,O,X,X,(hH),O,O,X,X','7,X,X,X,X,(vD),(vHD),X,X,X,(vDH),(hA,vJJ),O,O,(vE),X,(hHB,vJH),O,O,O,E,J,(hJE),H,O,O,(hD,vF),O,O,(hJG),E,O,(hJE,vJG),C,O,O,(hHH),J,O,O,O,O,X,X,(hJJ),O,O,X,X,X','7,X,X,X,X,(vBA),(vEB),X,X,X,(vBG),(hC,vBB),O,O,X,X,(hBD,vBA),O,O,O,O,(vBJ),(hBC),O,O,O,(hBG,vBD),A,O,(hBB),O,O,(hEE,vBF),O,O,D,X,(hBJ),O,O,O,I,X,X,(hBD),O,O,X,X,X','7,X,X,X,X,X,(vDG),(vC),X,(vB),(vFH),X,(hC),E,O,(hA),O,O,(vDD),(hH,vDB),O,O,(hDA),C,O,O,O,O,(vE),X,(hFH,vDE),O,O,H,O,F,(hDH),O,O,X,(hDI),O,O,(hJ),O,O,X,X,X,X','6,X,(vB),(vE),X,X,X,(hA),D,O,(vA),X,X,(hH),O,C,O,(vIG),X,X,(hDI),O,O,O,(vDF),X,X,(hIF),O,O,O,X,X,X,(hH),O,O','7,X,(vHF),(vC),X,X,(vC),(vHF),(hC),O,O,(vBC),(hA,vBF),O,O,(hBE),O,O,O,O,O,O,X,X,(hHD),A,O,X,X,X,(vD),(hJ,vHA),O,O,(vHI),(vC),(hCH),J,O,O,O,O,B,(hHH),O,O,X,(hE),O,O','6,X,X,X,(vJ),(vDA),X,X,(vFD),(hB,vFE),O,O,(vDA),(hDJ),O,O,O,O,O,(hDE),O,O,(hDA,vC),O,H,(hBA),O,I,O,G,O,X,(hJ),E,O,X,X','6,X,(vGA),(vA),X,X,X,(hGE),O,O,(vGD),X,X,(hGA),O,G,A,(vED),X,X,(hGE),O,O,O,(vGD),X,X,(hEB),C,H,F,X,X,X,(hGE),A,I','6,X,(vIC),(vFD),X,X,X,(hIG),O,C,(vIB),X,X,(hFJ),O,O,O,(vII),X,X,(hIE),O,O,F,(vIA),X,X,(hIJ),F,I,O,X,X,X,(hIC),O,O','6,X,X,X,(vJG),(vHH),X,X,X,(hHA),O,O,(vHD),X,(vE),(hJF,vHJ),O,O,O,(hHB),F,O,D,O,O,(hE),O,J,O,X,X,X,(hHE),I,O,X,X','7,X,X,X,(vGG),(vI),(vEC),X,X,(vBH),(hJ,vBI),O,O,O,X,(hBJ),O,O,O,O,O,(vJ),(hGJ),O,O,X,(hA),O,O,(hGC),O,O,(vC),(hGB,vGJ),O,O,X,(hBF),O,O,O,O,B,X,(hBH),O,O,O,X,X','7,X,X,X,X,X,(vD),(vHB),X,X,(vG),(vFC),(hHA,vAI),O,O,X,(hAB),O,O,O,O,O,X,(hAD),O,O,O,(vHB),X,X,(vF),(hAF,vHI),O,O,O,X,(hAB),O,O,O,O,O,X,(hB),O,E,X,X,X,X','6,X,(vBC),(vDF),X,X,X,(hBE),O,O,(vDB),X,X,(hDG),O,J,O,(vC),X,X,(hBI),O,O,O,(vBB),X,X,(hBA),O,O,D,X,X,X,(hBG),F,O','6,X,X,X,(vH),(vDC),(vGA),X,X,(hA,vIE),O,O,O,X,(hIG,vGG),O,O,O,O,(hF),O,O,(hGF,vJ),J,O,(hGA),O,O,O,O,X,(hIE),O,O,O,X,X','6,X,(vHC),(vHJ),X,X,X,(hHC),A,B,(vA),X,X,(hHI),O,O,O,(vHA),X,X,(hD),F,O,O,(vB),X,X,(hII),G,O,O,X,X,X,(hB),O,O','7,X,(vH),(vJA),X,X,(vIE),(vJI),(hJC),O,O,(vDG),(hJE,vIG),O,O,(hDD),I,O,O,O,O,O,X,X,(hII,vIG),O,O,O,X,X,(hIE,vJA),O,O,O,(vB),(vJI),(hDG),C,O,O,O,O,O,(hJF),O,O,X,(hH),O,O','7,X,(vHH),(vBE),X,X,X,X,(hE),B,O,X,(vHF),(vBJ),X,(hHI),C,O,(hJ,vHI),O,O,X,X,(hBC),D,O,O,O,X,X,(hHH),O,O,D,O,(vHF),X,(hHD),F,O,(hHD),G,O,X,X,X,X,(hHE),O,O','7,X,X,X,X,X,(vIF),(vI),X,X,X,X,(hB,vGF),O,O,X,X,(vEG),(hGG,vB),O,O,O,X,(hGJ),O,O,O,H,X,X,(hGA,vA),O,O,O,O,X,(hGC),I,H,O,X,X,X,(hH),G,J,X,X,X,X','7,X,X,X,X,X,(vJF),(vJF),X,X,X,X,(hJD),A,O,X,X,(vBG),(vJB),(hI,vI),O,O,X,(hBD,vJF),F,O,O,E,O,(hIB),O,O,O,O,C,X,(hJG),O,B,X,X,X,X,(hI),O,J,X,X,X,X','6,X,X,(vEI),(vC),X,X,X,(hH,vGG),O,O,(vGD),X,(hBJ),O,O,O,O,(vD),(hGI),O,O,(hD,vD),E,G,X,(hBG),O,O,A,O,X,X,(hJ),O,O,X','7,X,X,X,X,(vFI),(vJF),X,X,X,X,(hJH),O,O,(vJC),X,X,X,(hEE,vEC),O,O,O,X,(vJE),(hED,vEF),O,O,O,G,(hJB),O,O,O,O,X,X,(hEH),O,O,G,X,X,X,X,(hJG),O,O,X,X,X','7,X,X,X,(vJ),(vEI),X,X,X,X,(hJ,vEC),O,A,(vBD),X,X,(hHC,vEA),O,O,O,I,(vF),(hEE),O,O,(hEE,vHD),B,J,O,(hHE),O,O,O,(hG,vED),O,O,X,(hHD),O,O,O,O,X,X,X,(hEA),O,O,X,X','7,X,X,X,X,X,(vFH),(vED),X,X,X,X,(hEC,vEA),O,O,X,X,(vED),(hFI,vEH),O,O,O,X,(hEE),O,O,A,D,X,X,(hFB,vJ),O,O,O,J,X,(hFI),O,O,O,X,X,X,(hI),O,A,X,X,X,X','6,X,(vB),(vHI),X,X,X,(hHH),O,O,(vHJ),(vGA),X,(hHH),O,O,O,I,X,X,(hGE),O,A,O,(vHE),X,(hHJ),H,B,F,D,X,X,X,(hHJ),O,C'
+]
+
+kakuro(testPuzzles);
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-425-prime-connection.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-425-prime-connection.md
new file mode 100644
index 00000000000..dfba791e407
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-425-prime-connection.md
@@ -0,0 +1,53 @@
+---
+id: 5900f5151000cf542c510028
+title: 'Problem 425: Prime connection'
+challengeType: 1
+forumTopicId: 302095
+dashedName: problem-425-prime-connection
+---
+
+# --description--
+
+Two positive numbers $A$ and $B$ are said to be connected (denoted by "$A ↔ B$") if one of these conditions holds:
+
+1. $A$ and $B$ have the same length and differ in exactly one digit; for example, $123 ↔ 173$.
+2. Adding one digit to the left of $A$ (or $B$) makes $B$ (or $A$); for example, $23 ↔ 223$ and $123 ↔ 23$.
+
+We call a prime $P$ a 2's relative if there exists a chain of connected primes between 2 and $P$ and no prime in the chain exceeds $P$.
+
+For example, 127 is a 2's relative. One of the possible chains is shown below:
+
+$$2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127$$
+
+However, 11 and 103 are not 2's relatives.
+
+Let $F(N)$ be the sum of the primes $≤ N$ which are not 2's relatives. We can verify that $F({10}^3) = 431$ and $F({10}^4) = 78\\,728$.
+
+Find $F({10}^7)$.
+
+# --hints--
+
+`primeConnection()` should return `46479497324`.
+
+```js
+assert.strictEqual(primeConnection(), 46479497324);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function primeConnection() {
+
+ return true;
+}
+
+primeConnection();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-426-box-ball-system.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-426-box-ball-system.md
new file mode 100644
index 00000000000..89314f8aa76
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-426-box-ball-system.md
@@ -0,0 +1,61 @@
+---
+id: 5900f5171000cf542c510029
+title: 'Problem 426: Box-ball system'
+challengeType: 1
+forumTopicId: 302096
+dashedName: problem-426-box-ball-system
+---
+
+# --description--
+
+Consider an infinite row of boxes. Some of the boxes contain a ball. For example, an initial configuration of 2 consecutive occupied boxes followed by 2 empty boxes, 2 occupied boxes, 1 empty box, and 2 occupied boxes can be denoted by the sequence (2, 2, 2, 1, 2), in which the number of consecutive occupied and empty boxes appear alternately.
+
+A turn consists of moving each ball exactly once according to the following rule: Transfer the leftmost ball which has not been moved to the nearest empty box to its right.
+
+After one turn the sequence (2, 2, 2, 1, 2) becomes (2, 2, 1, 2, 3) as can be seen below; note that we begin the new sequence starting at the first occupied box.
+
+
+
+A system like this is called a Box-Ball System or BBS for short.
+
+It can be shown that after a sufficient number of turns, the system evolves to a state where the consecutive numbers of occupied boxes is invariant. In the example below, the consecutive numbers of occupied boxes evolves to [1, 2, 3]; we shall call this the final state.
+
+![four turns from occupied boxes [2, 2, 2] to final state [1, 2, 3]](https://cdn.freecodecamp.org/curriculum/project-euler/box-ball-system-2.gif)
+
+We define the sequence $\\{t_i\\}$:
+
+$$\begin{align} & s_0 = 290\\,797 \\\\
+ & s_{k + 1} = {s_k}^2\bmod 50\\,515\\,093 \\\\ & t_k = (s_k\bmod 64) + 1 \end{align}$$
+
+Starting from the initial configuration $(t_0, t_1, \ldots, t_{10})$, the final state becomes [1, 3, 10, 24, 51, 75].
+
+Starting from the initial configuration $(t_0, t_1, \ldots, t_{10\\,000\\,000})$, find the final state.
+
+Give as your answer the sum of the squares of the elements of the final state. For example, if the final state is [1, 2, 3] then $14 (= 1^2 + 2^2 + 3^2)$ is your answer.
+
+# --hints--
+
+`boxBallSystem()` should return `31591886008`.
+
+```js
+assert.strictEqual(boxBallSystem(), 31591886008);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function boxBallSystem() {
+
+ return true;
+}
+
+boxBallSystem();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-427-n-sequences.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-427-n-sequences.md
new file mode 100644
index 00000000000..3f244f7937c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-427-n-sequences.md
@@ -0,0 +1,48 @@
+---
+id: 5900f5181000cf542c51002a
+title: 'Problem 427: n-sequences'
+challengeType: 1
+forumTopicId: 302097
+dashedName: problem-427-n-sequences
+---
+
+# --description--
+
+A sequence of integers $S = \\{s_i\\}$ is called an $n$-sequence if it has $n$ elements and each element $s_i$ satisfies $1 ≤ s_i ≤ n$. Thus there are $n^n$ distinct $n$-sequences in total.
+
+For example, the sequence $S = \\{1, 5, 5, 10, 7, 7, 7, 2, 3, 7\\}$ is a 10-sequence.
+
+For any sequence $S$, let $L(S)$ be the length of the longest contiguous subsequence of $S$ with the same value. For example, for the given sequence $S$ above, $L(S) = 3$, because of the three consecutive 7's.
+
+Let $f(n) = \sum L(S)$ for all $n$-sequences $S$.
+
+For example, $f(3) = 45$, $f(7) = 1\\,403\\,689$ and $f(11) = 481\\,496\\,895\\,121$.
+
+Find $f(7\\,500\\,000)\bmod 1\\,000\\,000\\,009$.
+
+# --hints--
+
+`nSequences()` should return `97138867`.
+
+```js
+assert.strictEqual(nSequences(), 97138867);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function nSequences() {
+
+ return true;
+}
+
+nSequences();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-428-necklace-of-circles.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-428-necklace-of-circles.md
new file mode 100644
index 00000000000..bf6e6bdaa12
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-428-necklace-of-circles.md
@@ -0,0 +1,59 @@
+---
+id: 5900f5191000cf542c51002b
+title: 'Problem 428: Necklace of Circles'
+challengeType: 1
+forumTopicId: 302098
+dashedName: problem-428-necklace-of-circles
+---
+
+# --description--
+
+Let $a$, $b$ and $c$ be positive numbers.
+
+Let $W$, $X$, $Y$, $Z$ be four collinear points where $|WX| = a$, $|XY| = b$, $|YZ| = c$ and $|WZ| = a + b + c$.
+
+Let $C_{\text{in}}$ be the circle having the diameter $XY$.
+
+Let $C_{\text{out}}$ be the circle having the diameter $WZ$.
+
+The triplet ($a$, $b$, $c$) is called a *necklace triplet* if you can place $k ≥ 3$ distinct circles $C_1, C_2, \ldots, C_k$ such that:
+
+- $C_i$ has no common interior points with any $C_j$ for $1 ≤ i$, $j ≤ k$ and $i ≠ j$,
+- $C_i$ is tangent to both $C_{\text{in}}$ and $C_{\text{out}}$ for $1 ≤ i ≤ k$,
+- $C_i$ is tangent to $C_{i + 1}$ for $1 ≤ i < k$, and
+- $C_k$ is tangent to $C_1$.
+
+For example, (5, 5, 5) and (4, 3, 21) are necklace triplets, while it can be shown that (2, 2, 5) is not.
+
+
+
+Let $T(n)$ be the number of necklace triplets $(a, b, c)$ such that $a$, $b$ and $c$ are positive integers, and $b ≤ n$. For example, $T(1) = 9$, $T(20) = 732$ and $T(3\\,000) = 438\\,106$.
+
+Find $T(1\\,000\\,000\\,000)$.
+
+# --hints--
+
+`necklace(1000000000)` should return `747215561862`.
+
+```js
+assert.strictEqual(necklace(1000000000), 747215561862);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function necklace(n) {
+
+ return true;
+}
+
+necklace(1000000000)
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-429-sum-of-squares-of-unitary-divisors.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-429-sum-of-squares-of-unitary-divisors.md
new file mode 100644
index 00000000000..928c602299f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-429-sum-of-squares-of-unitary-divisors.md
@@ -0,0 +1,46 @@
+---
+id: 5900f5191000cf542c51002c
+title: 'Problem 429: Sum of squares of unitary divisors'
+challengeType: 1
+forumTopicId: 302099
+dashedName: problem-429-sum-of-squares-of-unitary-divisors
+---
+
+# --description--
+
+A unitary divisor $d$ of a number $n$ is a divisor of $n$ that has the property $gcd(d, \frac{n}{d}) = 1$.
+
+The unitary divisors of $4! = 24$ are 1, 3, 8 and 24.
+
+The sum of their squares is $12 + 32 + 82 + 242 = 650$.
+
+Let $S(n)$ represent the sum of the squares of the unitary divisors of $n$. Thus $S(4!) = 650$.
+
+Find $S(100\\,000\\,000!)$ modulo $1\\,000\\,000\\,009$.
+
+# --hints--
+
+`sumSquaresOfUnitaryDivisors()` should return `98792821`.
+
+```js
+assert.strictEqual(sumSquaresOfUnitaryDivisors(), 98792821);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumSquaresOfUnitaryDivisors() {
+
+ return true;
+}
+
+sumSquaresOfUnitaryDivisors();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-430-range-flips.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-430-range-flips.md
new file mode 100644
index 00000000000..d8838dbe162
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-430-range-flips.md
@@ -0,0 +1,50 @@
+---
+id: 5900f51a1000cf542c51002d
+title: 'Problem 430: Range flips'
+challengeType: 1
+forumTopicId: 302101
+dashedName: problem-430-range-flips
+---
+
+# --description--
+
+$N$ disks are placed in a row, indexed 1 to $N$ from left to right.
+
+Each disk has a black side and white side. Initially all disks show their white side.
+
+At each turn, two, not necessarily distinct, integers $A$ and $B$ between 1 and $N$ (inclusive) are chosen uniformly at random. All disks with an index from $A$ to $B$ (inclusive) are flipped.
+
+The following example shows the case $N = 8$. At the first turn $A = 5$ and $B = 2$, and at the second turn $A = 4$ and $B = 6$.
+
+
+
+Let $E(N, M)$ be the expected number of disks that show their white side after $M$ turns. We can verify that $E(3, 1) = \frac{10}{9}$, $E(3, 2) = \frac{5}{3}$, $E(10, 4) ≈ 5.157$ and $E(100, 10) ≈ 51.893$.
+
+Find $E({10}^{10}, 4000)$. Give your answer rounded to 2 decimal places behind the decimal point.
+
+# --hints--
+
+`rangeFlips()` should return `5000624921.38`.
+
+```js
+assert.strictEqual(rangeFlips(), 5000624921.38);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function rangeFlips() {
+
+ return true;
+}
+
+rangeFlips();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-431-square-space-silo.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-431-square-space-silo.md
new file mode 100644
index 00000000000..4199819468b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-431-square-space-silo.md
@@ -0,0 +1,48 @@
+---
+id: 5900f51b1000cf542c51002e
+title: 'Problem 431: Square Space Silo'
+challengeType: 1
+forumTopicId: 302102
+dashedName: problem-431-square-space-silo
+---
+
+# --description--
+
+Fred the farmer arranges to have a new storage silo installed on his farm and having an obsession for all things square he is absolutely devastated when he discovers that it is circular. Quentin, the representative from the company that installed the silo, explains that they only manufacture cylindrical silos, but he points out that it is resting on a square base. Fred is not amused and insists that it is removed from his property.
+
+Quick thinking Quentin explains that when granular materials are delivered from above a conical slope is formed and the natural angle made with the horizontal is called the angle of repose. For example if the angle of repose, $\alpha = 30°$, and grain is delivered at the centre of the silo then a perfect cone will form towards the top of the cylinder. In the case of this silo, which has a diameter of 6m, the amount of space wasted would be approximately 32.648388556 m3. However, if grain is delivered at a point on the top which has a horizontal distance of $x$ metres from the centre then a cone with a strangely curved and sloping base is formed. He shows Fred a picture.
+
+
+
+We shall let the amount of space wasted in cubic metres be given by $V(x)$. If $x = 1.114\\,785\\,284$, which happens to have three squared decimal places, then the amount of space wasted, $V(1.114\\,785\\,284) \approx 36$. Given the range of possible solutions to this problem there is exactly one other option: $V(2.511\\,167\\,869) \approx 49$. It would be like knowing that the square is king of the silo, sitting in splendid glory on top of your grain.
+
+Fred's eyes light up with delight at this elegant resolution, but on closer inspection of Quentin's drawings and calculations his happiness turns to despondency once more. Fred points out to Quentin that it's the radius of the silo that is 6 metres, not the diameter, and the angle of repose for his grain is 40°. However, if Quentin can find a set of solutions for this particular silo then he will be more than happy to keep it.
+
+If Quick thinking Quentin is to satisfy frustratingly fussy Fred the farmer's appetite for all things square then determine the values of $x$ for all possible square space wastage options and calculate $\sum x$ correct to 9 decimal places.
+
+# --hints--
+
+`squareSpaceSilo()` should return `23.386029052`.
+
+```js
+assert.strictEqual(squareSpaceSilo(), 23.386029052);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function squareSpaceSilo() {
+
+ return true;
+}
+
+squareSpaceSilo();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-432-totient-sum.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-432-totient-sum.md
new file mode 100644
index 00000000000..2a3f5b744d9
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-432-totient-sum.md
@@ -0,0 +1,42 @@
+---
+id: 5900f51e1000cf542c510030
+title: 'Problem 432: Totient sum'
+challengeType: 1
+forumTopicId: 302103
+dashedName: problem-432-totient-sum
+---
+
+# --description--
+
+Let $S(n, m) = \sum φ(n × i)$ for $1 ≤ i ≤ m$. ($φ$ is Euler's totient function)
+
+You are given that $S(510\\,510, {10}^6) = 45\\,480\\,596\\,821\\,125\\,120$.
+
+Find $S(510\\,510, {10}^{11})$. Give the last 9 digits of your answer.
+
+# --hints--
+
+`totientSum()` should return `754862080`.
+
+```js
+assert.strictEqual(totientSum(), 754862080);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function totientSum() {
+
+ return true;
+}
+
+totientSum();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-433-steps-in-euclids-algorithm.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-433-steps-in-euclids-algorithm.md
new file mode 100644
index 00000000000..4db4c121e91
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-433-steps-in-euclids-algorithm.md
@@ -0,0 +1,51 @@
+---
+id: 5900f51d1000cf542c51002f
+title: 'Problem 433: Steps in Euclid''s algorithm'
+challengeType: 1
+forumTopicId: 302104
+dashedName: problem-433-steps-in-euclids-algorithm
+---
+
+# --description--
+
+Let $E(x_0, y_0)$ be the number of steps it takes to determine the greatest common divisor of $x_0$ and $y_0$ with Euclid's algorithm. More formally:
+
+$$\begin{align} & x_1 = y_0, y_1 = x_0\bmod y_0 \\\\
+ & x_n = y_{n - 1}, y_n = x_{n - 1}\bmod y_{n - 1} \end{align}$$
+
+$E(x_0, y_0)$ is the smallest $n$ such that $y_n = 0$.
+
+We have $E(1, 1) = 1$, $E(10, 6) = 3$ and $E(6, 10) = 4$.
+
+Define $S(N)$ as the sum of $E(x, y)$ for $1 ≤ x$, $y ≤ N$.
+
+We have $S(1) = 1$, $S(10) = 221$ and $S(100) = 39\\,826$.
+
+Find $S(5 \times {10}^6)$.
+
+# --hints--
+
+`stepsInEuclidsAlgorithm()` should return `326624372659664`.
+
+```js
+assert.strictEqual(stepsInEuclidsAlgorithm(), 326624372659664);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function stepsInEuclidsAlgorithm() {
+
+ return true;
+}
+
+stepsInEuclidsAlgorithm();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-434-rigid-graphs.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-434-rigid-graphs.md
new file mode 100644
index 00000000000..a570e51bccb
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-434-rigid-graphs.md
@@ -0,0 +1,66 @@
+---
+id: 5900f51f1000cf542c510031
+title: 'Problem 434: Rigid graphs'
+challengeType: 1
+forumTopicId: 302105
+dashedName: problem-434-rigid-graphs
+---
+
+# --description--
+
+Recall that a graph is a collection of vertices and edges connecting the vertices, and that two vertices connected by an edge are called adjacent.
+
+Graphs can be embedded in Euclidean space by associating each vertex with a point in the Euclidean space.
+
+A flexible graph is an embedding of a graph where it is possible to move one or more vertices continuously so that the distance between at least two nonadjacent vertices is altered while the distances between each pair of adjacent vertices is kept constant.
+
+A rigid graph is an embedding of a graph which is not flexible.
+
+Informally, a graph is rigid if by replacing the vertices with fully rotating hinges and the edges with rods that are unbending and inelastic, no parts of the graph can be moved independently from the rest of the graph.
+
+The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates:
+
+
+
+However, one can make them rigid by adding diagonal edges to the cells. For example, for the 2x3 grid graph, there are 19 ways to make the graph rigid:
+
+
+
+Note that for the purposes of this problem, we do not consider changing the orientation of a diagonal edge or adding both diagonal edges to a cell as a different way of making a grid graph rigid.
+
+Let $R(m, n)$ be the number of ways to make the $m × n$ grid graph rigid.
+
+E.g. $R(2, 3) = 19$ and $R(5, 5) = 23\\,679\\,901$.
+
+Define $S(N)$ as $\sum R(i, j)$ for $1 ≤ i$, $j ≤ N$.
+
+E.g. $S(5) = 25\\,021\\,721$.
+
+Find $S(100)$, give your answer modulo $1\\,000\\,000\\,033$.
+
+# --hints--
+
+`rigidGraphs()` should return `863253606`.
+
+```js
+assert.strictEqual(rigidGraphs(), 863253606);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function rigidGraphs() {
+
+ return true;
+}
+
+rigidGraphs();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-435-polynomials-of-fibonacci-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-435-polynomials-of-fibonacci-numbers.md
new file mode 100644
index 00000000000..9df767adcee
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-435-polynomials-of-fibonacci-numbers.md
@@ -0,0 +1,44 @@
+---
+id: 5900f5201000cf542c510032
+title: 'Problem 435: Polynomials of Fibonacci numbers'
+challengeType: 1
+forumTopicId: 302106
+dashedName: problem-435-polynomials-of-fibonacci-numbers
+---
+
+# --description--
+
+The Fibonacci numbers $\\{f_n, n ≥ 0\\}$ are defined recursively as $f_n = f_{n - 1} + f_{n - 2}$ with base cases $f_0 = 0$ and $f_1 = 1$.
+
+Define the polynomials $\\{F_n, n ≥ 0\\}$ as $F_n(x) = \displaystyle\sum_{i = 0}^n f_ix^i$.
+
+For example, $F_7(x) = x + x^2 + 2x^3 + 3x^4 + 5x^5 + 8x^6 + 13x^7$, and $F_7(11) = 268\\,357\\,683$.
+
+Let $n = {10}^{15}$. Find the sum $\displaystyle\sum_{x = 0}^{100} F_n(x)$ and give your answer modulo $1\\,307\\,674\\,368\\,000 \\, (= 15!)$.
+
+# --hints--
+
+`polynomialsOfFibonacciNumbers()` should return `252541322550`.
+
+```js
+assert.strictEqual(polynomialsOfFibonacciNumbers(), 252541322550);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function polynomialsOfFibonacciNumbers() {
+
+ return true;
+}
+
+polynomialsOfFibonacciNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-436-unfair-wager.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-436-unfair-wager.md
new file mode 100644
index 00000000000..444c6f95d1b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-436-unfair-wager.md
@@ -0,0 +1,56 @@
+---
+id: 5900f5221000cf542c510033
+title: 'Problem 436: Unfair wager'
+challengeType: 1
+forumTopicId: 302107
+dashedName: problem-436-unfair-wager
+---
+
+# --description--
+
+Julie proposes the following wager to her sister Louise.
+
+She suggests they play a game of chance to determine who will wash the dishes.
+
+For this game, they shall use a generator of independent random numbers uniformly distributed between 0 and 1.
+
+The game starts with $S = 0$.
+
+The first player, Louise, adds to $S$ different random numbers from the generator until $S > 1$ and records her last random number '$x$'.
+
+The second player, Julie, continues adding to $S$ different random numbers from the generator until $S > 2$ and records her last random number '$y$'.
+
+The player with the highest number wins and the loser washes the dishes, i.e. if $y > x$ the second player wins.
+
+For example, if the first player draws 0.62 and 0.44, the first player turn ends since $0.62 + 0.44 > 1$ and $x = 0.44$. If the second players draws 0.1, 0.27 and 0.91, the second player turn ends since $0.62 + 0.44 + 0.1 + 0.27 + 0.91 > 2$ and $y = 0.91$. Since $y > x$, the second player wins.
+
+Louise thinks about it for a second, and objects: "That's not fair".
+
+What is the probability that the second player wins? Give your answer rounded to 10 places behind the decimal point in the form 0.abcdefghij
+
+# --hints--
+
+`unfairWager()` should return `0.5276662759`.
+
+```js
+assert.strictEqual(unfairWager(), 0.5276662759);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function unfairWager() {
+
+ return true;
+}
+
+unfairWager();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-437-fibonacci-primitive-roots.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-437-fibonacci-primitive-roots.md
new file mode 100644
index 00000000000..47f1606285d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-437-fibonacci-primitive-roots.md
@@ -0,0 +1,56 @@
+---
+id: 5900f5241000cf542c510036
+title: 'Problem 437: Fibonacci primitive roots'
+challengeType: 1
+forumTopicId: 302108
+dashedName: problem-437-fibonacci-primitive-roots
+---
+
+# --description--
+
+When we calculate $8^n$ modulo 11 for $n = 0$ to 9 we get: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
+
+As we see all possible values from 1 to 10 occur. So 8 is a primitive root of 11.
+
+But there is more:
+
+If we take a closer look we see:
+
+$$\begin{align} & 1 + 8 = 9 \\\\
+ & 8 + 9 = 17 ≡ 6\bmod 11 \\\\ & 9 + 6 = 15 ≡ 4\bmod 11 \\\\
+ & 6 + 4 = 10 \\\\ & 4 + 10 = 14 ≡ 3\bmod 11 \\\\
+ & 10 + 3 = 13 ≡ 2\bmod 11 \\\\ & 3 + 2 = 5 \\\\
+ & 2 + 5 = 7 \\\\ & 5 + 7 = 12 ≡ 1\bmod 11. \end{align}$$
+
+So the powers of 8 mod 11 are cyclic with period 10, and $8^n + 8^{n + 1} ≡ 8^{n + 2} (\text{mod } 11)$. 8 is called a Fibonacci primitive root of 11.
+
+Not every prime has a Fibonacci primitive root. There are 323 primes less than 10000 with one or more Fibonacci primitive roots and the sum of these primes is 1480491.
+
+Find the sum of the primes less than $100\\,000\\,000$ with at least one Fibonacci primitive root.
+
+# --hints--
+
+`fibonacciPrimitiveRoots()` should return `74204709657207`.
+
+```js
+assert.strictEqual(fibonacciPrimitiveRoots(), 74204709657207);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function fibonacciPrimitiveRoots() {
+
+ return true;
+}
+
+fibonacciPrimitiveRoots();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-438-integer-part-of-polynomial-equations-solutions.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-438-integer-part-of-polynomial-equations-solutions.md
new file mode 100644
index 00000000000..05c8bd7d4a5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-438-integer-part-of-polynomial-equations-solutions.md
@@ -0,0 +1,51 @@
+---
+id: 5900f5231000cf542c510034
+title: 'Problem 438: Integer part of polynomial equation''s solutions'
+challengeType: 1
+forumTopicId: 302109
+dashedName: problem-438-integer-part-of-polynomial-equations-solutions
+---
+
+# --description--
+
+For an $n$-tuple of integers $t = (a_1, \ldots, a_n)$, let $(x_1, \ldots, x_n)$ be the solutions of the polynomial equation $x^n + a_1x^{n - 1} + a_2x^{n - 2} + \ldots + a_{n - 1}x + a_n = 0$.
+
+Consider the following two conditions:
+
+- $x_1, \ldots, x_n$ are all real.
+- If $x_1, ..., x_n$ are sorted, $⌊x_i⌋ = i$ for $1 ≤ i ≤ n$. ($⌊·⌋:$ floor function.)
+
+In the case of $n = 4$, there are 12 $n$-tuples of integers which satisfy both conditions.
+
+We define $S(t)$ as the sum of the absolute values of the integers in $t$.
+
+For $n = 4$ we can verify that $\sum S(t) = 2087$ for all $n$-tuples $t$ which satisfy both conditions.
+
+Find $\sum S(t)$ for $n = 7$.
+
+# --hints--
+
+`polynomialIntegerPart()` should return `2046409616809`.
+
+```js
+assert.strictEqual(polynomialIntegerPart(), 2046409616809);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function polynomialIntegerPart() {
+
+ return true;
+}
+
+polynomialIntegerPart();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-439-sum-of-sum-of-divisors.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-439-sum-of-sum-of-divisors.md
new file mode 100644
index 00000000000..bb5669ed088
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-439-sum-of-sum-of-divisors.md
@@ -0,0 +1,46 @@
+---
+id: 5900f5231000cf542c510035
+title: 'Problem 439: Sum of sum of divisors'
+challengeType: 1
+forumTopicId: 302110
+dashedName: problem-439-sum-of-sum-of-divisors
+---
+
+# --description--
+
+Let $d(k)$ be the sum of all divisors of $k$.
+
+We define the function $S(N) = \sum_{i = 1}^N \sum_{j = 1}^N d(i \times j)$.
+
+For example, $S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59$.
+
+You are given that $S({10}^3) = 563\\,576\\,517\\,282$ and $S({10}^5)\bmod {10}^9 = 215\\,766\\,508$.
+
+Find $S({10}^{11})\bmod {10}^9$.
+
+# --hints--
+
+`sumOfSumOfDivisors()` should return `968697378`.
+
+```js
+assert.strictEqual(sumOfSumOfDivisors(), 968697378);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function sumOfSumOfDivisors() {
+
+ return true;
+}
+
+sumOfSumOfDivisors();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-440-gcd-and-tiling.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-440-gcd-and-tiling.md
new file mode 100644
index 00000000000..49afa9608aa
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-440-gcd-and-tiling.md
@@ -0,0 +1,57 @@
+---
+id: 5900f5241000cf542c510037
+title: 'Problem 440: GCD and Tiling'
+challengeType: 1
+forumTopicId: 302112
+dashedName: problem-440-gcd-and-tiling
+---
+
+# --description--
+
+We want to tile a board of length $n$ and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
+
+
+
+For example, here are some of the ways to tile a board of length $n = 8$:
+
+
+
+Let $T(n)$ be the number of ways to tile a board of length $n$ as described above.
+
+For example, $T(1) = 10$ and $T(2) = 101$.
+
+Let $S(L)$ be the triple sum $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ for $1 ≤ a, b, c ≤ L$.
+
+For example:
+
+$$\begin{align} & S(2) = 10\\,444 \\\\
+ & S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280. \end{align}$$
+
+Find $S(2000)\bmod 987\\,898\\,789$.
+
+# --hints--
+
+`gcdAndTiling()` should return `970746056`.
+
+```js
+assert.strictEqual(gcdAndTiling(), 970746056);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function gcdAndTiling() {
+
+ return true;
+}
+
+gcdAndTiling();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-441-the-inverse-summation-of-coprime-couples.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-441-the-inverse-summation-of-coprime-couples.md
new file mode 100644
index 00000000000..9c310a1f18d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-441-the-inverse-summation-of-coprime-couples.md
@@ -0,0 +1,48 @@
+---
+id: 5900f5261000cf542c510038
+title: 'Problem 441: The inverse summation of coprime couples'
+challengeType: 1
+forumTopicId: 302113
+dashedName: problem-441-the-inverse-summation-of-coprime-couples
+---
+
+# --description--
+
+For an integer $M$, we define $R(M)$ as the sum of $\frac{1}{p·q}$ for all the integer pairs $p$ and $q$ which satisfy all of these conditions:
+
+- $1 ≤ p < q ≤ M$
+- $p + q ≥ M$
+- $p$ and $q$ are coprime.
+
+We also define $S(N)$ as the sum of $R(i)$ for $2 ≤ i ≤ N$.
+
+We can verify that $S(2) = R(2) = \frac{1}{2}$, $S(10) ≈ 6.9147$ and $S(100) ≈ 58.2962$.
+
+Find $S({10}^7)$. Give your answer rounded to four decimal places.
+
+# --hints--
+
+`inverseSummationCoprimeCouples()` should return `5000088.8395`.
+
+```js
+assert.strictEqual(inverseSummationCoprimeCouples(), 5000088.8395);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function inverseSummationCoprimeCouples() {
+
+ return true;
+}
+
+inverseSummationCoprimeCouples();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-442-eleven-free-integers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-442-eleven-free-integers.md
new file mode 100644
index 00000000000..9e2e8d90986
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-442-eleven-free-integers.md
@@ -0,0 +1,44 @@
+---
+id: 5900f5271000cf542c510039
+title: 'Problem 442: Eleven-free integers'
+challengeType: 1
+forumTopicId: 302114
+dashedName: problem-442-eleven-free-integers
+---
+
+# --description--
+
+An integer is called eleven-free if its decimal expansion does not contain any substring representing a power of 11 except 1.
+
+For example, 2404 and 13431 are eleven-free, while 911 and 4121331 are not.
+
+Let $E(n)$ be the $n$th positive eleven-free integer. For example, $E(3) = 3$, $E(200) = 213$ and $E(500\\,000) = 531\\,563$.
+
+Find $E({10}^{18})$.
+
+# --hints--
+
+`elevenFreeIntegers()` should return `1295552661530920200`.
+
+```js
+assert.strictEqual(elevenFreeIntegers(), 1295552661530920200);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function elevenFreeIntegers() {
+
+ return true;
+}
+
+elevenFreeIntegers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-443-gcd-sequence.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-443-gcd-sequence.md
new file mode 100644
index 00000000000..17fc8db1cb5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-443-gcd-sequence.md
@@ -0,0 +1,50 @@
+---
+id: 5900f5271000cf542c51003a
+title: 'Problem 443: GCD sequence'
+challengeType: 1
+forumTopicId: 302115
+dashedName: problem-443-gcd-sequence
+---
+
+# --description--
+
+Let $g(n)$ be a sequence defined as follows:
+
+$$\begin{align} & g(4) = 13, \\\\
+ & g(n) = g(n-1) + gcd(n, g(n - 1)) \text{ for } n > 4. \end{align}$$
+
+The first few values are:
+
+$$\begin{array}{l} n & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 & \ldots \\\\
+ g(n) & 13 & 14 & 16 & 17 & 18 & 27 & 28 & 29 & 30 & 31 & 32 & 33 & 34 & 51 & 54 & 55 & 60 & \ldots \end{array}$$
+
+You are given that $g(1\\,000) = 2\\,524$ and $g(1\\,000\\,000) = 2\\,624\\,152$.
+
+Find $g({10}^{15})$.
+
+# --hints--
+
+`gcdSequence()` should return `2744233049300770`.
+
+```js
+assert.strictEqual(gcdSequence(), 2744233049300770);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function gcdSequence() {
+
+ return true;
+}
+
+gcdSequence();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-444-the-roundtable-lottery.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-444-the-roundtable-lottery.md
new file mode 100644
index 00000000000..9e52d4e52b4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-444-the-roundtable-lottery.md
@@ -0,0 +1,61 @@
+---
+id: 5900f52a1000cf542c51003b
+title: 'Problem 444: The Roundtable Lottery'
+challengeType: 1
+forumTopicId: 302116
+dashedName: problem-444-the-roundtable-lottery
+---
+
+# --description--
+
+A group of $p$ people decide to sit down at a round table and play a lottery-ticket trading game. Each person starts off with a randomly-assigned, unscratched lottery ticket. Each ticket, when scratched, reveals a whole-pound prize ranging anywhere from £1 to £$p$, with no two tickets alike. The goal of the game is for each person to maximize his ticket winnings upon leaving the game.
+
+An arbitrary person is chosen to be the first player. Going around the table, each player has only one of two options:
+
+1. The player can scratch his ticket and reveal its worth to everyone at the table.
+2. The player can trade his unscratched ticket for a previous player's scratched ticket, and then leave the game with that ticket. The previous player then scratches his newly-acquired ticket and reveals its worth to everyone at the table.
+
+The game ends once all tickets have been scratched. All players still remaining at the table must leave with their currently-held tickets.
+
+Assume that each player uses the optimal strategy for maximizing the expected value of his ticket winnings.
+
+Let $E(p)$ represent the expected number of players left at the table when the game ends in a game consisting of $p$ players (e.g. $E(111) = 5.2912$ when rounded to 5 significant digits).
+
+Let $S_1(N) = \displaystyle\sum_{p = 1}^N E(p)$.
+
+Let $S_k(N) = \displaystyle\sum_{p = 1}^N S_{k - 1}(p)$ for $k > 1$.
+
+Find $S_{20}({10}^{14})$ and write the answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent. For example, the answer for $S_3(100)$ would be `5.983679014e5`.
+
+# --hints--
+
+`roundtableLottery()` should return a string.
+
+```js
+assert(typeof roundtableLottery() === 'string');
+```
+
+`roundtableLottery()` should return the string `1.200856722e263`.
+
+```js
+assert.strictEqual(roundtableLottery(), '1.200856722e263');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function roundtableLottery() {
+
+ return true;
+}
+
+roundtableLottery();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-445-retractions-a.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-445-retractions-a.md
new file mode 100644
index 00000000000..841d3796c7d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-445-retractions-a.md
@@ -0,0 +1,50 @@
+---
+id: 5900f52a1000cf542c51003c
+title: 'Problem 445: Retractions A'
+challengeType: 1
+forumTopicId: 302117
+dashedName: problem-445-retractions-a
+---
+
+# --description--
+
+For every integer $n > 1$, the family of functions $f_{n, a, b}$ is defined by:
+
+$f_{n, a, b}(x) ≡ ax + b\bmod n$ for $a, b, x$ integer and $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$.
+
+We will call $f_{n, a, b}$ a retraction if $f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ for every $0 \le x \lt n$.
+
+Let $R(n)$ be the number of retractions for $n$.
+
+You are given that
+
+$$\sum_{k = 1}^{99\\,999} R(\displaystyle\binom{100\\,000}{k}) \equiv 628\\,701\\,600\bmod 1\\,000\\,000\\,007$$
+
+Find $$\sum_{k = 1}^{9\\,999\\,999} R(\displaystyle\binom{10\\,000\\,000}{k})$$ Give your answer modulo $1\\,000\\,000\\,007$.
+
+# --hints--
+
+`retractionsA()` should return `659104042`.
+
+```js
+assert.strictEqual(retractionsA(), 659104042);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function retractionsA() {
+
+ return true;
+}
+
+retractionsA();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-446-retractions-b.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-446-retractions-b.md
new file mode 100644
index 00000000000..f1919d426f5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-446-retractions-b.md
@@ -0,0 +1,50 @@
+---
+id: 5900f52c1000cf542c51003d
+title: 'Problem 446: Retractions B'
+challengeType: 1
+forumTopicId: 302118
+dashedName: problem-446-retractions-b
+---
+
+# --description--
+
+For every integer $n > 1$, the family of functions $f_{n, a, b}$ is defined by:
+
+$f_{n, a, b}(x) ≡ ax + b\bmod n$ for $a, b, x$ integer and $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$.
+
+We will call $f_{n, a, b}$ a retraction if $f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ for every $0 \le x \lt n$.
+
+Let $R(n)$ be the number of retractions for $n$.
+
+$F(N) = \displaystyle\sum_{n = 1}^N R(n^4 + 4)$.
+
+$F(1024) = 77\\,532\\,377\\,300\\,600$.
+
+Find $F({10}^7)$. Give your answer modulo $1\\,000\\,000\\,007$.
+
+# --hints--
+
+`retractionsB()` should return `907803852`.
+
+```js
+assert.strictEqual(retractionsB(), 907803852);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function retractionsB() {
+
+ return true;
+}
+
+retractionsB();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-447-retractions-c.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-447-retractions-c.md
new file mode 100644
index 00000000000..882f61f24d0
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-447-retractions-c.md
@@ -0,0 +1,50 @@
+---
+id: 5900f52c1000cf542c51003e
+title: 'Problem 447: Retractions C'
+challengeType: 1
+forumTopicId: 302119
+dashedName: problem-447-retractions-c
+---
+
+# --description--
+
+For every integer $n > 1$, the family of functions $f_{n, a, b}$ is defined by:
+
+$f_{n, a, b}(x) ≡ ax + b\bmod n$ for $a, b, x$ integer and $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$.
+
+We will call $f_{n, a, b}$ a retraction if $f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ for every $0 \le x \lt n$.
+
+Let $R(n)$ be the number of retractions for $n$.
+
+$F(N) = \displaystyle\sum_{n = 2}^N R(n)$.
+
+$F({10}^7) ≡ 638\\,042\\,271\bmod 1\\,000\\,000\\,007$.
+
+Find $F({10}^{14})$. Give your answer modulo $1\\,000\\,000\\,007$.
+
+# --hints--
+
+`retractionsC()` should return `530553372`.
+
+```js
+assert.strictEqual(retractionsC(), 530553372);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function retractionsC() {
+
+ return true;
+}
+
+retractionsC();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-448-average-least-common-multiple.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-448-average-least-common-multiple.md
new file mode 100644
index 00000000000..26643961a3e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-448-average-least-common-multiple.md
@@ -0,0 +1,48 @@
+---
+id: 5900f52c1000cf542c51003f
+title: 'Problem 448: Average least common multiple'
+challengeType: 1
+forumTopicId: 302120
+dashedName: problem-448-average-least-common-multiple
+---
+
+# --description--
+
+The function $lcm(a, b)$ denotes the least common multiple of $a$ and $b$.
+
+Let $A(n)$ be the average of the values of $lcm(n, i)$ for $1 ≤ i ≤ n$.
+
+E.g: $A(2) = \frac{2 + 2}{2} = 2$ and $A(10) = \frac{10 + 10 + 30 + 20 + 10 + 30 + 70 + 40 + 90 + 10}{10} = 32$.
+
+Let $S(n) = \sum A(k)$ for $1 ≤ k ≤ n$.
+
+$S(100) = 122\\,726$.
+
+Find $S(99\\,999\\,999\\,019)\bmod 999\\,999\\,017$.
+
+# --hints--
+
+`averageLCM()` should return `106467648`.
+
+```js
+assert.strictEqual(averageLCM(), 106467648);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function averageLCM() {
+
+ return true;
+}
+
+averageLCM();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-449-chocolate-covered-candy.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-449-chocolate-covered-candy.md
new file mode 100644
index 00000000000..f312fd4ab49
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-449-chocolate-covered-candy.md
@@ -0,0 +1,46 @@
+---
+id: 5900f52d1000cf542c510040
+title: 'Problem 449: Chocolate covered candy'
+challengeType: 1
+forumTopicId: 302121
+dashedName: problem-449-chocolate-covered-candy
+---
+
+# --description--
+
+Phil the confectioner is making a new batch of chocolate covered candy. Each candy centre is shaped like an ellipsoid of revolution defined by the equation: $b^2x^2 + b^2y^2 + a^2z^2 = a^2b^2$.
+
+Phil wants to know how much chocolate is needed to cover one candy centre with a uniform coat of chocolate one millimeter thick.
+
+If $a = 1$ mm and $b = 1$ mm, the amount of chocolate required is $\frac{28}{3} \pi$ mm3
+
+If $a = 2$ mm and $b = 1$ mm, the amount of chocolate required is approximately 60.35475635 mm3.
+
+Find the amount of chocolate in mm3 required if $a = 3$ mm and $b = 1$ mm. Give your answer as the number rounded to 8 decimal places behind the decimal point.
+
+# --hints--
+
+`chocolateCoveredCandy()` should return `103.37870096`.
+
+```js
+assert.strictEqual(chocolateCoveredCandy(), 103.37870096);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function chocolateCoveredCandy() {
+
+ return true;
+}
+
+chocolateCoveredCandy();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-450-hypocycloid-and-lattice-points.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-450-hypocycloid-and-lattice-points.md
new file mode 100644
index 00000000000..9bfd7f5d15a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-450-hypocycloid-and-lattice-points.md
@@ -0,0 +1,63 @@
+---
+id: 5900f52e1000cf542c510041
+title: 'Problem 450: Hypocycloid and Lattice points'
+challengeType: 1
+forumTopicId: 302123
+dashedName: problem-450-hypocycloid-and-lattice-points
+---
+
+# --description--
+
+A hypocycloid is the curve drawn by a point on a small circle rolling inside a larger circle. The parametric equations of a hypocycloid centered at the origin, and starting at the right most point is given by:
+
+$$x(t) = (R - r) \cos(t) + r \cos(\frac{R - r}{r}t)$$
+
+$$y(t) = (R - r) \sin(t) - r \sin(\frac{R - r}{r} t)$$
+
+Where $R$ is the radius of the large circle and $r$ the radius of the small circle.
+
+Let $C(R, r)$ be the set of distinct points with integer coordinates on the hypocycloid with radius $R$ and $r$ and for which there is a corresponding value of $t$ such that $\sin(t)$ and $\cos(t)$ are rational numbers.
+
+Let $S(R, r) = \sum\_{(x,y) \in C(R, r)} |x| + |y|$ be the sum of the absolute values of the $x$ and $y$ coordinates of the points in $C(R, r)$.
+
+Let $T(N) = \sum_{R = 3}^N \sum_{r=1}^{\left\lfloor \frac{R - 1}{2} \right\rfloor} S(R, r)$ be the sum of $S(R, r)$ for $R$ and $r$ positive integers, $R\leq N$ and $2r < R$.
+
+You are given:
+
+$$\begin{align} C(3, 1) = & \\{(3, 0), (-1, 2), (-1,0), (-1,-2)\\} \\\\
+ C(2500, 1000) = & \\{(2500, 0), (772, 2376), (772, -2376), (516, 1792), (516, -1792), (500, 0), (68, 504), \\\\ &(68, -504),(-1356, 1088), (-1356, -1088), (-1500, 1000), (-1500, -1000)\\} \end{align}$$
+
+**Note:** (-625, 0) is not an element of $C(2500, 1000)$ because $\sin(t)$ is not a rational number for the corresponding values of $t$.
+
+$S(3, 1) = (|3| + |0|) + (|-1| + |2|) + (|-1| + |0|) + (|-1| + |-2|) = 10$
+
+$T(3) = 10$; $T(10) = 524$; $T(100) = 580\\,442$; $T({10}^3) = 583\\,108\\,600$.
+
+Find $T({10}^6)$.
+
+# --hints--
+
+`hypocycloidAndLatticePoints()` should return `583333163984220900`.
+
+```js
+assert.strictEqual(hypocycloidAndLatticePoints(), 583333163984220900);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function hypocycloidAndLatticePoints() {
+
+ return true;
+}
+
+hypocycloidAndLatticePoints();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-451-modular-inverses.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-451-modular-inverses.md
new file mode 100644
index 00000000000..39ebff17846
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-451-modular-inverses.md
@@ -0,0 +1,55 @@
+---
+id: 5900f5311000cf542c510042
+title: 'Problem 451: Modular inverses'
+challengeType: 1
+forumTopicId: 302124
+dashedName: problem-451-modular-inverses
+---
+
+# --description--
+
+Consider the number 15.
+
+There are eight positive numbers less than 15 which are coprime to 15: 1, 2, 4, 7, 8, 11, 13, 14.
+
+The modular inverses of these numbers modulo 15 are: 1, 8, 4, 13, 2, 11, 7, 14 because
+
+$$\begin{align} & 1 \times 1\bmod 15 = 1 \\\\
+ & 2 \times 8 = 16\bmod 15 = 1 \\\\ & 4 \times 4 = 16\bmod 15 = 1 \\\\
+ & 7 \times 13 = 91\bmod 15 = 1 \\\\ & 11 \times 11 = 121\bmod 15 = 1 \\\\
+ & 14 \times 14 = 196\bmod 15 = 1 \end{align}$$
+
+Let $I(n)$ be the largest positive number $m$ smaller than $n - 1$ such that the modular inverse of $m$ modulo $n$ equals $m$ itself.
+
+So $I(15) = 11$.
+
+Also $I(100) = 51$ and $I(7) = 1$.
+
+Find $\sum I(n)$ for $3 ≤ n ≤ 2 \times {10}^7$
+
+# --hints--
+
+`modularInverses()` should return `153651073760956`.
+
+```js
+assert.strictEqual(modularInverses(), 153651073760956);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function modularInverses() {
+
+ return true;
+}
+
+modularInverses();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-452-long-products.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-452-long-products.md
new file mode 100644
index 00000000000..abb043bcebe
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-452-long-products.md
@@ -0,0 +1,44 @@
+---
+id: 5900f5311000cf542c510043
+title: 'Problem 452: Long Products'
+challengeType: 1
+forumTopicId: 302125
+dashedName: problem-452-long-products
+---
+
+# --description--
+
+Define $F(m, n)$ as the number of $n$-tuples of positive integers for which the product of the elements doesn't exceed $m$.
+
+$F(10, 10) = 571$.
+
+$F({10}^6, {10}^6)\bmod 1\\,234\\,567\\,891 = 252\\,903\\,833$.
+
+Find $F({10}^9, {10}^9)\bmod 1\\,234\\,567\\,891$.
+
+# --hints--
+
+`longProducts()` should return `345558983`.
+
+```js
+assert.strictEqual(longProducts(), 345558983);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function longProducts() {
+
+ return true;
+}
+
+longProducts();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-453-lattice-quadrilaterals.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-453-lattice-quadrilaterals.md
new file mode 100644
index 00000000000..f809ebc60a5
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-453-lattice-quadrilaterals.md
@@ -0,0 +1,48 @@
+---
+id: 5900f5311000cf542c510044
+title: 'Problem 453: Lattice Quadrilaterals'
+challengeType: 1
+forumTopicId: 302126
+dashedName: problem-453-lattice-quadrilaterals
+---
+
+# --description--
+
+A simple quadrilateral is a polygon that has four distinct vertices, has no straight angles and does not self-intersect.
+
+Let $Q(m, n)$ be the number of simple quadrilaterals whose vertices are lattice points with coordinates ($x$, $y$) satisfying $0 ≤ x ≤ m$ and $0 ≤ y ≤ n$.
+
+For example, $Q(2, 2) = 94$ as can be seen below:
+
+
+
+It can also be verified that $Q(3, 7) = 39\\,590$, $Q(12, 3) = 309\\,000$ and $Q(123, 45) = 70\\,542\\,215\\,894\\,646$.
+
+Find $Q(12\\,345, 6\\,789)\bmod 135\\,707\\,531$.
+
+# --hints--
+
+`latticeQuadrilaterals()` should return `104354107`.
+
+```js
+assert.strictEqual(latticeQuadrilaterals(), 104354107);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function latticeQuadrilaterals() {
+
+ return true;
+}
+
+latticeQuadrilaterals();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-454-diophantine-reciprocals-iii.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-454-diophantine-reciprocals-iii.md
new file mode 100644
index 00000000000..b2fca3b4a6b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-454-diophantine-reciprocals-iii.md
@@ -0,0 +1,46 @@
+---
+id: 5900f5331000cf542c510045
+title: 'Problem 454: Diophantine reciprocals III'
+challengeType: 1
+forumTopicId: 302127
+dashedName: problem-454-diophantine-reciprocals-iii
+---
+
+# --description--
+
+In the following equation $x$, $y$, and $n$ are positive integers.
+
+$$\frac{1}{x} + \frac{1}{y} = \frac{1}{n}$$
+
+For a limit $L$ we define $F(L)$ as the number of solutions which satisfy $x < y ≤ L$.
+
+We can verify that $F(15) = 4$ and $F(1000) = 1069$.
+
+Find $F({10}^{12})$.
+
+# --hints--
+
+`diophantineReciprocalsThree()` should return `5435004633092`.
+
+```js
+assert.strictEqual(diophantineReciprocalsThree(), 5435004633092);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function diophantineReciprocalsThree() {
+
+ return true;
+}
+
+diophantineReciprocalsThree();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-455-powers-with-trailing-digits.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-455-powers-with-trailing-digits.md
new file mode 100644
index 00000000000..8e453a983c2
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-455-powers-with-trailing-digits.md
@@ -0,0 +1,46 @@
+---
+id: 5900f5331000cf542c510046
+title: 'Problem 455: Powers With Trailing Digits'
+challengeType: 1
+forumTopicId: 302129
+dashedName: problem-455-powers-with-trailing-digits
+---
+
+# --description--
+
+Let $f(n)$ be the largest positive integer $x$ less than ${10}^9$ such that the last 9 digits of $n^x$ form the number $x$ (including leading zeros), or zero if no such integer exists.
+
+For example:
+
+$$\begin{align} & f(4) = 411\\,728\\,896 (4^{411\\,728\\,896} = ...490\underline{411728896}) \\\\
+ & f(10) = 0 \\\\ & f(157) = 743\\,757 (157^{743\\,757} = ...567\underline{000743757}) \\\\
+ & Σf(n), 2 ≤ n ≤ 103 = 442\\,530\\,011\\,399 \end{align}$$
+
+Find $\sum f(n)$, $2 ≤ n ≤ {10}^6$.
+
+# --hints--
+
+`powersWithTrailingDigits()` should return `450186511399999`.
+
+```js
+assert.strictEqual(powersWithTrailingDigits(), 450186511399999);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function powersWithTrailingDigits() {
+
+ return true;
+}
+
+powersWithTrailingDigits();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-456-triangles-containing-the-origin-ii.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-456-triangles-containing-the-origin-ii.md
new file mode 100644
index 00000000000..b622b8ac411
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-456-triangles-containing-the-origin-ii.md
@@ -0,0 +1,52 @@
+---
+id: 5900f5351000cf542c510047
+title: 'Problem 456: Triangles containing the origin II'
+challengeType: 1
+forumTopicId: 302130
+dashedName: problem-456-triangles-containing-the-origin-ii
+---
+
+# --description--
+
+Define:
+
+$$\begin{align} & x_n = ({1248}^n\bmod 32323) - 16161 \\\\
+ & y_n = ({8421}^n\bmod 30103) - 15051 \\\\ & P_n = \\{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\\} \end{align}$$
+
+For example, $$P_8 = \\{(-14913, -6630), (-10161, 5625), (5226, 11896), (8340, -10778), (15852, -5203), (-15165, 11295), (-1427, -14495), (12407, 1060)\\}$$
+
+Let $C(n)$ be the number of triangles whose vertices are in $P_n$ which contain the origin in the interior.
+
+Examples:
+
+$$\begin{align} & C(8) = 20 \\\\
+ & C(600) = 8\\,950\\,634 \\\\ & C(40\\,000) = 2\\,666\\,610\\,948\\,988 \end{align}$$
+
+Find $C(2\\,000\\,000)$.
+
+# --hints--
+
+`trianglesContainingOriginTwo()` should return `333333208685971500`.
+
+```js
+assert.strictEqual(trianglesContainingOriginTwo(), 333333208685971500);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function trianglesContainingOriginTwo() {
+
+ return true;
+}
+
+trianglesContainingOriginTwo();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-457-a-polynomial-modulo-the-square-of-a-prime.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-457-a-polynomial-modulo-the-square-of-a-prime.md
new file mode 100644
index 00000000000..b187b6c488a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-457-a-polynomial-modulo-the-square-of-a-prime.md
@@ -0,0 +1,46 @@
+---
+id: 5900f5361000cf542c510048
+title: 'Problem 457: A polynomial modulo the square of a prime'
+challengeType: 1
+forumTopicId: 302131
+dashedName: problem-457-a-polynomial-modulo-the-square-of-a-prime
+---
+
+# --description--
+
+Let $f(n) = n^2 - 3n - 1$.
+
+Let $p$ be a prime.
+
+Let $R(p)$ be the smallest positive integer $n$ such that $f(n)\bmod p^2 = 0$ if such an integer $n$ exists, otherwise $R(p) = 0$.
+
+Let $SR(L)$ be $\sum R(p)$ for all primes not exceeding $L$.
+
+Find $SR({10}^7)$.
+
+# --hints--
+
+`polynomialModuloSquareOfPrime()` should return `2647787126797397000`.
+
+```js
+assert.strictEqual(polynomialModuloSquareOfPrime(), 2647787126797397000);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function polynomialModuloSquareOfPrime() {
+
+ return true;
+}
+
+polynomialModuloSquareOfPrime();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-458-permutations-of-project.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-458-permutations-of-project.md
new file mode 100644
index 00000000000..c368503124d
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-458-permutations-of-project.md
@@ -0,0 +1,44 @@
+---
+id: 5900f5361000cf542c510049
+title: 'Problem 458: Permutations of Project'
+challengeType: 1
+forumTopicId: 302132
+dashedName: problem-458-permutations-of-project
+---
+
+# --description--
+
+Consider the alphabet $A$ made out of the letters of the word `project`: $A = \\{c, e, j, o, p, r, t\\}$.
+
+Let $T(n)$ be the number of strings of length $n$ consisting of letters from $A$ that do not have a substring that is one of the 5040 permutations of `project`.
+
+$T(7) = 7^7 - 7! = 818\\,503$.
+
+Find $T({10}^{12})$. Give the last 9 digits of your answer.
+
+# --hints--
+
+`permutationsOfProject()` should return `423341841`.
+
+```js
+assert.strictEqual(permutationsOfProject(), 423341841);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function permutationsOfProject() {
+
+ return true;
+}
+
+permutationsOfProject();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-459-flipping-game.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-459-flipping-game.md
new file mode 100644
index 00000000000..13473d922bf
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-459-flipping-game.md
@@ -0,0 +1,62 @@
+---
+id: 5900f5371000cf542c51004a
+title: 'Problem 459: Flipping game'
+challengeType: 1
+forumTopicId: 302133
+dashedName: problem-459-flipping-game
+---
+
+# --description--
+
+The flipping game is a two player game played on a $N$ by $N$ square board.
+
+Each square contains a disk with one side white and one side black.
+
+The game starts with all disks showing their white side.
+
+A turn consists of flipping all disks in a rectangle with the following properties:
+
+- the upper right corner of the rectangle contains a white disk
+- the rectangle width is a perfect square (1, 4, 9, 16, ...)
+- the rectangle height is a triangular number (1, 3, 6, 10, ...)
+
+
+
+Players alternate turns. A player wins by turning the grid all black.
+
+Let $W(N)$ be the number of winning moves for the first player on a $N$ by $N$ board with all disks white, assuming perfect play.
+
+$W(1) = 1$, $W(2) = 0$, $W(5) = 8$ and $W({10}^2) = 31\\,395$.
+
+For $N = 5$, the first player's eight winning first moves are:
+
+
+
+Find $W({10}^6)$.
+
+# --hints--
+
+`flippingGame()` should return `3996390106631`.
+
+```js
+assert.strictEqual(flippingGame(), 3996390106631);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function flippingGame() {
+
+ return true;
+}
+
+flippingGame();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-460-an-ant-on-the-move.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-460-an-ant-on-the-move.md
new file mode 100644
index 00000000000..2bb68f203f4
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-460-an-ant-on-the-move.md
@@ -0,0 +1,57 @@
+---
+id: 5900f5381000cf542c51004b
+title: 'Problem 460: An ant on the move'
+challengeType: 1
+forumTopicId: 302135
+dashedName: problem-460-an-ant-on-the-move
+---
+
+# --description--
+
+On the Euclidean plane, an ant travels from point $A(0, 1)$ to point $B(d, 1)$ for an integer $d$.
+
+In each step, the ant at point ($x_0$, $y_0$) chooses one of the lattice points ($x_1$, $y_1$) which satisfy $x_1 ≥ 0$ and $y_1 ≥ 1$ and goes straight to ($x_1$, $y_1$) at a constant velocity $v$. The value of $v$ depends on $y_0$ and $y_1$ as follows:
+
+- If $y_0 = y_1$, the value of $v$ equals $y_0$.
+- If $y_0 ≠ y_1$, the value of $v$ equals $\frac{y_1 - y_0}{\ln y_1 - \ln y_0}$.
+
+The left image is one of the possible paths for $d = 4$. First the ant goes from $A(0, 1)$ to $P_1(1, 3)$ at velocity $\frac{3 - 1}{\ln 3 - \ln 1} ≈ 1.8205$. Then the required time is $\frac{\sqrt{5}}{1.820} ≈ 1.2283$.
+
+From $P_1(1, 3)$ to $P_2(3, 3)$ the ant travels at velocity 3 so the required time is $\frac{2}{3} ≈ 0.6667$. From $P_2(3, 3)$ to $B(4, 1)$ the ant travels at velocity $\frac{1 - 3}{\ln 1 - \ln 3} ≈ 1.8205$ so the required time is $\frac{\sqrt{5}}{1.8205} ≈ 1.2283$.
+
+Thus the total required time is $1.2283 + 0.6667 + 1.2283 = 3.1233$.
+
+The right image is another path. The total required time is calculated as $0.98026 + 1 + 0.98026 = 2.96052$. It can be shown that this is the quickest path for $d = 4$.
+
+
+
+Let $F(d)$ be the total required time if the ant chooses the quickest path. For example, $F(4) ≈ 2.960\\,516\\,287$. We can verify that $F(10) ≈ 4.668\\,187\\,834$ and $F(100) ≈ 9.217\\,221\\,972$.
+
+Find $F(10\\,000)$. Give your answer rounded to nine decimal places.
+
+# --hints--
+
+`antOnTheMove()` should return `18.420738199`.
+
+```js
+assert.strictEqual(antOnTheMove(), 18.420738199);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function antOnTheMove() {
+
+ return true;
+}
+
+antOnTheMove();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-461-almost-pi.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-461-almost-pi.md
new file mode 100644
index 00000000000..1ff7e49ee6b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-461-almost-pi.md
@@ -0,0 +1,153 @@
+---
+id: 5900f53a1000cf542c51004c
+title: 'Problem 461: Almost Pi'
+challengeType: 1
+forumTopicId: 302136
+dashedName: problem-461-almost-pi
+---
+
+# --description--
+
+Let `f(k, n)` = $e^\frac{k}{n} - 1$, for all non-negative integers `k`.
+
+Remarkably, `f(6, 200) + f(75, 200) + f(89, 200) + f(226, 200)` = 3.1415926… ≈ π.
+
+In fact, it is the best approximation of π of the form `f(a, 200) + f(b, 200) + f(c, 200) + f(d, 200)`.
+
+Let `almostPi(n)` = a2 + b2 + c2 + d2 for a, b, c, d that minimize the error: $\lvert f(a,n) + f(b,n) + f(c,n) + f(d,n) - \Pi\rvert$
+
+You are given `almostPi(200)` = 62 + 752 + 892 + 2262 = 64658.
+
+# --hints--
+
+`almostPi` should be a function.
+
+```js
+assert(typeof almostPi === 'function')
+```
+
+`almostPi` should return a number.
+
+```js
+assert.strictEqual(typeof almostPi(10), 'number');
+```
+
+`almostPi(29)` should return `1208`.
+
+```js
+assert.strictEqual(almostPi(29), 1208);
+```
+
+`almostPi(50)` should return `4152`.
+
+```js
+assert.strictEqual(almostPi(50), 4152);
+```
+
+`almostPi(200)` should return `64658`.
+
+```js
+assert.strictEqual(almostPi(200), 64658);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function almostPi(n) {
+
+ return true;
+}
+```
+
+# --solutions--
+
+```js
+function almostPi(n) {
+
+ // Find all possible values where f(k, n) <= PI
+ const f = [];
+ let max = 0;
+ while (1) {
+ let current = Math.exp(max / n) - 1;
+
+ if (current > Math.PI) break;
+
+ f.push(current);
+ ++max;
+ }
+
+ // Get all pairs where f[i] + f[j] <= PI
+ const pairs = [];
+ for (let i = 0; i < max; ++i) {
+ for (let j = 0; j < max; ++j) {
+ if (f[i] + f[j] > Math.PI) break;
+ pairs.push(f[i] + f[j]);
+ }
+ }
+
+ // Sort all values
+ pairs.sort((a, b) => a - b);
+
+ // Optimal Value for (a + b)
+ let left = 0;
+ // Optimal Value for (c + d)
+ let right = 0;
+ // minimum error with Math.abs(a + b - Math.PI)
+ let minError = Math.PI;
+
+ // Binary Search for the best match
+ for (let i = 0; i < pairs.length; ++i) {
+ let current = pairs[i];
+ let need = Math.PI - current;
+
+ if (need < current) break;
+
+ let match;
+ for (let i = 1; i < pairs.length; ++i) {
+ if (pairs[i] > need) {
+ match = i;
+ break;
+ }
+ }
+
+ let error = Math.abs(need - pairs[match]);
+ if (error < minError)
+ {
+ minError = error;
+ left = i;
+ right = match;
+ }
+
+ --match;
+ error = Math.abs(need - pairs[match]);
+ if (error < minError) {
+ minError = error;
+ left = i;
+ right = match;
+ }
+ }
+
+ let a, b, c, d;
+
+ OuterLoop1:
+ for (a = 0; a < max; ++a) {
+ for (b = a; b < max; ++b) {
+ if (pairs[left] == f[a] + f[b]) {
+ break OuterLoop1;
+ }
+ }
+ }
+
+ OuterLoop2:
+ for (c = 0; c < max; ++c) {
+ for (d = c; d < max; ++d) {
+ if (pairs[right] == f[c] + f[d]) {
+ break OuterLoop2;
+ }
+ }
+ }
+ return a*a + b*b + c*c + d*d;
+}
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-462-permutation-of-3-smooth-numbers.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-462-permutation-of-3-smooth-numbers.md
new file mode 100644
index 00000000000..b17dc1befcd
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-462-permutation-of-3-smooth-numbers.md
@@ -0,0 +1,58 @@
+---
+id: 5900f53b1000cf542c51004d
+title: 'Problem 462: Permutation of 3-smooth numbers'
+challengeType: 1
+forumTopicId: 302137
+dashedName: problem-462-permutation-of-3-smooth-numbers
+---
+
+# --description--
+
+A 3-smooth number is an integer which has no prime factor larger than 3. For an integer $N$, we define $S(N)$ as the set of 3-smooth numbers less than or equal to $N$. For example, $S(20) = \\{1, 2, 3, 4, 6, 8, 9, 12, 16, 18\\}$.
+
+We define $F(N)$ as the number of permutations of $S(N)$ in which each element comes after all of its proper divisors.
+
+This is one of the possible permutations for $N = 20$.
+
+- 1, 2, 4, 3, 9, 8, 16, 6, 18, 12.
+
+This is not a valid permutation because 12 comes before its divisor 6.
+
+- 1, 2, 4, 3, 9, 8, 12, 16, 6, 18.
+
+We can verify that $F(6) = 5$, $F(8) = 9$, $F(20) = 450$ and $F(1000) ≈ 8.8521816557e\\,21$.
+
+Find $F({10}^{18})$. Give as your answer as a string in its scientific notation rounded to ten digits after the decimal point. When giving your answer, use a lowercase `e` to separate mantissa and exponent. E.g. if the answer is $112\\,233\\,445\\,566\\,778\\,899$ then the answer format would be `1.1223344557e17`.
+
+# --hints--
+
+`permutationOf3SmoothNumbers()` should return a string.
+
+```js
+assert.strictEqual(typeof permutationOf3SmoothNumbers() === 'string');
+```
+
+`permutationOf3SmoothNumbers()` should return the string `5.5350769703e1512`.
+
+```js
+assert.strictEqual(permutationOf3SmoothNumbers(), '5.5350769703e1512');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function permutationOf3SmoothNumbers() {
+
+ return true;
+}
+
+permutationOf3SmoothNumbers();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-463-a-weird-recurrence-relation.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-463-a-weird-recurrence-relation.md
new file mode 100644
index 00000000000..a8e3607195e
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-463-a-weird-recurrence-relation.md
@@ -0,0 +1,48 @@
+---
+id: 5900f53c1000cf542c51004e
+title: 'Problem 463: A weird recurrence relation'
+challengeType: 1
+forumTopicId: 302138
+dashedName: problem-463-a-weird-recurrence-relation
+---
+
+# --description--
+
+The function $f$ is defined for all positive integers as follows:
+
+$$\begin{align} & f(1) = 1 \\\\
+ & f(3) = 3 \\\\ & f(2n) = f(n) \\\\
+ & f(4n + 1) = 2f(2n + 1) - f(n) \\\\ & f(4n + 3) = 3f(2n + 1) - 2f(n) \end{align}$$
+
+The function $S(n)$ is defined as $\sum_{i=1}^{n} f(i)$.
+
+$S(8) = 22$ and $S(100) = 3604$.
+
+Find $S(3^{37})$. Give the last 9 digits of your answer.
+
+# --hints--
+
+`weirdRecurrenceRelation()` should return `808981553`.
+
+```js
+assert.strictEqual(weirdRecurrenceRelation(), 808981553);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function weirdRecurrenceRelation() {
+
+ return true;
+}
+
+weirdRecurrenceRelation();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-464-mbius-function-and-intervals.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-464-mbius-function-and-intervals.md
new file mode 100644
index 00000000000..d293fcda274
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-464-mbius-function-and-intervals.md
@@ -0,0 +1,57 @@
+---
+id: 5900f53d1000cf542c51004f
+title: 'Problem 464: Möbius function and intervals'
+challengeType: 1
+forumTopicId: 302139
+dashedName: problem-464-mbius-function-and-intervals
+---
+
+# --description--
+
+The Möbius function, denoted $μ(n)$, is defined as:
+
+- $μ(n) = (-1)^{ω(n)}$ if $n$ is squarefree (where $ω(n)$ is the number of distinct prime factors of $n$)
+- $μ(n) = 0$ if $n$ is not squarefree.
+
+Let $P(a, b)$ be the number of integers $n$ in the interval $[a, b]$ such that $μ(n) = 1$.
+
+Let $N(a, b)$ be the number of integers $n$ in the interval $[a, b]$ such that $μ(n) = -1$.
+
+For example, $P(2, 10) = 2$ and $N(2, 10) = 4$.
+
+Let $C(n)$ be the number of integer pairs $(a, b)$ such that:
+
+- $1 ≤ a ≤ b ≤ n$,
+- $99 \times N(a, b) ≤ 100 \times P(a, b)$, and
+- $99 \times P(a, b) ≤ 100 \times N(a, b)$.
+
+For example, $C(10) = 13$, $C(500) = 16\\,676$ and $C(10\\,000) = 20\\,155\\,319$.
+
+Find $C(20\\,000\\,000)$.
+
+# --hints--
+
+`mobiusFunctionAndIntervals()` should return `198775297232878`.
+
+```js
+assert.strictEqual(mobiusFunctionAndIntervals(), 198775297232878);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function mobiusFunctionAndIntervals() {
+
+ return true;
+}
+
+mobiusFunctionAndIntervals();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-465-polar-polygons.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-465-polar-polygons.md
new file mode 100644
index 00000000000..57ad5b291d6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-465-polar-polygons.md
@@ -0,0 +1,54 @@
+---
+id: 5900f53d1000cf542c510050
+title: 'Problem 465: Polar polygons'
+challengeType: 1
+forumTopicId: 302140
+dashedName: problem-465-polar-polygons
+---
+
+# --description--
+
+The kernel of a polygon is defined by the set of points from which the entire polygon's boundary is visible. We define a polar polygon as a polygon for which the origin is strictly contained inside its kernel.
+
+For this problem, a polygon can have collinear consecutive vertices. However, a polygon still cannot have self-intersection and cannot have zero area.
+
+For example, only the first of the following is a polar polygon (the kernels of the second, third, and fourth do not strictly contain the origin, and the fifth does not have a kernel at all):
+
+
+
+Notice that the first polygon has three consecutive collinear vertices.
+
+Let $P(n)$ be the number of polar polygons such that the vertices $(x, y)$ have integer coordinates whose absolute values are not greater than $n$.
+
+Note that polygons should be counted as different if they have different set of edges, even if they enclose the same area. For example, the polygon with vertices [(0,0), (0,3), (1,1), (3,0)] is distinct from the polygon with vertices [(0,0), (0,3), (1,1), (3,0), (1,0)].
+
+For example, $P(1) = 131$, $P(2) = 1\\,648\\,531$, $P(3) = 1\\,099\\,461\\,296\\,175$ and $P(343)\bmod 1\\,000\\,000\\,007 = 937\\,293\\,740$.
+
+Find $P(7^{13})\bmod 1\\,000\\,000\\,007$.
+
+# --hints--
+
+`polarPolygons()` should return `585965659`.
+
+```js
+assert.strictEqual(polarPolygons(), 585965659);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function polarPolygons() {
+
+ return true;
+}
+
+polarPolygons();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-466-distinct-terms-in-a-multiplication-table.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-466-distinct-terms-in-a-multiplication-table.md
new file mode 100644
index 00000000000..cfefe6e7b9f
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-466-distinct-terms-in-a-multiplication-table.md
@@ -0,0 +1,54 @@
+---
+id: 5900f53e1000cf542c510051
+title: 'Problem 466: Distinct terms in a multiplication table'
+challengeType: 1
+forumTopicId: 302141
+dashedName: problem-466-distinct-terms-in-a-multiplication-table
+---
+
+# --description--
+
+Let $P(m,n)$ be the number of distinct terms in an $m×n$ multiplication table.
+
+For example, a 3×4 multiplication table looks like this:
+
+$$\begin{array}{c} × & \mathbf{1} & \mathbf{2} & \mathbf{3} & \mathbf{4} \\\\
+ \mathbf{1} & 1 & 2 & 3 & 4 \\\\ \mathbf{2} & 2 & 4 & 6 & 8 \\\\
+ \mathbf{3} & 3 & 6 & 9 & 12 \end{array}$$
+
+There are 8 distinct terms {1, 2, 3, 4, 6, 8, 9, 12}, therefore $P(3, 4) = 8$.
+
+You are given that:
+
+$$\begin{align} & P(64, 64) = 1\\,263, \\\\
+ & P(12, 345) = 1\\,998, \text{ and} \\\\ & P(32, {10}^{15}) = 13\\,826\\,382\\,602\\,124\\,302. \\\\
+\end{align}$$
+
+Find $P(64, {10}^{16})$.
+
+# --hints--
+
+`multiplicationTable()` should return `258381958195474750`.
+
+```js
+assert.strictEqual(multiplicationTable(), 258381958195474750);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function multiplicationTable() {
+
+ return true;
+}
+
+multiplicationTable();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-467-superinteger.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-467-superinteger.md
new file mode 100644
index 00000000000..9b0caad1704
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-467-superinteger.md
@@ -0,0 +1,59 @@
+---
+id: 5900f5411000cf542c510052
+title: 'Problem 467: Superinteger'
+challengeType: 1
+forumTopicId: 302142
+dashedName: problem-467-superinteger
+---
+
+# --description--
+
+An integer $s$ is called a superinteger of another integer $n$ if the digits of $n$ form a subsequence of the digits of $s$.
+
+For example, 2718281828 is a superinteger of 18828, while 314159 is not a superinteger of 151.
+
+Let $p(n)$ be the $n$th prime number, and let $c(n)$ be the $n$th composite number. For example, $p(1) = 2$, $p(10) = 29$, $c(1) = 4$ and $c(10) = 18$.
+
+$$\begin{align} & \\{p(i) : i ≥ 1\\} = \\{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, \ldots \\} \\\\
+ & \\{c(i) : i ≥ 1\\} = \\{4, 6, 8, 9, 10, 12, 14, 15, 16, 18, \ldots \\} \end{align}$$
+
+Let $P^D$ the sequence of the digital roots of $\\{p(i)\\}$ ($C^D$ is defined similarly for $\\{c(i)\\}$):
+
+$$\begin{align} & P^D = \\{2, 3, 5, 7, 2, 4, 8, 1, 5, 2, \ldots \\} \\\\
+ & C^D = \\{4, 6, 8, 9, 1, 3, 5, 6, 7, 9, \ldots \\} \end{align}$$
+
+Let $P_n$ be the integer formed by concatenating the first $n$ elements of $P^D$ ($C_n$ is defined similarly for $C^D$).
+
+$$\begin{align} & P_{10} = 2\\,357\\,248\\,152 \\\\
+ & C_{10} = 4\\,689\\,135\\,679 \end{align}$$
+
+Let $f(n)$ be the smallest positive integer that is a common superinteger of $P_n$ and $C_n$. For example, $f(10) = 2\\,357\\,246\\,891\\,352\\,679$, and $f(100)\bmod 1\\,000\\,000\\,007 = 771\\,661\\,825$.
+
+Find $f(10\\,000)\bmod 1\\,000\\,000\\,007$.
+
+# --hints--
+
+`superinteger()` should return `775181359`.
+
+```js
+assert.strictEqual(superinteger(), 775181359);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function superinteger() {
+
+ return true;
+}
+
+superinteger();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-468-smooth-divisors-of-binomial-coefficients.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-468-smooth-divisors-of-binomial-coefficients.md
new file mode 100644
index 00000000000..dbd4119b933
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-468-smooth-divisors-of-binomial-coefficients.md
@@ -0,0 +1,54 @@
+---
+id: 5900f5411000cf542c510054
+title: 'Problem 468: Smooth divisors of binomial coefficients'
+challengeType: 1
+forumTopicId: 302143
+dashedName: problem-468-smooth-divisors-of-binomial-coefficients
+---
+
+# --description--
+
+An integer is called B-smooth if none of its prime factors is greater than $B$.
+
+Let $SB(n)$ be the largest B-smooth divisor of $n$.
+
+Examples:
+
+$$\begin{align} & S_1(10) = 1 \\\\
+ & S_4(2\\,100) = 12 \\\\ & S_{17}(2\\,496\\,144) = 5\\,712 \end{align}$$
+
+Define $F(n) = \displaystyle\sum_{B = 1}^n \sum_{r = 0}^n S_B(\displaystyle\binom{n}{r})$. Here, $\displaystyle\binom{n}{r}$ denotes the binomial coefficient.
+
+Examples:
+
+$$\begin{align} & F(11) = 3132 \\\\
+ & F(1\\,111)\bmod 1\\,000\\,000\\,993 = 706\\,036\\,312 \\\\ & F(111\\,111)\bmod 1\\,000\\,000\\,993 = 22\\,156\\,169 \end{align}$$
+
+Find $F(11\\,111\\,111)\bmod 1\\,000\\,000\\,993$.
+
+# --hints--
+
+`smoothDivisorsOfBinomialCoefficients()` should return `852950321`.
+
+```js
+assert.strictEqual(smoothDivisorsOfBinomialCoefficients(), 852950321);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function smoothDivisorsOfBinomialCoefficients() {
+
+ return true;
+}
+
+smoothDivisorsOfBinomialCoefficients();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-469-empty-chairs.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-469-empty-chairs.md
new file mode 100644
index 00000000000..3dce49fdd9a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-469-empty-chairs.md
@@ -0,0 +1,48 @@
+---
+id: 5900f5411000cf542c510053
+title: 'Problem 469: Empty chairs'
+challengeType: 1
+forumTopicId: 302144
+dashedName: problem-469-empty-chairs
+---
+
+# --description--
+
+In a room $N$ chairs are placed around a round table.
+
+Knights enter the room one by one and choose at random an available empty chair.
+
+To have enough elbow room the knights always leave at least one empty chair between each other.
+
+When there aren't any suitable chairs left, the fraction $C$ of empty chairs is determined. We also define $E(N)$ as the expected value of $C$.
+
+We can verify that $E(4) = \frac{1}{2}$ and $E(6) = \frac{5}{9}$.
+
+Find $E({10}^{18})$. Give your answer rounded to fourteen decimal places in the form 0.abcdefghijklmn.
+
+# --hints--
+
+`emptyChairs()` should return `0.56766764161831`.
+
+```js
+assert.strictEqual(emptyChairs(), 0.56766764161831);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function emptyChairs() {
+
+ return true;
+}
+
+emptyChairs();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-470-super-ramvok.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-470-super-ramvok.md
new file mode 100644
index 00000000000..7d0f1aad0ee
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-470-super-ramvok.md
@@ -0,0 +1,50 @@
+---
+id: 5900f5431000cf542c510055
+title: 'Problem 470: Super Ramvok'
+challengeType: 1
+forumTopicId: 302146
+dashedName: problem-470-super-ramvok
+---
+
+# --description--
+
+Consider a single game of Ramvok:
+
+Let $t$ represent the maximum number of turns the game lasts. If $t = 0$, then the game ends immediately. Otherwise, on each turn $i$, the player rolls a die. After rolling, if $i < t$ the player can either stop the game and receive a prize equal to the value of the current roll, or discard the roll and try again next turn. If $i = t$, then the roll cannot be discarded and the prize must be accepted. Before the game begins, $t$ is chosen by the player, who must then pay an up-front cost $ct$ for some constant $c$. For $c = 0$, $t$ can be chosen to be infinite (with an up-front cost of 0). Let $R(d, c)$ be the expected profit (i.e. net gain) that the player receives from a single game of optimally-played Ramvok, given a fair $d$-sided die and cost constant $c$. For example, $R(4, 0.2) = 2.65$. Assume that the player has sufficient funds for paying any/all up-front costs.
+
+Now consider a game of Super Ramvok:
+
+In Super Ramvok, the game of Ramvok is played repeatedly, but with a slight modification. After each game, the die is altered. The alteration process is as follows: The die is rolled once, and if the resulting face has its pips visible, then that face is altered to be blank instead. If the face is already blank, then it is changed back to its original value. After the alteration is made, another game of Ramvok can begin (and during such a game, at each turn, the die is rolled until a face with a value on it appears). The player knows which faces are blank and which are not at all times. The game of Super Ramvok ends once all faces of the die are blank.
+
+Let $S(d, c)$ be the expected profit that the player receives from an optimally-played game of Super Ramvok, given a fair $d$-sided die to start (with all sides visible), and cost constant $c$. For example, $S(6, 1) = 208.3$.
+
+Let $F(n) = \sum_{4 ≤ d ≤ n} \sum_{0 ≤ c ≤ n} S(d, c)$.
+
+Calculate $F(20)$, rounded to the nearest integer.
+
+# --hints--
+
+`superRamvok()` should return `147668794`.
+
+```js
+assert.strictEqual(superRamvok(), 147668794);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function superRamvok() {
+
+ return true;
+}
+
+superRamvok();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-471-triangle-inscribed-in-ellipse.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-471-triangle-inscribed-in-ellipse.md
new file mode 100644
index 00000000000..87fba0ff50a
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-471-triangle-inscribed-in-ellipse.md
@@ -0,0 +1,60 @@
+---
+id: 5900f5431000cf542c510056
+title: 'Problem 471: Triangle inscribed in ellipse'
+challengeType: 1
+forumTopicId: 302148
+dashedName: problem-471-triangle-inscribed-in-ellipse
+---
+
+# --description--
+
+The triangle $ΔABC$ is inscribed in an ellipse with equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, $0 < 2b < a$, $a$ and $b$ integers.
+
+Let $r(a, b)$ be the radius of the incircle of $ΔABC$ when the incircle has center $(2b, 0)$ and $A$ has coordinates $\left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right)$.
+
+For example, $r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2$.
+
+
+
+
+
+Let $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
+
+You are given $G(10) = 20.59722222$, $G(100) = 19223.60980$ (rounded to 10 significant digits).
+
+Find $G({10}^{11})$. Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent.
+
+For $G(10)$ the answer would have been `2.059722222e1`
+
+# --hints--
+
+`triangleInscribedInEllipse()` should return a string.
+
+```js
+assert(typeof triangleInscribedInEllipse() === 'string');
+```
+
+`triangleInscribedInEllipse()` should return the string `1.895093981e31`.
+
+```js
+assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function triangleInscribedInEllipse() {
+
+ return true;
+}
+
+triangleInscribedInEllipse();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-472-comfortable-distance-ii.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-472-comfortable-distance-ii.md
new file mode 100644
index 00000000000..25c9c601cf6
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-472-comfortable-distance-ii.md
@@ -0,0 +1,56 @@
+---
+id: 5900f5451000cf542c510057
+title: 'Problem 472: Comfortable Distance II'
+challengeType: 1
+forumTopicId: 302149
+dashedName: problem-472-comfortable-distance-ii
+---
+
+# --description--
+
+There are $N$ seats in a row. $N$ people come one after another to fill the seats according to the following rules:
+
+1. No person sits beside another.
+1. The first person chooses any seat.
+1. Each subsequent person chooses the seat furthest from anyone else already seated, as long as it does not violate rule 1. If there is more than one choice satisfying this condition, then the person chooses the leftmost choice.
+
+Note that due to rule 1, some seats will surely be left unoccupied, and the maximum number of people that can be seated is less than $N$ (for $N > 1$).
+
+Here are the possible seating arrangements for $N = 15$:
+
+
+
+We see that if the first person chooses correctly, the 15 seats can seat up to 7 people. We can also see that the first person has 9 choices to maximize the number of people that may be seated.
+
+Let $f(N)$ be the number of choices the first person has to maximize the number of occupants for $N$ seats in a row. Thus, $f(1) = 1$, $f(15) = 9$, $f(20) = 6$, and $f(500) = 16$.
+
+Also, $\sum f(N) = 83$ for $1 ≤ N ≤ 20$ and $\sum f(N) = 13\\,343$ for $1 ≤ N ≤ 500$.
+
+Find $\sum f(N)$ for $1 ≤ N ≤ {10}^{12}$. Give the last 8 digits of your answer.
+
+# --hints--
+
+`comfortableDistanceTwo()` should return `73811586`.
+
+```js
+assert.strictEqual(comfortableDistanceTwo(), 73811586);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function comfortableDistanceTwo() {
+
+ return true;
+}
+
+comfortableDistanceTwo();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-473-phigital-number-base.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-473-phigital-number-base.md
new file mode 100644
index 00000000000..97a545fed4c
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-473-phigital-number-base.md
@@ -0,0 +1,56 @@
+---
+id: 5900f5461000cf542c510058
+title: 'Problem 473: Phigital number base'
+challengeType: 1
+forumTopicId: 302150
+dashedName: problem-473-phigital-number-base
+---
+
+# --description--
+
+Let $\varphi$ be the golden ratio: $\varphi = \frac{1+\sqrt{5}}{2}.$
+
+Remarkably it is possible to write every positive integer as a sum of powers of $\varphi$ even if we require that every power of $\varphi$ is used at most once in this sum.
+
+Even then this representation is not unique.
+
+We can make it unique by requiring that no powers with consecutive exponents are used and that the representation is finite.
+
+E.g:
+
+$2 = \varphi + \varphi^{-2}$ and $3 = \varphi^{2} + \varphi^{-2}$
+
+To represent this sum of powers of $\varphi$ we use a string of 0's and 1's with a point to indicate where the negative exponents start. We call this the representation in the phigital numberbase.
+
+So $1 = 1_{\varphi}$, $2 = 10.01_{\varphi}$, $3 = 100.01_{\varphi}$ and $14 = 100100.001001_{\varphi}$. The strings representing 1, 2 and 14 in the phigital number base are palindromic, while the string representing 3 is not (the phigital point is not the middle character).
+
+The sum of the positive integers not exceeding 1000 whose phigital representation is palindromic is 4345.
+
+Find the sum of the positive integers not exceeding $10^{10}$ whose phigital representation is palindromic.
+
+# --hints--
+
+`phigitalNumberBase()` should return `35856681704365`.
+
+```js
+assert.strictEqual(phigitalNumberBase(), 35856681704365);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function phigitalNumberBase() {
+
+ return true;
+}
+
+phigitalNumberBase();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-474-last-digits-of-divisors.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-474-last-digits-of-divisors.md
new file mode 100644
index 00000000000..e63a971d336
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-474-last-digits-of-divisors.md
@@ -0,0 +1,44 @@
+---
+id: 5900f5471000cf542c510059
+title: 'Problem 474: Last digits of divisors'
+challengeType: 1
+forumTopicId: 302151
+dashedName: problem-474-last-digits-of-divisors
+---
+
+# --description--
+
+For a positive integer $n$ and digits $d$, we define $F(n, d)$ as the number of the divisors of $n$ whose last digits equal $d$.
+
+For example, $F(84, 4) = 3$. Among the divisors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), three of them (4, 14, 84) have the last digit 4.
+
+We can also verify that $F(12!, 12) = 11$ and $F(50!, 123) = 17\\,888$.
+
+Find $F({10}^6!, 65\\,432) \text{ modulo } ({10}^{16} + 61)$.
+
+# --hints--
+
+`lastDigitsOfDivisors()` should return `9690646731515010`.
+
+```js
+assert.strictEqual(lastDigitsOfDivisors(), 9690646731515010);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function lastDigitsOfDivisors() {
+
+ return true;
+}
+
+lastDigitsOfDivisors();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-475-music-festival.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-475-music-festival.md
new file mode 100644
index 00000000000..9f019e969d0
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-475-music-festival.md
@@ -0,0 +1,48 @@
+---
+id: 5900f5481000cf542c51005a
+title: 'Problem 475: Music festival'
+challengeType: 1
+forumTopicId: 302152
+dashedName: problem-475-music-festival
+---
+
+# --description--
+
+$12n$ musicians participate at a music festival. On the first day, they form $3n$ quartets and practice all day.
+
+It is a disaster. At the end of the day, all musicians decide they will never again agree to play with any member of their quartet.
+
+On the second day, they form $4n$ trios, each musician avoiding his previous quartet partners.
+
+Let $f(12n)$ be the number of ways to organize the trios amongst the $12n$ musicians.
+
+You are given $f(12) = 576$ and $f(24)\bmod 1\\,000\\,000\\,007 = 509\\,089\\,824$.
+
+Find $f(600)\bmod 1\\,000\\,000\\,007$.
+
+# --hints--
+
+`musicFestival()` should return `75780067`.
+
+```js
+assert.strictEqual(musicFestival(), 75780067);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function musicFestival() {
+
+ return true;
+}
+
+musicFestival();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-476-circle-packing-ii.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-476-circle-packing-ii.md
new file mode 100644
index 00000000000..c6f88e38013
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-476-circle-packing-ii.md
@@ -0,0 +1,44 @@
+---
+id: 5900f5481000cf542c51005b
+title: 'Problem 476: Circle Packing II'
+challengeType: 1
+forumTopicId: 302153
+dashedName: problem-476-circle-packing-ii
+---
+
+# --description--
+
+Let $R(a, b, c)$ be the maximum area covered by three non-overlapping circles inside a triangle with edge lengths $a$, $b$ and $c$.
+
+Let $S(n)$ be the average value of $R(a, b, c)$ over all integer triplets $(a, b, c)$ such that $1 ≤ a ≤ b ≤ c < a + b ≤ n$.
+
+You are given $S(2) = R(1, 1, 1) ≈ 0.31998$, $S(5) ≈ 1.25899$.
+
+Find $S(1803)$ rounded to 5 decimal places behind the decimal point.
+
+# --hints--
+
+`circlePackingTwo()` should return `110242.87794`.
+
+```js
+assert.strictEqual(circlePackingTwo(), 110242.87794);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function circlePackingTwo() {
+
+ return true;
+}
+
+circlePackingTwo();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-477-number-sequence-game.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-477-number-sequence-game.md
new file mode 100644
index 00000000000..18bcc8e538b
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-477-number-sequence-game.md
@@ -0,0 +1,62 @@
+---
+id: 5900f54a1000cf542c51005c
+title: 'Problem 477: Number Sequence Game'
+challengeType: 1
+forumTopicId: 302154
+dashedName: problem-477-number-sequence-game
+---
+
+# --description--
+
+The number sequence game starts with a sequence $S$ of $N$ numbers written on a line.
+
+Two players alternate turns. At his turn, a player must select and remove either the first or the last number remaining in the sequence.
+
+The player score is the sum of all the numbers he has taken. Each player attempts to maximize his own sum.
+
+If $N = 4$ and $S = \\{1, 2, 10, 3\\}$, then each player maximizes his score as follows:
+
+- Player 1: removes the first number (1)
+- Player 2: removes the last number from the remaining sequence (3)
+- Player 1: removes the last number from the remaining sequence (10)
+- Player 2: removes the remaining number (2)
+
+Player 1 score is $1 + 10 = 11$.
+
+Let $F(N)$ be the score of player 1 if both players follow the optimal strategy for the sequence $S = \\{s_1, s_2, \ldots, s_N\\}$ defined as:
+
+- $s_1 = 0$
+- $s_{i + 1} = ({s_i}^2 + 45)$ modulo $1\\,000\\,000\\,007$
+
+The sequence begins with $S = \\{0, 45, 2\\,070, 4\\,284\\,945, 753\\,524\\,550, 478\\,107\\,844, 894\\,218\\,625, \ldots\\}$.
+
+You are given $F(2) = 45$, $F(4) = 4\\,284\\,990$, $F(100) = 26\\,365\\,463\\,243$, $F(104) = 2\\,495\\,838\\,522\\,951$.
+
+Find $F({10}^8)$.
+
+# --hints--
+
+`numberSequenceGame()` should return `25044905874565164`.
+
+```js
+assert.strictEqual(numberSequenceGame(), 25044905874565164);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function numberSequenceGame() {
+
+ return true;
+}
+
+numberSequenceGame();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-478-mixtures.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-478-mixtures.md
new file mode 100644
index 00000000000..d2f0dbd2054
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-478-mixtures.md
@@ -0,0 +1,56 @@
+---
+id: 5900f54c1000cf542c51005e
+title: 'Problem 478: Mixtures'
+challengeType: 1
+forumTopicId: 302155
+dashedName: problem-478-mixtures
+---
+
+# --description--
+
+Let us consider mixtures of three substances: $A$, $B$ and $C$. A mixture can be described by a ratio of the amounts of $A$, $B$, and $C$ in it, i.e., $(a : b : c)$. For example, a mixture described by the ratio (2 : 3 : 5) contains 20% $A$, 30% $B$ and 50% $C$.
+
+For the purposes of this problem, we cannot separate the individual components from a mixture. However, we can combine different amounts of different mixtures to form mixtures with new ratios.
+
+For example, say we have three mixtures with ratios (3 : 0 : 2), (3 : 6 : 11) and (3 : 3 : 4). By mixing 10 units of the first, 20 units of the second and 30 units of the third, we get a new mixture with ratio (6 : 5 : 9), since: ($10 \times \frac{3}{5} + 20 \times \frac{3}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{0}{5} + 20 \times \frac{6}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{2}{5} + 20 \times \frac{11}{20} + 30 \times \frac{4}{10}$) = (18 : 15 : 27) = (6 : 5 : 9)
+
+However, with the same three mixtures, it is impossible to form the ratio (3 : 2 : 1), since the amount of $B$ is always less than the amount of $C$.
+
+Let $n$ be a positive integer. Suppose that for every triple of integers $(a, b, c)$ with $0 ≤ a, b, c ≤ n$ and $gcd(a, b, c) = 1$, we have a mixture with ratio $(a : b : c)$. Let $M(n)$ be the set of all such mixtures.
+
+For example, $M(2)$ contains the 19 mixtures with the following ratios:
+
+{(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
+
+Let $E(n)$ be the number of subsets of $M(n)$ which can produce the mixture with ratio (1 : 1 : 1), i.e., the mixture with equal parts $A$, $B$ and $C$.
+
+We can verify that $E(1) = 103$, $E(2) = 520\\,447$, $E(10)\bmod {11}^8 = 82\\,608\\,406$ and $E(500)\bmod {11}^8 = 13\\,801\\,403$.
+
+Find $E(10\\,000\\,000)\bmod {11}^8$.
+
+# --hints--
+
+`mixtures()` should return `59510340`.
+
+```js
+assert.strictEqual(mixtures(), 59510340);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function mixtures() {
+
+ return true;
+}
+
+mixtures();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-479-roots-on-the-rise.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-479-roots-on-the-rise.md
new file mode 100644
index 00000000000..b905a648468
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-479-roots-on-the-rise.md
@@ -0,0 +1,46 @@
+---
+id: 5900f54b1000cf542c51005d
+title: 'Problem 479: Roots on the Rise'
+challengeType: 1
+forumTopicId: 302156
+dashedName: problem-479-roots-on-the-rise
+---
+
+# --description--
+
+Let $a_k$, $b_k$, and $c_k$ represent the three solutions (real or complex numbers) to the expression $\frac{1}{x} = {\left(\frac{k}{x} \right)}^2 (k + x^2) - kx$.
+
+For instance, for $k = 5$, we see that $\\{a_5, b_5, c_5\\}$ is approximately $\\{5.727244, -0.363622 + 2.057397i, -0.363622 - 2.057397i\\}$.
+
+Let $S(n) = \displaystyle\sum_{p = 1}^n \sum_{k = 1}^n {(a_k + b_k)}^p {(b_k + c_k)}^p {(c_k + a_k)}^p$ for all integers $p$, $k$ such that $1 ≤ p, k ≤ n$.
+
+Interestingly, $S(n)$ is always an integer. For example, $S(4) = 51\\,160$.
+
+Find $S({10}^6) \text{ modulo } 1\\,000\\,000\\,007$.
+
+# --hints--
+
+`rootsOnTheRise()` should return `191541795`.
+
+```js
+assert.strictEqual(rootsOnTheRise(), 191541795);
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function rootsOnTheRise() {
+
+ return true;
+}
+
+rootsOnTheRise();
+```
+
+# --solutions--
+
+```js
+// solution required
+```
diff --git a/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-480-the-last-question.md b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-480-the-last-question.md
new file mode 100644
index 00000000000..b07b59bb692
--- /dev/null
+++ b/curriculum/challenges/ukrainian/18-project-euler/project-euler-problems-401-to-480/problem-480-the-last-question.md
@@ -0,0 +1,82 @@
+---
+id: 5900f54c1000cf542c51005f
+title: 'Problem 480: The Last Question'
+challengeType: 1
+forumTopicId: 302158
+dashedName: problem-480-the-last-question
+---
+
+# --description--
+
+Consider all the words which can be formed by selecting letters, in any order, from the phrase:
+
+$$\mathbf{\text{thereisasyetinsufficientdataforameaningfulanswer}}$$
+
+Suppose those with 15 letters or less are listed in alphabetical order and numbered sequentially starting at 1.
+
+The list would include:
+
+$$\begin{align} & 1: \text{a} \\\\
+ & 2: \text{aa} \\\\ & 3: \text{aaa} \\\\
+ & 4: \text{aaaa} \\\\ & 5: \text{aaaaa} \\\\
+ & 6: \text{aaaaaa} \\\\ & 7: \text{aaaaaac} \\\\
+ & 8: \text{aaaaaacd} \\\\ & 9: \text{aaaaaacde} \\\\
+ & 10: \text{aaaaaacdee} \\\\ & 11: \text{aaaaaacdeee} \\\\
+ & 12: \text{aaaaaacdeeee} \\\\ & 13: \text{aaaaaacdeeeee} \\\\
+ & 14: \text{aaaaaacdeeeeee} \\\\ & 15: \text{aaaaaacdeeeeeef} \\\\
+ & 16: \text{aaaaaacdeeeeeeg} \\\\ & 17: \text{aaaaaacdeeeeeeh} \\\\
+ & \ldots \\\\ & 28: \text{aaaaaacdeeeeeey} \\\\
+ & 29: \text{aaaaaacdeeeeef} \\\\ & 30: \text{aaaaaacdeeeeefe} \\\\
+ & \ldots \\\\ & 115246685191495242: \text{euleoywuttttsss} \\\\
+ & 115246685191495243: \text{euler} \\\\ & 115246685191495244: \text{eulera} \\\\
+ & ... \\\\ & 525069350231428029: \text{ywuuttttssssrrr} \\\\
+\end{align}$$
+
+Define $P(w)$ as the position of the word $w$.
+
+Define $W(p)$ as the word in position $p$.
+
+We can see that $P(w)$ and $W(p)$ are inverses: $P(W(p)) = p$ and $W(P(w)) = w$.
+
+Examples:
+
+$$\begin{align} & W(10) = \text{ aaaaaacdee} \\\\
+ & P(\text{aaaaaacdee}) = 10 \\\\ & W(115246685191495243) = \text{ euler} \\\\
+ & P(\text{euler}) = 115246685191495243 \\\\ \end{align}$$
+
+Find $$W(P(\text{legionary}) + P(\text{calorimeters}) - P(\text{annihilate}) + P(\text{orchestrated}) - P(\text{fluttering})).$$
+
+Give your answer using lowercase characters (no punctuation or space).
+
+# --hints--
+
+`euler480()` should return a string.
+
+```js
+assert(typeof euler480() === 'string');
+```
+
+`euler480()` should return the string `turnthestarson`.
+
+```js
+assert.strictEqual(euler480(), 'turnthestarson');
+```
+
+# --seed--
+
+## --seed-contents--
+
+```js
+function euler480() {
+
+ return true;
+}
+
+euler480();
+```
+
+# --solutions--
+
+```js
+// solution required
+```