---
id: 5900f48b1000cf542c50ff9e
title: 'Problem 287: Quadtree-Kodierung (ein einfacher Kompressionsalgorithmus)'
challengeType: 1
forumTopicId: 301938
dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
---
# --description--
Die Quadtree-Kodierung ermöglicht es uns, ein $2^N×2^N$-Schwarzweißbild als eine Folge von Bits (0 und 1) zu beschreiben. Diese Sequenzen sind von links nach rechts wie folgt zu lesen:
- der erste Teil betrifft die gesamte Region $2^N×2^N$;
- "0" bedeutet eine Aufteilung:
- die aktuelle Region $2^n×2^n$ wird in 4 Unterregionen der Dimension $2^{n - 1}×2^{n - 1}$ unterteilt,
- die nächsten Bits enthalten die Beschreibung der Unterregionen oben links, oben rechts, unten links und unten rechts - in dieser Reihenfolge;
- "10" gibt an, dass die aktuelle Region nur schwarze Pixel enthält;
- "11" gibt an, dass die aktuelle Region nur weiße Pixel enthält.
Betrachte das folgende 4×4-Bild (farbige Markierungen kennzeichnen die Stellen, an denen eine Teilung auftreten kann):
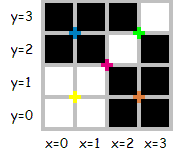 Dieses Bild kann durch mehrere Folgen beschrieben werden, zum Beispiel: "001010101001011111011010101010", der Länge 30, oder "0100101111101110", der Länge 16, welches die minimale Folge für dieses Bild ist.
Für einen positven Integer $N$ definiere $D_N$ als das $2^N×2^N$-Bild mit dem folgenden Färbungsschema:
- pixel mit den Koordinaten $x = 0$, $y = 0$ entspricht dem unteren linken Pixel,
- wenn ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$, dann ist das Pixel schwarz,
- andernfalls ist das Pixel weiß.
Was ist die Länge der minimalen Sequentz, die $D_{24} $ beschreibt?
# --hints--
`quadtreeEncoding()` sollte `313135496` zurückgeben.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
Dieses Bild kann durch mehrere Folgen beschrieben werden, zum Beispiel: "001010101001011111011010101010", der Länge 30, oder "0100101111101110", der Länge 16, welches die minimale Folge für dieses Bild ist.
Für einen positven Integer $N$ definiere $D_N$ als das $2^N×2^N$-Bild mit dem folgenden Färbungsschema:
- pixel mit den Koordinaten $x = 0$, $y = 0$ entspricht dem unteren linken Pixel,
- wenn ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$, dann ist das Pixel schwarz,
- andernfalls ist das Pixel weiß.
Was ist die Länge der minimalen Sequentz, die $D_{24} $ beschreibt?
# --hints--
`quadtreeEncoding()` sollte `313135496` zurückgeben.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
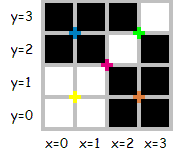 Dieses Bild kann durch mehrere Folgen beschrieben werden, zum Beispiel: "001010101001011111011010101010", der Länge 30, oder "0100101111101110", der Länge 16, welches die minimale Folge für dieses Bild ist.
Für einen positven Integer $N$ definiere $D_N$ als das $2^N×2^N$-Bild mit dem folgenden Färbungsschema:
- pixel mit den Koordinaten $x = 0$, $y = 0$ entspricht dem unteren linken Pixel,
- wenn ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$, dann ist das Pixel schwarz,
- andernfalls ist das Pixel weiß.
Was ist die Länge der minimalen Sequentz, die $D_{24} $ beschreibt?
# --hints--
`quadtreeEncoding()` sollte `313135496` zurückgeben.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
Dieses Bild kann durch mehrere Folgen beschrieben werden, zum Beispiel: "001010101001011111011010101010", der Länge 30, oder "0100101111101110", der Länge 16, welches die minimale Folge für dieses Bild ist.
Für einen positven Integer $N$ definiere $D_N$ als das $2^N×2^N$-Bild mit dem folgenden Färbungsschema:
- pixel mit den Koordinaten $x = 0$, $y = 0$ entspricht dem unteren linken Pixel,
- wenn ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$, dann ist das Pixel schwarz,
- andernfalls ist das Pixel weiß.
Was ist die Länge der minimalen Sequentz, die $D_{24} $ beschreibt?
# --hints--
`quadtreeEncoding()` sollte `313135496` zurückgeben.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```