freeCodeCamp/curriculum/challenges/german/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f3ec1000cf542c50feff	Problem 128: Hexagonal tile differences	1	301755	problem-128-hexagonal-tile-differences

--description--

A hexagonal tile with number 1 is surrounded by a ring of six hexagonal tiles, starting at "12 o'clock" and numbering the tiles 2 to 7 in an anti-clockwise direction.

Neue Ringe werden auf die gleiche Weise hinzugefügt, wobei die nächsten Ringe die Nummern 8 bis 19, 20 bis 37, 38 bis 61 usw. tragen. Das folgende Diagramm zeigt die ersten drei Ringe.

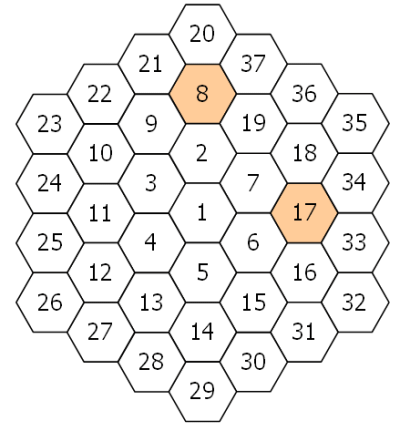
By finding the difference between tile n and each of its six neighbours we shall define PD(n) to be the number of those differences which are prime.

For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. Somit ist PD(8) = 3.

In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence PD(17) = 2.

Es kann gezeigt werden, dass der Maximalwert von PD(n) $ 3 ist.

If all of the tiles for which PD(n) = 3 are listed in ascending order to form a sequence, the 10th tile would be 271.

Find the 2000th tile in this sequence.

--hints--

hexagonalTile(10) sollte 271 zurückgeben.

assert.strictEqual(hexagonalTile(10), 271);

hexagonalTile(2000) sollte 14516824220 zurückgeben.

assert.strictEqual(hexagonalTile(2000), 14516824220);

--seed--

--seed-contents--

function hexagonalTile(tileIndex) {

  return true;
}

hexagonalTile(10);

--solutions--

class PrimeSeive {
  constructor(num) {
    const seive = Array(Math.floor((num - 1) / 2)).fill(true);
    const upper = Math.floor((num - 1) / 2);
    const sqrtUpper = Math.floor((Math.sqrt(num) - 1) / 2);

    for (let i = 0; i <= sqrtUpper; i++) {
      if (seive[i]) {
        // Mark value in seive array
        const prime = 2 * i + 3;
        // Mark all multiples of this number as false (not prime)
        const primeSqaredIndex = 2 * i ** 2 + 6 * i + 3;
        for (let j = primeSqaredIndex; j < upper; j += prime) {
          seive[j] = false;
        }
      }
    }

    this._seive = seive;
  }

  isPrime(num) {
    return num === 2
      ? true
      : num % 2 === 0
        ? false
        : this.isOddPrime(num);
  }

  isOddPrime(num) {
    return this._seive[(num - 3) / 2];
  }
};

function hexagonalTile(tileIndex) {
  const primeSeive = new PrimeSeive(tileIndex * 420);
  let count = 1;
  let n = 1;
  let number = 0;

  while (count < tileIndex) {
    if (primeSeive.isPrime(6*n - 1) &&
        primeSeive.isPrime(6*n + 1) &&
        primeSeive.isPrime(12*n + 5)) {
      number = 3*n*n - 3*n + 2;
      count++;
      if (count >= tileIndex) break;
    }
    if (primeSeive.isPrime(6*n + 5) &&
        primeSeive.isPrime(6*n - 1) &&
        primeSeive.isPrime(12*n - 7) && n != 1) {
      number = 3*n*n + 3*n + 1;
      count++;
    }
    n++;
  }
  return number;
}