freeCodeCamp/curriculum/challenges/german/10-coding-interview-prep/project-euler/problem-257-angular-bisectors.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f46e1000cf542c50ff80	Problem 257: Angular Bisectors	1	301905	problem-257-angular-bisectors

--description--

Given is an integer sided triangle ABC with sides a ≤ b ≤ c (AB = c, BC = a and AC = b).

The angular bisectors of the triangle intersect the sides at points E, F and G (see picture below).

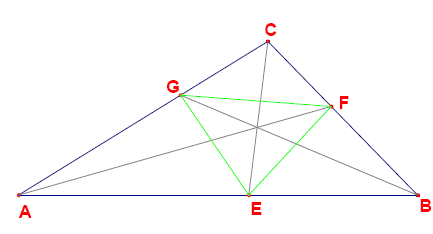
The segments EF, EG and FG partition the triangle ABC into four smaller triangles: AEG, BFE, CGF and EFG. It can be proven that for each of these four triangles the ratio \frac{\text{area}(ABC)}{\text{area}(\text{subtriangle})} is rational. However, there exist triangles for which some or all of these ratios are integral.

How many triangles ABC with perimeter ≤ 100\\,000\\,000 exist so that the ratio \frac{\text{area}(ABC)}{\text{area}(AEG)} is integral?

--hints--

angularBisectors() should return 139012411.

assert.strictEqual(angularBisectors(), 139012411);

--seed--

--seed-contents--

function angularBisectors() {

  return true;
}

angularBisectors();

--solutions--

// solution required