freeCodeCamp/curriculum/challenges/german/10-coding-interview-prep/project-euler/problem-199-iterative-circle-packing.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4341000cf542c50ff46	Problem 199: Iterative Kreise	1	301837	problem-199-iterative-circle-packing

--description--

Drei Kreise mit gleichem Radius werden innerhalb eines größeren Kreises so angeordnet, dass jedes Kreispaar tangiert wird und sich die inneren Kreise nicht überschneiden. Es gibt vier unbedeckte "Lücken", die iterativ mit weiteren Kreistangenten gefüllt werden sollen.

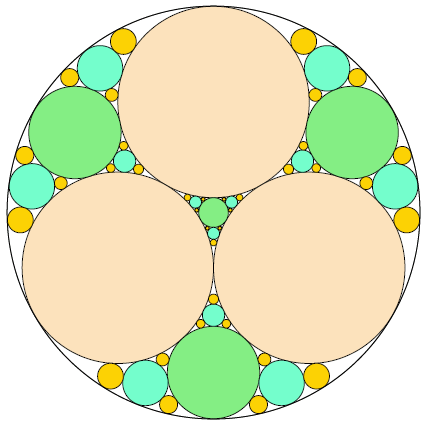
Bei jeder Iteration wird ein maximal großer Kreis in jede Lücke gesetzt, wodurch weitere Lücken für die nächste Iteration entstehen. Nach 3 Iterationen (siehe Bild) gibt es 108 Lücken und der Anteil der Fläche, die nicht von Kreisen bedeckt ist, beträgt 0,06790342, gerundet auf acht Dezimalstellen.

Welcher Anteil der Fläche ist nach n Iterationen nicht von Kreisen bedeckt? Gib deine Antwort auf acht Dezimalstellen gerundet im Format x.xxxxxxxx an.

--hints--

iterativeCirclePacking(10) sollte eine Zahl zurückgeben.

assert(typeof iterativeCirclePacking(10) === 'number');

iterativeCirclePacking(10) sollte 0.00396087 zurückgeben.

assert.strictEqual(iterativeCirclePacking(10), 0.00396087);

iterativeCirclePacking(3) sollte 0.06790342 zurückgeben.

assert.strictEqual(iterativeCirclePacking(3), 0.06790342);

--seed--

--seed-contents--

function iterativeCirclePacking(n) {

  return true;
}

iterativeCirclePacking(10);

--solutions--

function iterativeCirclePacking(n) {
  let k1 = 1;
  let k0 = k1 * (3 - 2 * Math.sqrt(3));
  let a0 = 1 / (k0 * k0);
  let a1 = 3 / (k1 * k1);
  a1 += 3 * getArea(k0, k1, k1, n);
  a1 += getArea(k1, k1, k1, n);
  let final = ((a0 - a1) / a0).toFixed(8);

  return parseFloat(final);
  function getArea(k1, k2, k3, depth) {
      if (depth == 0) return 0.0;
      let k4 = k1 + k2 + k3 + 2 * Math.sqrt(k1 * k2 + k2 * k3 + k3 * k1);
      let a = 1 / (k4 * k4);
      a += getArea(k1, k2, k4, depth - 1);
      a += getArea(k2, k3, k4, depth - 1);
      a += getArea(k3, k1, k4, depth - 1);
      return a;
  }
}