1.6 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f48d1000cf542c50ffa0 | Problem 289: Eulersche Zyklen | 1 | 301940 | problem-289-eulerian-cycles |
--description--
Lasse C(x,y) einen Kreis sein, der durch die Punkte (x, y), (x, y + 1), (x + 1, y) und (x + 1, y + 1) geht.
Für positive ganze Zahlen m und n sei E(m,n) eine Konfiguration, die aus den m·n Kreisen besteht: { C(x,y): 0 ≤ x < m, 0 ≤ y < n, x und y sind ganze Zahlen }
Ein Eulerscher Zyklus auf E(m,n) ist ein geschlossener Pfad, der jeden Bogen genau einmal durchläuft. Auf E(m,n) sind viele solcher Pfade möglich, aber wir interessieren uns nur für solche, die sich nicht selbst kreuzen: Ein nicht sich selbst kreuzender Pfad berührt sich nur an Gitterpunkten, aber er kreuzt sich nie.
Die folgende Abbildung zeigt E(3,3) und ein Beispiel für einen Eulerschen nicht kreuzenden Pfad.
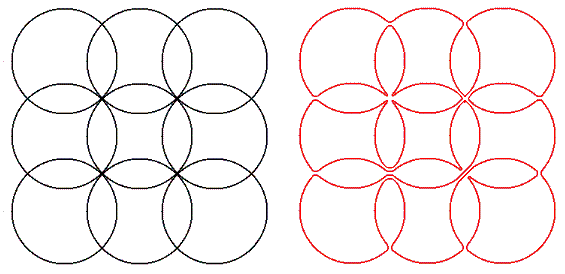
Lasse L(m,n) die Anzahl der Eulerschen sich nicht kreuzenden Pfade auf E(m,n) sein. Zum Beispiel ist L(1,2) = 2, L(2,2) = 37 und L(3,3) = 104290.
Finde L(6,10)\bmod {10}^{10}.
--hints--
eulerianCycles() sollte 6567944538 zurückgeben.
assert.strictEqual(eulerianCycles(), 6567944538);
--seed--
--seed-contents--
function eulerianCycles() {
return true;
}
eulerianCycles();
--solutions--
// solution required