2.0 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4b71000cf542c50ffca | Problem 331: Cross flips | 1 | 301989 | problem-331-cross-flips |
--description--
N×N Scheiben werden auf ein quadratisches Spielbrett gelegt. Jede Scheibe hat eine schwarze und eine weiße Seite.
In jedem Zug darf man sich eine Scheibe aussuchen und alle Scheiben umdrehen, die sich in der gleichen Zeile und Spalte wie diese Scheibe befinden: Es werden also 2 × N - 1 Scheiben umgedreht. Das Spiel endet, wenn von allen Scheiben die weisse Seite zu sehen ist. Das folgende Beispiel zeigt ein Spiel auf einem 5×5-Brett.
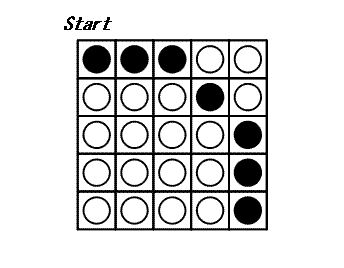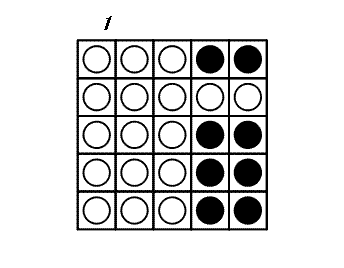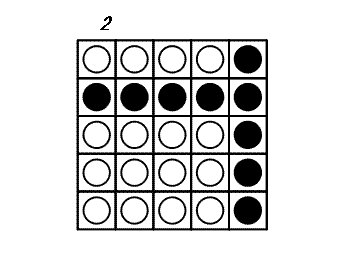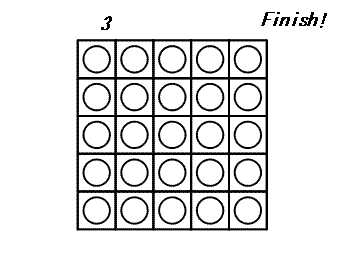
Es kann bewiesen werden, dass 3 die minimale Anzahl von Zügen ist, um dieses Spiel zu beenden.
Die untere linke Scheibe auf dem $N×N$-Brett hat die Koordinaten (0, 0); die untere rechte Scheibe hat die Koordinaten (N - 1,$0$) und die obere linke Scheibe hat die Koordinaten (0,$N - 1$).
Lasse C_N die folgende Konfiguration eines Brettes mit N × N Scheiben sein: Eine Scheibe bei (x, y), erfüllt die Bedingung N - 1 \le \sqrt{x^2 + y^2} \lt N, zeigt ihre schwarze Seite; andernfalls zeigt sie ihre weisse Seite. C_5 ist oben dargestellt.
Lasse T(N) die minimale Anzahl von Zügen sein, um ein Spiel ausgehend von der Konfiguration C_N zu beenden oder 0, wenn die Konfiguration C_N unlösbar ist. Wir haben gezeigt, dass T(5) = 3. Dir wird ebenfalls angegeben, dass T(10) = 29 und T(1\\,000) = 395\\,253.
Finde \displaystyle \sum_{i = 3}^{31} T(2^i - i).
--hints--
crossFlips() sollte 467178235146843500 zurückgeben.
assert.strictEqual(crossFlips(), 467178235146843500);
--seed--
--seed-contents--
function crossFlips() {
return true;
}
crossFlips();
--solutions--
// solution required