2.9 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f3db1000cf542c50feec | Problem 109: Dart | 1 | 301733 | problem-109-darts |
--description--
Beim Dartspiel wirft ein Spieler drei Darts auf eine Zielscheibe, die in zwanzig gleich große Abschnitte mit den Nummern eins bis zwanzig unterteilt ist.
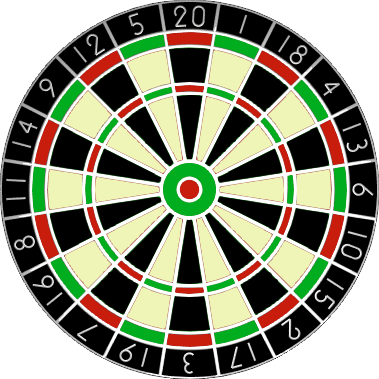
Die Punktzahl wird durch die Zahl des Bereich bestimmt, in dem der Dart landet. Eine Dart-Landung außerhalb des rot-grünen äußeren Rings wird mit Null bewertet. Die schwarzen und cremefarbenen Bereiche in diesem Ring stellen einfache Punkte dar. Der rot-grüne äußere und mittlere Ring erzielen jedoch doppelte bzw. dreifache Punkte.
Im Zentrum der Scheibe befinden sich zwei mittige Kreise, die Bullregion oder Bulls-eye genannt werden. Der äußere Bulle ist 25 Punkte wert und der innere Bulle ist ein Pasch, der 50 Punkte wert ist.
Es gibt viele Regelvariationen, aber bei dem beliebtesten Spiel beginnen die Spieler mit einer Punktzahl von 301 oder 501, und der erste Spieler, der seine laufende Punktzahl auf null bringt, ist der Gewinner. Es ist jedoch üblich, ein "Double Out"-System zu spielen, was bedeutet, dass der Spieler mit seinem letzten Dart ein Double (einschließlich des doppelten Bulls-Eye in der Mitte des Boards) treffen muss, um zu gewinnen; jeder andere Wurf, der seine laufende Gesamtpunktzahl auf eins oder weniger reduzieren würde, bedeutet, dass das Ergebnis für diesen Satz von drei Darts "Bust" ist.
Wenn ein Spieler in der Lage ist, seine aktuelle Punktzahl zu erreichen, wird dies als "Checkout" bezeichnet und das höchste Checkout ist 170: T20 T20 D25 (zwei dreifache 20er und doppelter Bulle). Bei einer Punktzahl von 6 gibt es genau elf verschiedene Möglichkeiten, zur Kasse zu gehen:
$$\begin{array} \text{D3} & & \\ D1 & D2 & \\ S2 & D2 & \\ D2 & D1 & \\ S4 & D1 & \\ S1 & S1 & D2 \\ S1 & T1 & D1 \\ S1 & S3 & D1 \\ D1 & D1 & D1 \\ D1 & S2 & D1 \\ S2 & S2 & D1 \end{array}$$
Beachte, dass D1 D2 sich von D2 D1 unterscheidet, da sie auf unterschiedlichen Doppeln enden. Die Kombination S1 T1 D1 wird jedoch als gleichwertig mit T1 S1 D1 angesehen. Außerdem werden bei der Betrachtung von Kombinationen keine Fehlschüsse berücksichtigt; so ist beispielsweise D3 dasselbe wie 0 D3 und 0 0 D3. Unglaublich, dass es insgesamt 42336 verschiedene Möglichkeiten des Checkouts gibt. Auf wie viele verschiedene Arten kann ein Spieler mit einer Punktzahl von weniger als 100 auschecken?
--hints--
darts() sollte 38182 zurückgeben.
assert.strictEqual(darts(), 38182);
--seed--
--seed-contents--
function darts() {
return true;
}
darts();
--solutions--
// solution required