1.6 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f3ea1000cf542c50fefd | Problem 126: Quaderförmige Ebenen | 1 | 301753 | problem-126-cuboid-layers |
--description--
The minimum number of cubes to cover every visible face on a cuboid measuring 3 x 2 x 1 is twenty-two.
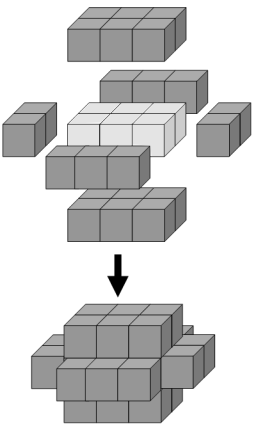
Fügen wir diesem Körper eine zweite Schicht hinzu, wären sechsundvierzig Würfel erforderlich, um jede sichtbare Fläche zu bedecken, für die dritte Schicht wären achtundsiebzig Würfel erforderlich, und für die vierte Schicht wären einhundertachtzehn Würfel erforderlich, um jede sichtbare Fläche zu bedecken.
Für die erste Schicht auf einem Quader mit den Maßen 5 x 1 x 1 werden jedoch auch zweiundzwanzig Würfel benötigt; ebenso enthält die erste Schicht auf Quadern mit den Maßen 5 x 3 x 1, 7 x 2 x 1 und 11 x 1 x 1 jeweils sechsundvierzig Würfel.
Wir definieren C(n) als die Anzahl der Quader, die n Würfel in einer ihrer Schichten enthalten. Also C(22) = 2, C(46) = 4, C(78) = 5, und C(118) = 8.
Es stellt sich heraus, dass 154 der kleinste Wert von n ist, für den C(n) = 10 ist.
Finde den kleinsten Wert von n, für den C(n) = 1000 ist.
--hints--
cuboidLayers() sollte 18522 zurückgeben.
assert.strictEqual(cuboidLayers(), 18522);
--seed--
--seed-contents--
function cuboidLayers() {
return true;
}
cuboidLayers();
--solutions--
// solution required